アプリケーションギャラリ

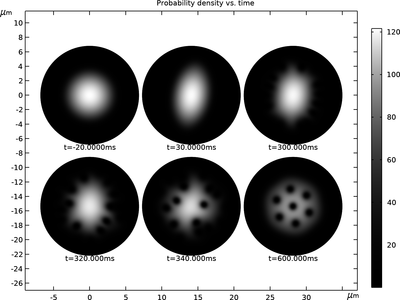
This tutorial model solves the Gross–Pitaevskii Equation for the vortex lattice formation in a rotating Bose–Einstein condensate bound by a harmonic trap. The equation is essentially a nonlinear single-particle Schrödinger Equation, with the inter-particle interaction represented by a potential energy contribution in proportional to the local particle density. The time evolution in rotating frame with phenomenological damping is configured with built-in features of the Schrödinger Equation physics interface. Nucleation of vortices is seen starting at the periphery of the condensate. Subsequently the system goes through a period of spectacular dynamical instability before settling down in the low energy state of a vortex lattice. The Optimization Module is used for parameter estimation from the numerical results. The time scales of the initial oscillation and the eventual collapse of the ellipticity parameter agree well between simulation and the experimental data published by Madison et al.