アプリケーションギャラリには電気, 構造, 音響, 流体, 熱および化学分野に関連する COMSOL Multiphysics® チュートリアルおよびデモアプリファイルが用意されています. これらの例はチュートリアルモデルまたはデモアプリファイルとそれに付随する手順をダウンロードすることにより独自のシミュレーション作業の開始点として使用できます.
クイック検索機能を使用して専門分野に関連するチュートリアルやアプリを検索します. MPHファイルをダウンロードするには, ログインするか, 有効な COMSOL ライセンスに関連付けられている COMSOL Access アカウントを作成します. ここで取り上げた例の多くは COMSOL Multiphysics® ソフトウェアに組み込まれ ファイルメニューから利用できるアプリケーションライブラリからもアクセスできることに注意してください.
This tutorial shows how to clean an imported CAD geometry using Geometry Cleanup. This helps to improve the mesh and reduce the total number of elements. 詳細を見る
This app demonstrates the following: Geometry parts and parameterized geometries Sending an email with a report when the computation is finished User-defined email server settings which is useful when running compiled standalone applications Options for setting different mesh sizes ... 詳細を見る
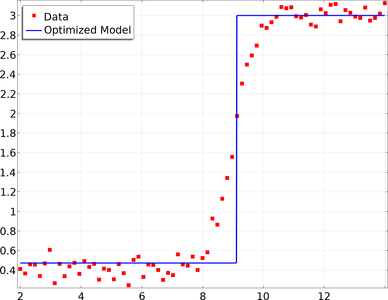
This app demonstrates the following: Importing measured data from a text file or use built-in functionality for data generation Automatically change solver options based on the input Dynamically update the equation display The app can be used to estimate parameters in models without ... 詳細を見る
This model simulates atmospheric galvanic corrosion of an aluminum alloy in contact with steel. The electrolyte film thickness depends on the relative humidity of the surrounding air and the salt load density of NaCl crystals on the metal surface. Empirical expressions for the oxygen ... 詳細を見る
この例では, 容器内に沈められた加熱チューブの配列と, その底部から流体が流入する様子について説明します. これは, 熱伝達と結合した流体力学を含むため, マルチフィジックスモデルです. 圧力と速度場はナビエ・ストークス方程式の解であり, 温度は熱方程式を通じて解かれます. このモデルでは, 方程式は両方向に結合されています. 流体を持ち上げる浮力は, 密度を通じて温度に依存する力項を介して圧縮性ナビエ・ストークス方程式に入力されます. 同時に, 熱方程式は対流熱伝達を考慮します. この実装では, ... 詳細を見る
Model of the sound radiation from a circular duct with uniform flow. The convected acoustic problem is described using the linearized potential flow equations, solved in the frequency domain. The acoustic inlet is treated including higher order modes using the Port boundary condition and ... 詳細を見る
The vibration modes of a thin or thick circular disc are well known, and it is possible to compute the corresponding eigenfrequencies to arbitrary precision from a series solution. The same is true for the acoustic modes of an air-filled cylinder with perfectly rigid walls. A more ... 詳細を見る
この研究では, コンピュータの電源ユニット (PSU) の熱挙動をシミュレートします. このような電子機器の筐体の多くには, 電子部品が過度の高温によって損傷するのを防ぐための冷却装置が備えられています. このモデルでは, 排気ファンと穴あきグリルによって筐体内に空気の流れが生じ, 内部の熱を冷却します. 詳細を見る
The Poroelasticity interface couples Darcy's law and solid mechanics to assess deformation of porous media that results from fluid withdrawals. The model builds on top of the Terzaghi Compaction example. Results from Terzaghi compaction and Biot poroelasticity analyses are compared to ... 詳細を見る
The Korteweg-de Vries (KdV) equation models water waves. It contrasts sharply to the Burgers equation, because it introduces no dissipation and the waves travel seemingly forever. Solitons have their primary practical application in optical fibers. Specifically, a fiber’s linear ... 詳細を見る