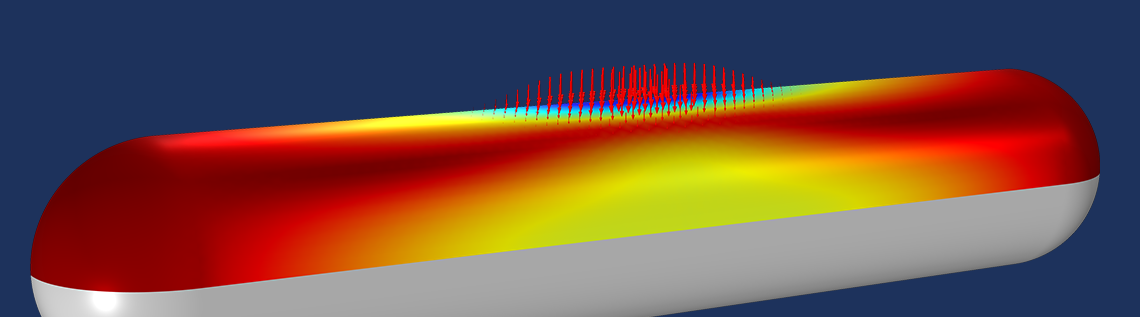
COMSOL Multiphysics® ソフトウェアには, 非線形問題を設定して求解する際に自動的に使用されるシンボリック微分エンジンが搭載されていることをご存知ですか? この機能は, このようなモデルを求解するときにソフトウェアの高いロバスト性を保証しますが, いくらかのコストが伴います. このブログでは, この機能をいくつかの異なる例で見て, その利点とトレードオフを検討してみましょう.
シンボリック微分による単純な非線形問題の求解
まず, 比較的簡単な1自由度の非線形問題である次のような陰方程式を見てみましょう.
Tは系の集中温度, Qは熱負荷, そして上式の分母(1+T^2/100)は系の熱コンダクタンスを表していると言えます.
パラメーターQのさまざまな値を解くことが目的です. このような非線形問題の解は, 減衰ニュートン法によって求めることができます. COMSOL Multiphysics® では, 以下の残差を書き出し,
それをグローバル方程式インターフェースに入力することでこれを行います(以下のスクリーンショットを参照).
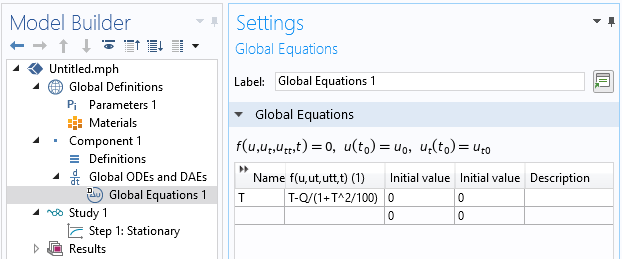
非線形方程式を解くために使用されるグローバル方程式インターフェース.
この式を(変数)の値の範囲で解き Q, その解をプロットすると, 以下のようになります.
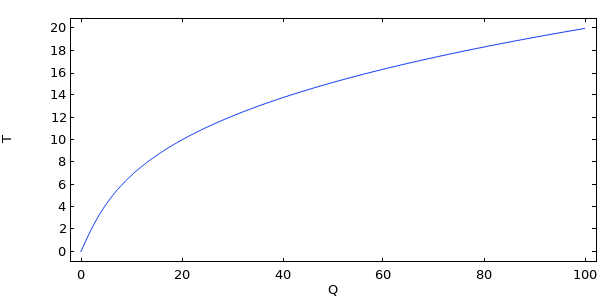
1自由度の非線形問題の解.
説明のために, Qの値の範囲とTの値の選択について, 残差をプロットしてみましょう. ゼロ交差の点は, 上のプロットの解です.
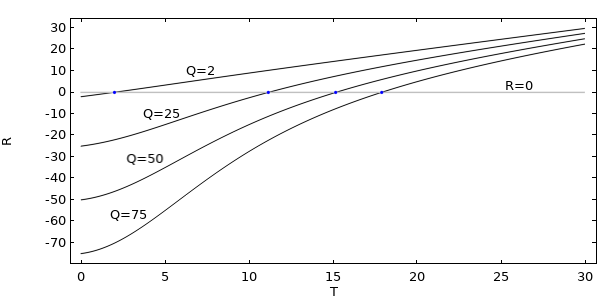
パラメーターQの異なる値の残差をプロットしたもの. ゼロ交差からのTの値が, 非線形方程式の解となります.
また, 同じ範囲のTとQの値に対する残差の対応する微分(ヤコビアン)を以下にプロットしてみましょう.
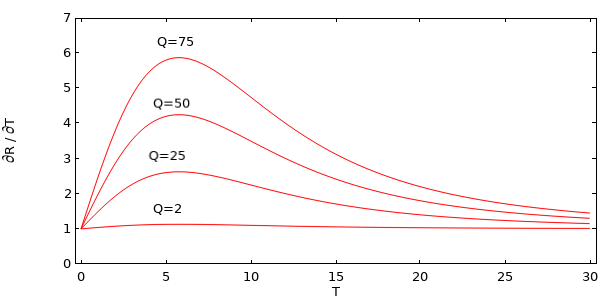
異なる値のQに対する残差の微分のプロット.
Qの値が大きくなるにつれて, ヤコビアンはより非線形な関数になっていることがわかります. また, (この単純なケースでは)微分をマニュアルで書き出すこともできます.
ソフトウェアは自動的にこの微分をシンボリック微分で行い, ニュートンのステップで使用することを覚えておいてください.
さて, この式を少々複雑にしているのは, 残差の後半部分の分母です(先ほどご説明したように, この項はシステムの熱抵抗と考えられます). しかし, 実は, 分母の項
R(T) =(T – Q/nojac(1+T^2/100))
をnojac()演算子でラップして, 以下のスクリーンショットのようにグローバル方程式を修正することで, この項を無視することができるのです.
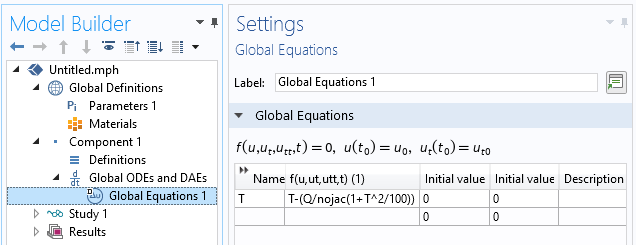
nojac()演算子の使用方法を示すスクリーンショット.
その結果, nojac()算子内のすべてのものは, シンボリック微分エンジンによって無視されます. つまり, この演算子内の項はヤコビアンへの寄与はありません. Tに対する残差の微分は, 単純に以下のようになります.
この簡略化された導関数は,Qの値が低い場合には良い近似値でしかなく, ソルバーがQのすべての値に対して解に収束しないという効果があることが, 検証によってわかります. そのため, 一部の項の導関数を取得する(この場合は非常に小さい)オーバーヘッドを避けることで, 問題を少しだけ単純化しましたが, 場合によっては求解できなくなってしまいました.
COMSOL Multiphysics® におけるnojac()演算子の使用法
nojac()演算子の他の使い方もいくつか見てみましょう.
グローバル方程式を次のように
R(T) = nojac(T – Q/(1+T^2/100))
と書いたとすれば, 微分は正確にゼロとなり, この問題は全く解けないので, このケースは興味深くありません.
また, 1つの項だけにnojac()を適用してみましょう.
R(T) = T – Q/(1+nojac(T)*T/100)
そうすると, 微分は次のようになります.
これは正確な残差に非常に近く, 少なくともこのケースでは, ヤコビアンをこのように近似しても, Qのすべての値に対してソルバーは収束します. 計算コストは下がっていませんが, ここで注目すべき点は, 残差の項の任意の部分にnojac()演算子を適用できることです.
さて, これまでに学んだことを復習してみましょう.
nojac()演算子を使用して, ヤコビアンへの寄与から項を省略することが可能- 項を省略すると, 非線形ソルバーの収束に影響する
- 項を省略することで, 計算モデルのサイズを縮小することが可能
ただし, 最後の点は, この小さな例ではそれほど明白ではありません.
大型非線形モデルのサイズ縮小
次に, 3次元のより大きなモデルを見てみましょう. 1cm角の立方体で熱伝導の問題を解き, この部分に非常に細かいメッシュを適用することで, 約300万の自由度を持つ大きなモデルができあがります.
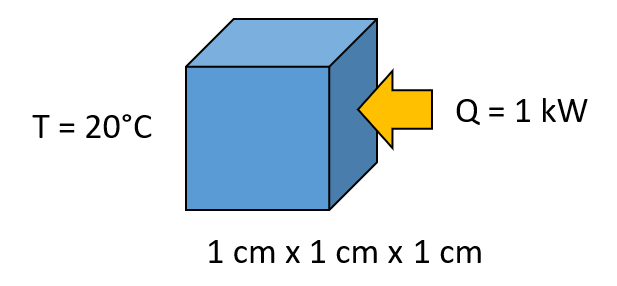
非常に細かいメッシュで解析するための単純な熱伝導問題の模式図.
また, 材料特性を温度の関数とし, すでに見たものと同様の材料特性を使用して, ユーザー定義の式で材料の熱伝導率を定義します.
(
(1+(T[1/K])^2/100)[W/m/K]
これは, 以下のスクリーンショットで示されているように, フィジックスインターフェース内で直接行われます.
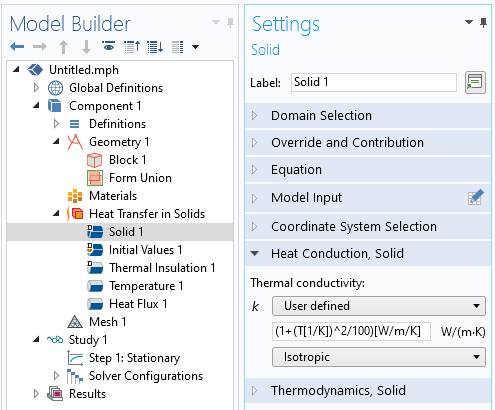
温度の関数としてマニュアルで定義された熱伝導率.
デフォルトの設定でこの問題を解く場合, モデルを求解するには, 減衰ニュートン法を4回繰り返す必要があり, 標準的なデスクトップコンピュータでは,約135秒, 12GB強のメモリを使用することになります. また, 求解プロセスの途中で, ログに次のようなメッセージが表示されます.
非対称な行列が見つかりました.
このメッセージは, 材料特性に温度依存項があることに起因します. つまり, 材料特性の非線形項はヤコビ行列を非対称にし, その結果, モデルを解くのに多くのメモリを必要とします. それでは, 材料特性の式全体をnojac()演算子でラップしてみましょう.
nojac(1+(T[1/K])^2/100)[W/m/K]
モデルを再実行すると, モデルは収束し, 求解には約10GBを要しますが, デフォルトの減衰ニュートン法では5回の反復が必要になることがわかります. つまり, 必要なメモリ容量は減りましたが, 収束までの反復回数は増えているということです. 最も興味深いことに, 求解時間は125秒で, 以前よりも少し短くなっています. これはなぜでしょうか? ソルバーは収束までに多くの反復を必要としますが,ヤコビアン行列が対称的であり,処理する必要のあるデータが少ないため,各反復にかかる時間は短くなるのです.
つまり, この場合, nojac()演算子を使用することで, 解に収束するまでに必要な反復回数が増えるにもかかわらず, 求解時間と必要なメモリの両方を削減することができます. また, 更新された材料特性式を使用して材料特性自体が正しく評価されているため, 同じ解に収束することにもご注目ください.
非局所カップリング項の回避
最後に, もう1つの例として, 下図のような圧縮性のある気体が入った薄肉の容器を押しつぶす場合を見てみましょう. これは, 構造力学モジュール内で利用可能なシェル定式化を使用してモデル化できます.
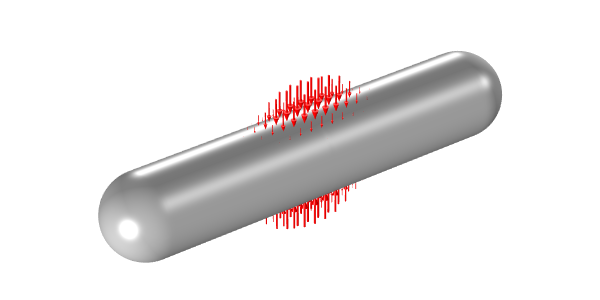
外部破砕荷重が加えられた圧縮性ガスを含む薄肉タンク.
対称性を利用することで, モデルをフルモデルの1/8にまで縮小することができます. まず, 破砕を近似した分布荷重と, 内部の圧縮性ガスを表す圧力荷重をかけます. 圧縮性ガスを表現するために, 空気を充填した超弾性シールの圧縮の例と同じように, 変形した容器の体積を計算するアプローチを使用します. つまり, 積分カップリング演算子を使って, タンクの表面全体に均一な圧力負荷をかけ, その圧力をタンク全体の変形に基づいて計算するのです.
この非局所的カップリングの影響で, タンクの各部の変形が圧力に影響を与え, 圧力が各部の変形に影響を与えるため, ヤコビ行列が非常に密になります. このモデルをデフォルトの非常に細かいメッシュ設定で解いた場合, 約22,000自由度のモデルを解くのに約12GBのメモリと400秒の時間を要しました.
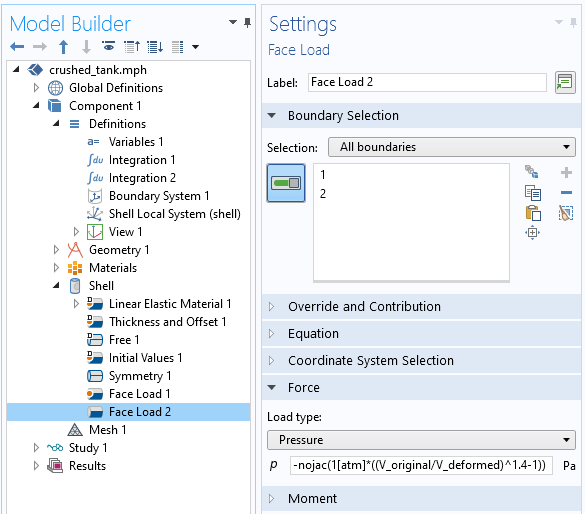
破砕されたタンクのモデル内の変更された圧力を示すスクリーンショット.
しかし, 適応された圧力をnojac()演算子でラップするだけで, 非局所的カップリングが省略され, 必要なメモリと解答時間が短縮されました. この方法では, 同じ解に収束するのに必要なメモリは3GB, 時間は10秒だけです.
最後に
デフォルトでは, ソフトウェアは常に正確なヤコビアンを取るようになっています. これにより, 収束の可能性が最も高くなるからです. 一般的には, 可能な限りロバストな解を取得するために, 時間とメモリをいくらか犠牲にします. しかし, ヤコビアン行列から選択した項を省略する機能と柔軟性があることがわかりました. この機能を使用するには, 材料特性を明示的に変更するか, 基本的な支配方程式を変更するか, モデル内に独自の変数式を記述する必要があるため, これは少し高度なユーザー機能となります.
もちろん, この機能を使うとヤコビアンが近似され, 収束が遅くなったり, 収束しなくなったりすることがありますので, そのような場合には使用しないでください. しかし, nojac()演算子を使用してもモデルが収束する場合は, 完全なヤコビアン評価を行った場合と同じ解に収束し, 時間やメモリの使用量も少なくて済みますので, 複雑なマルチフィジックスモデルを構築する際に知っておくと便利な機能です.


コメント (0)