射影演算子を使用してシミュレーション結果を分析する

壁に手を使って影絵を作ったことがありますか? (3次元の) 手の後ろに光を当てると, 壁に2次元の射影が作成されます. COMSOL Multiphysics でシミュレーションデータを分析する場合, 射影演算子 を使用してモデルで同様の操作を行うことができます.

2D軸対称パイプ流れモデルの例

流れによって運ばれる化学種 c を含む 2D 軸対称パイプ流れモデルの解を計算したとします. パイプ内の濃度の空間分布を見ると, 濃度が流れの方向に減少していることに気付きます. この傾向は, 以下の表面プロットで定性的に明確に確認できますが, より定量的に表現したい場合があります.

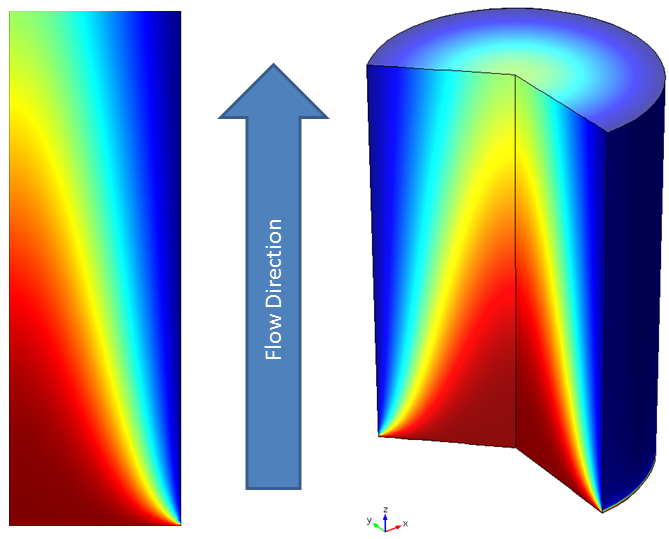
濃度と流れの方向.

これを実現する1つの方法は, パイプの軸に沿ったすべての断面の平均濃度をプロットすることです. COMSOL Multiphysics では, 射影演算子 を使用してこれを行います.

射影演算子はソース次元を1つ減らす

シャドウグラフィーのアナロジー をもう一度見直し, 概念的にそれがどのように機能するかを考えてみましょう. 光源と壁の間に手を置くと, 手が光路を遮り, 壁に影, つまり3Dの手の2D画像が見えます.

COMSOL ソフトウェアの射影演算子は, モデルの “影絵” を作成するツールと考えることができます. モデル (またはその一部) が手の役割を担います. これは, 演算子設定で ソース と呼ばれます. このアナロジーの壁は, モデルの別の部分, 行先 です. 影が形成されるのはここです.

COMSOL Multiphysics での射影の結果は, 影絵のように, ソースの次元を1つ減らします. “像” は, “光の方向” で式を積分することによって形成されます. この方向は, ソースと行先の間のマップによって指定されます. ここでは, 線形マップ用の線形射影と, より複雑な状況用の一般射影の2つの選択肢があります. これらを使用して, 上で紹介したパイプの軸に沿った平均断面濃度をプロットしてみましょう.

線形射影

流路の軸に沿った高さ z の断面における平均種濃度 c_{av}(z) に関心があるとします. 2D軸対称ジオメトリであるため, 断面は水平線で表され, 平均は次の積分で計算できます.

ここで, A(z)=\pi\cdot R(z)^2 は断面積, R(z) は積分の長さで, この例ではパイプの半径に等しくなります.

COMSOL ソフトウェアでは, ここに示す線積分は線形射影演算子で解くことができます. 上記の説明から, 演算子を設定するには, ソース, 行先, および2つの間のマップが必要であることがわかります. コンポーネントの定義に線形射影を追加するときは, まずソースに属するジオメトリエンティティを選択します.

パイプの例では, これはモデルドメイン 1 全体です. 線形射影では, 選択した頂点間の線で定義される線形マップを使用します. これで, マップを設定する準備が整いました. まず, 行先から始めます. ここでは, これが流路の軸になるはずなので, それに応じて行先の頂点 1 と 2 を選択します. 次に, 行先に対応するソース内の線を選択します. このシナリオでは, それは同じ線なので, ソースの頂点 1 と 2 に同じポイントを割り当てます. ソースには, 行先よりも1つ多くの頂点があります. これは, 線積分の方向を指定するために使用されます. 例では, ここで頂点 3 を選択します. つまり, 線積分は, 下の図の白い矢印で示されているように, この線と平行に計算されます.

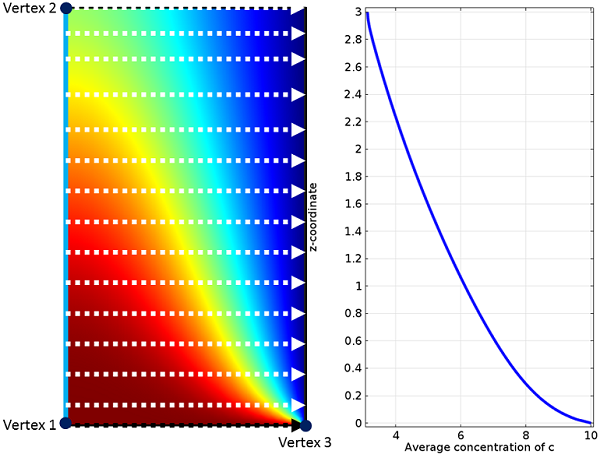
線積分とその結果得られる化学種の平均濃度 c を表す矢印が付いた濃度.

まとめると, 最初の軸 (頂点 1 と 2 の間) には線積分の開始点が含まれ, 2番目の軸 (頂点 1 と 3 の間) には積分の方向が示されます.

これで, 演算子 (デフォルトでは “linproj1” と呼ばれます) を使用して c の濃度を積分し, それを積分の長さで割って平均濃度を取得できます. 長さ R(z) が定数でないか不明な場合は, 演算子によって評価することもできます. 結果の方程式は次のとおりです:

結果をプロットするには, linproj1(c*2*pi*r)/linproj1(2*pi*r) を式として1D折れ線グラフを使用し, 左の境界を選択範囲として選択します.

一般射影

一般射影演算子を使用して平均を設定することもできます. 名前が示すように, この演算子はより複雑なマップを処理でき, たとえば, ドメインの任意の (曲線) 方向で経路積分を使用できます. もちろん, 一般射影演算子を使用して線形射影を設定することもできます. このオプションは, 線形射影演算子を適切に設定するための頂点がモデルジオメトリにない場合に関係します. この状況では, ジオメトリを変更して必要な頂点を含めるか, 一般射影演算子を使用して, 数式を使用してソースと行先間のマップを直接定義することができます.

理解を深めるために, 2D軸対称のサンプルモデルをもう一度見てみましょう. コンポーネントの定義セクションに一般射影を追加した後, 最初にソースジオメトリを選択します. 演算子の設定には, ソースマップと行先 マップを定義する数式のフィールドが含まれています. この例では, 式は座標の線形関数です. 再び行先から開始する場合は, このジオメトリに流れ軸, つまり z 軸を入力します. ソースで同じ線を使用するため, x 式には z 軸もあります. y 式は積分の方向を定義します. この場合は r 軸です. これで, 一般射影演算子 (デフォルトでは “genproj1” と呼ばれます) を使用して, 以前の線形射影と同じ結果を得ることができます.

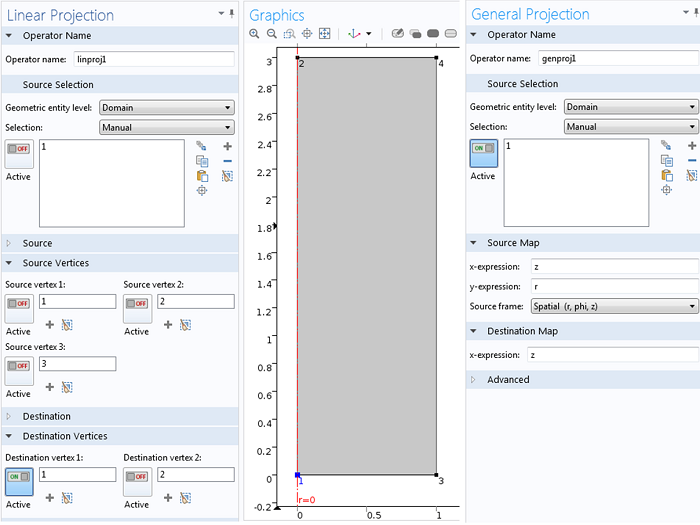
線形および一般射影演算子の設定.

複数の次元の射影

非対称の濃度分布が原因で, モデルの3Dバージョンがある場合はどうすればよいですか?この場合, 次の x と y の二重積分を計算することで, 各 xy 断面の平均を計算できます.

ここで, A(z) は断面積です.

COMSOL Multiphysics では, 2つの射影結合演算子を使用してこの二重積分を評価できます. 最初の演算子は, x の積分によって3Dから2Dに射影します (y 方向もここでは同様に機能します). 2番目の演算子は, 残りの座標を積分することによって, 最初の演算子の結果を2Dから1Dに射影します.

ジオメトリに yz 平面の平面が含まれている場合, 演算子を設定するのが最も簡単です. そうでない場合は, 少なくとも3つのオプションがあります. コンポーネントのジオメトリを変更できますが, 解を再計算する必要があります. これは, モデルの計算に時間がかかる場合には便利なオプションではありません. 代わりに, 一般射影演算子を使用できます. または, 平面の2Dジオメトリを持つ別のコンポーネントを追加し, 3Dコンポーネントから2Dコンポーネントに射影することもできます. これは, 最も簡単なオプションです. これは, ソースと行先が同じモデルコンポーネントに属している必要がないため機能します. 3番目のオプションを選択した場合は, 解を更新して, すべてを再計算する必要がなくなります.

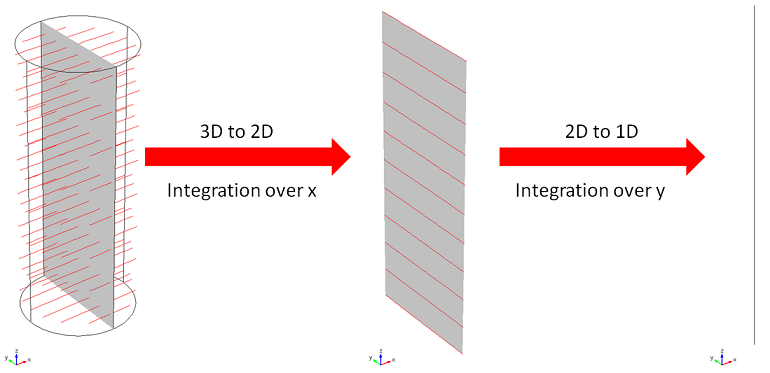
二重積分は2つの射影演算子によって実行されます. 赤い線は積分された線を表します.

結論

ここでは, 射影演算子を使用してシミュレーションデータを分析する方法を示しました. 適用可能な場合, この手法は結果の本質を抽出し, 基礎となる物理現象をより深く理解するのに役立ちます. 射影演算子の使用についてさらに詳しく知りたい場合は, お問い合わせ ください.