Menu
COMSOL ブログ

シミュレーションによる光計算装置の解析

Author Image

Xinzhong (Tom) Chen 著

2022年 8月 11日

光コンピューティングは, 現在の電子コンピュータに代わるパラダイムです. このブログでは, 光コンピューティングの概念を探求し, 光行列乗算ネットワークがどのように機能するかを説明します. また, COMSOL Multiphysics® ソフトウェアと波動光学モジュールアドオン製品を使用して光計算デバイスをモデル化する方法についても説明します. これらの製品を組み合わせて使用すると, 光学的に大規模なシステムをシミュレーションするときにビームエンベロープ法を適用する利点がわかります.

光コンピューティング入門

ムーアの法則

過去数十年にわたり, コンピュータの機能は飛躍的に向上しました. この増加はムーアの法則に従っています. 集積回路内のトランジスタは 2 年ごとに 2 倍になる一方, コンピューターのコストは低下します. これにより, 私たちが今日享受している最新技術の大部分が可能になります. たとえば, 主流のコンピューターチップはトランジスターなどの電子部品のみをベースにしており, チップあたりのトランジスターの数は ほぼ 2 年ごとに 2 倍になり続けています. この増加に対応し, 管理可能な電力効率でコンピューターチップのパフォーマンスを向上させるには, トランジスターを含むチップ上の電子部品の小型化が重要かつ避けられません. 技術者らはトランジスターを cm サイズから nm サイズに縮小することでこの点で目覚ましい仕事をしてきましたが, 最終的には根本的な限界がそのようなデバイスの進歩を妨げることを認識することが重要です. たとえば, 電子部品のサイズが原子レベルに近づくと, 量子効果により機能が不安定になります. 科学および工学コミュニティは, 電子コンピューターに代わるパラダイムを長い間検討してきました. 最近大きな注目を集めているオプションのひとつは, 光コンピューティングです. これは, 電流 (電子) の代わりに光 (光子) を使用して計算を実行します.

光コンピューティングは新興技術ですが, 光はかなり以前から情報技術, 特に情報伝達のために使用されてきました. 損失が極めて低い光ファイバーは, 光の速さで長距離に情報を運ぶことができます. 光ファイバーネットワークデバイスは, データセンターだけでなく一般家庭でも使用されています. ただし, 計算に光を使用することは, 商業化の点ではまだ初期段階にあります.

光学における数学計算

特定の光学プロセスが数学計算に対応していることはよく知られています. 例として, 光の回折を考えてみましょう. 光が回折媒体を通過すると, 本質的にフーリエ変換積分が実行されます (この概念については, 今後のブログで詳しく説明します). ただし, 光学系が今日のコンピューターのような汎用数学計算を実行できるかどうかは, すぐには明らかではないかもしれません. 現在, 光コンピューティングにはさまざまな種類があります. さまざまなメカニズムを使用して, 単純な算術, 行列の乗算, 積分と微分などを実行できることが証明されています. 一般に, アナログ計算は, 特別に設計された系における光の回折, 散乱, または伝播で発生する可能性があります.

MZI モデルでシミュレートされた磁場分布を示す画像.
集積MZI ネットワークモデル.

左: 自由空間マッハツェンダー干渉計 (MZI) における磁場分布のシミュレーション. 右: 集積 MZI ネットワーク.

一般的な光コンピューティングについて説明するのではなく, 1 つの特定のアナログ光計算システム, つまりマッハツェンダー干渉計 (MZI) ネットワークに基づく行列乗算デバイスについて詳しく説明します. 実際の問題を解決するには, 多くの電力消費を必要としない方法で行列乗算を迅速に実行することが望ましいため, このシステムは非常に興味深く便利です. これには, 機械学習に関連する問題が含まれます. ディープニューラルネットワークなどの最新の機械学習アルゴリズムの大部分は, 大量の行列乗算に依存しています. 高速な行列乗算を実行する光学システムを構築できれば, 機械学習の力を最大限に活用できます.

光行列乗算

マッハツェンダー干渉計

まず, 2 つの入力と 2 つの出力を持つ単一の MZI が 2 行 2 列のユニタリ行列乗算をどのように実行するかを理解する必要があります. 以下の図に示すように, 2 つの 50:50 ビームスプリッター (BS) と 3 つの位相シフターで構成される古典的な MZI 構成から始めます. 光が位相シフターを通過すると, \theta, \alpha, および \beta によって位相がシフトします. 入力ビームの複素振幅を E_1 と E_2 とラベル付けします. 出力ビームの振幅を E’_1 および E’_2 としてラベル付けします.

次に, E’=U^2(\theta,\alpha,\beta)E を示します. ここで

E= \begin{bmatrix}E_1 \\E_2\end{bmatrix},
E’= \begin{bmatrix}E’_1 \\E’_2\end{bmatrix}

U^2(\theta, \alpha, \beta) は\theta, \alpha, \beta で制御される任意のユニタリ行列です. 上付き文字 (この場合は 2) は行列の次元を示します. このブログ全体を通じて, この表記規則に従います. \theta, \alpha, および \beta を制御することで, 次のことができます. つまり, この光学系は, ユニタリ 2 行 2 列の行列乗算を光の速度で実行します.

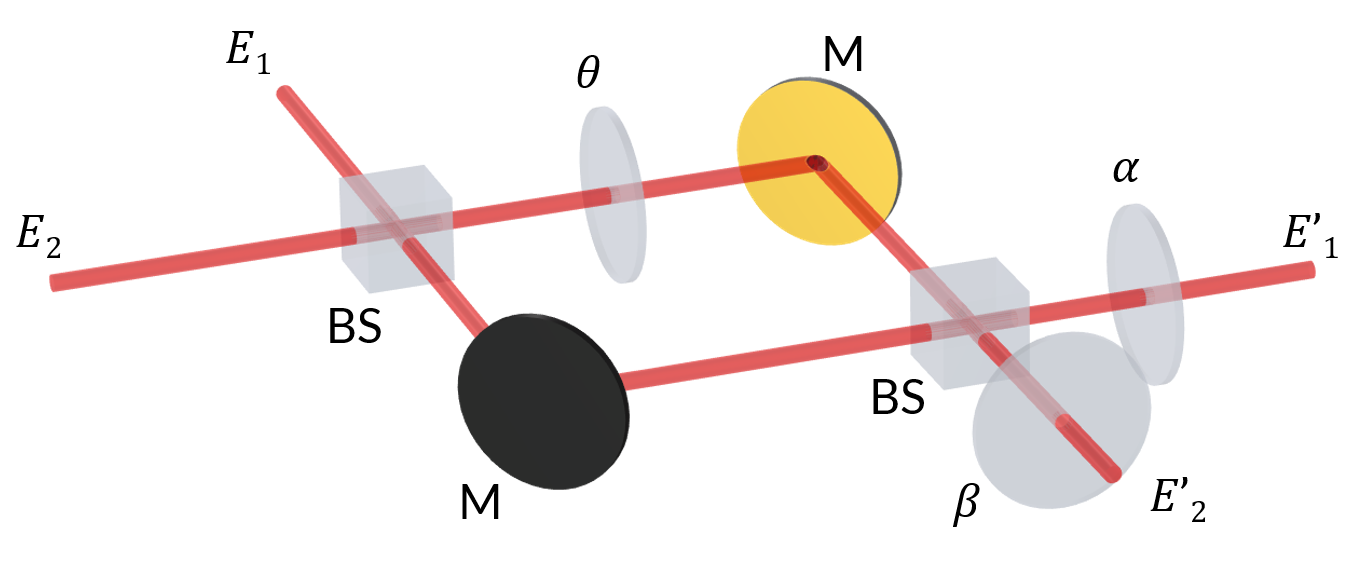
2つのビームスプリッターと3つの位相シフターを備えた MZI の概略図.
2つの 50:50 ビームスプリッターと, 光の位相を \theta, \alpha, \beta だけシフトする3つの位相シフターを備えた古典的な MZI . Ｍは反射ミラーを示す.

ビーム E_1 が対称 50:50 ビームスプリッターを通過すると, 送信ビームは \frac{\sqrt{2}}{2} E_1, 反射ビームは -j\frac{\sqrt{2}}{2}E_1 になります. 反射ビームに虚数 -j が現れるのは, e^{-j\pi/2}=-j であるので, 反射の \pi/2 位相シフトによるものです. たとえば最初のビームスプリッターを通過する光の場合, 位相係数 e^{-j\theta} が検出されます. これまで説明してきた情報を考慮すると, 通過する光を合計することで, さまざまなパスを介して E’_1 と E’_2 を書くことができます:

E’_1=j\frac{\sqrt{2}}{2}(-j\frac{\sqrt{2}}{2}E_1+\frac{\sqrt{2}}{2}E_2)e^{-j\theta}e^{-j\alpha}-\frac{\sqrt{2}}{2}(\frac{\sqrt{2}}{2}E_1-j\frac{\sqrt{2}}{2}E_2)e^{-j\alpha},
E’_2=-\frac{\sqrt{2}}{2}(-j\frac{\sqrt{2}}{2}E_1+\frac{\sqrt{2}}{2}E_2)e^{-j\theta}e^{-j\beta}+j\frac{\sqrt{2}}{2}(\frac{\sqrt{2}}{2}E_1-j\frac{\sqrt{2}}{2}E_2)e^{-j\beta}

いくらかの代数計算をして

E’_1=\frac{e^{-j\alpha}}{2}[(e^{-j\theta}-1)E_1+j(1+e^{-j\theta})E_2],
E’_2=\frac{e^{-j\beta}}{2}[j(1+e^{-j\theta})E_1+(1-e^{-j\theta})E_2]

を得ます.

行列形式で

\begin{bmatrix}E’_1\\E’_2\end{bmatrix}=\frac{1}{2} \begin{bmatrix}e^{-j\alpha}(e^{-j\theta}-1) & je^{-j\alpha}(1+e^{-j\theta})\\je^{-j\beta}(1+e^{-j\theta}) & e^{-j\beta}(1-e^{-j\theta})\end{bmatrix} \begin{bmatrix}E_1\\E_2\end{bmatrix}

が得られます.

この行列

U^2(\theta,\alpha,\beta)=\begin{bmatrix}e^{-j\alpha}(e^{-j\theta}-1) & je^{-j\alpha}(1+e^{-j\theta})\\je^{-j\beta}(1+e^{-j\theta}) & e^{-j\beta}(1-e^{-j\theta})\end{bmatrix}

が2×2一般複素ユニタリ行列の形をしていることが分かります. U^2U^{2*}=I であることは簡単に分かります. ここで I は単位行列です. 幾何学的に言えば, この行列は入力ベクトルの回転として解釈できます. さて, COMSOL Multiphysics® でこのような光学系をどのようにモデル化できるでしょうか?

波動光学モジュールを使用してモデリングを行う理由はいくつかあります. 一見すると, 系のサイズが波長よりも桁違いに大きいため, 光線光学モジュールも適しているように思えるかもしれません. ただし, MZI については, 主に干渉効果に関心があります. 光線光学シミュレーションは通常, 干渉を自動的に考慮しないため, 理想的なアプローチではありません.

波動光学モジュールを使用すると, 干渉は自動的に考慮されます. また, このモジュールを使用して, このサイズのモデルの処理に適した電磁波 (ビームエンベロープ)インターフェースを実装できるようにしてみます. ビームエンベロープ法は, 別のブログ で説明されているように, 長距離ビーム伝播問題のシミュレーションに特に適しています. ゆっくりと変化する包絡線関数と急速に変化する位相関数の積として場を分離することで, 包絡線関数の変化の速さに応じてモデルをメッシュ化するだけで済みます. これにより, ビームはほとんどの時間, 包絡線関数に変化がなく自由空間を伝播するため, 上図に示す MZI など, 多くの場合に多くの計算リソースが節約されます. この系には, 水平と垂直の2 つのビーム伝播方向があります. ビームエンベロープ法の双方向定式化は完璧な選択です. 次の設定で波数ベクトルを設定します:

  • 第1波:
    • x = ewbe.k
    • y = 0
  • 第2波:
    • x = 0
    • y = -ewbe.k

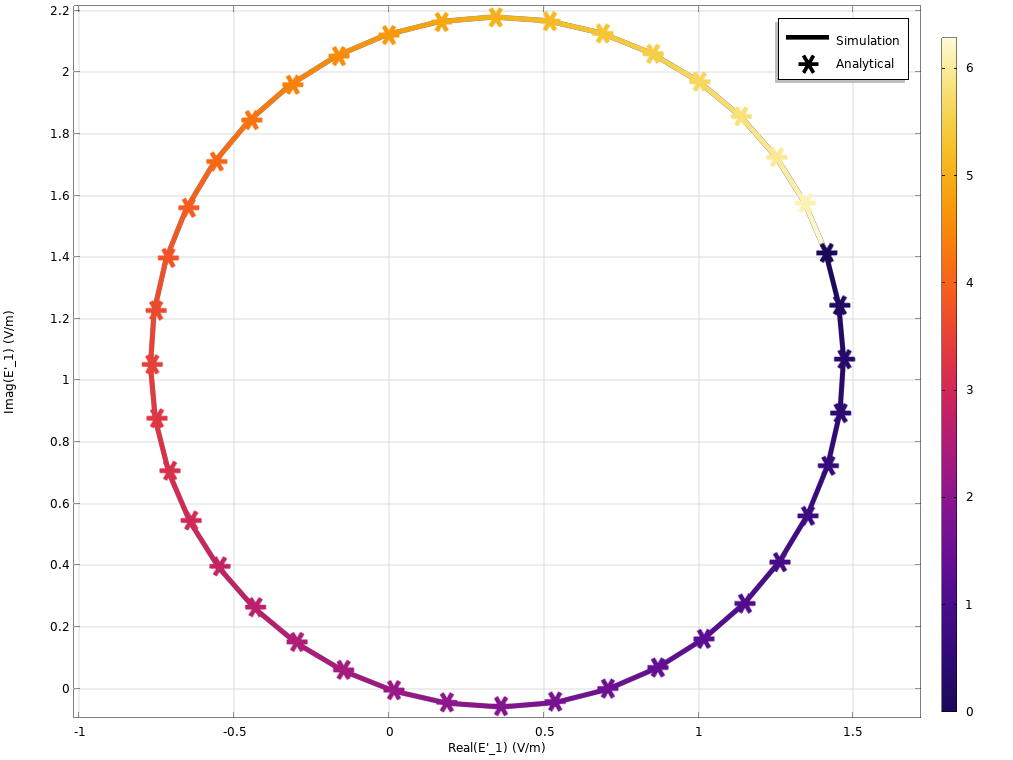
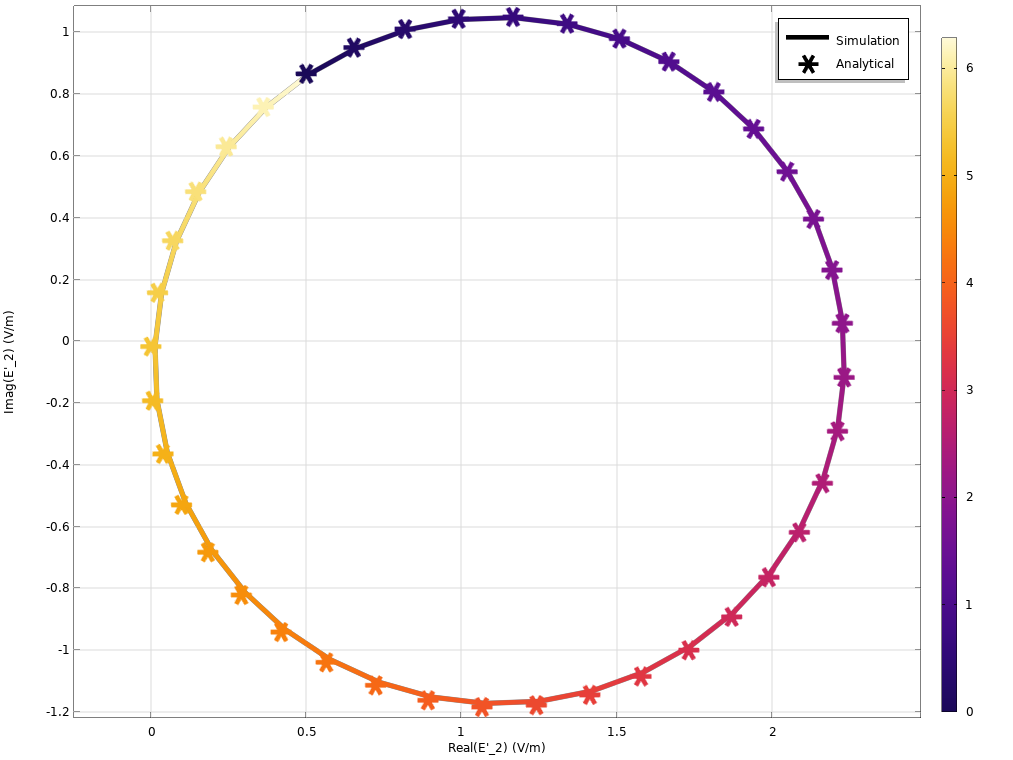
\alpha と \beta を固定し, \theta を徐々に変化させた場合, 0 から 2\pi まで, 出力場振幅 E’_1 と E’_2 を調べることができます. これは, 出力境界で ewbe.Ez を評価することによって行われます. 次に, 以下の図に示すように, E’_1 と E’_2 を複素平面にプロットします. \theta が変化すると, パスは閉じたループをたどります. これは, 以前に示した導出から予想されます. 図内のアスタリスクは, 前述の行列方程式を使用して計算されており, 予想どおり, 出力の ewbe.Ez と一致しています.

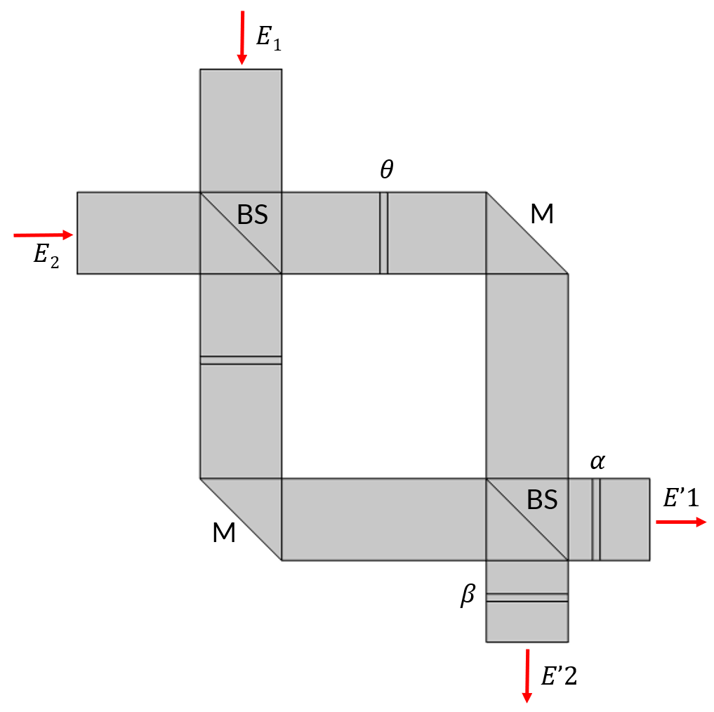
2D でモデル化された2つのビームスプリッターと3つの位相シフターを備えた MZI.

 

​

左: 2 つの 50:50 ビームスプリッター (BS) と, 光の位相を \theta, \alpha と \beta だけシフトする3つの位相シフターを備えた古典的な MZI の 2D モデル. Ｍは反射ミラーを示す. 右: \theta が 0 から 2\pi に変化したときの計算された場の分布. 入力振幅は E_1=1V/m および E_2=2V/m .

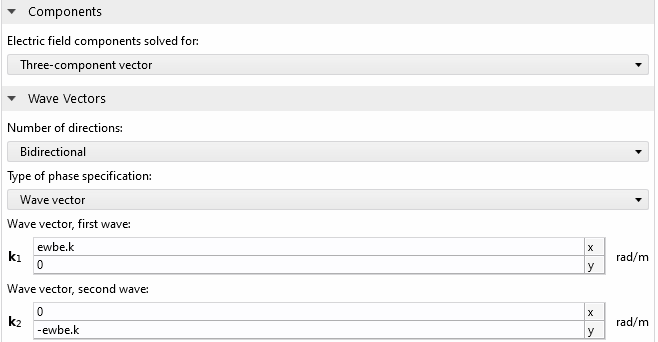
コンポーネントセクションと波動ベクトルセクションが展開された, 電磁波 (ビームエンベロープ) インターフェースの設定のスクリーンショット.
電磁波 (ビームエンベロープ) の設定.

\theta が0から2\piまで変化したときの複素 E'_1.
\theta が0から2\piまで変化したときの複素 E'_2.

\theta が 0 から 2\piに変化したときの複素 E’_1 (左のプロット) と E’_2 (右のプロット) . 実線はシミュレーション結果を表し, 星印は前述の解析的に導出された期待値. 横軸と縦軸はそれぞれ実数部と虚数部で, 色は \theta の変化.

nxn ユニタリ行列乗算

2 行 2 列のユニタリ行列の乗算を実現する方法がわかったのは有益ですが, ほとんどの場合, 次元がはるかに大きい行列を扱うことになることに注意することが重要です. ここで, MZI のネットワークを使用して任意の n 行 n 列のユニタリ行列の乗算を実行する方法を見てみましょう. ここで, 任意の n 行 n 列のユニタリ行列は2×2の \frac{n(n-1)}{2} 部分行列の積として記述できるという定理を適用します. たとえば, 4 行 4 列のユニタリ行列 U^4 は, U^4=R_{31}R_{32} R_{33}R_{21}R_{22}R_{11} と書くことができます. ここで

R_{11} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & U^2_1 \end{bmatrix}
R_{22} = \begin{bmatrix} 1 & 0 & 0\\ 0 & U^2_2 & 0\\ 0 & 0 & 1 \end{bmatrix}
R_{21} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & U^2_3 \end{bmatrix}
R_{33} = \begin{bmatrix} U^2_4 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}
R_{32} = \begin{bmatrix} 1 & 0 & 0\\ 0 & U^2_5 & 0\\ 0 & 0 & 1 \end{bmatrix}
R_{31} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & U^2_6 \end{bmatrix}

ここで, U^2_i は, 前述したように, 3 つの位相シフトを持つ 1 つの MZI によって制御される 2 行 2 列のユニタリ行列です. この行列分解は, n 次元ベクトル空間での一般的な回転を低次元での一連の回転とみなすことで直観的に理解できます. 物理的には, 各 MZI が R_{ij} を表す特定の順序で MZI のネットワークを構築できることを意味します. したがって, 系全体は, 光が通過するときに入力に対して任意の n 行 n 列のユニタリ行列乗算を実行します. 4 行 4 列のユニタリ行列の場合, 合計6つの MZI が必要です.

MZI 上の2行2列のユニタリ行列乗算コアの回路図 (電極にラベルが付けられている).

 

​

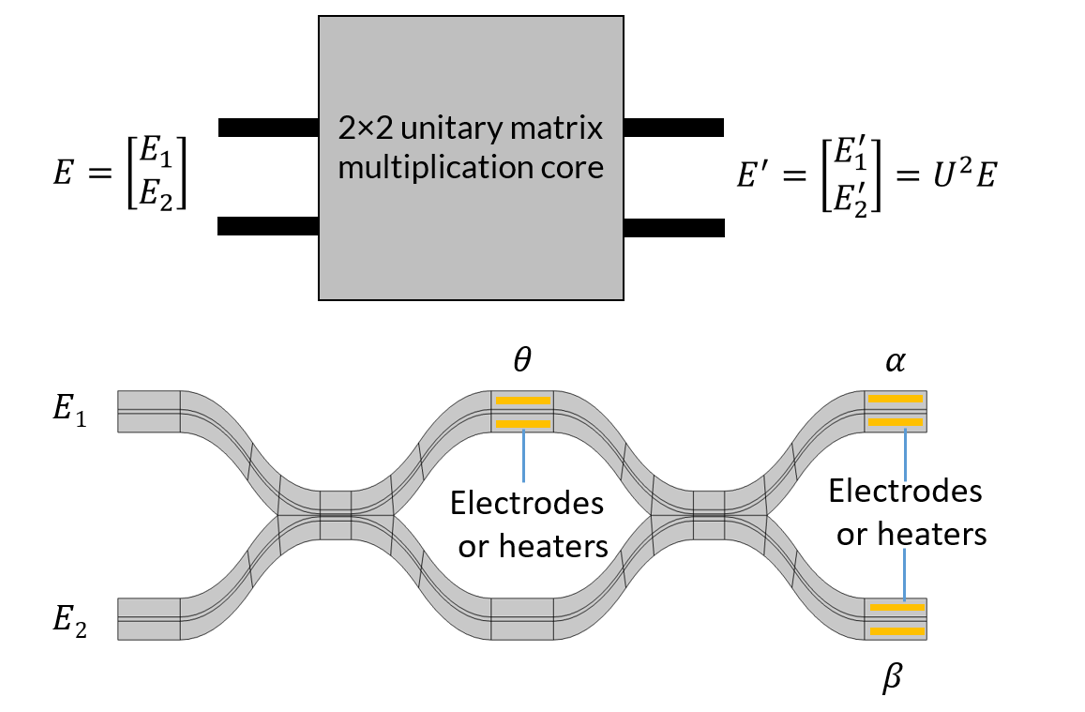
MZI は, 光2行2列のユニタリ行列乗算コアに相当します. 入力ベクトル E に対して2行2列のユニタリ行列の乗算を実行します. 行列 U^2 は, 電気光学効果または熱光学効果のいずれかを使用して, 印加電圧によって MZI に位相シフトを誘発することによってプログラムできます. 右のプロットでは, MZI の最初の移相器が継続的に調整され, 出力にベクトル回転が引き起こされます.

原理的には, この系は, 上図に示した古典的な MZI のような自由空間光学系を使用して実現できます. ただし, 自由空間光学系のスケーラビリティはかなり劣ります. ビームスプリッターとミラーはかさばるため, 持ち運びが困難です. 多数の部品を含む光ネットワークを構築したい場合は, よりスケーラブルな方法が必要です. 現在の相補型金属酸化膜半導体 (CMOS) 製造プラットフォームに基づく集積シリコンフォトニクスは, 高度に小型化された光学部品の大量生産に適した有望な候補です. 自由空間 MZI と同様に, 導波路結合器に基づく統合型 MZI は, 同じ光学機能を提供しますが, 4 桁も小型になります. これにより, 光学チップの設計が可能になります. ビーム 50:50 の分割と十分な位相シフトを備えた MZI を設計するには, ジオメトリの調整と最適化が必要です. ここでは詳しく説明しませんが, 電気光学効果を位相シフトメカニズムとして使用して導波路 MZI を設計する方法については, このブログを参考にしてください.

同様に, 屈折率の変調, つまり位相シフトを引き起こすことができる熱光学効果も一般的に利用されます.

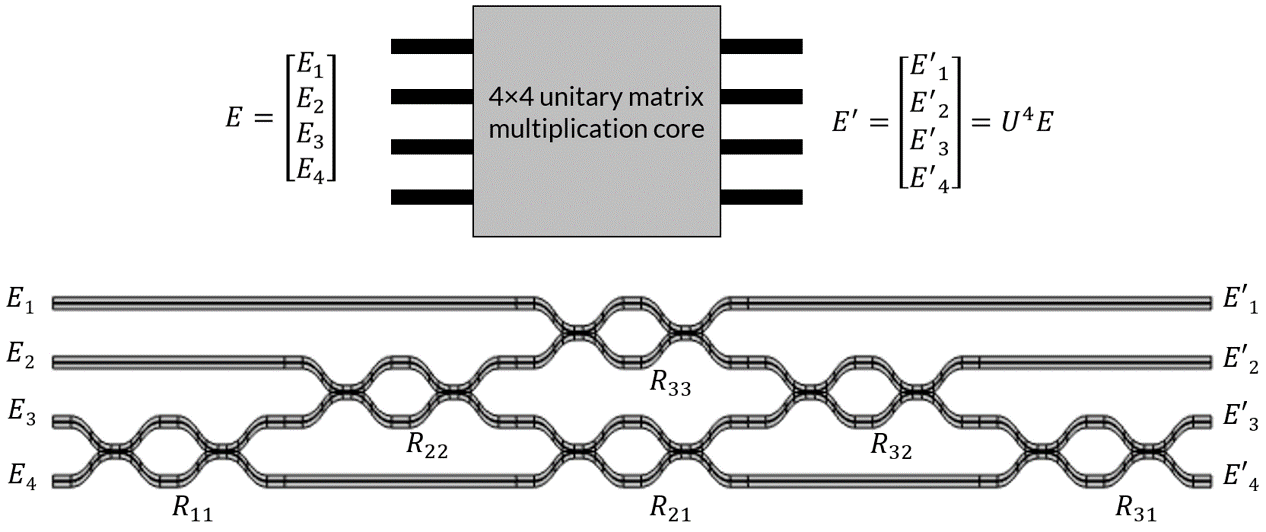
6つの MZI のネットワーク上の4行4列のユニタリ行列乗算コアの回路図.
光 4×4 ユニタリ行列乗算コア. このデバイスは6つの MZI のネットワークで構成されます. 入力ベクトルに対して4行4列のユニタリ行列の乗算を実行します. マトリックスは, 電気光学効果または熱光学効果のいずれかを使用して各 MZI に位相シフトを引き起こすことでプログラムできます.

 

最初の MZI の最初の位相シフターは連続調整されます. これにより, 最初と 2 番目の出力でベクトルの回転が引き起こされます.

nxm 一般行列乗算

これまでのところ, \frac{n(n-1)}{2} のMZI の光ネットワークを使用して, 任意の n 行 n 列のユニタリ行列乗算を実行するまで構築してきました. 明らかに, n 行 n 列のユニタリ行列は非常に特殊なクラスの行列です. 系を一般的に有用なものにするためには, ユニタリ行列と正方行列の場合だけに限定されない, 一般的な n 行 m 列の行列の乗算に取り組む必要があります. これは特異値分解 (SVD) によって可能になります. SVD では, n 行 m 列の行列 M は U\Sigma V^* として因数分解できます. ここで, U は n 行 n 列のユニタリ行列, \Sigma は n 行 m 列の対角行列, V^* は m 行 m 列のユニタリ行列です. ^{*} は複素共役を表します.したがって, M を計算するときは, U に対して 1 つの光ネットワーク, V^* に対して 1 つの光ネットワークがあれば十分です. を作成し, それらを対角行列 \Sigma を表すアテニュエーターの配列に接続します. これは, 対角行列は定数による各要素のスケーリングのみを表すためです. アテニュエーターは, 単一入力と単一出力を備えた MZI で作成することもできます.

光 n 行 m 列の行列乗算デバイスの概略図. m 行 m 列のユニタリ行列乗算コア, n アテニュエーターアレイ, および n 行 n 列のユニタリ行列乗算コアで構成されます. .
光 n × m 行列乗算デバイスは, 2 つのユニタリ行列乗算コアとアテニュエーターアレイで構成されます.

要約すると, 一般的な n 行 m 列の行列乗算用の光学系を構築するために必要な要素がすべて揃っています. n 行 n 列の行列乗算系のモデリング例を以下にリンクします. このモデルは, より複雑な n 行 m 列の行列を構築するためのインスピレーションとして使用できます.

終わりに

このブログでは, 任意の n 行 m 列の行列が, 複数の 2 行 2 列のユニタリ部分行列と対角行列の積として因数分解できることを実証しました. これにより, 一連の MZI を使用して一般的な行列乗算用の光ネットワークを構築できるようになります. また, 集積低損失シリコンフォトニクスを使用して光計算を実行する利点についても学びました.

私たちの将来の携帯電話やコンピューターは, 光プロセッサーまたは光プロセッサーを搭載するのでしょうか? それが分かるまで待つことになりますが, その間, 克服する必要のある技術的な困難はまだたくさんあります. 私たちが確かに知っているのは, マルチフィジックスシミュレーションが高度な光計算系の設計と最適化に不可欠な部分であるということです. このブログで見られるように, COMSOL Multiphysics® のビームエンベロープ法は, 高速な計算時間と優れたメモリ効率で光学的に大規模なモデルをシミュレーションするのに特に適しています. また, 光学系全体をシミュレートすることもできます. これは, 不均一な温度勾配や機械的変形などの他の物理的影響を考慮する場合に重要です.

次のステップ

下のボタンをクリックして, アプリケーションギャラリに移動して, 自由空間マッハツェンダー干渉計と光学ユニタリ行列乗算デバイスのチュートリアルモデルを自分で試してみてください:

チュートリアルモデルを取得

他の参考文献

参考文献

  1. J. Cheng, H. Zhou, and J. Dong, “Photonic Matrix Computing: From Fundamentals to Applications”, Nanomaterials, 11(7), 1683, 2021.

コメント (0)

コメントを残す
ログイン | 登録
Loading...
COMSOL ブログを探索
カテゴリー
タグ