このブログは, 金属基板上に様々な直径のガラスナノピラーを配列した2D反射メタレンズを設計するための, 簡単で教育的なシミュレーションアプリを構築するためのガイドです. このアプリを構築するには, COMSOL Multiphysics®ソフトウェアのアプリケーションビルダーを使用します. このアプリはまず, 与えられた波長に最適なメタサーフェスパラメーターを見つけ, 次にナノピラーの直径と相対位相シフトの関係を計算します. これに基づいて, アプリはメタレンズのジオメトリを自動的に構築し, 最後に, 最終的なジオメトリに対して周波数領域スタディを実行し, 焦点周辺の電場を計算します.
メタレンズとは?
近年, メタマテリアルは, フォトニクスや音響学など, 波動方程式の解法に関わる分野で人気のある研究テーマとなっています. メタマテリアルとは, 通常は波長よりも小さい人工的な構造 (構造単位は“メタ原子”と呼ばれることもある) を持つ複合材料です. このため, メタマテリアルは, 構成材料とは異なる材料特性を持つ均質な材料のように電磁場と相互作用します. 一般的な例として, 電子レンジのドアの格子があります. —空気で満たされた穴のある金属板は, 固体の金属板にも空気にも見られない特性を持つメタマテリアルです. それは, 波長の短い可視光に対してはほとんど透明ですが, 波長の長いマイクロ波は完全に遮断します.
メタマテリアルの主な利点は, 既知の “本物の “材料にはない定性的な特性を提供することに加え, 構造の幾何学的パラメーターを変えることによって, その特性を定量的に, —通常は広い範囲で—調整できることです. フォトリソグラフィーのような半導体製造のために開発された技術の多くは, メタマテリアルの製造にも応用できます. このようなメタマテリアルで作られた光学部品は, 顕微鏡装置やバーチャルリアリティ技術などの用途で非常に求められています.

電子レンジのドアの格子の拡大図.
このブログでは, 反射型メタレンズに焦点を当てます. これは, 凹面鏡のように機能するように設計された金属基板上のガラスナノピラーからなる平面アレイのことです. “メタミラー”の方が適切な名称のように思われるかもしれませんが, このデバイスの動作原理は従来の反射だけでなく, 反射波が座標に依存した位相シフトも受ける異常反射をも含むのです. メタレンズには, レンズやミラーといった従来の光学デバイスと比較して, 以下のような利点があります:
- メタレンズの厚さは1ミクロンの数分の1にすることができ, 光学デバイスの小型化が可能です
- ひとつのメタサーフェスは, 単に光を集めるだけでなく, それ以上のことができるように設計することができます. つまり, 複数の従来の光学デバイスを 1 つの超薄型メタデバイスに統合することが可能になります
- メタマテリアルは, 紫外線 (UV) のような特定の波長範囲で優れた性能を発揮します
より具体的には, 下図に示すように, 高さH, 周期Pは均一で, 直径 D(x)が異なる二酸化ケイ素ナノピラーで構成され, 平らな金属基板の上に配置された2Dメタレンズを考えます. 簡略化のため, 面外方向に偏光した垂直入射の平面波 (負のy方向に動く) のみを見ていきます.
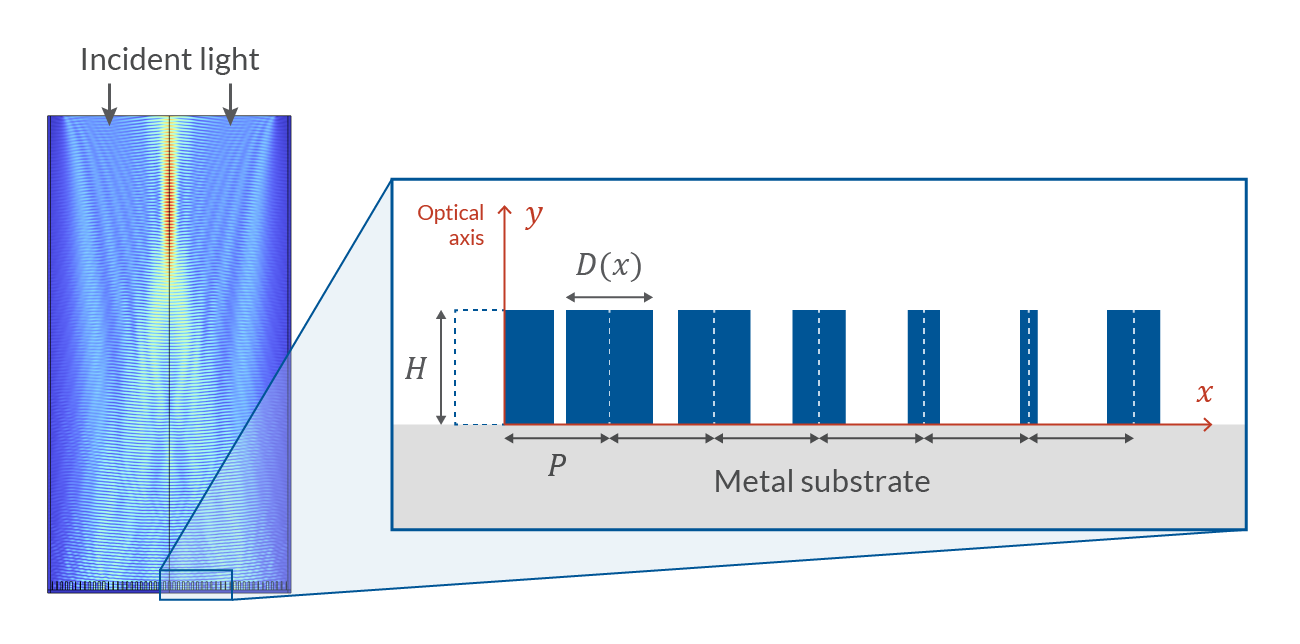
数学的に言えば, 凹面鏡とは, 入射平面波が波の位相を局所的にシフトさせ, 一点に収束する球面波になるようにするデバイスです. 直観的には, ピラーの厚みが増すにつれて, 周囲の空気と比較してピラーの屈折率が高くなるため, 反射波がより大きな位相シフトを拾うことが想像できますが, 機能するメタレンズを作ろうとすれば, 次節で述べるように, 直径と相対位相シフト\Delta \Phi (D)との間の正確な定量的関係を求める必要があります. ここで使った手法は, 参考文献1に基づいています.
ユニットセルシミュレーション
\Delta \Phi (D)を求める効率的な方法は, すべてのナノピラーが直径Dを持つ均一な周期格子による位相シフトを計算し, 直径値の範囲にわたってスイープすることです. (周期構造のモデリングについて詳しくは, こちらをご覧ください.) これにより, 周期的な境界条件を使用することができるようになり, 格子の単一のユニットセルのシミュレーションだけで済みます. 入射波を励起するために周期的なポート境界条件を使用することによって, 複素Sパラメーター S_{11}の引数を通して波の位相シフトに簡単にアクセスすることができます.
機能するメタレンズを構築するには, 波の局所位相を0から2\piラジアンの間で任意の量だけシフトできる必要があります. したがって, まず, できるだけ高い反射率を保ちながら, \Delta \Phi ( D_\mathrm{max} ) – \Delta \Phi ( D_\mathrm{min} )=2 \piとなるようなH, P, 最小直径と最大直径D_\mathrm{min}とD_\mathrm{max}の値を見つける必要があります. これは周波数領域の最適化問題です. 最適化ステップでは, スイープの終点での結果だけが必要なため, 中間ステップを省くことができ, 計算が速くなります. ピラーの幅が狭いほど位相シフトの範囲が広くなること, また, 可能な限り小さなD_\mathrm{min}は製造上の制限に支配されることがわかっているため, D_\mathrm{min}を制御パラメーターとして扱いません. その代わり, D_\mathrm{min}はほとんどの波長で値20~\mathrm{nm}の固定パラメーターとなります (波長300~\mathrm{nm}前後とそれ以下では, 望ましい結果を得るには10~\mathrm{nm}を使用すべきです). 必要なのは相対位相のみなので, 目的関数は次のようになるはずです:
{S_{11}( D_\mathrm{min} )} \right]-2\pi\right|.
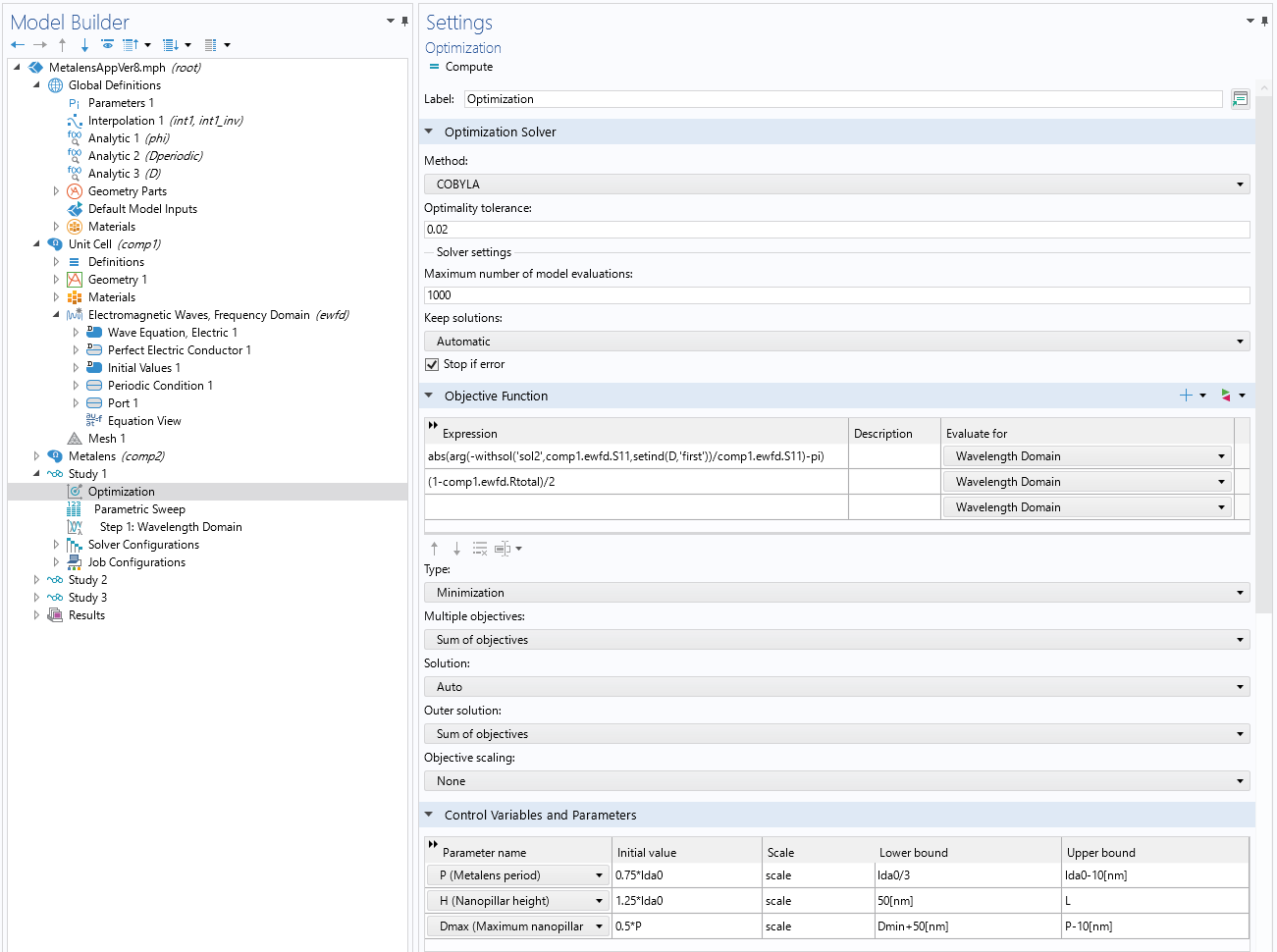
しかし, この式はユーザーインターフェースで使用する準備ができていません. なぜなら, ソフトウェアは正のy方向に伝播する平面波に対して e^{-iky}という符号の規約を使用し, -\piから \piまでの複素数の位相を定義しているからです. COMSOL®の符号の規約を使用し, D=D_\mathrm{min}とD=D_\mathrm{max}の解を参照するために必要な演算子を追加すると, 下図のような式になります. また, これら2つの解から得られる反射率を含む項を目的関数に追加しました. これは, 共振モードを回避し, 効率性を高めるのに役立ちます. 最適化についてさらに詳しく学びたい方は, 電磁気学における形状最適化に関するブログまたはCOMSOL Multiphysics®における最適化の実行に関するオンデマンドコースをぜひご覧ください.
最適化スタディ(スタディ1 )で使用される設定. 最適化ステップでは終点でのスイープ結果を使用するため, モデルビルダーのツリーに示されているように, パラメトリックスイープステップを最適化ステップの後に配置し, withsol()および sentind()演算子を使用して目的の目的関数を実装する必要があります. また, 反射率に関する2つ目の式を目的関数に追加しました.
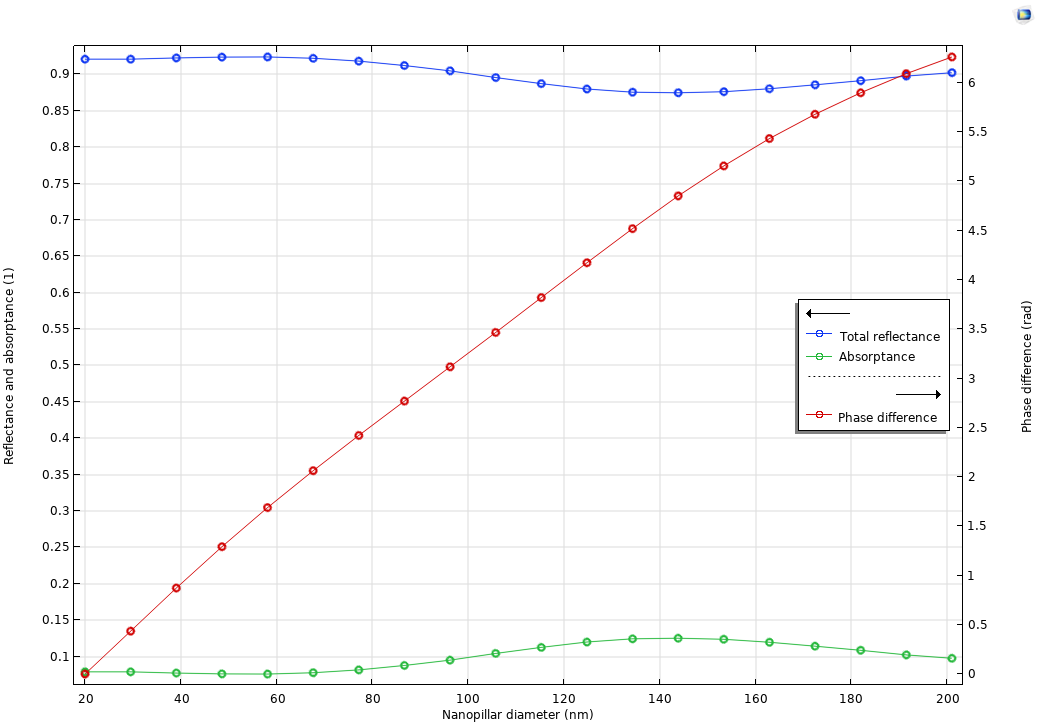
あとは, 最適化されたパラメーター値でフルスイープを実行し, D_\mathrm{min}とD_\mathrm{max}の中間値の位相シフトを求めるだけです. 結果は下図のようになるはずです. 直径の範囲全体を通して, 高反射率を保ち, 単調に増加するきれいな位相シフトが得られます. 次に, これらの結果に基づいてメタレンズを構築します.
400~\mathrm{nm}のユニットセルスイープ結果のプロット. ナノピラーの直径範囲全体を通して高い反射率を保ちながら, 0から2\piまで単調に増加する位相シフトを示しています.
メタレンズシミュレーション
メタレンズのジオメトリを構築する前に, 位相シフト関数\Delta \Phi (D)をナノピラーの直径分布関数D(x)に変換する必要があります. ここで, xは光軸からの距離です. 理想的な集光ミラーは, 垂直入射の平面波に対して次のような位相シフトを適用することがわかっています:
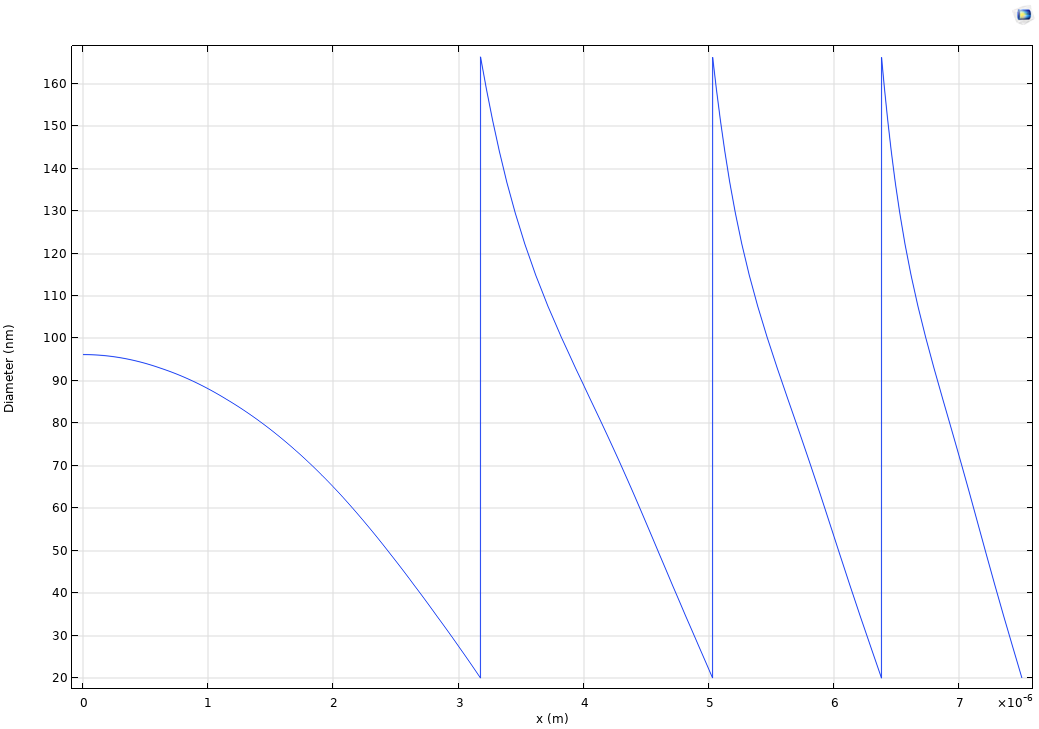
ここで, fとRはそれぞれメタレンズの焦点距離と半径です. 便宜上, \Delta \phi (R) =0となるように\Delta \phi (x)を定義しています. あとはいくつかの数値操作の問題です. 位相シフトが単調であると仮定すると, \Delta \Phi (D)を反転して \Delta \Phi ^{-1} (\phi) \equiv D( \phi )を求め, D( \phi \pm 2n\pi ) =D( \phi )となるように周期性を追加し, \Delta \phi (x)と合成関数を形成してD(\phi(x)) \equiv D(x) を得ることができます. 例として, 下図のようになるはずです.
焦点距離25~\mu\mathrm{m}, 半径7.5~\mu\mathrm{m}, 動作波長 400~\mathrm{nm}のメタレンズの光軸からの距離の関数としてのナノピラー直径分布D(x).
次の課題は, この関数を実際のジオメトリに変換することです. 上記の関数をグローバル定義ノードで定義すると, ピラー位置xを入力とし, 幅をD(x)に設定したジオメトリパーツとしてナノピラーを定義することができます. あとは, このパーツの\lfloor R/P \rfloor (ここでは, Rはメタレンズの半径, Pはメタサーフェスの周期) インスタンスをジオメトリシーケンスに追加するだけです. さらに良い方法は, 次のセクションで説明するように, アプリケーションビルダーを使って, これを行うメソッドを作成することです.
アプリの実装について
まず, メタレンズのジオメトリを自動生成する方法を見てみましょう. 要するに, アプリケーションビルダーでは, メソッドmodel.component(<comp>).geom(<geom>).create(<name>, "PartInstance")を使ってジオメトリパーツのインスタンスを作成し, model.component(<comp>).geom(<geom>).feature(<name>).setEntry. を使って入力パラメーターを設定することができます. これらのコマンドを for ループ内に配置することで, メタサーフェス全体を得ることができます. この方法は, 小さなメタレンズ (R/P\lesssim100)や教育目的には効果的です. 大きなメタレンズの場合は, 段階的サブモデリング手法を使用する必要があります. この手法では, COMSOL®モデルを使用して異なるジオメトリパラメーターに対するユニットセル応答を計算し, その結果をJavaメソッドまたはLiveLink™ for MATLAB®を使用した大きなプログラムの一部として使用します. メソッドの書き方を学んだので,
("inputexpr", <expr-name>, <val>)model.result().numerical("gev1").getReal()を使って初期最適化の出力を受け取り, model.param().set()を使ってモデルのパラメーターをこれらの値に設定するボタンを作ることができます. さらに, setRibbonItemEnabled()を使って, 前のステップが完了してから次のステップのボタンを有効にするようにしました.
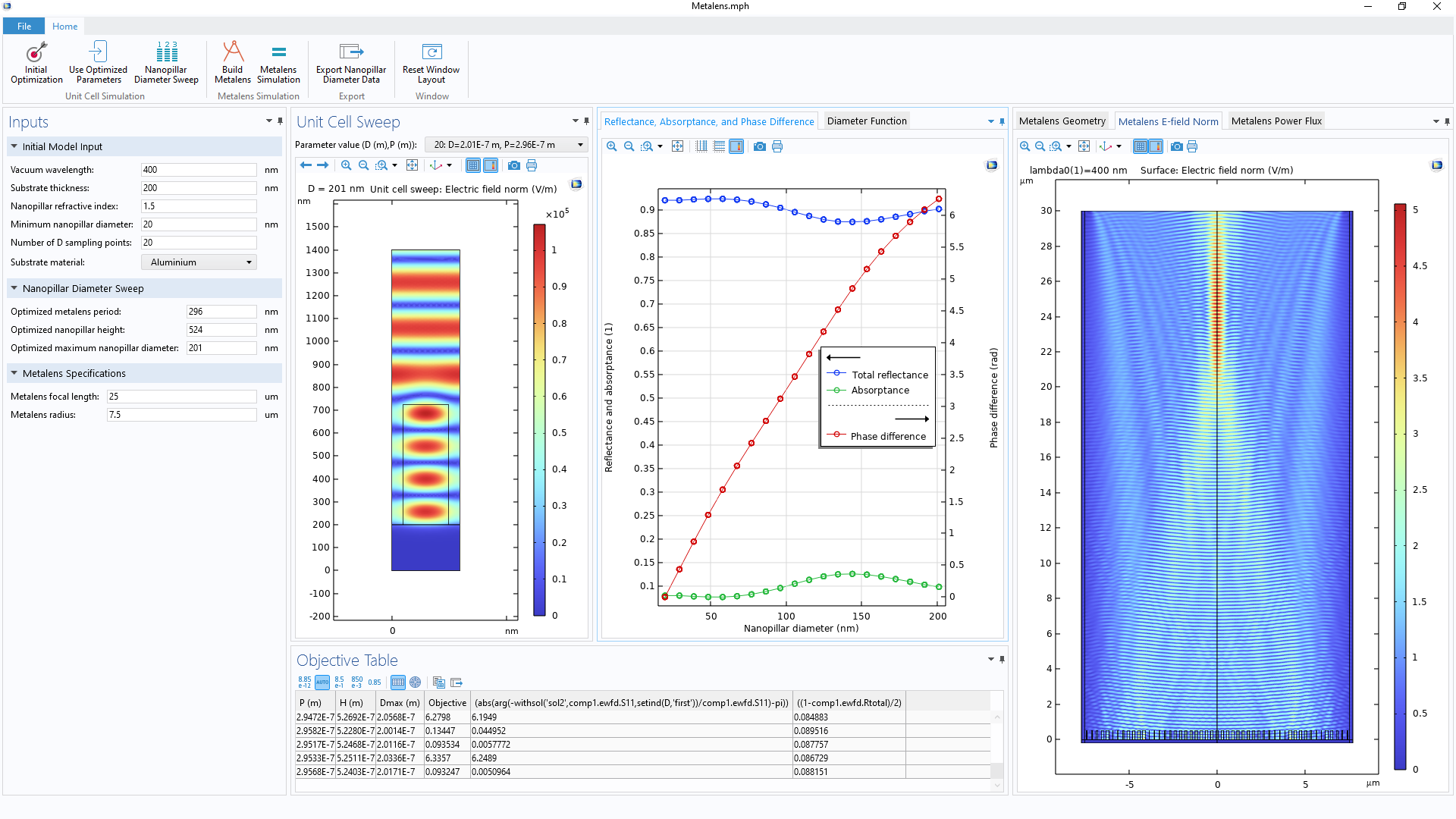
アプリケーションビルダーは, 設計プロセスにおける面倒なステップを自動化するだけでなく, それ以上のことを実現することができます. 例えば, モデルをアプリにパッケージ化することによって, カスタムユーザーインターフェースを作成できることが可能になります. これは, ユーザーが一目で設計プロセス全体を監視できるようになるため, 非常に有益です. 下図はアプリのユーザーインターフェースです. 次のステップとして, COMSOL Compiler™を使ってスタンドアロンのアプリを作成することもできます.
メタレンズアプリのユーザーインターフェース. デザインプロセスのすべての側面を一目で監視できるように設計されています.
動作中のメタレンズアプリの画面録画.
おわりに
このブログでは, 指定されたサイズ, 焦点距離, 動作波長を持つ2D反射メタレンズの設計に使用できるアプリの構築方法をまとめました. COMSOL Multiphysics®のアプリケーションビルダーを使用することで, ユーザーが設計プロセスの最初から最後まで便利に監視できるユーザーインターフェースを使用して, 比較的複雑な設計プロセスを合理化できることがわかりました.
しかしながら, まだメタレンズ設計の表面を擦ったに過ぎません. さらなる拡張として, レンズ性能解析 (例えば, 文献1で解析されたような焦点の大きさや分散特性) を含む3Dレンズの検討や, 文献2のような熱的に構築可能なメタレンズをモデル化するためのマルチフィジックスなどがあります. 今後のブログで, これらのより高度なトピックのいくつかを取り上げていきたいと思います.
次のステップ
下のボタンをクリックするとアプリケーションギャラリに移動できるので, メタレンズアプリをご自分でお試しください.
参考文献
- H. Guo et al., “Design of Polarization-Independent Reflective Metalens in the Ultraviolet–Visible Wavelength Region,” Nanomaterials, vol. 11, no. 5, 2021; https://doi.org/10.3390/nano11051243.
- A. Archetti et al., “Thermally reconfigurable metalens,” Nanophotonics, vol. 11, no. 17, pp. 3969–3980, 2022; https://doi.org/10.1515/nanoph-2022-0147.
Oracle および Java は, Oracle および/またはその関連会社の登録商標です. MATLAB はThe MathWorks, Inc. の登録商標です.



コメント (0)