電熱解析におけるよくある落とし穴

電力伝送や民生用電子機器などの用途では, 温度非線形性を持つ材料 (つまり, 材料の電気伝導率と熱伝導率が温度によって変化する材料) の電磁加熱をモデル化することが非常に重要になる場合があります. これらの非線形性をモデル化する場合, 経験豊富な解析者であっても, 非線形材料特性, 境界条件, 形状の組み合わせにより, 全く予期しない結果になることがあります. 非常に簡単な例で, その理由を見てみましょう.

オームの法則と抵抗加熱の理解

エンジニアとして最初に学ぶ物理法則の一つがオームの法則です. デバイスを流れる電流は, 印加電圧差をデバイスの電気抵抗で割った値, つまり I = V/R_e に等しくなります. ここで, 電気抵抗 R_e は, デバイスの形状と材料の電気伝導率の関数です.

この法則を学んだ直後に, デバイス内で消費される電力についても学んだことでしょう. これは電流と電圧差の積, つまり Q = IV に等しく, Q = I²R_e または Q = V²/R_e と表記することもできます. おそらく学習の少し後で, 熱伝導率と等価デバイス熱抵抗 R_t についても学びました. これにより, 周囲条件に対するデバイスの温度上昇を ΔT = QR_t として集中的に計算できます. その後, T = T_{ambient} + QR_t を使用してデバイスの絶対温度を決定できます.

この点から議論を開始し, デバイスの完全な集中モデルを検討します. (はい, 非常に単純なところから始めますので, この部分では COMSOL Multiphysics® ソフトウェアを使用する必要さえありません!) 電気抵抗 R_e = 1 Ω, 熱抵抗 R_t = 1 K/W の集中デバイスを考えてみましょう. このデバイスを定電圧で駆動して温度を T = T_{ambient} + (V^2 / R_e) R_t として計算するか, ピーク温度が T = T_{ambient} + I^2 R_e R_t である定電流で駆動することができます.

周囲温度は室温とほぼ同じ 300 K (27°C) とします. では, 下の図に示すように, 電圧 (0 V から 10 V) と電流 (0 A から 10 A) の増加に対するデバイス全体の温度をプロットしてみましょう. 当然のことながら, 温度は2乗関数的に上昇します.

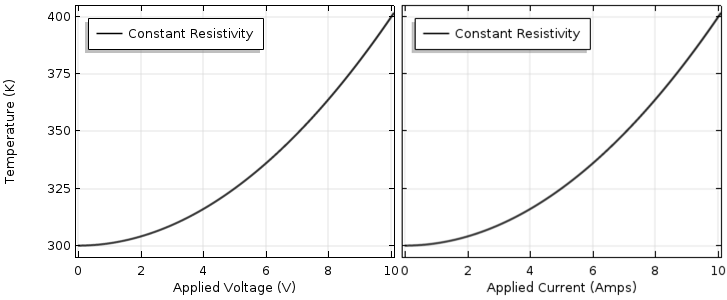
デバイスの温度は, 印加電圧 (左) と印加電流 (右) の関数として表されています. 特性は一定と仮定しています.

この曲線を使えば, より広範囲の動作条件を予測できると考えるかもしれません. デバイスを故障温度 (材料が溶融または蒸発する温度) まで駆動するとします. この材料は, 温度が 700 K (427°C) に達すると蒸発すると仮定します. この曲線に基づくと, 簡単な計算で最大電圧は 20 V, 最大電流は 20 A と推測できますが, これは全くの誤りです!

単純な集中モデルへの材料非線形性の導入

ここまで読んで, おそらく皆さんは私たちが犯した単純な間違いを指摘する準備が整ったことでしょう. 電気抵抗は温度に対して一定ではありません. ほとんどの金属では, 電気伝導率は温度上昇とともに低下しますが, 抵抗率は伝導率の逆数であるため, デバイスの抵抗率は上昇します. そこで, 抵抗率に温度依存性を導入してみましょう:

これは 線形化抵抗率モデル と呼ばれ, ρ₀ は基準温度における基準抵抗率, T^e_0 は電気抵抗率の温度係数です.

ρ₀ = 1 Ω, T^e_0 = 300 K, α_e = 1/200 K とします. すると, デバイス温度が 300 K のときに抵抗は 1 Ω になり, 設定温度より 200 K 上昇すると抵抗は 2 Ω になります. 電圧と電流の関数としての温度集中方程式は, 以下のようになります:

および

これらの方程式は少し複雑ですが (最初の方程式は T に関する二次方程式です), 手計算で解くことは可能です. 電圧と電流の増加に対する温度のグラフを以下に示します.

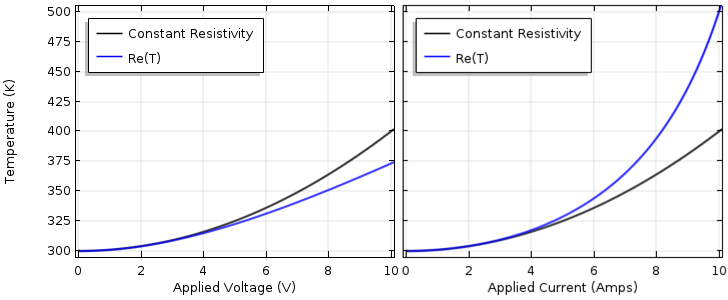
印加電圧 (左) と印加電流 (右) の関数としてのデバイス温度と, 温度の関数としての電気抵抗率.

電圧駆動の問題では, 温度が上昇すると抵抗が増加します. 抵抗は温度式の分母に現れるため, 抵抗が増加すると温度が低下し, 一定の抵抗率の場合よりも温度が 低く なります. デバイスを定電流で駆動すると, 温度に依存する抵抗が分子に現れます. 電流が増加すると, 抵抗による発熱は線形材料の場合よりも 大きく なります.

この時点で, このデバイスが耐えられる最大電圧または最大電流を計算したくなるかもしれませんが, おそらく2つ目の間違いに気づいているでしょう. 熱抵抗の温度依存性も考慮する必要があります. 金属の場合, 電気伝導率と熱伝導率は同じ傾向を示すと想定するのが妥当です. そこで, 以前使用したのと同様の非線形式を使用しましょう:

これで, 電圧駆動と電流駆動の温度方程式は次のようになります:

および

以前とわずかに異なるだけですが, これらの非線形方程式を解くのはかなり難しくなりました. シミュレーションソフトウェアがますます魅力的になってきました! これらの方程式を解くと (r₀ = 1 K/W, α_t = 1/400 K, T^t_0 = 300 K と設定します), 下図のようにデバイス温度をプロットできます.

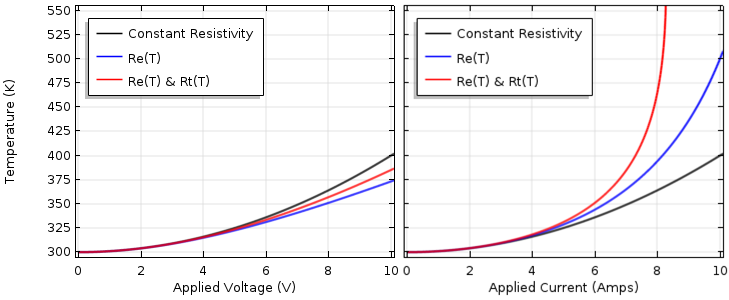
印加電圧 (左) と印加電流 (右) の関数としてのデバイス温度と, 温度の関数としての電気抵抗率および熱抵抗率.

電流駆動の場合, 温度が漸近的に上昇することに注目してください. 電気抵抗と熱抵抗はどちらも温度上昇に伴って増加するため, 電流が増加するとデバイスの温度は急激に上昇します. 温度が無限大に上昇すると, 問題は求解できなくなります. これは実際には完全に予想されたことであり, 実際, これが基本的な自動車ヒューズの仕組みです. さて, この問題を COMSOL Multiphysics で解く場合, 過渡モデル (デバイス密度と比熱による熱質量を組み込む) として解き, デバイスの温度が故障点まで上昇するのにかかる時間を予測することもできます.

幸いなことに, 電圧駆動の場合は状況が少し単純になります. ここでも予測可能な動作が見られます. つまり, 熱抵抗の上昇により, 温度に依存する電気伝導率のみを考慮したときよりも温度が上昇します. ここで興味深いのは, 温度が依然として一定の抵抗率の場合よりも低いことです. これも時々人々を混乱させますが, これらの非線形性の1つが温度を 下げ, もう1つが温度を 上げる ということを覚えておいてください. 一般に, より複雑なモデル (COMSOL Multiphysics で構築するようなモデル) では, どちらの非線形性が優勢になるかはわかりません.

ここで他にどのような間違いを犯した可能性がありますか? 熱抵抗率の温度係数を 正 としました. これはほとんどの金属では確かに当てはまりますが, ガラスなどの一部の絶縁体ではその逆が当てはまります. 通常, デバイス全体の熱抵抗は, 導電性ドメインではなく, 主に絶縁体の関数です. さらに, デバイスの熱抵抗には, 周囲の環境への冷却の影響も組み込む必要があります. したがって, 自由対流 (温度差とともに増加する) と放射 (温度差に4次依存) の影響も, この単一の熱抵抗にまとめることができます. ここでは, 問題を (比較的) 単純なものとして, 熱抵抗温度係数 α_t = -1/400 K の符号を入れ替え, 最大 100 V の電圧と最大 100 A の電流を駆動する場合の電圧駆動と電流駆動のケースを直接比較してみましょう.

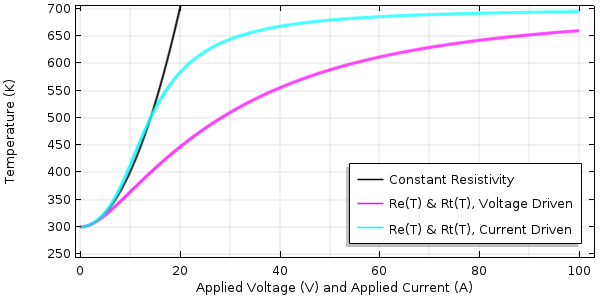
熱抵抗温度係数が負の場合のデバイス温度を, 印加電圧 (ピンク) と印加電流 (青) の関数として示します.

ここで, かなり異なる結果がいくつか見られます. 電圧駆動と電流駆動の両方のケースにおいて, 低負荷では温度がほぼ2乗的に上昇しますが, 高負荷では熱抵抗率の低下により温度上昇が平坦化し始めます. 傾きは常に正ですが, 大きさは減少しています. 電流駆動の場合は漸近的に T = 700 K に近づき始めますが, 電圧駆動の場合は破壊温度より大幅に低い温度に留まります.

これは重要な結果であり, よくあるもう1つの間違いを浮き彫りにしています. ここで電気抵抗率と熱抵抗率に使用した非線形材料モデルは 近似値 であり, 700 K に近づきすぎると無効になり始めます. この領域で動作させることが予想される場合は, 文献に戻ってより洗練された材料モデルを見つける必要があります. 既存の非線形材料モデルは確かに解けましたが, 計算された動作温度でそれらが依然として有効であることを常に確認する必要があります. もちろん, これらの動作条件に近くない場合は, 線形化抵抗率モデル (COMSOL Multiphysics に組み込まれている材料モデルの1つ) を使用できます. そうすれば, モデルは有効になります.

これで, すべてのデータから, 温度と駆動電圧または電流の間に非常に複雑な関係があることがわかります. 非線形材料を考慮すると, 温度は定数特性を使用する場合よりも高くなったり低くなったりする可能性があり, 温度応答の傾きは動作条件に基づいて非常に急峻なものから非常に緩やかなものまで変化します.

これらの結果に, まだ完全に混乱していませんか? 抵抗式の係数の1つを変更したらどうなるでしょうか? 一部の材料は, 電気抵抗と熱抵抗の温度係数が負です. さらに複雑な非線形性を使用したらどうなるでしょうか? この単純な集中定数デバイスのケースでさえ, 予想される温度変化について自信を持って言えるでしょうか? それとも, 厳密な計算で確認した方が良いでしょうか?

電気熱解析における一般的な落とし穴に関する結論

現実世界のデバイスの場合はどうでしょうか? 多種多様な材料, 温度に応じて異なる電気伝導率と熱伝導率, そして複雑な形状が組み合わさったデバイスです. 温度上昇にかかる時間を調べるために, 定常状態のみでモデル化しますか, それとも時間領域でモデル化しますか? おそらく (実際, ほとんどの場合), 放射 や 自由対流 といった非線形境界条件も存在するでしょう. これらの条件は, 単一の集中熱抵抗では近似できません. では, 何が期待できるでしょうか? ほぼあらゆることが考えられます! そして, どのように解析するのでしょうか? もちろん, COMSOL Multiphysics を使います!

次のステップ

COMSOL Multiphysics が, マルチフィジックスモデリングと解析の目標達成にどのように役立つか, ぜひ評価してください. 下のボタンからお問い合わせください.