
COMSOL Multiphysics® ソフトウェアでモデルを解いた後, シミュレーション領域で定義された一連の関数に解データを適合させたい場合があります. 前回のブログでは, 離散経験データを曲線に当てはめる方法を説明しましたが, ここでは代わりに連続解データの当てはめを検討します. 次に, 直交性の概念を導入し, 解データを一連の直交関数に当てはめることが, どのようにして単純で便利な後処理操作に帰着するのかを説明します.
カーブフィッティングの利点
離散実験データのフィッティングに関する以前のブログで, カーブフィッティングがその後のシミュレーション作業にどのように役立つかを説明しました. 例えば, 生の実験データを使用して材料特性を直接定義しようとすると, データの統計的揺らぎによってソルバーが収束しにくくなります. さらに, 離散データを滑らかな関数にフィッティングすることで, その関数の高次導関数にアクセスすることができます. 一方, 生のデータを数値的に微分しようとすると, 非常にノイズが多くなり, エラーが発生しやすくなります.
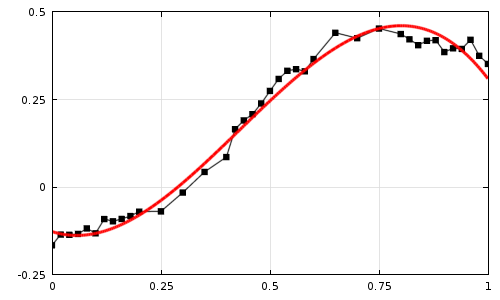
生の実験データ (黒い点) を3次多項式 (赤い曲線) に当てはめたもの.
COMSOL Multiphysics モデルでの以前のスタディからの解データへの曲線フィッティングについてはどうでしょうか? 直接的な利点の1つはデータの圧縮です. 完全な解とよく一致する関数の線形結合を見つけることができれば, いくつかの関数係数の値を共有するだけで, その完全な解から多くの情報を伝達することができます. (データ圧縮には万能の戦略はないことに注意してください. プローブテーブルや選択の使用など, 他のいくつかのアプローチについては, このモデルに保存される解データの量の削減に関するナレッジベースエントリで説明されています.)
さらに, 連続解データの曲線近似は, 解の高次の空間導関数を推定する便利な方法です. COMSOL® ソフトウェアの多くのフィジックスインターフェースは, 区分的なラグランジュ多項式で構成される有限要素離散化を使用します. デフォルトでは, 多くの場合2次です. この場合, 導関数は必ずしも連続であるとは限らず, 3次以上の導関数は常に0になります.
最小二乗フィッティングの概要
まず, 単純な最小二乗近似の基礎となる数学を見てみましょう. Ω で示すいくつかのシミュレーションドメイン (または境界またはエッジ) で, COMSOL Multiphysics モデルがフィールド変数 u を求解したと仮定します. 私たちの目標は, 事前定義された関数の集合の線形結合として扱うことによって, この領域にわたる u の値を近似することです.
ここで, fi は一連の既知の関数であり, ci は求解する必要がある係数です.
これらの未知の係数を決定する一般的な方法は, u とその近似値の差の L2 ノルムを取得することです.
次に, この L2 ノルムの極小値に対応する ci の値を見つけます.
Ω 内の極小値では, 未知の係数に関する導関数はゼロに等しくなければなりません.
ここで, 添え字 j は, 合計のインデックスとの混同を避けるために使用されます.
整数記号の下にあるものはすべて十分に良好であると仮定すると, 連鎖規則を適用すると, これは次のように単純化されます.
先頭の係数2を削除し, 積分と離散合計の順序を入れ替えると, 次の結果が得られます.
この最後の結果は, N 個の未知の係数に対する N 個の線形方程式系です. たとえば, 3つの多項式がある場合, この結果を行列形式で書き出すことができます.
&\begin{bmatrix}
A_{11} & A_{12} & A_{13}\\
A_{21} & A_{22} & A_{23}\\
A_{31} & A_{32} & A_{33}
\end{bmatrix}
\begin{bmatrix}
c_1\\
c_2\\
c_3
\end{bmatrix}
=
\begin{bmatrix}
B_1\\B_2\\B_3\\
\end{bmatrix}\\
&A_{ij} \equiv \int_\Omega f_i(\mathbf{r})f_j(\mathbf{r})\textrm{d}\Omega
\qquad B_{j} \equiv \int_\Omega u(\mathbf{r})f_j(\mathbf{r})\textrm{d}\Omega
\end{aligned}
したがって, 未知の係数についてこの方程式系を解くには, N(N+3)/2 積分を評価する必要があります. (左側の行列が対称であることに注意してください. fifj の積分は fjfi の積分に等しく, N 個の線形代数方程式系の解.)
次のセクションで説明するように, 対応する関数 fi を定義すると, 係数 ci の計算が大幅に簡単になります. 従って, 解データを当てはめようとしている領域で直交します.
直交関数の概要
直交性の概念について議論する際には, 過度に狭い定義を与えないように注意する必要があります. 一般に, あるベクトル空間に属する2つの異なるベクトル u と v は, ベクトル空間は内積 \langle u,v\rangle if \langle u,v\rangle = 0 のもとで直交します. 内積の正確な定義は, ベクトル空間に応じて変わる可能性があります.
ここでは, 空間的に変化する解ベクトルをn次元の実座標空間 (\mathbf{r}\in\mathbb{R}^n) の領域 Ω における関数の集合 f1(r), f2(r), … fN(r) に曲線近似することについて話しているので, 次のこと, より具体的には, これらの関数の内積, を次のように定義できます.
ここで, w(r) は未定義の重み関数であり, Ω のすべての r で w(r) > 0 です.
たとえば, 関数 f_1(x) = 1, f_2(x) = \sin x, および f_3(x) = \cos x は内積の下で直交します.
つまり, 領域 Ω は1次元区間 x\in[-\pi,\pi] であり, 重み関数は単純に w(x)=1 です. 積分を評価することで, これらの関数の直交性を証明できます.
\int_{-\pi}^\pi (1)^2 \textrm{d}x &= 2\pi \qquad \int_{-\pi}^\pi (\sin x)^2 \textrm{d}x = \pi \qquad \int_{-\pi}^\pi (\cos x)^2 \textrm{d}x = \pi \\
\int_{-\pi}^\pi (1)(\sin x) \textrm{d}x &= 0 \qquad \int_{-\pi}^\pi (1)(\cos x) \textrm{d}x = 0 \qquad\int_{-\pi}^\pi (\sin x)(\cos x) \textrm{d}x = 0\\
\end{aligned}
実際, この概念をさらに拡張して, 関数 \sin(2x), \cos(2x), \sin(3x), \cos(3x), なども同じ内積で直交します. これらの三角関数の直交性は, フーリエ級数展開の基礎です.
直交関数を使用した最小二乗フィッティング
ここで, 直交関数について知っていることを利用して, 線形最小二乗フィッティング問題を再検討してみましょう. これは, 前に見たように, 以下を満たす係数の集合 ci を解くことに帰着します.
ここで, 関数 fi が内積の下ですべて直交すると仮定します.
お気づきかもしれませんが, n 次元ベクトル空間の内積について話すとき, 内積の定義に微分要素dΩを使用しましたが, dΩ は次のようになります. 選択した座標系 (デカルト座標系, 円筒極座標系, 球面極座標系など) に応じて表現方法が異なります. 後に例で説明するように, 最大限の便宜を図るために, 重み関数が使用されている座標系のヤコビ行列式に等しい内積の下で直交する関数の集合を選択できます.
関数の直交性により, 左側の N \times N 行列の非対角項はすべて消え, N 個の方程式は, ci の値を直接与える N 個の式の集合になります:
上記の式の分母が1になるように関数を正規化することを選択すると, さらに単純な式が得られます.
したがって, 解データを一連の N 個の関数に当てはめるタスクは, N 個の異なる積分を評価するタスクに縮小されました. COMSOL® ソフトウェアでは, 積分カップリングを簡単に定義して, ジオメトリ内のドメイン, 境界, エッジ, または点の集合にわたる積分を評価できます. (積分カップリングを定義した後にスタディを再実行する必要はありません. 解の更新をクリックするだけで十分です.)
残りのセクションでは, より実用的な例, つまりミラーの変形を一連のゼルニケ多項式に当てはめる例を見ていきます.
ゼルニケ多項式
光学分野で最も一般的に使用される直交関数の1つは, 円の動径座標と方位角の関数であるゼルニケ多項式です.
ここで
- ρ は動径座標 (0\leq\rho\leq 1)
- θ は方位角 (0\leq \theta < 2\pi)
- N_n^m は規格化項
- R_n^{|m|}(\rho) は動径項
- M(m\theta) は仰角項または方位角項
- n は動径指数 (n \in \left\{0,1,2,\dots\right\})
- m は仰角または方位角指数 (ある n に対して, m \in \left\{-n, -n+2, -n+4, \dots , n-2, n\right\})
ゼルニケ多項式の定義方法とその指数の解釈方法には, いくつかの異なる標準形式があることに注意してください. COMSOL Multiphysics® で使用される関数定義は, 2つの別個の指数を使用して関数の動径依存性と方位角依存性を記述しており, ANSI および ISO 規格と一致しています (参考文献1, 2). ゼルニケ多項式は単位円に関して定義されることがよくありますが, ρ を ρR に置き換えることにより, 半径 R の他の円上でも定義できます (ただし, これは 正規化に影響します.).
最初のいくつかのゼルニケ多項式を以下に示します.
| 項 | 式 | 一般名称 |
|---|---|---|
| Z_0^0 | 1 | ピストン |
| Z_1^{-1} | 2\rho \sin(\theta) | 垂直チルト |
| Z_1^1 | 2\rho \cos(\theta) | 水平チルト |
| Z_2^{-2} | \sqrt{6}\rho^2 \sin(2\theta) | 斜めアスティグマ |
| Z_2^0 | \sqrt{3}\left(2\rho^2-1\right) | デフォーカス |
| Z_2^2 | \sqrt{6}\rho^2 \cos(2\theta) | アスティグマ |
| Z_3^{-3} | \sqrt{8}\rho^3 \sin(3\theta) | 斜めトレフォイル |
| Z_3^{-1} | \sqrt{8}\left(3\rho^3-2\rho\right)\sin(\theta) | 垂直コマ |
| Z_3^1 | \sqrt{8}\left(3\rho^3-2\rho\right)\cos(\theta) | 水平コマ |
| Z_3^3 | \sqrt{8}\rho^3 \cos(3\theta) | 水平トレフォイル |
| Z_4^{-4} | \sqrt{10}\rho^4\sin(4\theta) | 斜めクアドラフォイル |
| Z_4^{-2} | \sqrt{10}\left(4\rho^4-3\rho^2\right)\sin(2\theta) | 斜め2次アスティグマ |
| Z_4^0 | \sqrt{5}\left(6\rho^4-6\rho^2+1\right) | 球面収差 |
| Z_4^2 | \sqrt{10}\left(4\rho^4-3\rho^2\right)\cos(2\theta) | 2次アスティグマ |
| Z_4^4 | \sqrt{10}\rho^4\cos(4\theta) | 水平クワッドフォイル |
正規化項は次のように選択されています.
ここで, クロネッカーデルタ δ は, 2つの添え字が等しい場合は1に等しく, そうでない場合は0に等しくなります.
前述の用語に従って, ゼルニケ多項式は重み関数 w(\rho,\theta)=\rho の下で単位円上で直交します. デカルト極座標と円筒極座標の間で変換するときに, 重み関数 ρ がたまたまヤコビアン行列式と正確に一致すると便利です. \textrm{d}\Omega = \rho\textrm{d}\rho\textrm{d}\theta.
ゼルニケ多項式は光学コミュニティで広く使われています. もし眼科に行かれたことがあれば, “アスティグマ” (Z_2^{\pm 2}) や “コマ” (Z_3^{\pm 1}), という言葉を聞いたことがあるかもしれません. また, “近視” や “遠視” という言葉は単に異なる符号の ”デフォーカス” 項 (Z_2^0) を表すものです.
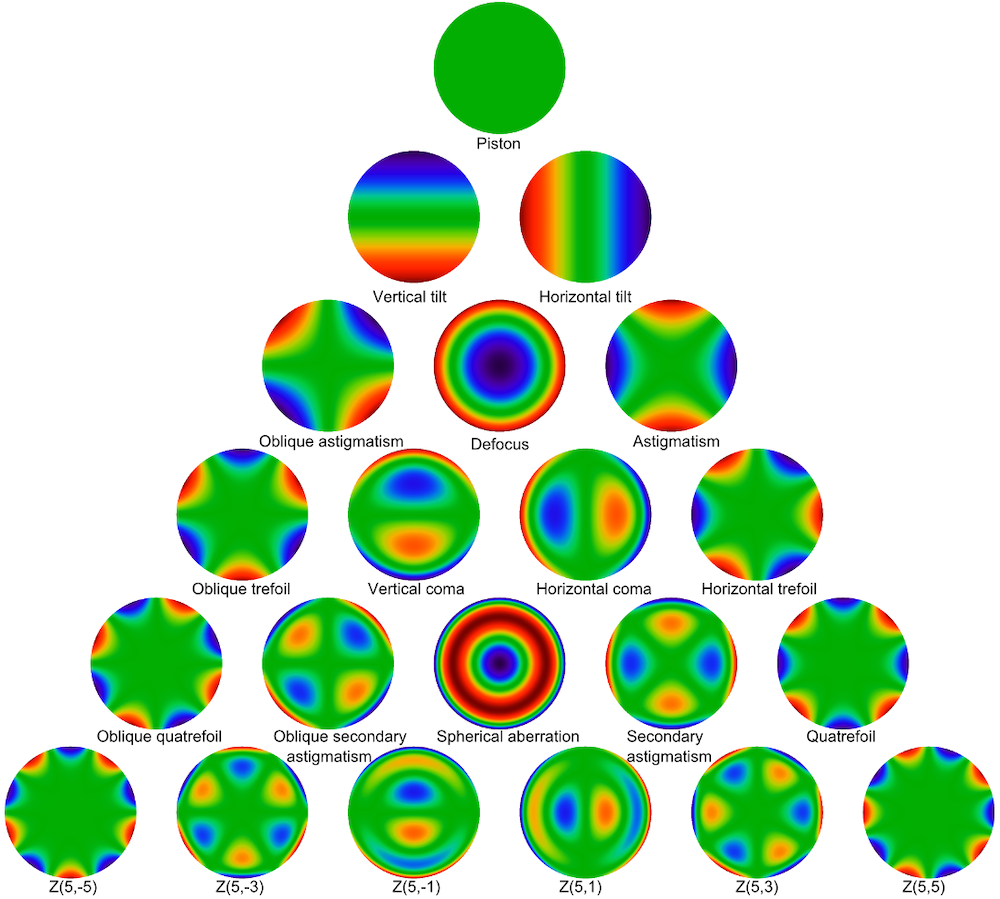
5次までのゼルニケ多項式のプロット
ゼルニケ多項式を使用した変形ミラーの表現
最後に, 知識を問題例で活用してみましょう. 形状は, 側面と底面が固定された平らな円筒形のミラーですが, 上面は自由に変形できます. レンズが均一に加熱されて熱応力が発生し, ミラーの上面が膨張します.
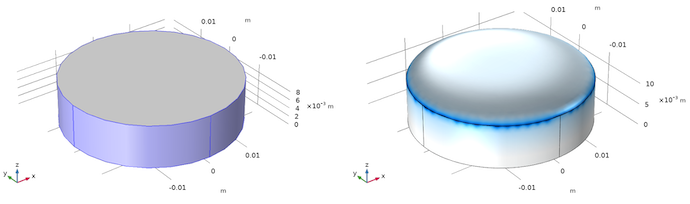
変形していないミラー (左) と変形したミラー (右) のジオメトリ
ミラーの変形した表面の変位場に最もよく適合するゼルニケ多項式係数を計算したいと考えています. 次のスクリーンショットに示すように, 完全を期すために4次までのすべてのゼルニケ多項式を含めますが, 仰角指数が0の項 (ピストン Z_0^0 のみを含めます. デフォーカス Z_2^0, 球面収差 Z_4^0) は, 変位場の対称性により重要な役割を果たします. 変位の積を各ゼルニケ多項式と積分するために, 変形表面上で積分カップリングが定義されます. 次に, いくつかの変数ノードを使用して, 各ゼルニケ多項式と解ベクトルの積の積分を定義し, 対応するゼルニケ係数の値を決定します.
最後に, ミラーの中心から半径方向外側に伸びるカットライン上に変位場 w の面外成分をプロットし, それをゼルニケ多項式の線形結合と比較します. 次のプロットは, ピストン, デフォーカス, 球面収差の項の個々の組み合わせを示し, またそれらの線形結合を変位場と比較します. 解とゼルニケ多項式近似の間の一致は非常に良好であるように見えますが, Z_6^0 などの高次の項を含めることでさらに改善できる可能性があります.
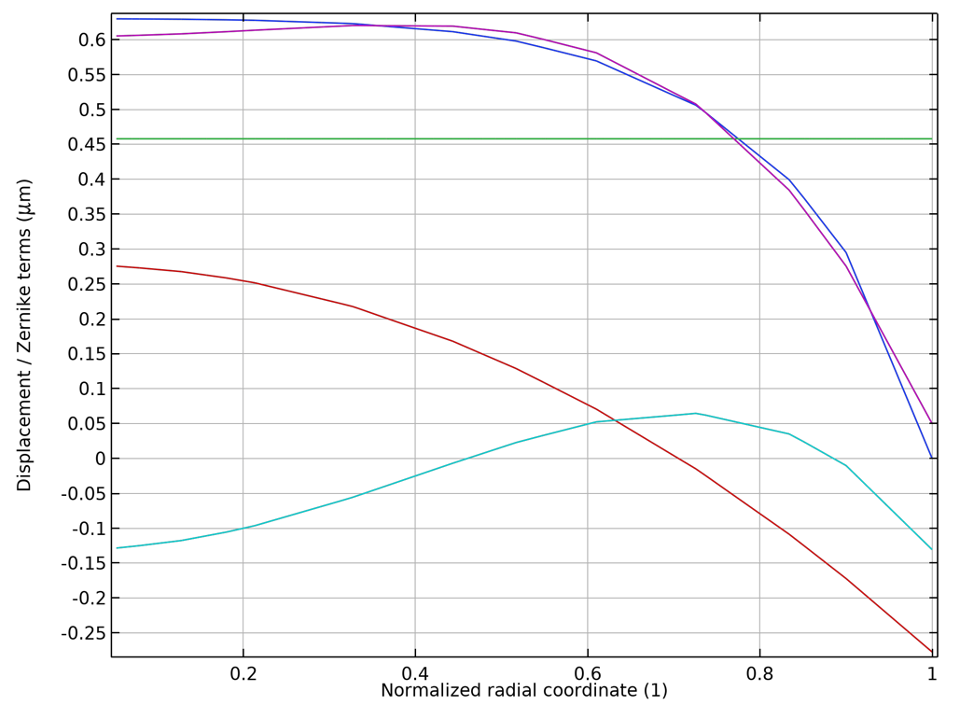
変位場 (青) とゼルニケ多項式フィット (紫) の比較. ピストン (緑), デフォーカス (赤), 球面収差 (シアン) の項も個別に表示されます.
結論
カーブフィッティングは実験データの統計ノイズを平滑化するための優れたツールですが, モデル解自体に適用することもでき, 大きな効果をもたらします. 一連の事前定義された関数, 特に直交関数に解データを適合させると, データ圧縮の迅速かつ便利な手段が提供されます.
次のステップ
下のボタンをクリックして, このブログで説明したモデルを自分で試してみてください. アプリケーションギャラリのエントリとダウンロード可能な MPH ファイルが表示されます.
参考文献
- ISO 24157:2008: Ophthalmic optics and instruments — Reporting aberrations of the human eye, International Organization for Standardization, Geneva, Switzerland. Amendment 1, ibid., 2019.
- ANSI Z80.28-2017: American National Standard for Ophthalmics — Methods of Reporting Optical Aberrations of Eyes. American National Standards Institute, Alexandria, VA.


コメント (0)