
電池の放電中, 回路内の電流は正極から負極へ流れます. オームの法則によれば, これは電流が電場に比例することを意味し, 電流は正電位から負電位へ流れることになります. しかし, 電池内部では何が起きているのでしょうか? 電流は負電位から正電位へ流れるのでしょうか? このブログでは, 放電および再充電中の電池内部の電位プロファイルについて説明します.
電池内の電流
私は, 学校で電気システムを学んだときの物理の授業を覚えています. オームの法則を学びました. これは, 電流は正電位から負電位へ流れ, 電子は反対方向に動くというものです. キルヒホッフの法則は, 電流には連続性が必要であること, つまり電流がシステムから “消える” ことはないことを教えてくれました. ところが, 正極, 負極, 分離電解質を備えた電池の内部構造を見ると, そこではこれらの2つの法則をうまく説明できなくなったのです. 私たち生徒が彼の説明を理解できなかったのかもしれません.
図 1 は, このジレンマを示しています. 放電中, 外部回路では電流 (I) が正極から負極に流れることがわかっています. 電池内では, 電流は負電位から正電位に流れるのでしょうか. それとも, 電池内では電流の連続性が維持されないのでしょうか. 答えは明らかです. オームの法則だけでは, 電池内で何が起こるかを説明できません. 当時の若い学生にとって謎だったことは, いわゆる電気二重層によって説明できました.
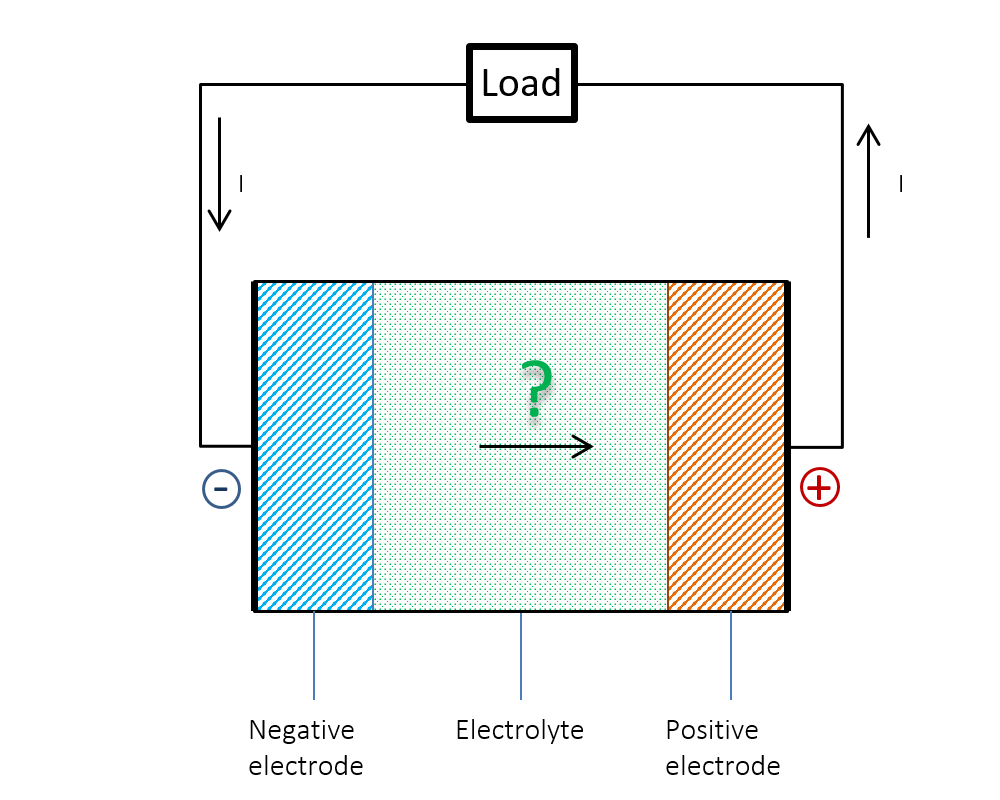
図 1. 電池内では電流はマイナス電位からプラス電位に流れるのでしょうか?
電池の電気二重層構造
金属片を電解質, たとえば溶解した塩を含む溶液に浸すと何が起こるかを見てみましょう. 金属の種類と構造に応じて, イオンは金属と電解質の界面に吸着されます. 金属に隣接する最初の層は通常, 溶媒分子で構成されますが, 溶媒の鞘を持たないイオンも接触吸着されることがあります. この場合, 負イオンは負に帯電した表面に接触吸着されることに注意してください. この溶媒分子と接触吸着イオンの層は, 内部ヘルムホルツ面 (IHP) で示されます. 図 2 を参照してください. 金属表面と反対の電荷を持つ溶媒和イオンは, 外部ヘルムホルツ面 (OHP) で示される追加の外層を形成する場合があります.
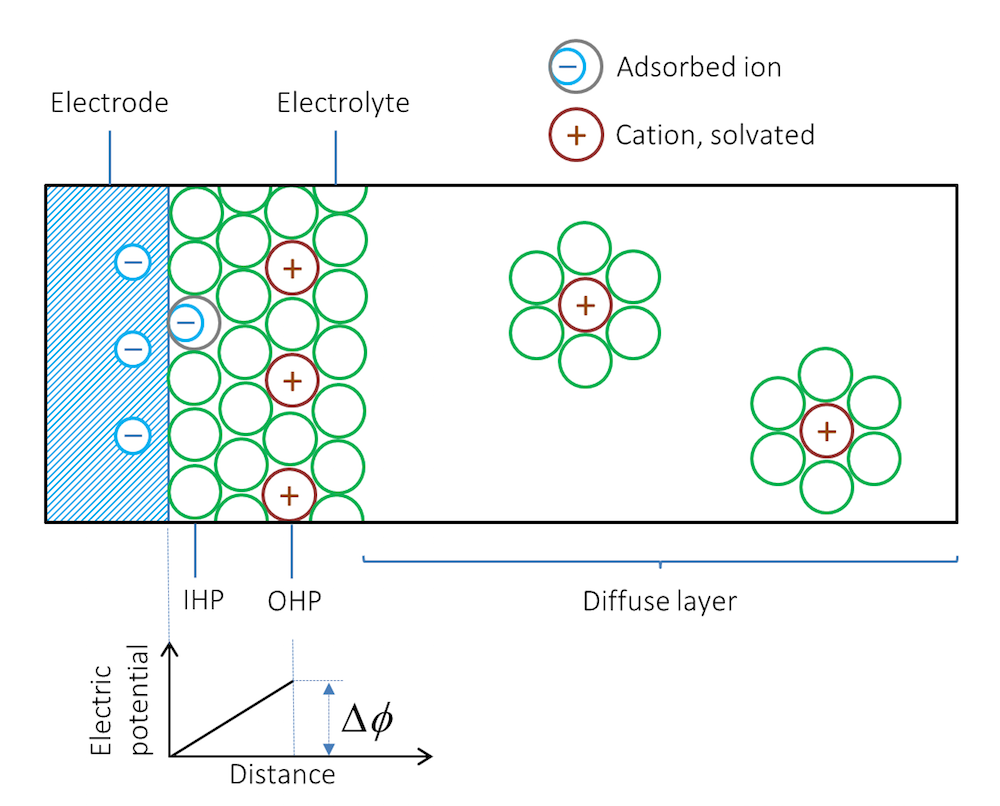
図 2. 電気二重層の模式図. 緑色の円は溶媒分子を表します. 溶媒分子は電気二重層の右側のどこにでもありますが, 溶媒和イオンの周りにのみ描かれています.
金属表面とイオン層が電荷二重層を形成します. 電荷二重層全体の電位差 ΔΦ は, 電流がまったく流れなくても生成されます.
金属によって電子を保持する親和力が異なり, その結果, 異なる電荷のイオンを引き付けます. これは, 電流がない場合の電荷二重層全体の電位が, 同じ電解質内の異なる金属ごとに異なることも意味します.
2つの異なる金属でできた2つの金属ストリップを同じ電解質に浸し, 電流が流れないように高インピーダンス電圧計で電位を測定すると, 2つのストリップ間に電位差が生じます. 金属ストリップ, 電荷二重層 (DL), および金属ストリップ間の電解質全体の電位プロファイルの概略図は, 図 3 に示されています. 高インピーダンス電圧計は, ここでは円で表されています.
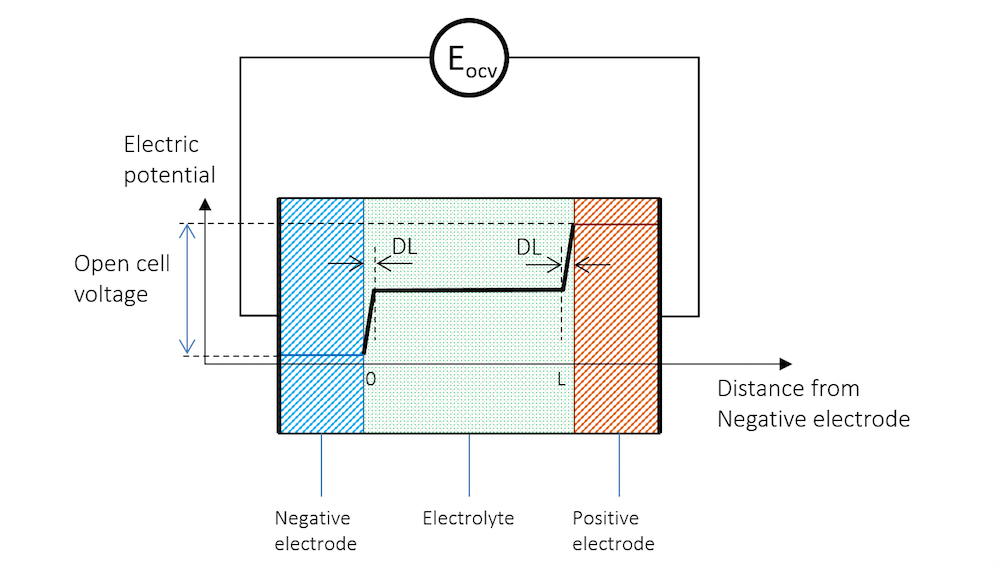
図 3. 負極, 電解質, および高インピーダンス電圧計に接続され, 開放セル電圧 (OCV) を測定する正極間の電位プロファイル.
2つの金属ストリップが, この小さな電池の電極を形成します. 貴金属のほうが正の電位を持ち, 貴金属のほうが負の電位を持ちます.
図 3 では, 2つの電極間の電位差は, 系内で電流が流れないようにするために必要な正確な量です. 平衡状態で正味電流がない場合のセル電圧は, 開放セル電圧 (OCV) と呼ばれ, 図 3 では EOCV で示されています.
このような電池の1つの例は, 亜鉛金属ストリップ (貴金属の少ない金属) と銅ストリップ (貴金属の多い金属) で作られた電池です. 陽極反応は亜鉛の溶解であり, 陰極反応は陽子の水素への還元です. このチュートリアルモデルに示すように, 2つの金属ストリップをオレンジに差し込むだけで, このような電池を作成できます. オレンジジュースが電解質として機能します.
電極の平衡電位を測定することはほとんど不可能であることに注意してください. その理由は, 別の電極の電位を測定するために電解質に測定電極を差し込むとすぐに, 測定電極に帯電二重層が形成されるからです. したがって, 電極電位は常に, 高インピーダンス電圧計を介して接続された参照電極に対して測定されます. 高インピーダンスにより, 測定電極に電位を変化させる電流が流れないことが保証されます.
参照電極の存在は, 図 4 に示されています. 参照電極に対して測定された正味電流ゼロの電極電位は通常, 平衡電位と呼ばれ, 図 4 では Ee,vs Ref と示されています. 図 4 の参照電極と高インピーダンス電圧計は, 負極の平衡電位を測定することに注意してください.
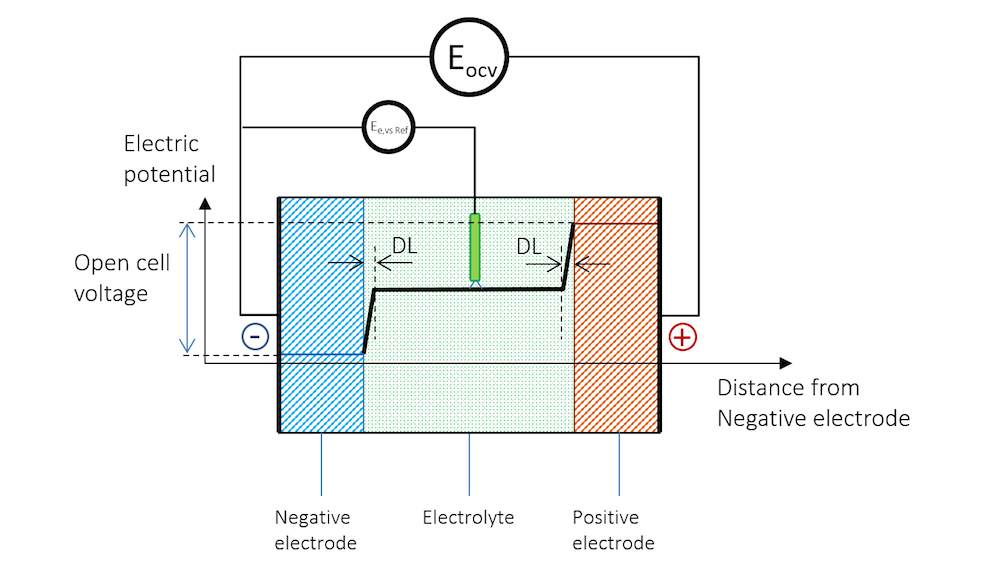
図 4. 電解質に浸された参照電極の表面にも電気二重層が形成され, 測定された電極電位に影響を与えます.
放電中の電位
これで, 外部回路の負荷に2つの金属ストリップ電極を接続できます. 図 5 を参照してください. ここでは, 電流コレクターと電流フィーダーが, 電極の高さ全体に電流を均一に完全に分配できると想定しています. したがって, 電位も電池電極の高さに沿って一定であり, セルの厚さ (負極からの距離) に沿ってのみ変化します.
負荷に2つの電極を接続すると, 負極の電位が上昇し, 電気二重層全体の電位差が減少します. 電位が正になるほど, 金属陽イオンが電解質に放電され, 陽極反応で電子が外部回路に放出されます. この小さな電池では, 陽極反応は次のように表すことができます:
正極では, 電位が正より小さくなり, 陰極反応で放出された電子を受け取ることができる可能性のある正に帯電したイオンがより多く引き寄せられます. また, この場合, 電気二重層全体の電位差は減少します. 私たちの電池では, 貴金属ストリップでのカソード反応は水素発生である可能性があり, その最初のステップでは吸着水素原子の形成が関与する可能性があります:
図 5 は, OCV と放電の間の電位の変化と, 放電中に電池のセル電圧が低下する理由を図式的に説明しています.
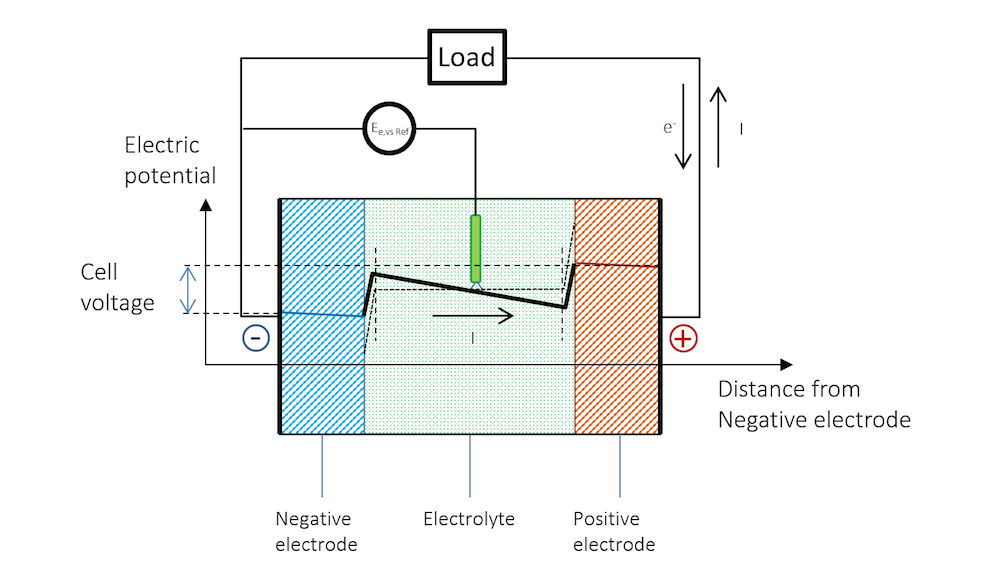
図 5. 放電中の電池全体の電位. 抵抗降下により, 金属ストリップ (青と赤の線) の電位に傾斜があることに注意してください. 金属では, 電流は電子によって伝導されますが, 定義上, 電流とは逆方向に流れることに注意してください. 他の材料では, 電荷キャリアは負または正になります. 慣例により, 電流は常に正電荷の方向に流れるものと想定され, 伝導の材料とメカニズムは考慮されません.
基準電極は, 放電中も溶液に対する電位を維持します. これは, 基準電極に電流が流れていないためです. つまり, 基準電極は分極していません. したがって, 基準電極を使用して, 2つの金属ストリップ電極の分極を個別に測定できます. このような測定では, 金属ストリップの厚さに沿った抵抗損失も取得します. これらの損失は, 青線と赤線のわずかな傾斜で確認でき, 参照電極が中央に配置されている場合は, 電解質の抵抗損失の半分になります.
図 5 は, 金属および電荷二重層の外側の電解質内の電流の流れが純粋にオーム性である可能性があることを示していますが, 多くの電池電解質では拡散が寄与する可能性があります. 電流は電気二重層の外側で正電位から負電位に流れます.
電池やその他の電気化学セルをモデル化する場合, 電気二重層全体の電位プロファイルは, 通常はミリメートルスケールである電極と電解質と比較して, ナノメートルスケールの非常に薄い領域に限定されます. このため, 数学的モデル化では, 電気二重層は不連続として扱われます. 電解質内の電位は, 通常 Φl と表記される1つの従属変数でモデル化され, 金属電極内の電位は, 通常 Φs と表記される2番目の従属変数でモデル化されます. 電気二重層を横切る電位差は, ΔΦ = Φs – Φl と定義されます.
電荷移動反応, 電荷移動電流, および過電位
電流がない場合と電流がある場合の充電された二重層上の電位の差は, 過電位と呼ばれます. 繰り返しますが, 電荷二重層は参照電極を基準としてのみ測定できるため, 過電位 η も参照電極を基準として測定されます.
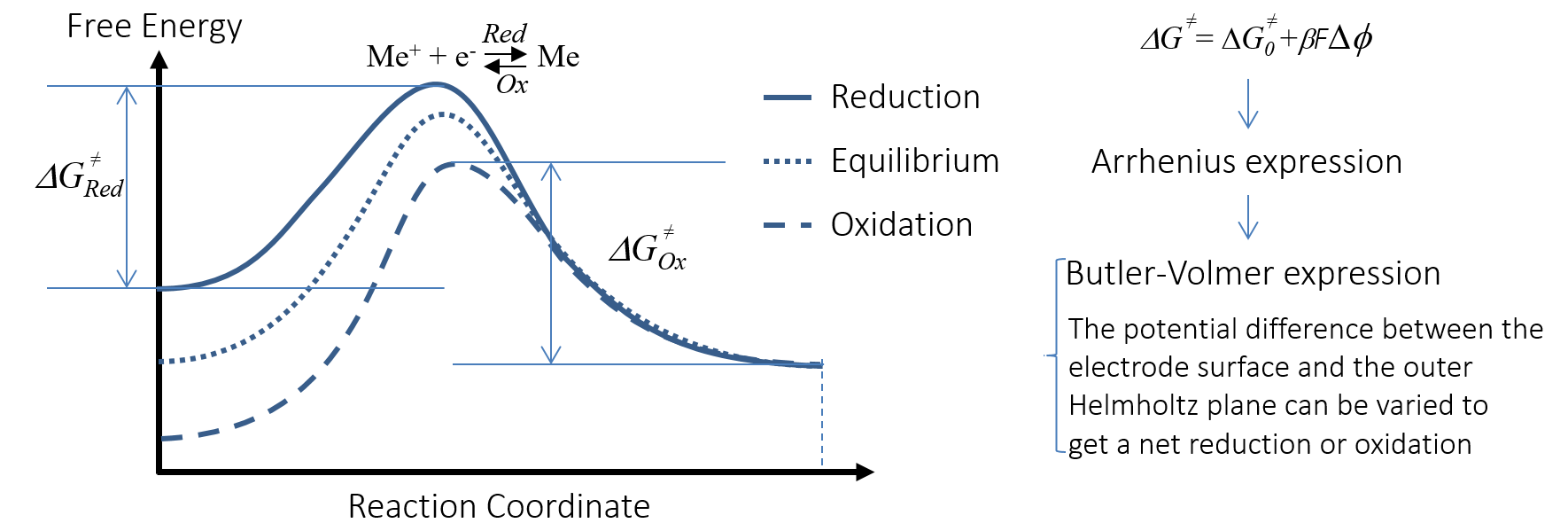
過電位は, 電荷移動反応, つまり陽極酸化反応と陰極還元反応の活性化エネルギーを変えることができます. これは, 陽極酸化されて Me+ になる金属 Me の 図 6 で視覚化されています. 活性化エネルギープロットの x 軸は, 負極の酸化還元反応の反応座標です. プロットは, 自由エネルギーと二重層の電位差 ΔΦ を相関させます.
図 6. 電荷移動反応の活性化エネルギーは電気二重層の電位差によって変化し, 電荷移動反応を加速または減速します.
陽極酸化は, 負極の電位を上昇させることで加速され, 二重層全体の (負の) 電位差がいくらか減少します. グラフでは, 電位によって帯電種の自由エネルギーが変化します. 電荷移動反応は, このようにして, 陽極として機能する金属ストリップから電子を “取り”, 金属イオンを電解質に送り込みます. 電子は外部回路を通って負荷を介して正極に流れます. 図 5 を参照してください. 電解質内のイオンは電界内を移動し, 電解質内の電流を正極に運びます. これも 図 5 に示されています.
図 5 と 図 6 に示されているプロセスは, 電位の関数として電荷移動反応で移動した電子の測定値である電荷移動電流密度 ict を示すプロットで表すことができます. これは 図 7 に示されています. 2つの曲線は, 電位の関数として電解質と金属の界面上の電荷移動電流密度を示しています. 負極の曲線は青で, 正極の曲線は赤です.
放電中, 負極は陽極過電圧 ηa で値 ict,a の陽極電流密度を取得します. つまり, 電極は正に分極されます. これは, 上記の 図 5 とも一致しています. 電位差 ΔΦ は小さな負の値ですが, 平衡時の同じ差はより大きな負の値であり, 結果として正の過電圧になります. 陽極電流は, 定義により正の電流です.
正極は負に分極し, 定義により負の陰極電流になります. この場合, 金属ストリップの面積 (キルヒホッフ数) が同じであれば, 電流の値は陽極電流密度と反対の符号を持ちますが, 絶対値は同じです. 対応する陰極過電圧は ηc です. 質量輸送の制限がない場合, Butler-Volmer 方程式は 図 7 の赤と青の曲線を記述できます.
図 5 と同様に, 図 7 も, 図 3 の開放セル電圧と比較して, 放電時にセル電圧 Ecell が減少する理由を説明しています. 電位の一部は抵抗損失でも失われますが, この損失はプロットには含まれていないため, 実際にはこの図で示されているよりも少し減少する可能性があります.
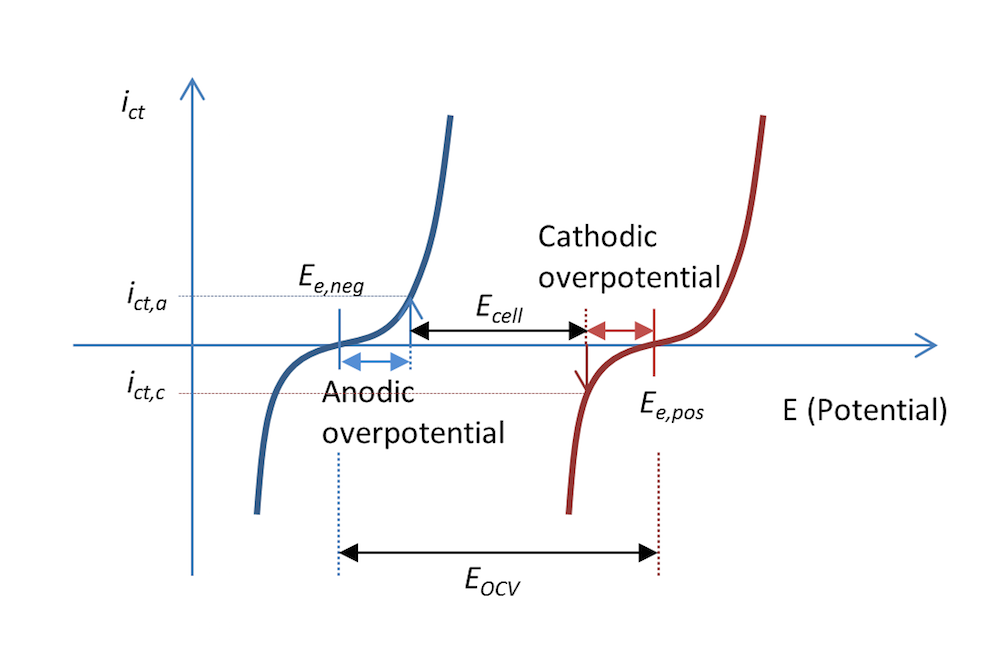
図 7. 放電中の小さな金属ストリップ電池の負極と正極の電極電位の関数としての電荷移動電流密度. この場合, 放電電流密度は abs(ict,c) = ict,a です.
電池の再充電
ここで, 金属ストリップ電池を再充電するとします. これには電荷移動反応を逆転させる必要があり, 負極でカソード電荷移動反応が発生し, 正極でアノード電荷移動反応が発生します.
図 8 は, 再充電を行うには負極をより負にする必要があることを示しています. これにより, 電荷二重層上の電位が上昇します. これは, 図 6 に示すように, 純還元反応に対応します. 負極は, 負の電荷移動電流密度を持つカソードになります. カソード還元反応は次のようになります.
正極をより正にする必要があります. これにより, 電荷二重層上の電位も上昇します. これは, 電池の純酸化反応に対応します. 正極は, 正の電荷移動電流密度を持つアノードになります. 水性電解質およびより “貴な” 金属ストリップの場合, これは通常, 水酸化物イオンの酸化になります. 最初のステップでは, この酸化は陽極表面でのヒドロキシルの吸着を伴う可能性があります:
2番目のステップでは, 水と酸素が生成されます. より貴な金属の場合, 金属イオンを溶液に放出するにはさらに高い電位が必要になります. したがって, 水電解質の一般的な反応は, まず水酸化物イオンを酸化するか, 水を分解して酸素を形成することです.
図 8 は, 電池の再充電に開放セル電圧よりも高い電圧が必要な理由を説明しています.
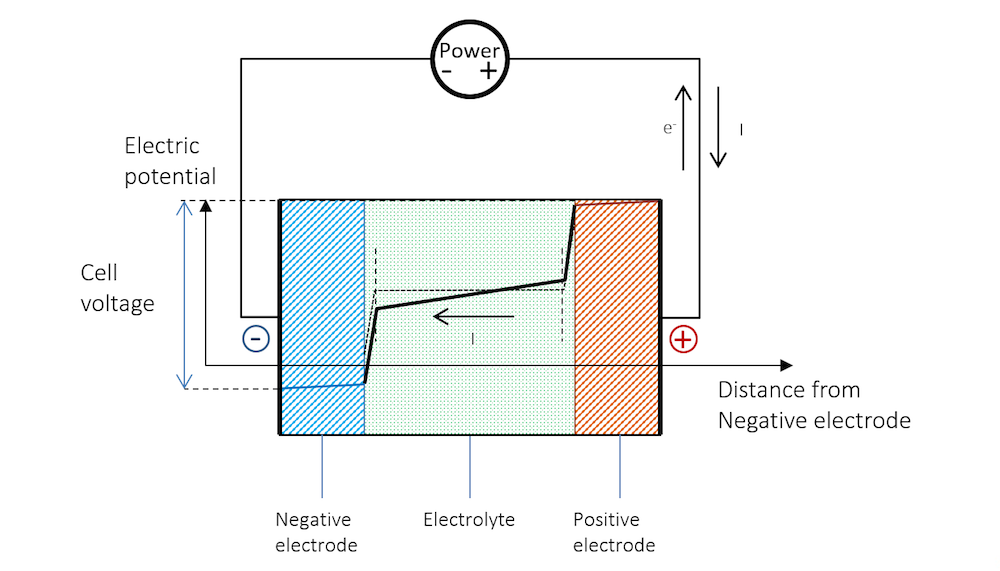
図 8. 充電中の電池全体の電位. ここでは, 放電中と同様に, 抵抗降下により金属ストリップ (青と赤の線) の電位に傾斜があることに注意してください.
2つの金属電極表面での電荷移動反応による電流密度は, 図 9 に示されています. 負極は負に分極され, 定義上負であるカソード電流が発生します. 正極はさらに正になります. つまり, 正に分極され, 正の陽極電流が得られます. この図は, 必要な陽極電流と陰極電流を流すために, 充電中に電池全体の電圧が開放セル電圧よりも大きくなければならない理由も説明しています.
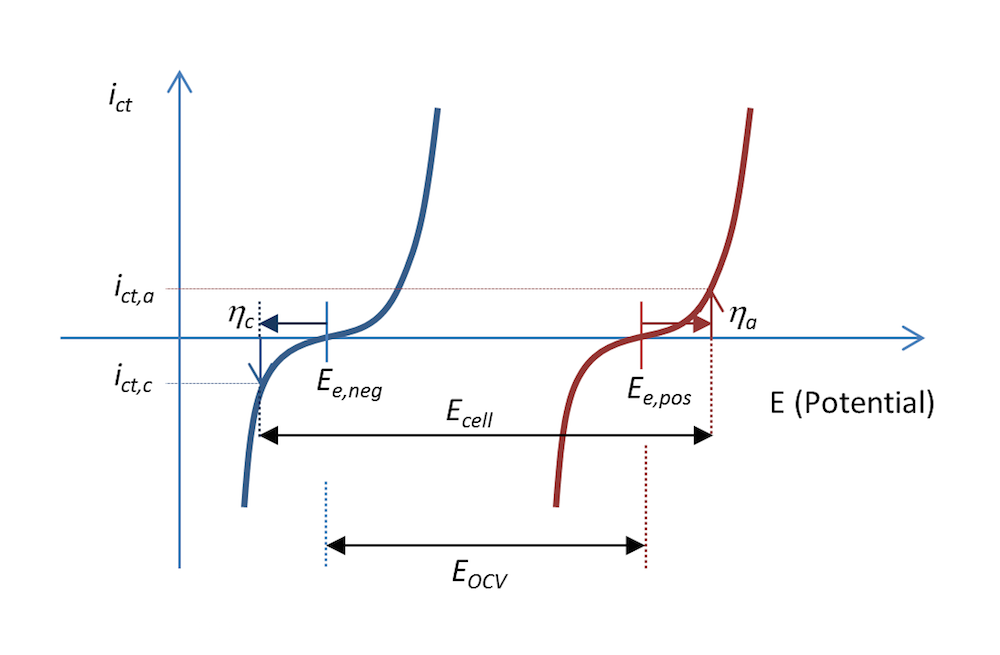
図 9. 充電中の小さな金属ストリップ電池の負極と正極の電極電位の関数としての電荷移動電流密度 (電流密度 ict).
多孔質電極
ほとんどの電池では, 固体の金属ストリップではなく多孔質電極が電極として使用されます. これにより, 電気化学反応のための表面積が大幅に拡大し, 電池が “コンパクト” になり, 電気出力に対して重量が軽いユニットになります. これらの電池では, 電極の細孔に電解質が含まれており, これを細孔電解質と呼びます. 充電された電荷二重層は, 細孔電解質と接触している細孔壁の周囲全体に形成されるため, 表面積が増加し, 局所的な電荷移動電流密度が減少し, 放電および再充電中の過電圧損失も減少します.
図 10 は, 多孔質電極を備えた電池の開放セル電圧での電位分布を示しています. 電解質電位は, 自由電解質と細孔電解質の両方で定義されます.
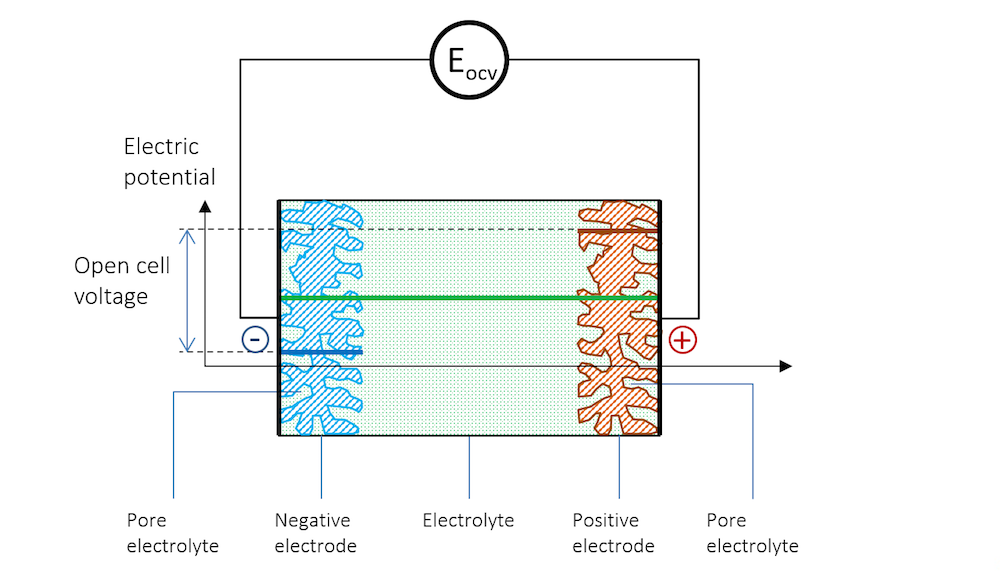
図 10. 多孔質電極を備えた電池の電解質, 細孔電解質, および多孔質金属の電位プロファイル.
電池を放電すると, 電流が電極材料から負極の細孔電解質に流れ込みます. つまり, 図 11 に示すように, 多孔質負極の電流フィーダーから電極間の自由電解質に面するエッジまで, x 軸に沿って左から右に進むにつれて, 細孔電解質の純粋なオーム電流密度が増加します.
平均電流密度は x の関数として一定ではないため, 細孔電解質の電位プロファイルは一定の傾きの線ではありません. 電位プロファイルの曲率は 図 11 に示されています. 負極の細孔電解質では, 電解質電位の勾配 (緑) は x とともに増加します. 多孔質金属の電位の勾配 (青の曲線) は x とともに減少します. これは, 電荷移動反応で電流が x 軸に沿って電解質に移動するからです.
正極では, 逆のプロセスが起こります. 自由電解質に面する端の勾配は, 細孔電解質の電位 (緑) で最大になり, x とともに減少します. これは, 電流が正極の細孔電解質から多孔質金属に移動するからです. 多孔質金属の電位の勾配 (赤) は, より多くの電流が細孔電解質から移動するにつれて, x とともに増加します. 集電体の位置では, すべての電流が金属に流れます.
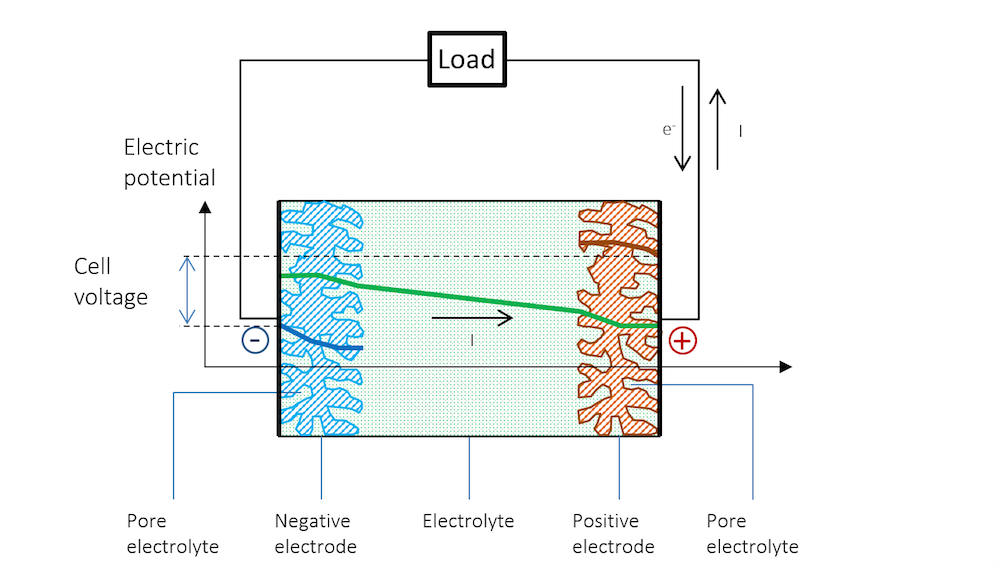
図 11. 放電中の多孔質電極付き電池の電位プロファイル.
電池内部の電流流れに関する結論
この議論は些細なことに聞こえるかもしれませんが, 上記の原理を理解することは, 電気化学の概念を理解するための最も重要な要件の1つです. この理解を得るには, ある程度の読書と実践的なモデリングおよびシミュレーション作業が必要です. 学校の先生がこの概念を説明するのに苦労したのも不思議ではありません.
追加資料
- Orange Battery tutorial model
- 1D Isothermal Lithium-Ion Battery tutorial model
- J. O’M. Bockris and A. K. N. Reddy, Modern Electrochemistry Volume 2, Springer-Verlag, 1970.
- J. Newman and K. E. Thomas-Alyea, Electrochemical Systems 3rd Edition, Wiley, 2004.
編集者注, 2020年2月13日: 読者の要望に応じて, このブログに付随するモデルファイルをアプリケーションギャラリのエントリ, 電池および電気化学セルの電位プロファイル にアップロードしました.



コメント (0)