このブログでは, 状態変数と呼ばれる COMSOL Multiphysics® ソフトウェアの強力なツールについて説明します. 有名なマンデルブロ集合やいわゆるフラクタルノイズなど, フラクタルを生成するためにそれらを使用する方法を学びます. フラクタルの生成は, 状態変数の最も一般的な用途ではありません. とはいえ, このブログは, 状態変数, 複雑な算術演算, および乱数の使用について詳しく学ぶための有益で洞察に満ちた楽しい方法です.
フラクタルとは?
大まかに言えば, フラクタルは, さまざまなスケールで何らかの形の自己相似性を示すオブジェクトです. これはかなり抽象的に聞こえるかもしれませんが, フラクタルパターンは実際に自然界に存在します. あなたはそれについて考えるかどうかにかかわらず, 自分でそれらに遭遇したことがあります.
たとえば, シダはフラクタルパターンを示します. 下の図に示されている各シダの葉は, 小さな枝または pinnae と呼ばれる下位区分で構成されており, 主要な茎に沿って成長し, 主要な葉自体と同様のパターンを示します. 個々の耳介は, さらに小さな部分 (pinnules) で構成されており, 一部のシダではさらに小さな部分に細分化される場合があります.

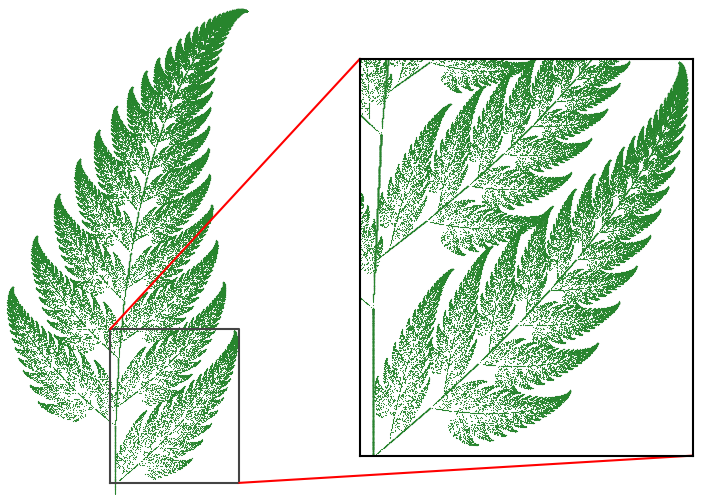
本物のシダの葉とコンピューターで生成されたバーンズリーシダ.
バーンズリーシダという, 自然界に見られるパターンに触発された数学的な対応物があります. このシダの葉の数学的表現は, 数行のコードしか必要としない反復関数を使用してコンピューター上で生成できます. 結果の画像はシダの葉に似ており, 現実世界のインスピレーションと同様に, メインの葉自体と同様の形状のサブディビジョンで構成されています. 実際, バーンズリーのシダは, より小さな自己相似形に無限に細分化しますが, 本物のシダの自己相似性は, 数レベルしか保持されません.
以前のブログで説明したように, フラクタルはその魅力的な外観に加えて, 実際にはさまざまな現実世界での用途があります. 別のアプリケーションは, コンピューターゲームのように, 風景, 雲, 木, または他の植物などの自然に見えるオブジェクトを模倣するコンピューター生成画像です. このブログの後半で, フラクタルパターンを使用してややリアルな風景を生成する方法を紹介します.
マンデルブロ集合
おそらく最も有名なフラクタルの1つは, マンデルブロ集合です. つまり, 単純な反復関数によって生成される複素数の集合です. 複素数 c は, 特定の反復関数と絶対値 || z_\textrm{n} || に組み込まれている場合, 集合の一部と見なされます. || z_\textrm{n} ||は何度も反復しても発散しません. 数値がセットの一部であるかどうかを確認するには, 単純に次の式に代入します:
たとえば, 数値 c=1+0.25 i を試してみましょう. 最初の反復は z_1=1+0.25 i (|| z_\textrm{n} ||=1.03) を生成します. 2番目の z_2=1.94+0.75 i (|| z_\textrm{n} ||=2.08), 3番目の z_3=4.19+3.16 i (|| z_\textrm{n} ||=5.25) など. この場合, 絶対値 || z_\textrm{n} || は発散しているように見えるため, 1+0.25 i はマンデルブロ集合の一部ではありません.
COMSOL Multiphysics® でマンデルブロ集合を計算
COMSOL Multiphysics でマンデルブロ集合を計算するのは, 実際には非常に簡単です. そのために, 複雑な平面として解釈する 2D ジオメトリを作成します. この平面の各点 (x,y) は, 反復にプラグインできる複素数 c=x+i y を表します. 次の数値 z_\textrm{n+1} を計算するには, 前の結果 z_\textrm{n} を追跡する必要があります .
前の計算ステップからのデータを追跡する状況に直面したとき, 状態変数機能は便利なツールです. 状態変数機能では, 必要な数の変数を定義できます. この場合, zn と aura という2つの変数を定義します.
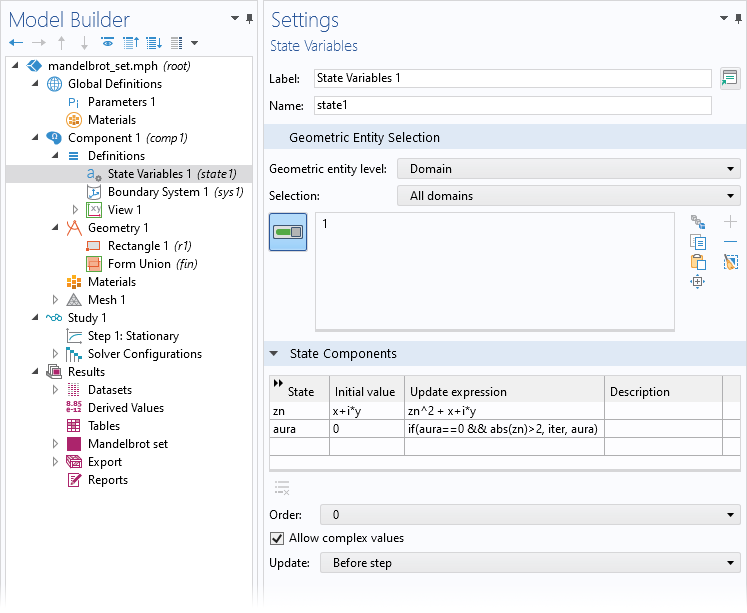
状態変数の定義.
最初の状態変数は, 任意の反復ステップおよび複素平面内の任意のポイントでの z_\textrm{n} の現在の値を追跡します. 初期値列で zn を初期化します. 更新式は反復関数で, 前の反復の結果 zn を2乗してから c=x+i y を追加します. aura という2番目の状態変数も追加しました. 場をゼロで初期化し, zn の絶対値が2より大きくなるまで必要な反復回数を格納します.
いくつかの反復ステップ中で z_\textrm{n} の場合, || z_\textrm{n} || > 2 が最終的に発散することを示すことができます. これらの関数を数回反復して解いて結果をプロットすると, マンデルブロ集合が現れることがわかります.
マンデルブロ集合と, 25回の反復で計算された, その aura.
黒灰色の形状は, マンデルブロ集合 (変数 zn) の一部である複素数を表します. 各反復で, 実際に集合の一部である数値のより近い近似値を取得します. 灰色のさまざまな色合いは, zn の絶対値を示します. 一部の初期値 c では, 反復関数は単一の値に収束しませんが, 代わりに異なる値の間でジャンプします. アニメーションでは, 光源がオンとオフを繰り返します. マンデルブロ集合の外側にある色付きの場は aura を表し, 数字がどれだけ速く発散するかを示します. マンデルブロ集合の境界に近づくほど, 絶対値が2を超えるまでに必要な反復回数が増えます.

c \approx -0.7789333 + 0.1345 \, i 300回の反復で計算された中心位置のらせん構造. 画像の幅は 0.01 で, 高さは 0.00666 です.
フラクタルノイズ
フラクタルと状態変数の要点を理解したところで, コンピューター生成画像の分野におけるフラクタルのより実用的なアプリケーションを見てみましょう. より具体的には, いわゆるフラクタルノイズを使用して有機的に見えるテクスチャをエミュレートする方法を見ていきます. 後で説明するように, この手法は実際に COMSOL Multiphysics で使用され, さまざまな材料のリアルな可視化を実現します. フラクタルノイズのもう1つの一般的な用途は, コンピューターゲームで自然に見える地形を手続き的に生成することです.
ノイズを使って人工的な風景を作りましょう. ここで説明するコンテキストでは, ノイズはランダムな値であると理解しています. つまり, 引数として2つの座標を取り, 疑似乱数を返す関数, たとえば noise(x, y) を探しています. 結果は, 指定された位置での地形の高さとして解釈されます. COMSOL Multiphysics のランダム関数を使用すると, いわゆる, ホワイトノイズを作成できます. 結果を xy 平面にプロットすると, 数値はある座標から次の増分にランダムかつ独立してジャンプします. 明らかに, これは現実世界で見られる風景のようには見えないため, より良いアプローチが必要です.

一様分布のホワイトノイズ. 値は最小値と最大値の間でランダムにジャンプします.
パーリンノイズ
代わりに, ランダムな値を生成するノイズ関数を探していますが, 同時に “あまりにもランダム” ではなく, むしろ自然に見えるべきです. 隣接するポイント間にある程度の一貫性があるはずです. パーリンノイズは, Ken Perlin によって開発されたもので, 疑似乱数値を生成できる特別な形式のノイズです. 与えられた座標に対して, ある点から隣接する点へのノイズ値の遷移は滑らかです. この “滑らかなランダム性” は, 自然界に見られるパターンのように見えます.
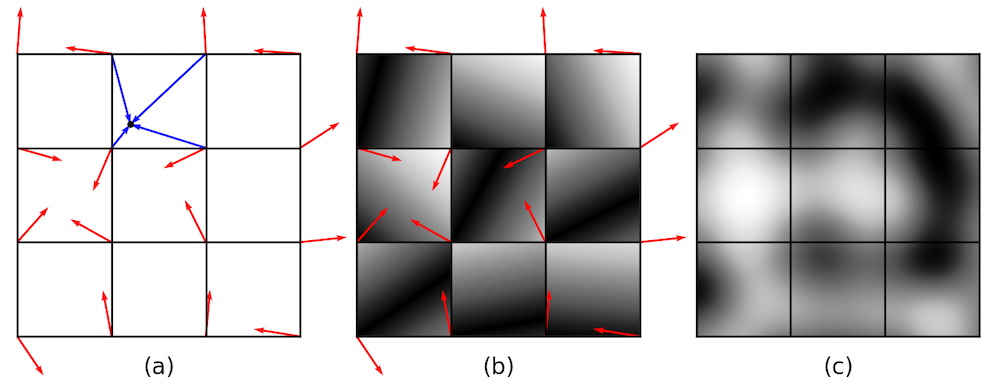
2D パーリンノイズの生成: (a) グリッド定義. 赤い矢印は, ランダムに生成された勾配ベクトルです (見やすくするために 0.5 倍にスケーリングされています). 青い矢印は, 周囲のグリッドポイントから特定の位置 (x, y) を指しています. (b) 左下の勾配ベクトルを使用した最初の内積の絶対値. グレースケールは, 0 (黒) と 1 (白) の間の値を示します. (c) 補間ノイズ.
パーリンノイズの生成には, 上で概説したいくつかの手順が含まれます. 最初のステップでは, xy 平面を単位正方形のグリッドに分割します. 各グリッドポイントで, 勾配ベクトル (赤い矢印) とも呼ばれる長さ1の疑似乱数ベクトルを生成します. ポイント (x,y) に関連付けられた周囲の4つの勾配ベクトルは疑似乱数にすぎません. 同じポイントでノイズを再計算すると, 常に同じになるはずだからです. 勾配ベクトルを使用して, 平面内の任意の場所にあるポイント (x,y) のノイズ値の計算を開始できます. この特定の点について, 勾配ベクトル間の4つの内積を計算し, グリッドポイントから選択した点 (x,y) 自体 (青い矢印) を指す位置ベクトルを計算します.
4つの内積は, 勾配が選択したポイントのノイズレベルに与える影響として解釈できます. 勾配ベクトル \mathbf g_\textrm{i} と位置ベクトル \mathbf x – \mathbf x_\textrm{gi} の間のドット積は, 両方のベクトルが同じ方向を向いている場合に最大値に達し, 互いに垂直である場合に最小値に達します. パーリンノイズを生成する最後の手順は, 4つの内積の加重平均を計算し, 補間値を返すことです. これには, 巧妙に選択された平滑化されたステップ関数と線形補間が含まれます. これにより, ドメイン全体でスムーズな遷移が得られます. パーリンノイズの計算方法の詳細については, 参考文献1を参照してください.
フラクタルノイズ
私たちが生成したパーリンノイズは, 非常に滑らかな遷移を持っており, 実際の地形のようには見えない可能性があります. 通常, 丘や小さな岩など, より局所的な不規則性が見られます. 解決策は, さまざまなオクターブのノイズを重ね合わせることです. ここで, フラクタルのアイデアが役立ちます. 基本的には, 周波数が高いほどノイズが多く発生します. つまり, 同じ距離で山と谷が多くなります. 音楽のように, 周波数はオクターブごとに2倍になります. 高周波ノイズの振幅を減らし, それをベースノイズに追加します. 原則として, ノイズのオクターブは好きなだけ追加できます. そのため, noise() 関数を1回だけ呼び出すのではなく, 複数回呼び出して, 調整された振幅で結果を合計します.
h を景色の高さとして解釈すると, 最初の反復 (j=0) で, 山などの大きくて明確な特徴を持つ地形の最初の滑らかな概算が得られます. 2番目の反復は, より局所的な丘やくぼみからのものかもしれません. 3番目の繰り返しは, 個々の岩や岩層からのものかもしれません.
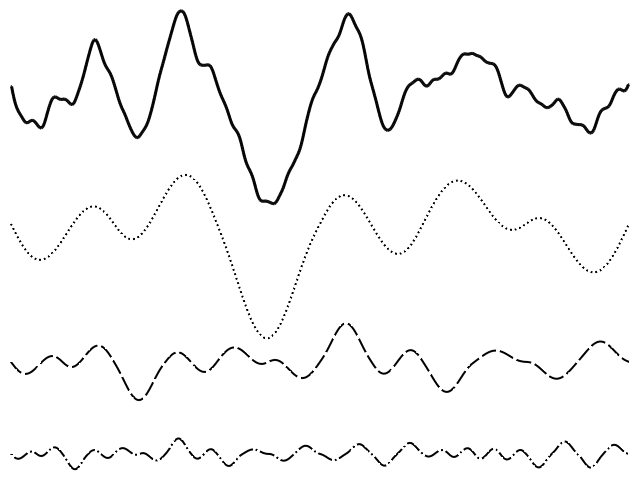
1D フラクタルノイズ (上の線). 以下は, パーリンノイズの最初の3つの周波数であり, これらを合計すると, 上部の線が形成されます.
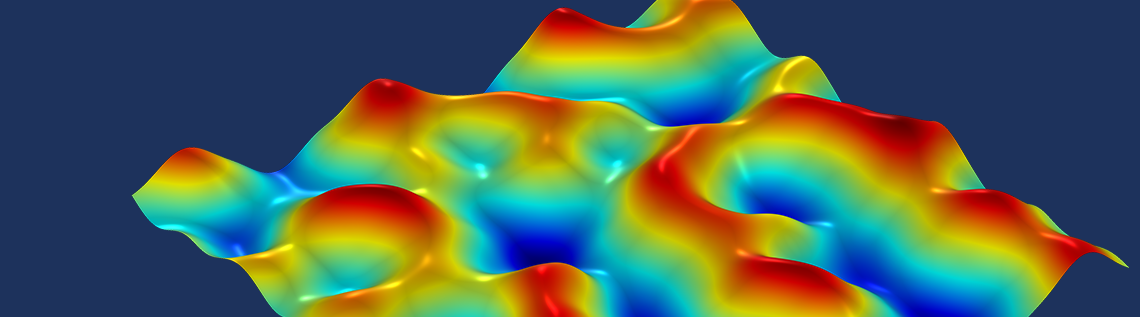
フラクタルノイズの生成には, 異なる周波数のノイズの計算と重ね合わせが含まれます. COMSOL Multiphysics でこれを行う場合, 以前のすべての周波数から結合されたノイズを記憶したいので, 状態変数を利用すると便利です. 次のアニメーションは 2D 高さマップを表しており, ベースノイズに追加される高周波数ノイズのレベルごとに, 地形の詳細がますます明らかになります.
パーリンノイズの5つの周波数を重ね合わせて生成された地形図. 等高線と異なる色は異なる高さを表します.
ランダム化された表面ジオメトリは, 物理シミュレーションのコンテキストで使用できます. たとえば, 表面の粗さや不均一な材料をモデル化する必要があります. 以前のブログで, 三角関数をさまざまな振幅と周波数, および画像またはテキストファイルから任意のジオメトリを作成する方法を紹介しました.
ノイズによる素材感の向上
プロットにフラクタルノイズを追加して, COMSOL Multiphysics の素材の外観を改善できることを知っていますか? バージョン 5.6 以降, 素材用の特別な可視化オプションがあります. さびた鋼, 革, 水などの一部のビルトイン材料タイプは, シンプレックスノイズを使用して よりリアルなテクスチャを作成します. シンプレックスノイズはパーリンノイズと類似しており, Ken Perlin によって開発されました. 必要な効果を得るために, ノイズパラメーターを自分で微調整することができます.
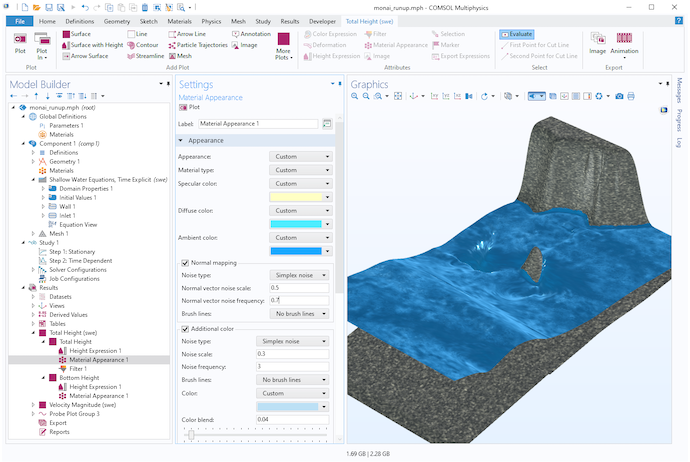
浅水方程式モデルでシンプレックスノイズを使用した水の可視化.
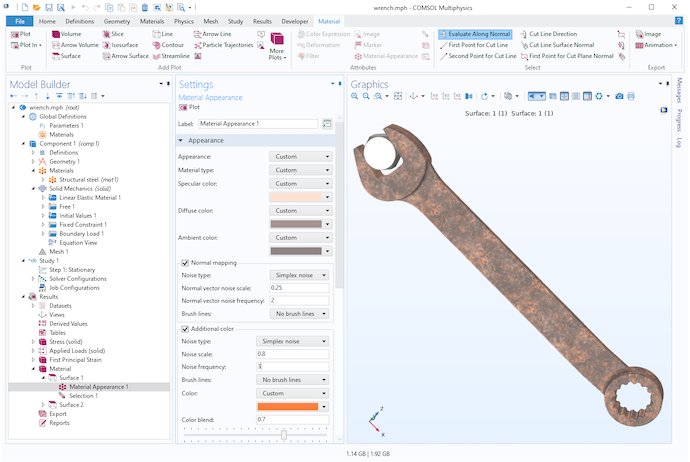
レンチモデルのさびたスチール表面のシンプレックスノイズを使用した可視化.
自分で試す
このブログで説明されているマンデルブロ集合またはパーリンノイズのモデル化を試してみませんか? MPH ファイルにアクセスするには, 下のボタンをクリックしてください.
参考文献
- K. Perlin, “Improving Noise”, New York University, 2002. https://mrl.cs.nyu.edu/~perlin/paper445.pdf.
その他の参考文献
フラクタル, ノイズ, 状態変数については, 次の関連ブログも御覧ください.


コメント (0)