三相送電線の損失

ある同僚が, 三相送電の損失について興味深い質問を投げかけました. 送電線における導体のある種の幾何学的配置は, 構造が対称に見えても, 電線間の損失の不均衡をもたらすことがわかりました. このことを実証するために簡単なモデルを作り, 今日はこの直感に反する結果を検証する方法を説明します.

不均衡な損失, しかしその理由は？

同じ銅線が3本, 等間隔で水平に並んでいて, 三相電力を運んでいるとしましょう. それぞれの電線の損失はどうなるでしょうか？この状況を左の回路図に示します. 電線は非常に長く, 断面が一定であると仮定し, モデルを2次元断面モデルに縮小し, 周波数領域で解きました.

COMSOL Multiphysics^® ソフトウェアで, コイル ドメイン条件と複素数による電流定義（互いに120度位相がずれた）を使用して各ワイヤーをモデル化しました.

三相送電線のモデリングに関する詳細なチュートリアルについては, ケーブル チュートリアルシリーズ< /a>を参照してください. 3本のワイヤーを通る電流の合計はゼロになるので, 境界に沿って電流が戻る経路を気にする必要はありません. 各ワイヤー内の損失分布を右下の図に示します.

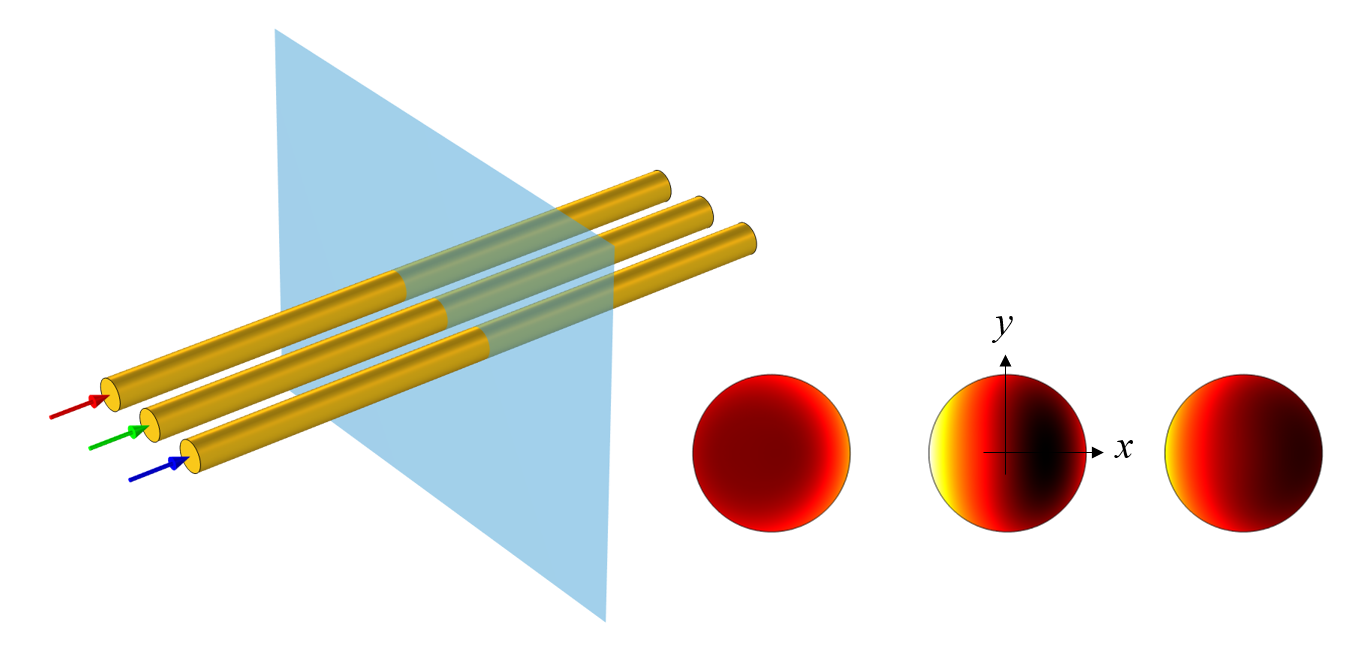
三相電流を流す3本の平行線の回路図と, 断面における損失のプロット.

このプロットでは, 損失分布はx 軸に関して対称ですが, y 軸に関しては対称ではないことがわかります. ジオメトリは両方の軸に関して明らかに対称であるため, これは珍しいように思えるかもしれません. では, この結果はどのように説明できるでしょうか?

バランスの取れた異なるケースから始める

この動作を理解するにはさまざまな方法があります. ここでは, 物事を理解しやすくするために幾何学的な変更を適用することから始め, その後, その理解が私たちをどこに導くのかを見ていきます. 以下の左図に示すように, 導体を正三角形の配置に再配置してみましょう. このケースを解くと, すべての導体が同じ合計損失と同じ損失分布を持つことがわかります. 損失分布が回転対称であることにも注目してください. つまり, 重心の周りでフィールドを 120 度回転すると, 同じ分布が得られます. ここで, 場が対称である理由を理解し, それが元のケースの理解にどのように役立つかを見てみましょう.

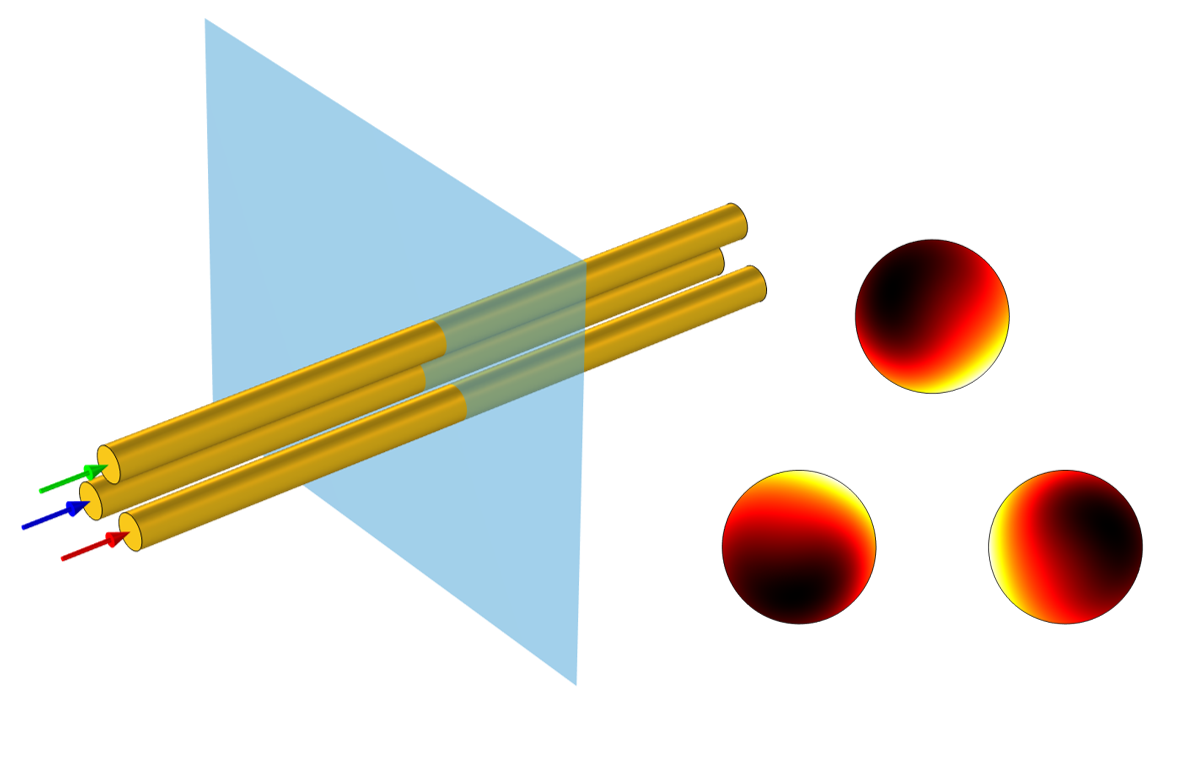
正三角形に配置された 3 本の電線はバランスのとれた損失を示します.

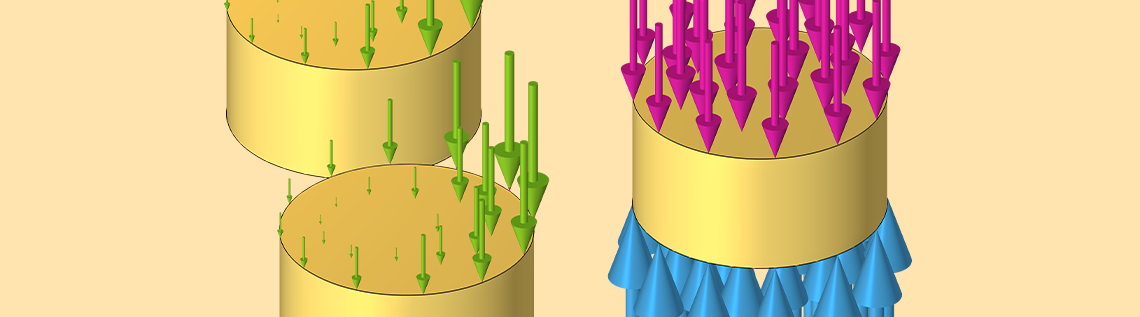
AC 電流が1本の電線を介して駆動されると, 結果として生じる時間変化する磁場によって電線自体内に電流が誘導されます. これらの逆誘導電流は, 特に電線の中心内で駆動電流に逆らう傾向があり, いわゆる 表皮効果 を引き起こします. 電線自体に流れる逆誘導電流に加えて, 近接効果により, 駆動電流が隣接する2本の導線に電流を誘導します. 正式な証明はないものの, 隣接するワイヤーに流れるこれらの誘導電流は以下の通りであると述べておきます:

• 隣り合う2本の導体の大きさと間隔が等しいため, 大きさが同じ.
• 互いに120°位相がずれている.

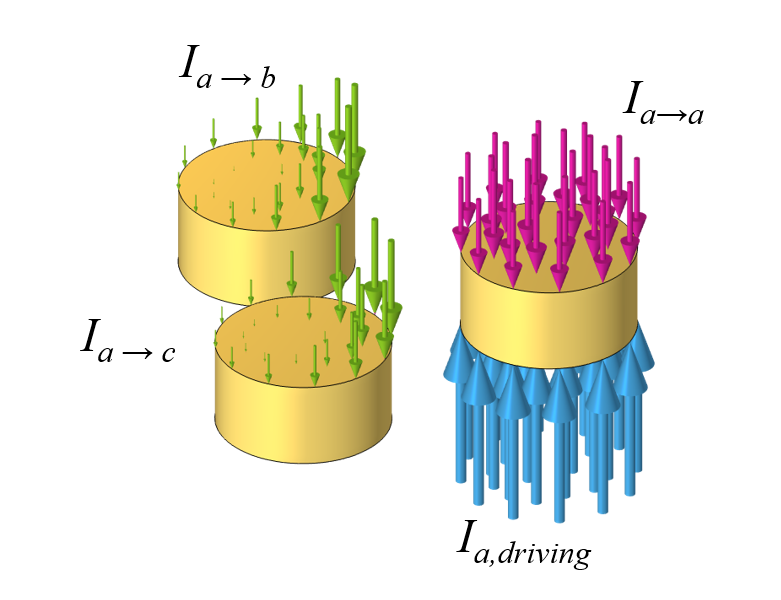
電線の1本に流れる駆動電流だけを見ると, 電線自身と隣接する2本の電線に電流が誘導されます.

三相電流が3本の電線すべてを通して駆動されている場合, これら3本の電線のうちの1本を流れる総電流は, その電線の駆動電流, 逆誘導電流, および隣接する電線からの誘導電流の合計であり, 例えば, I_{a,tot}=I_{a,driving}+I_{a \rightarrow a }+I_{b \rightarrow a}+I_{c｜rightarrow a }となります.三相電流を駆動するために必要な印加電圧は駆動電流に比例し, V_{a}=I_{a,driving} R で与えられます. ここで, R は DC ワイヤー抵抗です.

これらの電流を駆動するためにコイル機能を使用すると, 追加のグローバル方程式が方程式系に追加されます. これにより, 必要な合計電流を誘導する電圧が求められます. 各電線の合計損失は, Q_a = \frac{1}{2} \Re \left( I_{a,tot} V_a \right) で求められます. 電流と電圧は複素数値であり, 互いに 120° 位相がずれています.

次に, これらの電流を複素平面でプロットしてみましょう. これは, これら 3 つの逆誘起電流がどのように合計されて合計電流になるかを可視化するのに役立ちます. これらの項の真の大きさや位相は実際にはわかりませんが, 隣接する 2 本の電線からの誘導電流の位相が互いに 120° ずれていることはわかっています.

また, 電流の相対的な大きさが次のとおりであると合理的に仮定することもできます. |I_{a,driving}| > | I_{a \rightarrow a } | > | I_{a \rightarrow b}| = |I_{a\rightarrow c } |. この情報と仮定により, 以下のスケッチを作成することができました.

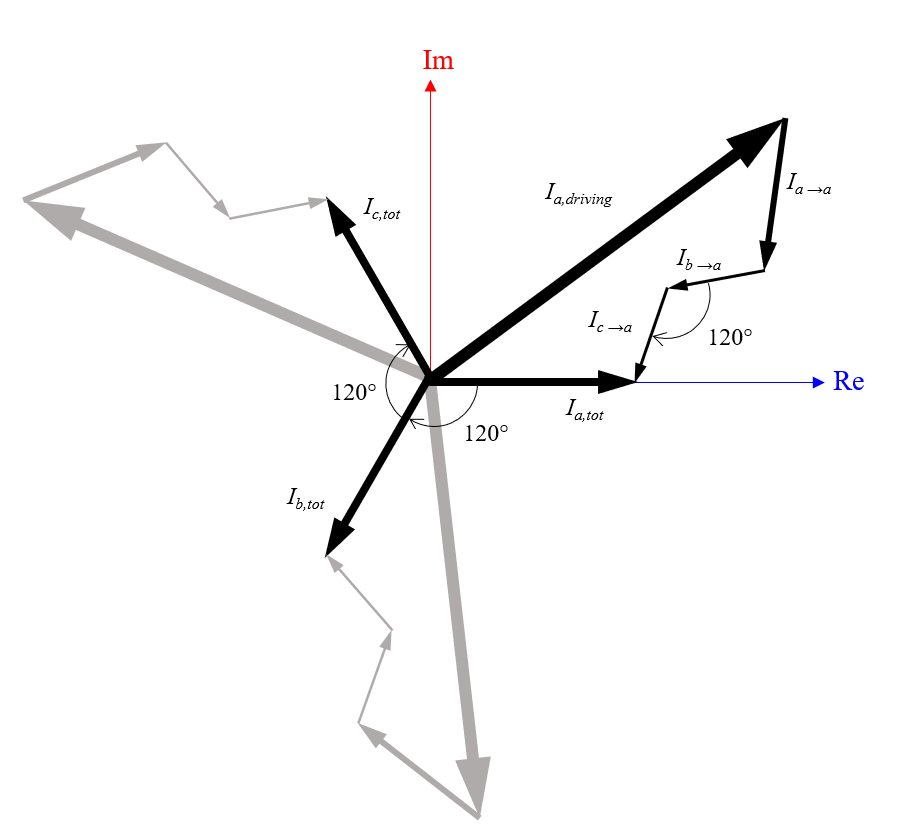
駆動電流, 逆誘導電流, および他の電線から誘導される電流の合計が合計電流となります. 正三角形に配置された同一の電線の場合, これら 3 つの電流は大きさが等しく, 互いに 120° 位相が異なります.

すべての電線に固定された複素数値の駆動電圧を考えて, 電線を等辺配置から直線配置に移動すると何が起こるかを考えてみましょう. 中心の電線に a というラベルを付けます.

逆誘導電流, たとえば I_{a \rightarrow a } は変化せず, 中央の電線から側面の電線への誘導電流の大きさも同じままです. : | I_{a \rightarrow b}| = |I_{a\rightarrow c } |. 一方の電線から中央の電線ともう一方の外側電線への誘導電流は異なります. | I_{b \rightarrow a}| \ne |I_{b\rightarrow c } | と | I_{c \rightarrow a}| \ne |I_{c\rightarrow b } |. ただし, 外側の 2 本の電線間の誘導電流の大きさは同じになります. | I_{b \rightarrow c}| = |I_{c\rightarrow b} | — そして相対位相は一定のままです. 合計をプロットして, 三角形と線形の配置を比較できるようになりました.

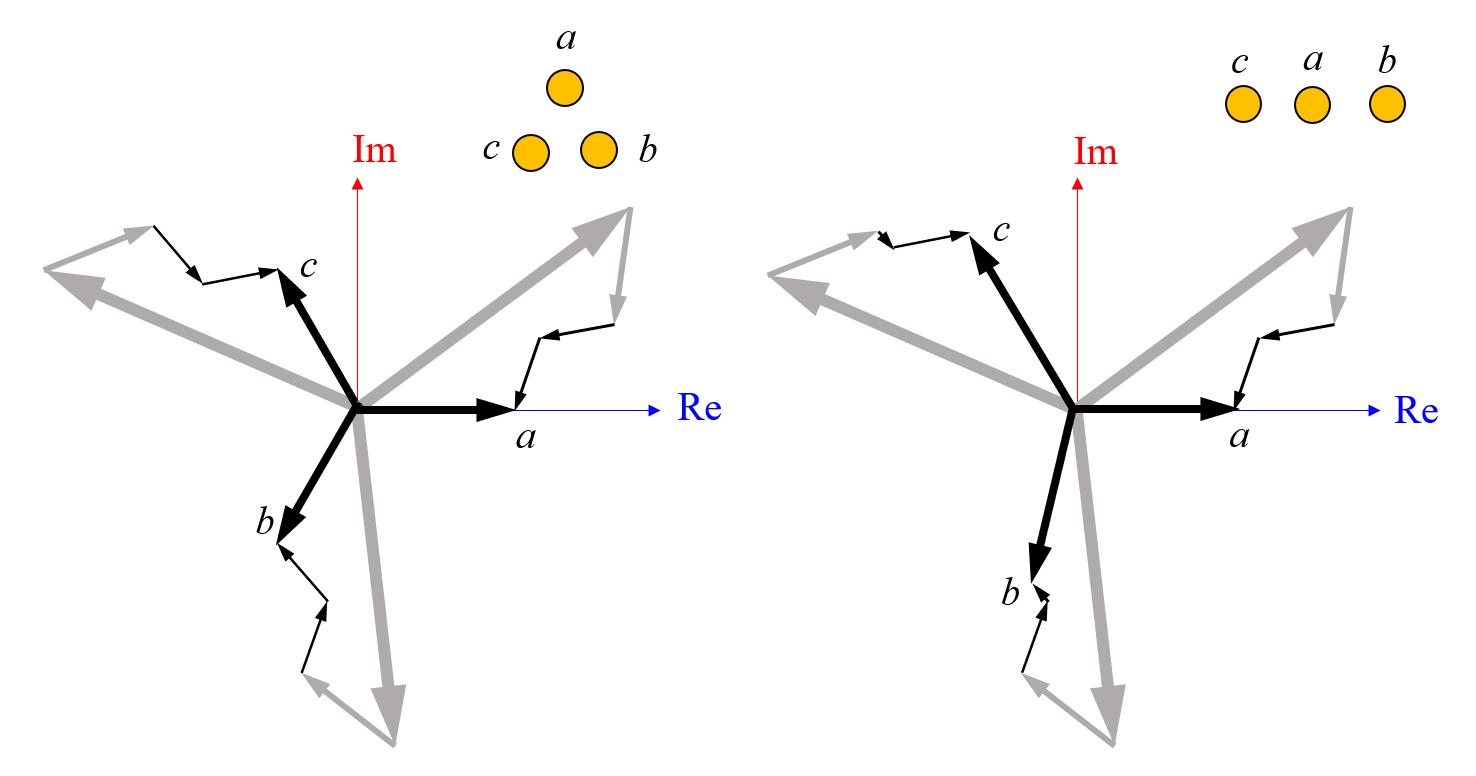
左側では, 三角形配置の電流の合計は対称です. 右側では, 駆動電圧は一定に保たれていますが, 電線が直線状に移動しているため, 誘導電流の大きさが異なり, 対称性が崩れています.

均衡した三相印加電圧は, 均衡しない電流を導かなければならないことが分かります. あるいは, 元のケースに戻り, バランスの取れた電流を得ようとすれば, 印加される電位はすべて異なっていなければなりません. したがって, 損失が同じになることはあり得ません.

終わりに

この系を物理的に検証する場合, 最も簡単に測定できるのは, 各ワイヤーの合計損失です. 外側の 2 本のワイヤーで実験的に測定された合計損失はほぼ同じになり, この小さな差を実験誤差のせいにするのは簡単です. 最初の画像のように, 数値的に計算された損失の分布を確認して初めて, 違いがより明確になります. ただし, 単線内部の損失分布を実験的に検証することは非常に困難であり, そのような実験はこれまでに行われたことがない可能性があります.

これは, この問題についてのさまざまな考え方の 1 つであることにも注意してください. 元のケースでは x 軸と y 軸に関して幾何学的対称性があるにもかかわらず, 対称条件は, 位相が 180° ずれている, つまり 2回対称の磁場のみを許可します.

電線の位相が120°ずれている解は, 正三角形の配置のような3回対称性を必要とします. また, ここで示したものは正式な証明ではないこと, そして視覚的にどれだけ魅力的かがどうであれ, 最も初歩的な結果であっても疑うべきであることを認めることも重要です. さて, 非公式の証明をいくつか提示しましたが, それだけで十分でしょうか?.

もう一つの証拠はモデル自体にあります. 私たちが開始した元のモデルは単純です. 1列に並んだ 3 本の電線が三相電流を流し, 領域, つまり 特異点がない 上の有限要素法を介して求解されます.

場合によっては, 単純なモデルの結果であっても, 直感と一致しないことがあります. そのため, 人々はモデルの間違いを疑うことがよくありますが, すべてのモデルにはある程度の懐疑心と厳格な検証および検証プロセスを持って取り組む必要があるため, これは確かに合理的です.

有限要素法は数理物理学で最も使われ, 検証済みのメソッドのひとつであるにもかかわらず, 有限要素法そのものを疑いたくさえなるでしょう.

最後に, 私たちは自分の直感を信じすぎるという罠に陥ってはなりません. 最も重要な 科学における驚くべき発見は予期せぬ観察から始まるので, 常に広い心を持ってください.