Menu
COMSOL ブログ

基板上の物体からの光の散乱のモデリング

Author Image
Walter Frei 著
2020年 4月 14日

波動電磁気モデリングで頻繁に発生するモデリング状況は, 均一な誘電体基板上にパターン化された構造からの光の散乱を計算することです. このブログでは, COMSOL Multiphysics® ソフトウェアでこのような状況をモデル化する1つの方法を紹介します.

背景と概要

ここで考えるのは, 誘電体基板の上にパターニングされた金の半円筒という, 小さな光の散乱体の場合です. ここでは, 散乱体1つの場合に注目し, 散乱体よりはるかに大きな直径の平行光ビームから照射され, 平面波としてよく近似できると仮定します. この平面波は, 任意の角度, 偏光状態で構造物を照射することができます. 誘電体基板は負のz方向に無限に伸びていると仮定されます.

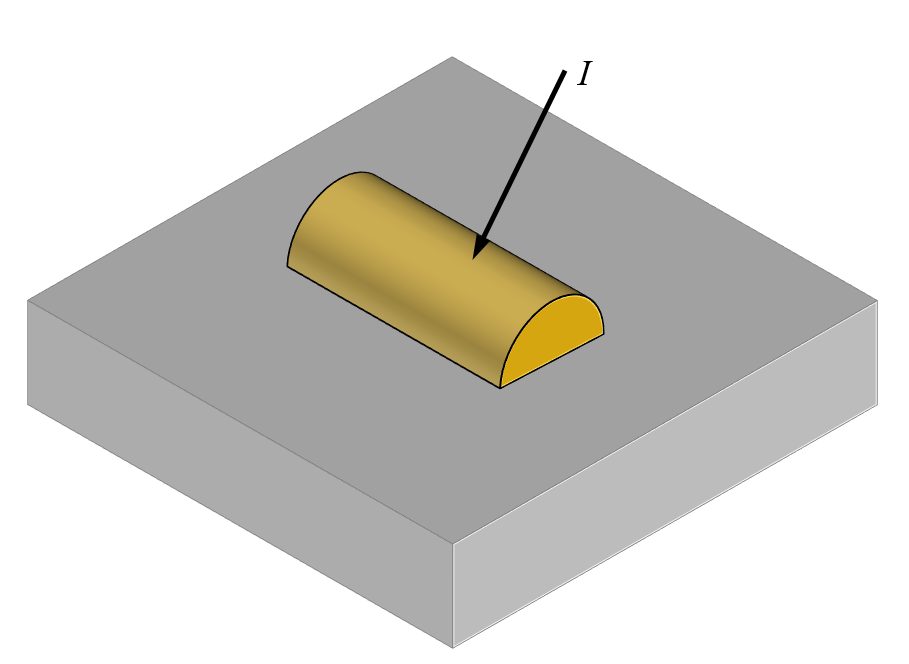
誘電体基板上の単一の散乱体に入射する光の概略図.

半無限誘電体基板上の単一の散乱体に任意の角度で入射する光.

背景場の比較的小さな摂動を表す単一の散乱体のみをモデル化する必要があるため, 散乱場定式化を使用することは理にかなっています. この定式化では, 散乱体がない場合のマックスウェル方程式の解を表す背景電場を入力する必要があります. つまり, マックスウェル方程式を周波数領域の形式で解きます.

\nabla \times \left( \mu_r \nabla \times \mathbf{E}_{total} \right) – \frac{\omega^2}{c_0^2}\left( \epsilon_r – \frac{i \sigma}{\omega\epsilon_0}\right) \mathbf{E}_{total}= 0

しかし, 全電場を次のように記述します:

\mathbf{E}_{total} = \mathbf{E}_{relative} + \mathbf{E}_{background}

全場を解くのではなく, 散乱場とも呼ばれる相対場を解きます. 背景電場は, 散乱体がない場合の問題のドメインに対するマックスウェルの方程式の解です. 自由空間内のオブジェクトの単純なケースでは, RF モジュールのベンチマーク例で使用されているように, 背景場は単純な平面波です. これは,この方法の解を解析結果と比較する, 完全導体球のレーダー断面積の計算です. 波動光学モジュールの同様の例は, 金ナノ球の散乱を計算します. 誘電体の半空間に同じアプローチを使用したくなるかもしれませんが, その場合, 背景場は間違っています.

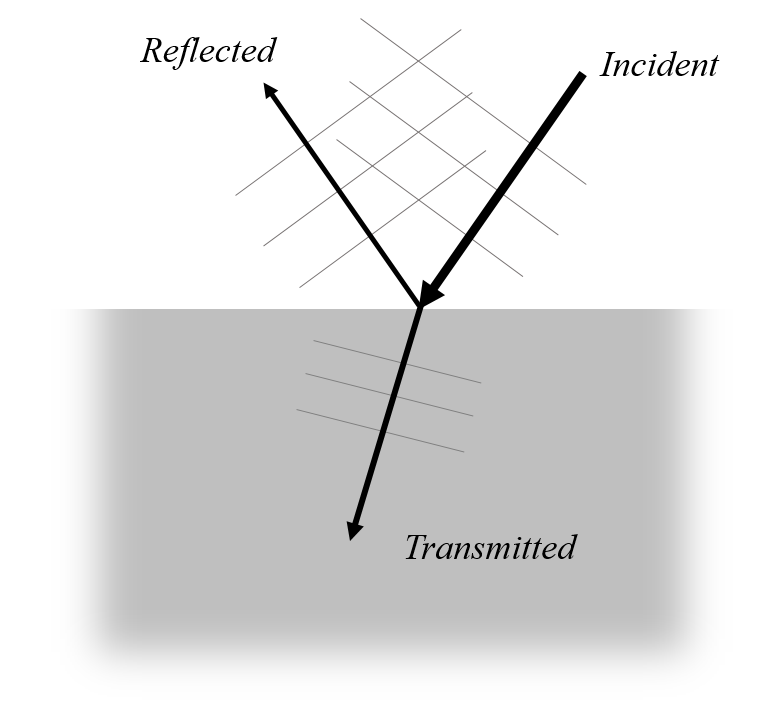
散乱体のない誘電体界面での電場の概略図.

散乱体がない場合の誘電体界面の電場は, 入射, 反射, および透過した平面波の合計です.

半無限無損失誘電体基板上の散乱体の場合, 背景場の式には, 界面での反射と屈折を組み込む必要があります. 1つのアプローチは, 別の解析に基づいて背景場を計算し, その計算された場を背景場として使用することです. このアプローチは, アプリケーションギャラリの基板上の散乱体の例で示されています. ただし, ここでは, 代わりに, 解析解を使用して, 誘電体の半空間に入射する光の背景場に直接入力する方法を見ていきます.

フレネルの式を使用し背景場を定義

フレネルの式は, スネルの法則とともに, 屈折率の異なる2つの材料間の平坦な界面に入射したときの平面波の光の反射と透過を表します. これらのフレネルの式は, 入射面の定義から始まります. これは, 2つの材料間の表面に垂直なベクトルと, 入ってくる平面波の波数ベクトルによって記述される平面です. 入射電場は, s 偏光または TE 波と呼ばれるこの平面に純粋に垂直な成分と, p 偏光または TM 波と呼ばれるこの平面に純粋に平行な成分に分解できます. たとえば, 円偏光は, 同じ大きさのTE 波と TM 波の合計ですが, 互いに90°位相がずれています.

入射面では, スネルの法則を使用して, 2つの材料の屈折率n_a とn_b の観点から, 表面法線に対する入射光 (\theta_t) と透過光 (\theta_t) の角度を関連付けることができます.

\frac{\sin \theta_t}{\sin \theta_i} = \frac{n_a}{n_b}

次に, フレネルの式により, TE 偏光と TM 偏光の反射係数と透過係数が得られます:

\begin{array}

rr_{TE} = \frac{n_a \cos \theta_i – n_b \cos \theta_t}{n_a \cos \theta_i + n_b \cos \theta_t} \\

t_{TE} = \frac{2 n_a \cos \theta_i}{n_a \cos \theta_i + n_b \cos \theta_t} \\

r_{TM} = \frac{n_b \cos \theta_i – n_a \cos \theta_t}{n_b \cos \theta_i + n_a \cos \theta_t} \\

t_{TM} = \frac{ 2 n_a \cos \theta_i }{n_b \cos \theta_i + n_a \cos \theta_t}

\end{array}

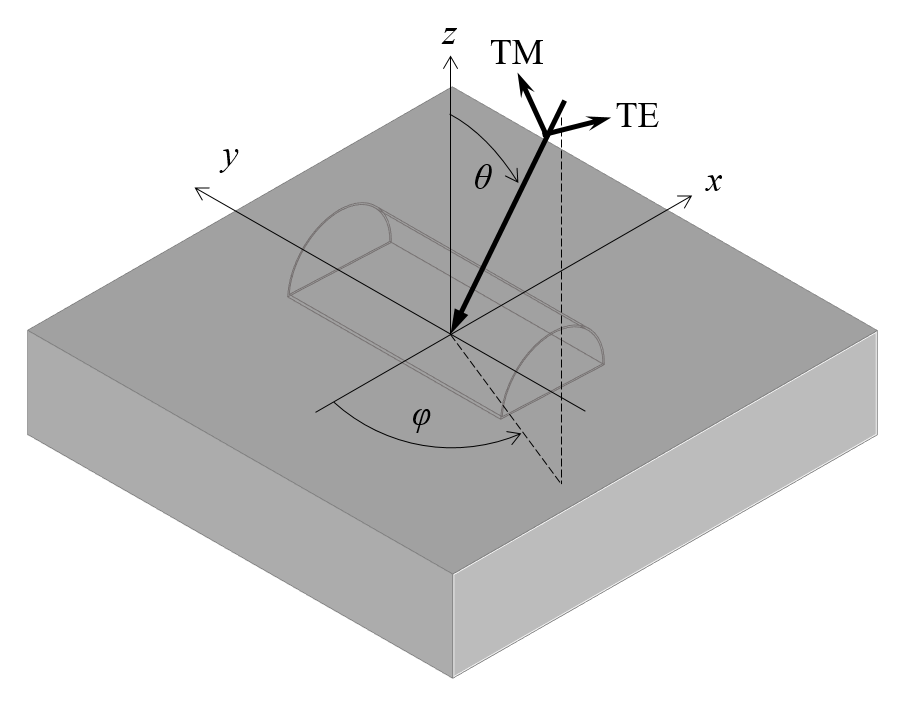
入射平面波の TE および TM 偏光成分を示す概略図

入射平面波の TE および TM 偏光成分は, 入射面からグローバルデカルト座標に変換する必要があります.

次に, これらを入射面からグローバルデカルト座標に変換して, 入射ビームと透過ビームの k ベクトルを取得する必要があります. 界面の平面がxy平面であり, 波長\lambda_0の入射ビームが負のz方向に伝搬しているという慣習に従って, 入射角\thetaをz軸からの角度, および角度\phiと定義します. 上図に示すように, 負のx軸から始まるz軸を中心とした回転として. これにより, 入射ビームの k ベクトルを次のように定義できます.

\mathbf{k}_i = \frac{2 \pi n_a}{\lambda_0} \left \\

そして透過ビーム:

\mathbf{k}_t = \frac{2 \pi n_b}{\lambda_0} \left

反射ビームの k ベクトル は, \mathbf{k}_r入射ビームに似ていますが, z成分の符号が反対です.

TE 偏光成分と TM 偏光成分E_{i,TE} と, E_{i,TM} の両方で構成される入射ビームを考えると, 入射ビームの電場の成分は次のようになります.

E_{i,x} = (E_{i,TM} \cos \theta_i \cos \phi – E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_i \cdot \mathbf{x})
E_{i,y} = (E_{i,TM} \cos \theta \sin \phi + E_{i,TE} \cos \phi )\exp (-i\mathbf{k}_i \cdot \mathbf{x})
E_{i,z} = E_{i,TM} \sin \theta_i \exp (-i\mathbf{k}_i \cdot \mathbf{x})

そして反射成分のために:

E_{r,x} = (-r_{TM} E_{i,TM} \cos \theta_i \cos \phi – r_{TE} E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_r \cdot \mathbf{x})
E_{r,y} = (-r_{TM} E_{i,TM} \cos \theta_i \sin \phi + r_{TE} E_{i,TE} \cos\phi )\exp (-i\mathbf{k}_r \cdot \mathbf{x})
E_{r,z} = r_{TM} E_{i,TM} \sin \theta_i \exp (-i\mathbf{k}_r \cdot \mathbf{x})

したがって, 入射側の全背景場は\mathbf{E}_{background} = \mathbf{E}_i + \mathbf{E}_rであり, 界面の反対側の場は, \mathbf{E}_{background} = \mathbf{E}_tであり, 成分は次のとおりです:

E_{t,x} = (t_{TM} E_{i,TM} \cos \theta_t \cos \phi – t_{TE} E_{i,TE} \sin \phi )\exp (-i\mathbf{k}_t \cdot \mathbf{x})
E_{t,y} = (t_{TM} E_{i,TM} \cos \theta_t \sin \phi + t_{TE} E_{i,TE} \cos \phi )\exp (-i\mathbf{k}_t \cdot \mathbf{x})
E_{t,z} = t_{TM} E_{i,TM} \sin \theta_t \exp (-i\mathbf{k}_t \cdot \mathbf{x})

これらの式は, COMSOL Multiphysics® ソフトウェア内のさまざまなドメインで定義された変数のセットとして入力でき, 背景場定義として使用できます.

光の散乱をモデル化するためのサンプルモデルと考察

このアプローチを示すサンプルモデルが設定され, 以下のリンクから入手できます. 金の小さな半円筒の電場の大きさと損失がプロットされています.

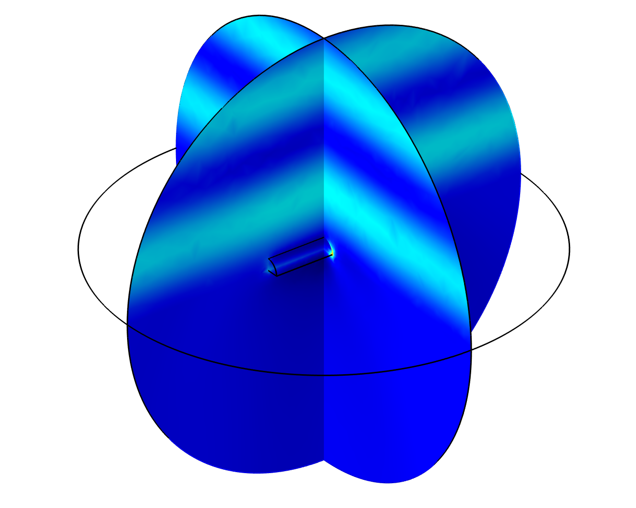
COMSOLMultiphysicsでモデル化された金散乱体の周りの電場の大きさ.

誘電体基板上の金散乱体の周りの電場の大きさ.

金の散乱体での光の散乱を示すシミュレーション

金の散乱体の損失.

解析的背景場を入力するこのアプローチは, モデルの設定に関しては少し手間がかかりますが, 最初に背景場を計算する必要がある基板上の散乱体の例よりも実行が高速です. 後者のアプローチのメリットは, 解析解を書き出すのがより困難であるか, 不可能でさえある場合を検討する場合です. したがって, 均一な誘電体基板の場合, このアプローチが常に望ましいと思われます.

次のステップ

下のボタンをクリックして, 解析的背景場を使用して, 基板上の散乱体をモデリングしてみてください.

MPH ファイルを取得する

コメント (0)

コメントを残す
ログイン | 登録
Loading...
COMSOL ブログを探索
カテゴリー
タグ