以前のブログでは, 線形押出し演算子 を紹介し, ソースと行先の間で変数をマッピングする際の使用法を示しました. 前に説明したように, このアプローチは, ソースと行先がアフィン変換によって関連付けられている場合に限られます. 今日は, 非線形マッピングと, 異なる次元のジオメトリエンティティ間の変数のマッピングを処理するように設計された一般的な押出し演算子について説明します.
押出し演算子の簡単な要約
行先エンティティのポイント P_d で, ソースエンティティで定義された別の量の関数である量を計算します. したがって, ソースポイント P_s からの後者の量を行先エンティティにコピーする必要があります. 押出し演算子は, ソースエンティティのどのポイントが行先エンティティのポイントに対応するかを識別するために使用されます. 言い換えると, 演算子は点対点マップを定義します.
マッピングが アフィン である場合, ソース内のいくつかのポイントが行先エンティティのポイントにどのように対応するかを知るだけで十分です. このようなソースと行先のペアから, 重ね合わせから一般的なマッピングを推測できます. ただし, 一般的には, マッピングの数式を記述する必要があります. これは, ソースポイント P_s を P_d の関数として明示的に定義するか, P_d と P_s の間の陰的な関係のいずれかになります.
COMSOL Multiphysics での一般押出し演算子の使用
線形押出し 演算子を使用する場合, 十分なポイント (ベース) のマッピングを視覚的に示し, COMSOL Multiphysics が残りのポイントの変換方法を判断します. 一般押出し 演算子の場合は, 行先の任意のポイントのマッピングの数学的記述を記述します.
まず, 線形押出し演算子を一般押出し演算子で複製する方法に焦点を当てましょう. 次に, 一般押出し演算子を使用する必要がある例を検討します.
アフィン関係の場合, 一般押出し演算子は線形押出し演算子の代替として使用できます. 一般的な非線形マッピングの場合, 一般押出し演算子が必要です. 一般押出し演算子を追加するには, 定義 > コンポーネントカップリング > 一般押出し に移動します.
例 1
線形押出し演算子に関する以前のブログ では, ソースドメインのポイント 1, 4, 2 を行先ドメインのポイント 1, 5, 3 にペアにするアフィンマッピングについて検討しました. 下の図をご覧ください. ジオメトリ内の2つの円の中心は原点にあり, 半径はそれぞれ 1.0 と 1.5 です.
アフィン変換はいずれも, 線形変換と変換操作の合計として表現できます. したがって, 次の式が成り立ちます
次に, 定数 a,b,c,d,e, および f を見つける必要があります. ソースポイント (0, 0), (1.0, 0), (0, 1.0) は, それぞれ行先ポイント (0, 0), (1.5, 0) に対応します. そして (0, 1.5) の場合, 次のようになります
これで, ソースポイントの対応する座標を見つける方法がわかったので, 行先の任意のポイント (x,y) を指定して, 上記の式の右側 (下付き文字なし) を一般押出し設定ウィンドウの行先マップに入力します.
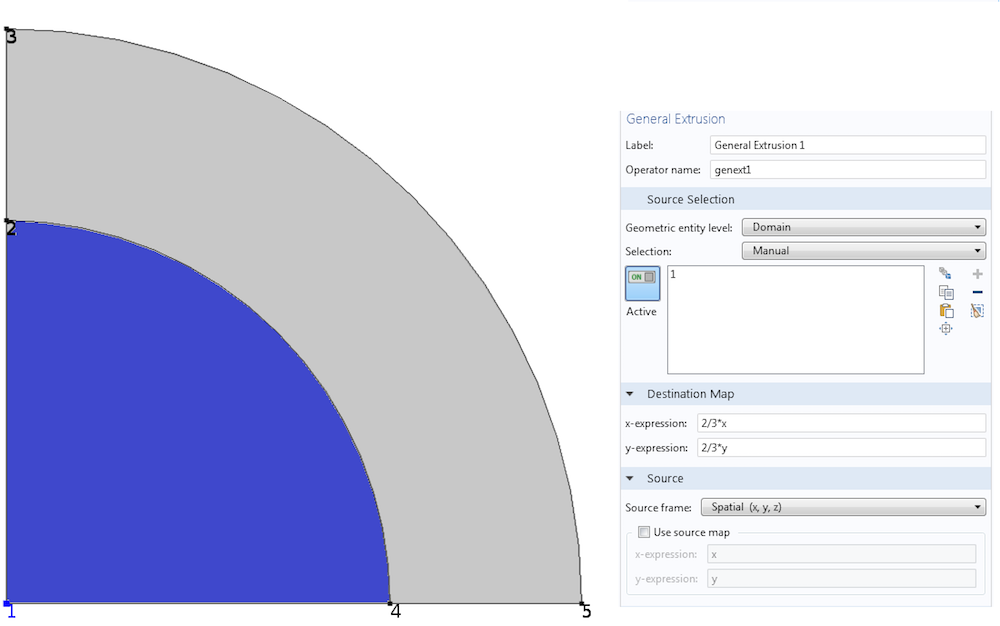
一般押出し演算子を使用して構築された線形マッピング.
例 2
次に, 一般押出し演算子を使用して, ソースポイントとターゲットポイントが空間内の同じポイントに対応するように, 2D軸対称コンポーネントから3Dコンポーネントにデータをコピーする方法を説明します. 軸対称の熱境界条件と材料特性を持つ 熱膨張 について考えてみましょう. 構造境界条件が軸対称でない場合は, 1つのコンポーネントで軸対称熱解析を実行し, 2D軸対称ドメインから別のコンポーネントの構造解析用の3Dドメインに温度をマッピングすることで, 時間を節約できます.
マッピングを構築するときは, 次の質問をすることが重要です. 目的地の座標が与えられた場合, ソースポイントにどのように移動しますか? この場合, その関係は次のように表されます.
例 1 と同様に, 目的地マップの右側に式を入力します.
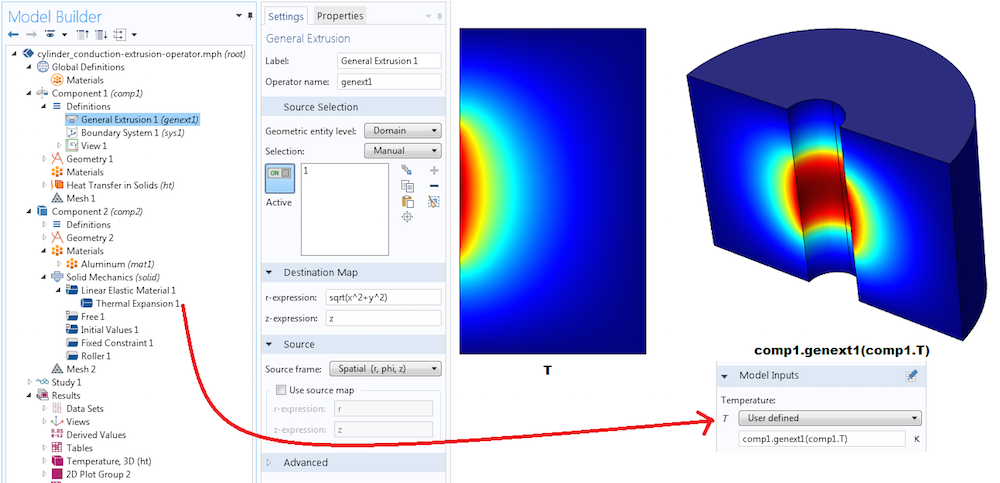
一般押出し演算子を使用して, 2D軸対称ドメインから対応する3Dドメインにデータをコピーします. 軸対称コンポーネントの場合, 変数は結果ノードの回転2Dデータセットを使用して3Dで表示できます. ただし, 2D軸対称コンポーネントの変数を3Dコンポーネントのフィジックスノードで使用する場合 (つまり, 熱膨張), 一般押出し演算子を使用する必要があります.
演算子 genext1 は, 3Dコンポーネント comp2 内では認識されません. T も同様です. 2D軸対称コンポーネントの温度を3Dコンポーネントの入力として使用する場合は, comp1.genext1(comp1.T) を使用する必要があります. このアプローチは, 押出しや, 同じく genext1 と呼ばれる別の演算子, または T と呼ばれる別の変数が2番目のコンポーネントにある場合に混乱を避けるのに役立ちます.
ここでは線形押出し演算子を使用できないことに注意してください. ソースオブジェクトと行先 オブジェクトの次元が異なるため, アフィン変換は不可能です.
これらの最初の2つの例では, 設定ウィンドウのソースセクションにある ソースマップの使用 チェックボックスはオフになっています. COMSOL Multiphysics は, 最初のケースでは x と y を入力し, 2番目のケースでは r と z を入力しました. このチェックボックスがオフになっている場合, COMSOL Multiphysics は, 行先の座標の関数としてソースの各座標に明示的な式があると想定します. ただし, 明示的な式がないこともよくあります.
次に, 一般押出し演算子を使用して暗黙的な関係を指定する方法を見ていきます.
例 3
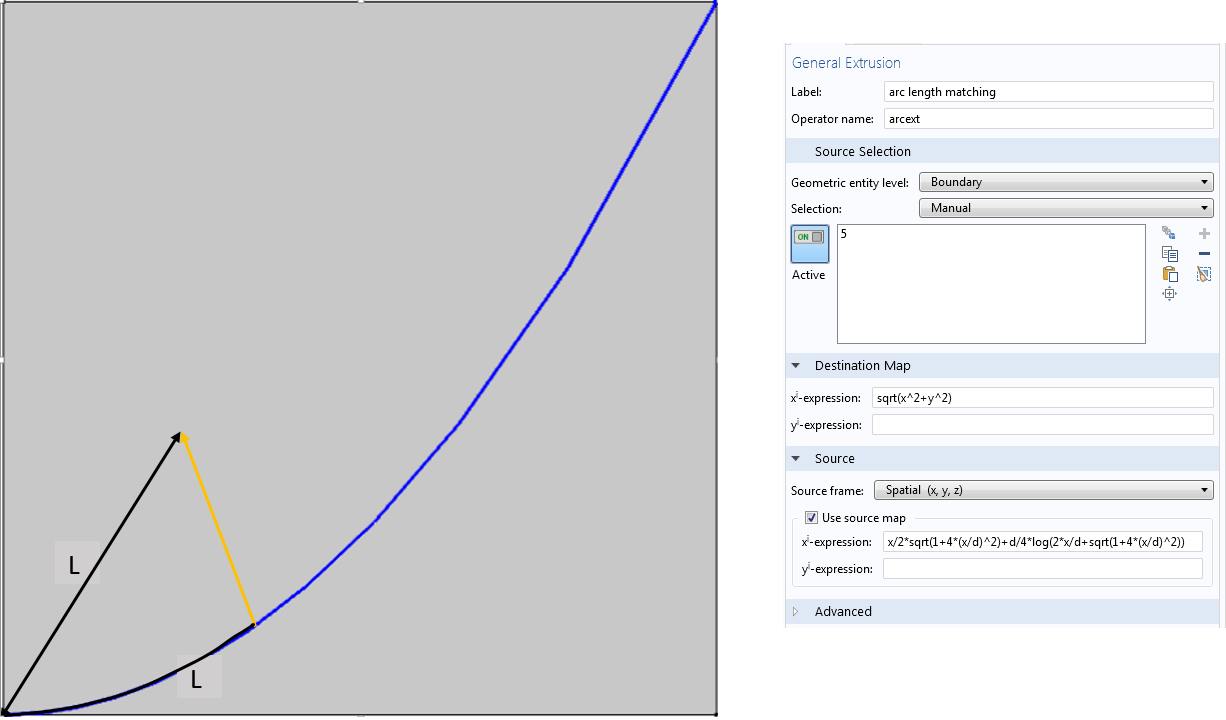
\frac{y}{d} =(\frac{ x}{d})^2 で示される 2D放物線は, エッジ d の正方形領域内にあります. ここでのタスクは, この曲線 (下の図で青で表示) のデータを正方形のさまざまな部分にマッピングする演算子を作成することです. 放物線がソースです. 放物線上の点から正方形内の点にコピーする演算子が必要です. この場合, コピー先の点から原点までの距離は, 原点とソースポイント間の放物線のセグメントの長さに等しくなります.
少し計算すると, 原点とソースポイント (x,y) 間の放物線の弧の長さがわかります.
したがって, ソースポイントとターゲットポイントの関係は次のようになります
という形式の明示的なソース-行先マッピングが必要な場合は, まず式 L=\frac{x_s}{2}\sqrt{1+4(\frac{x_s}{d})^2}+\frac{d}{4}\ln(2\frac{x_s}{d}+\sqrt{1+4(\frac{x_s}{d})^2}) を反転し, x_s を L で記述する必要があります. これはまったく面白くありません.
これがまさに, COMSOL Multiphysics が, 2つのマッピング (行先マップとソースマップ) を使用して, ソース座標と行先座標間の暗黙的な関係を指定できる理由です. T_d と T_s を指定する必要があります.
ソースマップと行先マップを使用して, 一般的な押出し演算子でソース座標と行先座標間の陰的な関係を定義します.
COMSOL Multiphysics は, ソース座標を識別するために必要な手順である T_s^{-1}(T_d(x_d,y_d)) を処理します. 逆が存在するためには, ソースマップが1対1である必要があることに注意してください. 実際には, COMSOL Multiphysics はソースマップの逆の解析式を構築しません. 代わりに, すべての行先 ポイントで, 最初に T_d(x_d,y_d) を評価し, メッシュ検索操作を実行して, この評価が T_s(x_s,y_s) と一致するソース上のポイントを見つけます. 1対1のソースマップでは, 検索によって, 特定のターゲットポイントに対して最大1つのソースポイントが返されます.
上記の一般押出し設定ウィンドウでは, ターゲットマップ と ソース の下のラベルは, x–式 と y–式 ではなく, x^i–式 と y–式 と表示されます. これは, x^i と y^i が, ソースとターゲットの関係を陰的に定義するために使用される最初の式と2番目の式のペアのインデックスであるためです. これらは, 必ずしもソースまたはターゲットの x または y 座標に関連しているわけではありません. これらのインデックスは, ある意味では中間メッシュの座標であり, 一般押出し演算子は同じ中間座標を持つソースポイントとターゲットポイントを一致させます. この例では, 1つの式で, 正方形ドメイン内の任意のターゲットポイントを放物線上のソースポイントに一意に関連付けるのに十分です. したがって, 2行目の y^i–expression は空白のままです.
この一般押出し演算子が変数をどのようにマッピングするかを確認するには, 左端と右端の温度がそれぞれ 300 K と 400 K である平面定常熱伝導問題を考えてみましょう. 上面と下面は断熱されており, 熱源はありません. 温度は x に比例して変化します. 下のグラフから, 右側の arcext(T) のプロットが放射状に変化している理由がわかりますか?
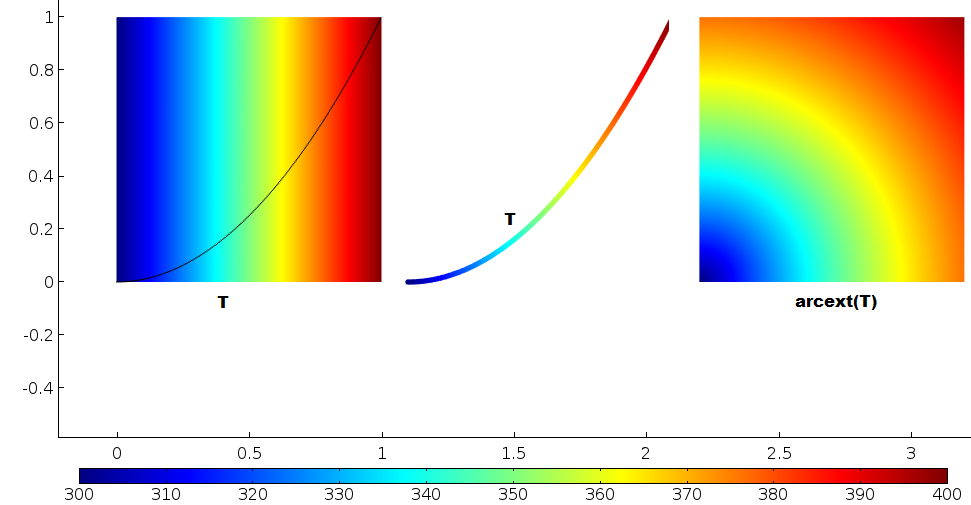
左: 温度は左から右に比例して変化します. 中央: 放物線に沿った温度. 右: 放物線からドメインにマッピングされた温度. 原点から同じ距離にあるドメイン内のすべてのポイントは, 放物線上の同じポイントから温度をコピーします.
すべてをまとめる
これまでに学んだことを応用するために, COMSOL Multiphysics の 電流 フィジックスインターフェースを使用してダイオードモデルを構築しましょう. 押出し演算子を使用すると, 理想的な p-n 接合の両側に通常の電流密度境界条件を構築できます. 下の図に示すように, 異なる側に 1 と 2 のタグを付けることができます. 接合部では, 電流電圧 (I-V) 関係の Shockley ダイオード方程式が使用されます. パラメーター J_s, q, k, \textrm{および } T は, それぞれ飽和電流密度, 電子電荷, ボルツマン定数, 温度を表します.
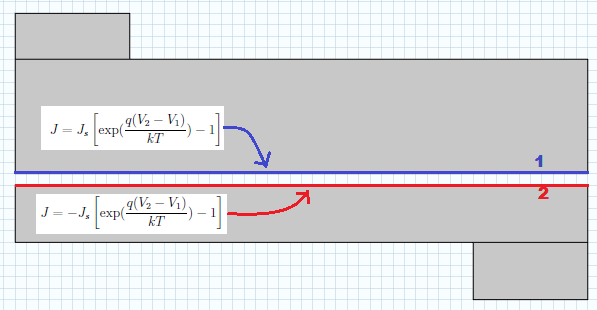
押出し演算子を使用すると, 接合部の反対側の電位にアクセスできます.
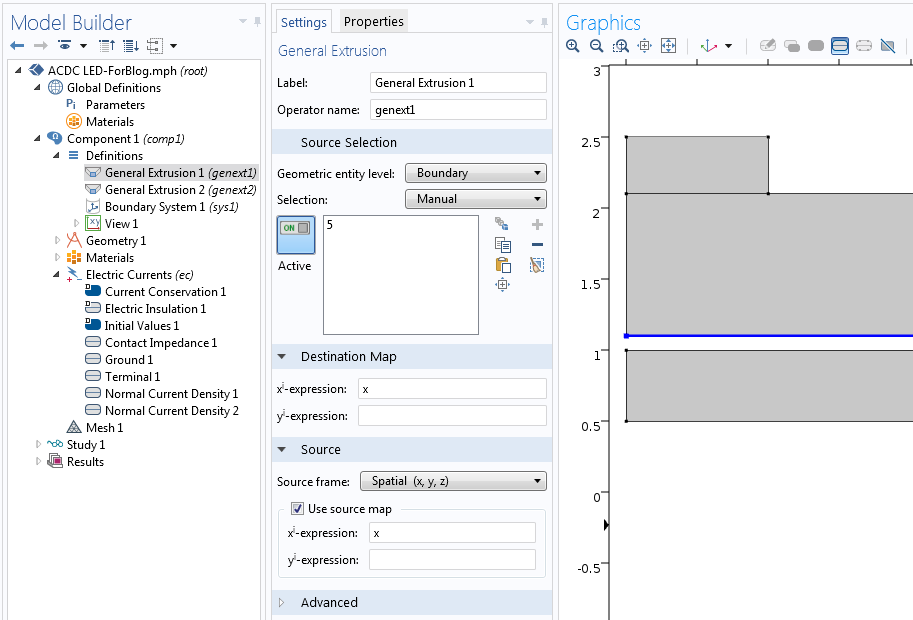
サイド 1 で通常の電流境界条件を実装するには, サイド 2 の電位 V_2 にアクセスする必要があります. 同様に, サイド 2 では, 接合部の反対側の電位 V_1 にアクセスする必要があります. したがって, 2つの押出し演算子が必要です. 以下に示すように, 接合部の各側は, 押出し演算子の1つでソースエンティティになります.
どちらの場合も, 同じ x 座標を共有するポイント間のマッピングが関係します. ソースエンティティが異なるため, 2つの演算子が必要です.
次に, フィジックスノードの演算子を使用して境界条件を実装します. 上側の境界条件を以下に示します. V は上側の点の電位を指し, genext2(V) は下側の垂直方向の電位を指すことに注意してください.
一般押出し演算子を使用して, 接合部の反対側の点の電位を参照します.
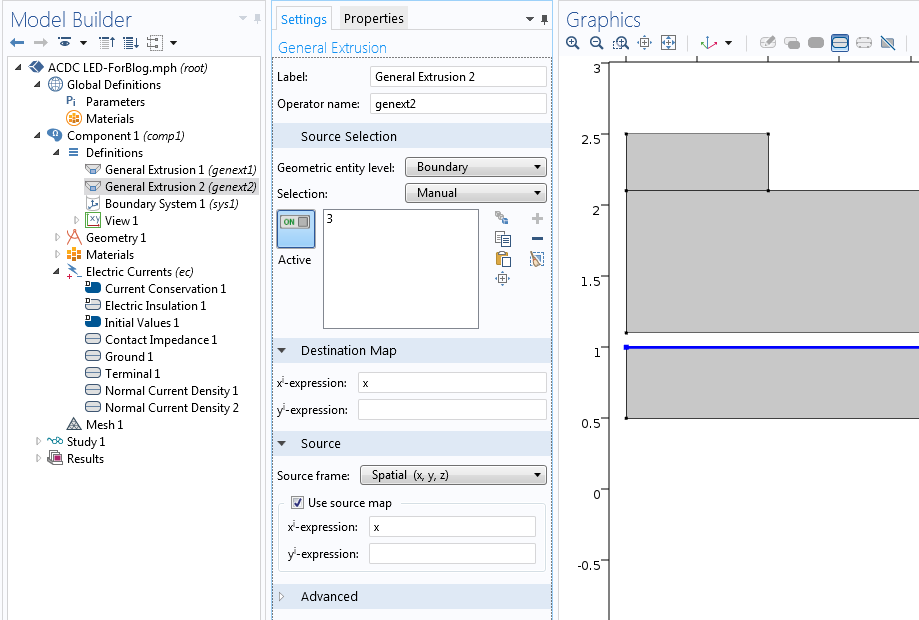
同様の境界条件が接合の下側でも使用されます. エッジ 3 に適用された 法線電流密度 2 ノードの対応する法線電流密度は -Js*(exp((V-genext1(V))/kTbyq)-1) です. ここで, V は下側の点の電位を指し, genext1(V) は上側の垂直方向の電位を指します.
実際, どちらの側に適用されているかに関係なく, 電圧差に式 genext2(V)-genext1(V) を使用することでショートカットを作成できます. わかりやすくするために, ここではこのトリックは使用していません.
デバイスの下部に電圧端子があり, デバイスの上部に接地がある場合, 次の結果が得られます.
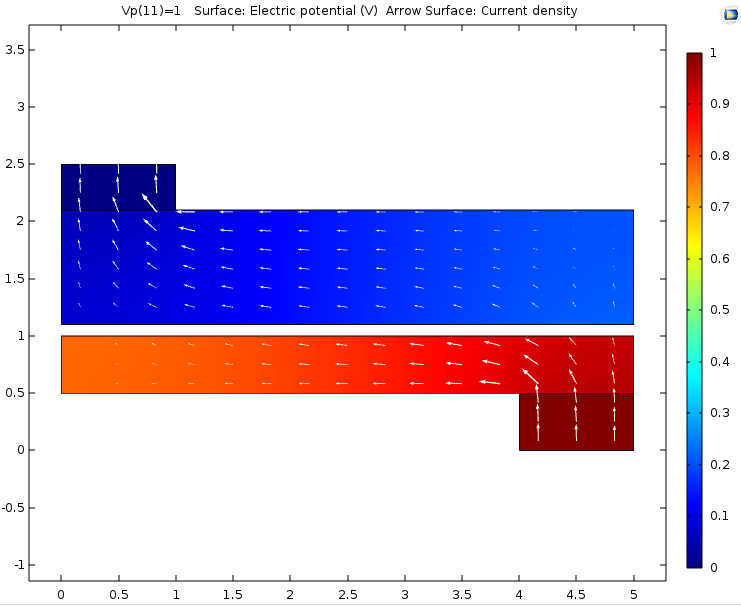
押出し演算子は, 同じコンポーネントまたは異なるコンポーネント内のポイント間のカップリングを作成するために使用できます. ここでは, ダイオードの p-n 接合は, ジオメトリ内の細いギャップで表されます. ギャップの片側の電位は, ギャップを流れる電流密度を計算するために押出し演算子を使用して反対側からアクセスされます.
その他のコンポーネントカップリング演算子
押出し演算子は, ソースポイントと行先ポイント間のポイントごとの関係を構築するために使用されます. 場合によっては, ソースライン, サーフェス, またはボリュームの積分, 平均, 最大値, または最小値にアクセスする必要があることがあります. このような場合, 射影, 積分, 平均, 最大, または最小のコンポーネント結合を使用できます. 投影演算子の使用の詳細については, この 以前のブログ を参照してください.
まとめ
今日は, 一般押出し演算子を使用して, シミュレーション領域のある部分から別の部分に変数をコピーするためのマッピングを作成する方法について説明しました. 既知の量を単にコピーするだけでなく, これらの演算子を使用して, p-n 接合の例で示されているように, 未知の変数間の非局所的なカップリングを作成することもできます. このアプローチは, 構造接触や熱伝達における表面間輻射などの他の解析にも役立ちます. COMSOL Multiphysics には, このような物理的効果に関連する組み込み機能が含まれています.
シミュレーションする非ローカルカップリングが COMSOL Multiphysics の組み込み機能に含まれていない場合は, 今日学んだ戦略を使用して実装できます. ご質問がある場合は, お気軽に お問い合わせください!
その他の資料
他の種類の状況での一般押出し演算子の使用について詳しくは, 次のブログを参照してください:
コメント (0)