
有限要素モデルには, 特異点 (つまり, 解のある側面が無限大値に向かう点) が含まれることがあります. このブログでは, 特異点の一般的な原因, 特異点をいつどのように除去するか, そしてモデルに特異点が存在する場合の結果の解釈方法について考察します. この議論のほとんどは構造力学の観点からですが, 同様の現象は他の多くの物理学の分野でも見られます.
問題
以前, 構造解析コンサルタントとして働いていた頃, 有限要素モデルにおける途方もなく高い応力ピークを顧客に報告する方法という問題に遭遇することがありました. 経験豊富な解析者は, 応力ピークがモデリングの予測可能な影響であり, 安全に無視できる場合を知っています. しかし, “応力は降伏応力の 70% を超えてはならない” という要件が明記されている場合, それでも問題となる可能性があります. 同様に重要なのは, カラープロット内の小さな赤い点を常に無視できるわけではないという事実です. したがって, モデル結果を解釈するための適切な手法が必要です.
鋭角コーナー: 特異点のプロトタイプ
鋭角な凹角は, すべての楕円型偏微分方程式の従属変数の導関数に特異点を引き起こします. 構造力学においては, 自由度が変位であるため, これはひずみが無限大になる可能性があることを意味します. 材料モデルによって制限されない限り, このような場合, 応力も無限大になります.
応力は, ほとんどの構造力学解析で検討されます. これが, 特異点が他のほとんどの物理学分野よりも構造力学においてより大きな問題となる理由です. 例えば, 伝熱解析では, 特異点が顕著になる領域である熱流束の局所値よりも, 温度に関心が寄せられる可能性がはるかに高くなります.
プロトタイプの問題を見てみましょう. この問題では, 2メートル × 1メートルの長方形板 (0.2メートル辺の正方形の切り欠きあり) が純張力を受けるものとします:
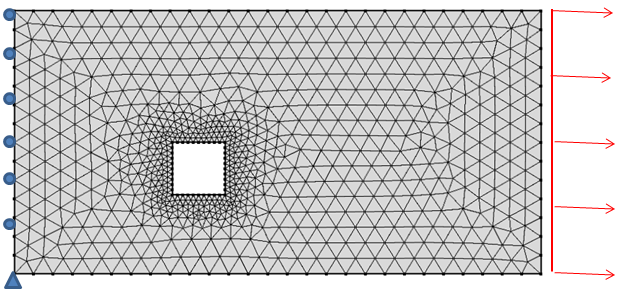
板は左辺に沿って拘束され, 右辺に沿って均一な荷重がかかっています.
穴の周囲に2つの異なるメッシュがあるため, 等価応力のデフォルトのプロットは全く異なるように見えます. 細かいメッシュを持つモデルではピーク応力が2倍になるため, 応力場のほとんどの詳細が失われます. もちろん, プロットの範囲を手動で調整することでこれを修正できますが, 一見すると重要な詳細が見えなくなる可能性があります.
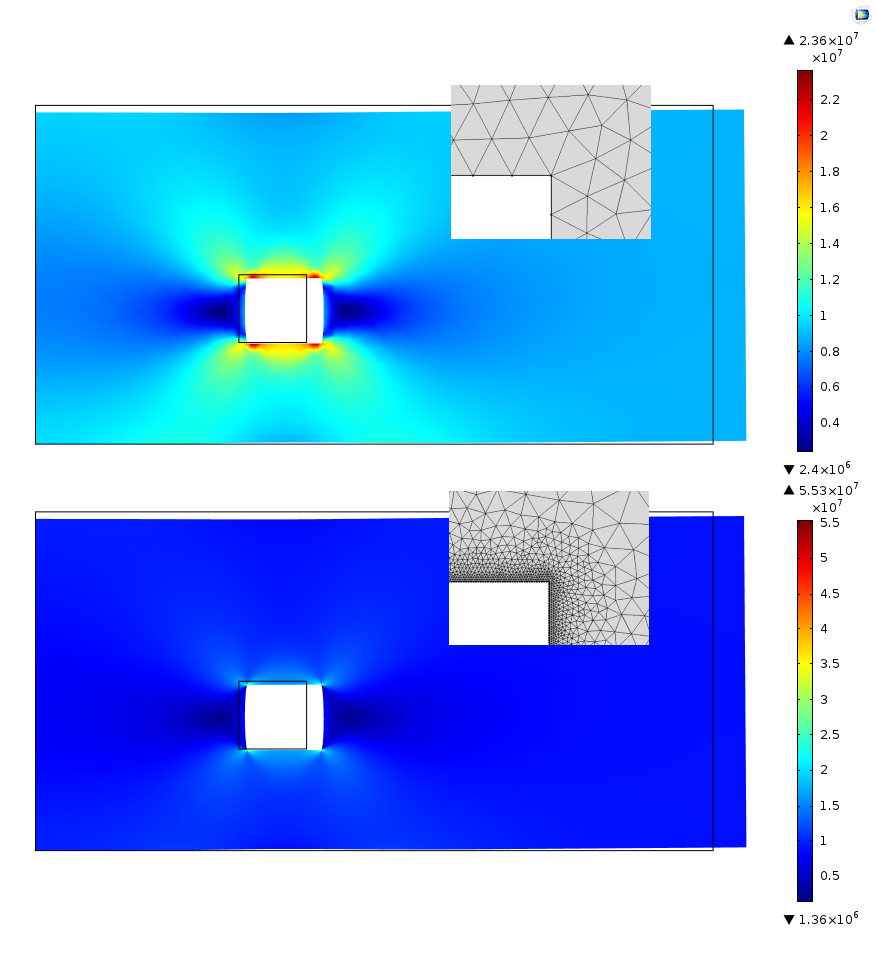
2つのプロットにおける同じ等価応力場. どちらのプロットも, メッシュに依存するピーク応力によって自動的にスケール調整されます.
実際, コーナーで使用される要素が小さいほど, 応力の値は高くなります. 真の解は無限大に近づくため, 結果は収束しません.
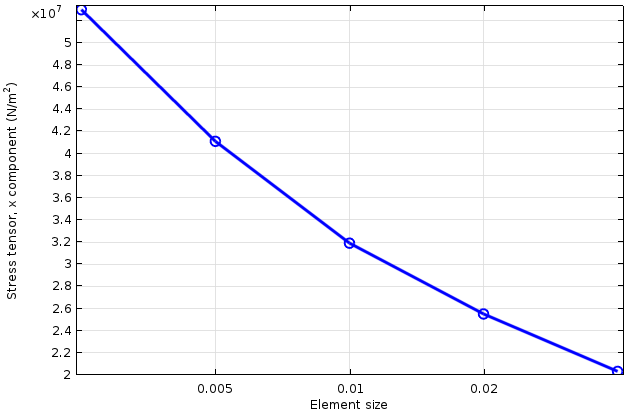
コーナーの応力を要素サイズの関数として表したもの (横軸は対数).
穴の近くの応力場を調べると, 応力のピークが非常に局所的であることがわかります. 下の図は, 穴から0.05メートルの距離に引かれた垂直の切断線に沿って応力をプロットしたものです. この距離では, コーナーのピーク応力が2倍に変化するにもかかわらず, 応力はほとんど変化しません.
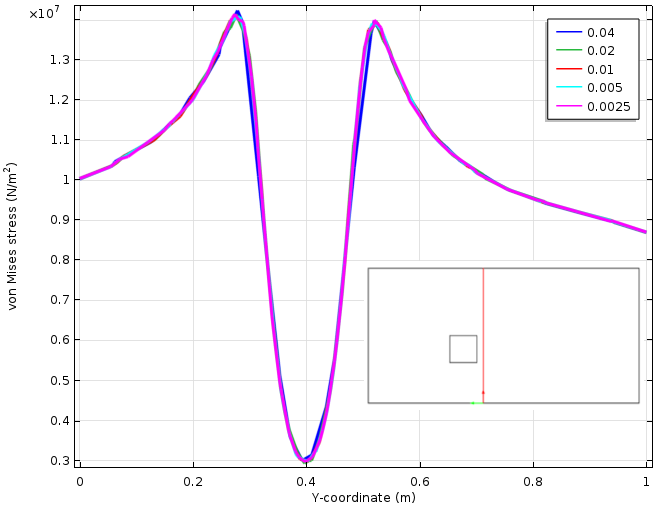
カットラインに沿った応力変化 (赤で表示). 5つの異なるメッシュサイズが使用されています.
現実世界では, 完全に鋭角な角はめったにありません. そのため, すべてのフィレットを含む正確なジオメトリ表現を使用することで, 特異点を回避できると主張することもできます. 確かにその通りですが, これには代償が伴います. 非常に小さな形状の詳細をメッシュで分解する必要がある場合, モデルのサイズは膨大になります (特に3Dの場合). 完璧な CAD ジオメトリが利用可能な場合でも, 解析の範囲では重要でない小さな細部を削除するために, ジオメトリの 細部除去 を行うのが一般的です. そのため, 多くの場合, 前処理の段階で意図的に鋭角コーナーを導入します.
しかし, 鋭角コーナーを維持することにはいくつかの欠点があります:
- 材料モデルが非線形の場合, 特異点において数値的な問題が発生する可能性があります. 例えば, クリープモデルによって予測されるひずみ速度は, 多くの場合, 応力のべき乗に比例します. 特異点における高い応力 (メッシュによってのみ決定される値) を5乗すると, ひずみ速度が非常に高くなり, 実際には数か月かけて発生する事象を解析したいにもかかわらず, 時間ステップがミリ秒単位にならざるを得なくなる可能性があります. それでも鋭角なコーナーを維持したい場合は, 特異点を小さな弾性領域で囲むことが解決策となります.
- 特異点が解の残りの部分を支配するため, アダプティブメッシュ作成や誤差推定などは失敗する可能性があります. コーナーは, これらの手順から除外してください.
- 応力が問題の定式化の一部である最適化を実行する場合, 特異点によって, 非物理的なピーク応力の振幅を低減するという点においてのみ最適な解が導かれます. ブラケットのマルチスタディ最適化チュートリアル では, ブラケットがボルトで固定されている領域は最大応力の探索から除外されています.
- 前述のように, 高い応力ピークは, 視覚的にも心理的にも, 解のより興味深い特徴を覆い隠してしまう傾向があります.
物理的には, 角が非常に鋭い場合, 高いひずみによって材料が損傷します. 脆性材料はひび割れを起こし, 延性材料は降伏する可能性があります. これは恐ろしいように聞こえるかもしれませんが, このような損傷はほとんどの場合, 応力の局所的な再分布を引き起こすだけです. 周囲の構造物から見ると, その影響はフィレット半径を多少変更した場合よりも劇的ではありません. 局所的に高い応力が真の問題となるのは, 荷重が周期的に作用する場合のみであり, その場合 疲労 のリスクが生じます.
建物では, 窓やドアの穴が鋭角な長方形であっても気にする人はいません. しかし, 旅客機では, 客室内の気圧と外気圧の変動によって周期的な応力履歴が生じるため, 窓は滑らかな丸みを帯びています.


左: 鋭角な角を持つ長方形の窓. 画像提供: Jose Mario Pires. Wikimedia Commons を通じて CC BY-SA 4.0 ライセンスの下で使用されています. 右: 角が滑らかに丸められた窓. 画像提供: Orin Zebest. Wikimedia Commons を通じて CC BY-SA 2.0 ライセンスの下で使用されています.
これは多くの設計基準で認められており, 荷重が静的である限り, 高い局所応力が許容されます. 局所的なコーナー応力は, 構造物の耐荷重能力に全く影響を与えません. この種のアプローチは, 応力場を体系的に分類する方法に依存します. そのような方法は, 例えば ASME Boiler & Pressure Vessel Code に記載されています.
一方, 周期荷重の場合, 非常に正確な応力値を取得することが重要です. 疲労寿命は応力振幅に大きく依存します. この場合, フィレットの正確な表現は, 幾何学的だけでなくメッシュ解像度の面でも必要です. モデルが大きくなりすぎて扱いきれなくなった場合は, サブモデリング を使用できます. このアプローチについては, こちらのブログ で詳しく説明しています.

右側の詳細サブモデルは, グローバル解析の結果に基づいています.
ヒント: サブモデリング手法をさらに詳しく知るには, アプリケーションギャラリから シャフトのサブモデリング解析チュートリアル をダウンロードしてください.
点荷重
固体上の一点に力が加わると, 局所的には無限大の応力が生じます. これは弾性理論における古典的な Boussinesq-Cerruti 問題 であり, 応力は荷重が加わった点からの距離に反比例して変化します.
現実世界では, 点荷重は存在しません. 力は常に特定の領域に分散されます. 有限要素解析 の観点から見ると, この小さな領域を解析する労力に見合う価値があるかどうかが問題となります. その答えは, Saint-Venant’s principle にあります. これは, 静的に等価な荷重分布はすべて, 荷重がかかっている領域のサイズと比較して十分に大きい距離では同じ結果を与えるというものです.
したがって, 例えば荷重がかかっている領域のサイズの3倍以内の距離では詳細な結果が重要でない場合は, 結果として得られる力とモーメントが正しければ, 荷重をどのように適用するかは実際には重要ではありません. コーナー特異点の場合と同様に, 特異応力の影響を回避する必要がある場合もあります. 線荷重は点荷重と同様に, 局所的な無限応力を引き起こすことに注意してください.
梁要素またはシェルに垂直な点荷重は特異点を 誘発しない という事実は興味深い点です. 構造要素の曲げは固体力学とは異なる方程式によって支配されます. しかし, シェルの平面に点荷重が作用すると特異点が 誘発されます.
拘束
拘束を反力を加える能力という観点から考えると, 例えば点に適用される拘束に関して, 荷重の場合と同じ結論を導き出せることは明らかです. しかし, それだけではありません. 下図のような, 一見対称的な問題を考えてみましょう. ここでは, 片側に一定の引張荷重が作用する板があり, 反対側には対応するローラー条件が存在します.
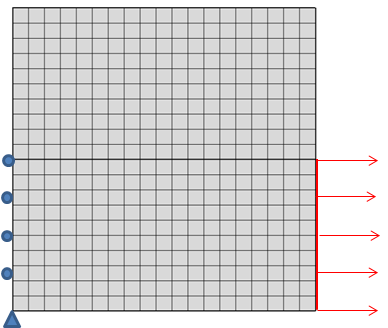
垂直境界の半分が拘束され, 荷重がかかっている正方形板.
応力分布を見ると, ローラー条件の端部が, 荷重の急激な変化では生じない特異点を導入していることがわかります. 一般的に, 拘束の端部は鋭角角と同様の効果をもたらします.
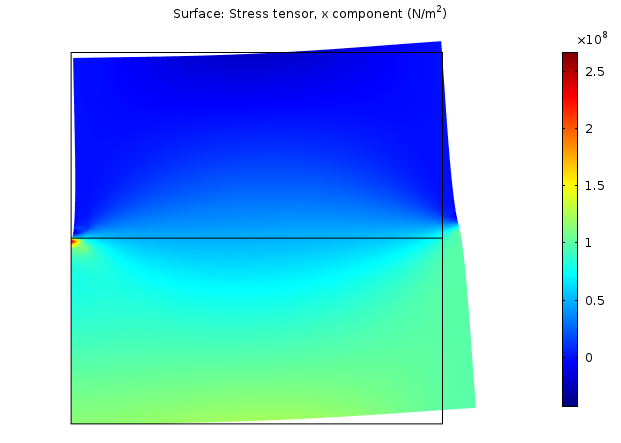
水平応力分布.
構造物を支える無限に剛性の高い環境は, 現実には存在しません. 解析者は再び選択を迫られます. 小さな赤い点をそのまま受け入れるべきでしょうか, それとも構造の外側にあるものにもっと注意を払うべきでしょうか?
境界条件によって生じる特異点が許容できない場合は, 以下のアプローチを検討できます:
- 境界条件によって生じる特異点が関心領域の外側に移動するようにモデルを拡張する.
- 例えば, スプリングファンデーション条件を適用して, より柔軟な境界条件を使用する.
- 計算領域を拡張するための低コストな方法を提供する無限要素を使用する. 詳しくは, こちらのチュートリアル をご覧ください.
上記のような状況は, 多くの種類の遷移において避けられません. このような遷移の例として, 剛性領域と柔軟領域の接続が挙げられます.
溶接
溶接解析の技術は非常に重要かつ複雑なため, 専用のブログで詳しく説明する必要があります. ここでは, このテーマについて簡単に触れるだけにします.
溶接構造物は多くの場合薄板で構成されているため, このような状況ではシェルモデルを使用するのが自然です. 以下のモデルを見てみましょう. この例では, 小さい方の板が広い方の板に溶接されている部分に応力集中が見られます.
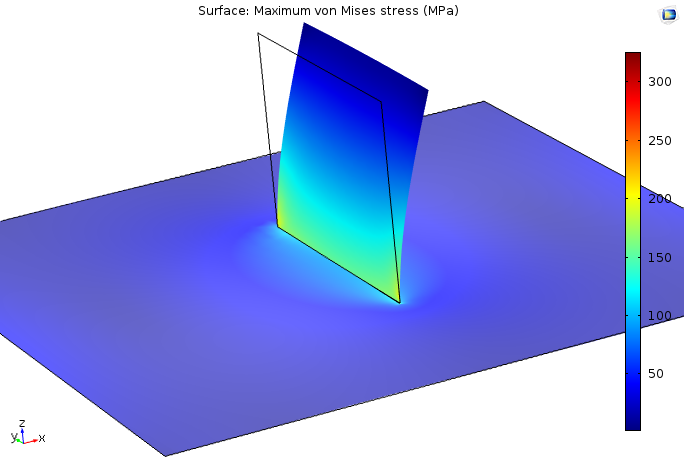
2枚の板を溶接した単純なシェルモデルの応力.
形状と荷重は, 形状の中心に対して対称です. ただし, このモデルのメッシュは, 溶接の一方の端で非常に細かく設計されています. 溶接線に沿った応力のグラフを見ると, 両方の板の応力場に特異点があることがわかります.
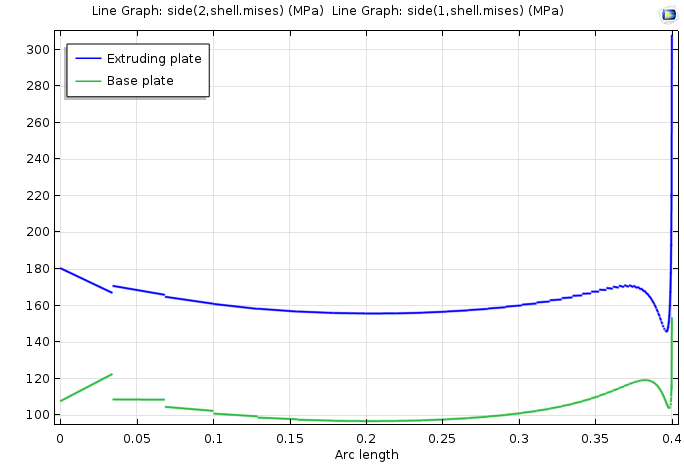
特異点を示す応力分布.
船体, 貨物クレーン, トラックのフレームなど, 多くの溶接構造物では, 疲労を考慮した寸法設定が重要です. ソリッドモデルを用いてモデリングプロセスを精緻化しても, この問題を解決できるケースはほとんどありません. 溶接部の局所的な形状や品質は, 研磨やX線検査が行われない限り, 明確に定義されることはほとんどありません. 溶接部の形状は, 溶接部に沿って, また名目上は同一であるはずの2つの部品においても, 対応する溶接部間で異なります.
溶接を解析する際, 最も一般的なアプローチは, 溶接線または一定距離離れた平行線に沿って応力を平均化することです. COMSOL Multiphysics のカットラインは, 特にこの点で役立ちます. 溶接線に平行な応力成分と垂直な応力成分は異なる扱いをする必要があるため, 局所座標系も役立ちます. これらの平均応力は, 様々な溶接構成と溶接品質に対応したハンドブックの値と比較されます. 詳細については, Eurocode 3: Design of steel structures — Part 1-9: Fatigue を参照してください.
ひび割れ
考えられる最悪の幾何学的特異点は, ひび割れによって引き起こされるものです. 亀裂は 180° の凹角を持つ角と見なすことができるため, 角の特異性に関する多くの側面がここでも適用可能です. 有限要素モデルに亀裂が存在する場合, 通常はそれが研究の焦点となります.

亀裂先端周辺の応力場 (変形をスケール表示).
亀裂先端周辺の応力場は, 少なくとも線形弾性および塑性解析においては, いくつかの仮定の下で解析解から得られます. しかし, 特異性のために有限要素解析による応力場の計算が困難になる場合があります. 幸いなことに, 通常は亀裂先端の詳細を研究する必要はありません. 例えば, 応力拡大係数を決定する際には, J-integral または energy release rate アプローチのいずれかを使用できます. これらの手法は, 亀裂先端から遠く離れたグローバルな量を利用するため, 特異点における詳細はそれほど重要ではありません.
ヒント: J 積分アプローチの使用方法をさらに詳しく知りたい場合は, アプリケーションギャラリの シングルエッジクラックチュートリアル をご覧ください.
結論
多くの有限要素モデルでは, 様々な理由から特異点が発生します. 結果の解釈方法と, その結果の一部を回避する方法さえ理解していれば, 特異点の存在はモデリングにおいて問題にならないはずです. 実際, 多くの産業用モデルでは, 意図的に特異点を利用する必要があります. モデルのサイズと解析時間を抑えるために, 幾何学的詳細, 荷重, 境界条件を簡略化し, 特異点を導入する必要が生じることがよくあります.



コメント (0)