光学設計を解析する際には, 光の強さだけでなく, 偏光も考慮することが重要です. 光の偏光を注意深く操作することで, 不要な光源からの光を遮断し, 例えばグレアを最小限に抑えるなど, 画質を大きく向上させることができます. 光の偏光とその操作方法について学ぶには, フレネルロムを利用するのが便利です. COMSOL Multiphysics® ソフトウェアを使用すると, 光学系における光の偏光に対するフレネルロムおよび類似の要素の効果をモデル化することができます.
直線偏光と円偏光の操作
1800年代初頭, 光学分野の研究と発明で知られる Augustin-Jean Fresnel は, 光を直線偏光, 円偏光, 楕円偏光と表現した最初の科学者でした. 直線偏光の平面電磁波では, 電場の2つの横成分が互いに位相が合っています. これらの成分は, 同じ位置で最大になり, また同じ位置でゼロになる正弦または余弦関数と考えることができます. 次の図は, 直線偏波のプロットです. 波の電場そのものは黄色で表示され, x成分とy成分はそれぞれ赤と緑で表示されています.

直線偏光の平面電磁波.
この直線偏光と下図の円偏光を比べてみてください. ここでは, 電場のx成分とy成分の大きさは同じですが, 90°の位相遅れでオフセットされています. そのため, 一方の成分が最大値または最小値になると, もう一方の成分はゼロになります. このため, 2成分の和が螺旋状になり, 円偏光と呼ばれます.
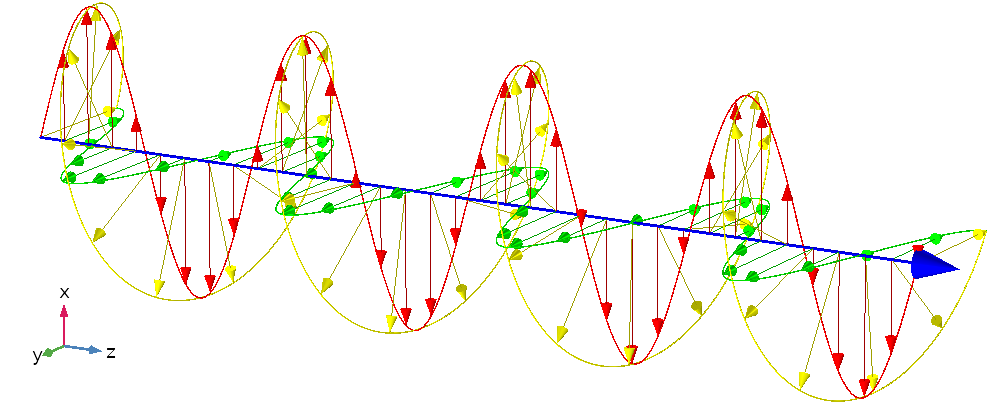
円偏波平面電磁波. x成分とy成分はそれぞれ赤と緑で示されています. 伝搬方向は青色, 全電場振幅は黄色で表示されます.
直線および円偏光放射のフレネルの発見は, 光が純粋な横波 (縦波を含まない) であるという彼の仮説を支持しました. つまり, 電場と磁場の振動は常に伝播方向に垂直です. 光の偏光をさらに解析することにより, 彼は, 光の全反射 (TIR) が, 以前考えられていたように, 入射する直線偏光を偏光解消するのではなく, 楕円偏光または円偏光に変えることを説明できました. TIR による円偏光の生成は, 光が2つの反対側の面で TIRを受ける平行六面体によって便利に実証できます. これは, 現在フレネルロムとして知られている設定です.
フレネルロムは, 光の偏光を操作するガラスプリズムの一種です. 入射光は, 入射面に対して45°の角度で直線偏光されます. 次に, 光は2つの異なる面で TIR を受けます. TIR の各インスタンスは, 入射面で偏光され, 入射面に垂直な電場成分間で45°の位相遅延を引き起こし, 合計で90°の位相遅延を引き起こします. したがって, 出力光は円偏光されます.
COMSOL Multiphysics® とアドオンの光線光学モジュールを使用することにより, 光が光学系を伝搬する際の偏光を予測できます. これは, 光線光学モジュールが, ストークス・ミュラー計算法, または単にミュラー計算法を使用して光の強度と偏光を記録するためです. これは, あらゆる偏光状態を完全に表すことができます. 次のセクションでは, フレネルロムの特定の入射角で直線偏光から円偏光に変化する光を示すチュートリアルモデルを見てみましょう.
COMSOL Multiphysics® を使用したフレネルロムのモデリング
フレネルロムの形状は, 平行六面体の形をした単純なコーティングされていないガラスプリズムです. ジオメトリの簡単な図を以下に示します.
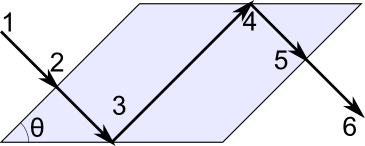
直線偏光 (1) がプリズム (2) に入ります. この光は, 入射面に対して45°直線偏光されます. つまり, スクリーン内にあり, スクリーンに垂直な電界の成分は同じ大きさであり, 同相です. プリズムの角度 (θ) は, 適切に設定されている場合, TIR (3および4) の各インスタンス中に直交電界成分間に45°の位相遅延を引き起こします. 次に, 光はプリズム (5) を出ます. 発信光 (6) は円偏光になります. 画面にあり, 画面に垂直な電界の成分は, 同じ大きさですが, 位相が90°ずれています.
コーティングされていない表面での TIR によって引き起こされる位相遅延の正確な値は, 表面の両側の屈折率n1とn2, および入射角θに依存します. これらの量と位相遅延の関係は, スネルの法則とフレネルの式から導き出すことができます. (方程式の詳細については, フレネルロムモデルのドキュメントを確認してください.)
2 \times \textrm{atan}\left(\frac{\cos\theta\sqrt{\sin^2\theta – \left(n_2/n_1\right)^2}}{\sin\theta}\right) = 45^{\circ}
モデルは2つのスタディで構成されています. 最初に, 45°の望ましい位相遅延を与えるθの値が解かれます. 次に, この角度を使用して, 光線光学シミュレーションのジオメトリを定義します.
スタディ1: 入射角を解く
まず, グローバル ODE および DAE インターフェースを使用して, 屈折率比n= 1 /1.51 の各 TIR 中にs偏光成分とp偏光成分の間でδ= 45°の位相遅延を引き起こす入射角について上記の方程式を解くことができます. (この方程式は常微分方程式や微分代数方程式ではありませんが, このインターフェースを使用して解くことができます.) この例のθの結果の値は 0.84855 ラジアンまたは 〜48.618°です.
スタディ2: 光線の経路をたどる
次に, 幾何光学 インターフェースを使用して, グローバル ODE およびDAE インターフェースによって計算された入射角で TIR を受けるときに, フレネルロムを通る光線の経路を追跡できます. この段階では, 光線は直線偏光されており, 偏光方向は入射面に対して45°の角度になっていることに注意してください.
スタディ1で得られた入射角の値 (0.84855 ラジアン) を使用して, 3D ジオメトリに押し出された平行四辺形であるフレネルロムのモデルジオメトリを設定できます. 3D 光線軌道プロットは偏光楕円を表示できるため, 光線偏光の状態を説明するのに役立つため, 3D ジオメトリを使用することをお勧めします. このステップでは, 各光線の軌道に沿って計算されるストークスパラメーターを使用して, 光線が直線偏光または円偏光される程度を記述します.
シミュレーション結果の評価
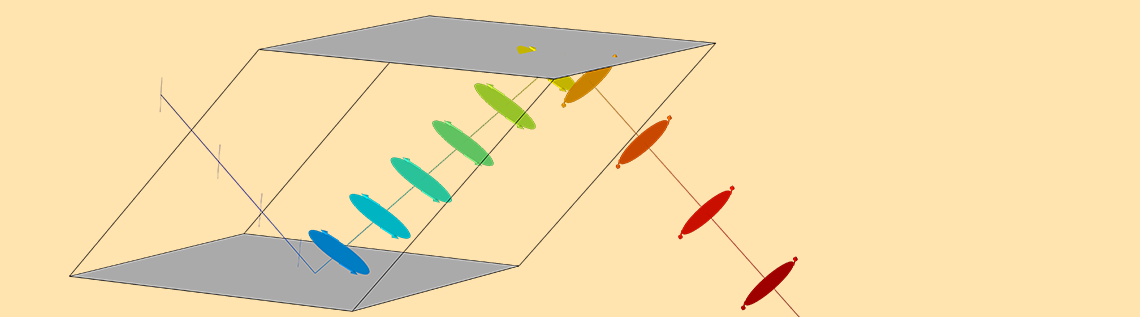
それでは, 前述の光線軌道プロットのシミュレーション結果を詳しく見てみましょう. 以下に示すこのプロットでは, 線形光線はプリズムの左側から入ります. 色は光線に沿った光路長を示し, 光線経路に沿った円と楕円は偏光を示します. 各円/楕円の周囲に沿った矢印は, 瞬間的な場のベクトルの回転の感覚を示しています.
光がフレネルロムを通過すると, 直線偏光された光線は1 TIR 後に楕円偏光になります. 2回の TIR の後, 偏光楕円は円に変わります. これは, 光が円偏光されることを意味します.
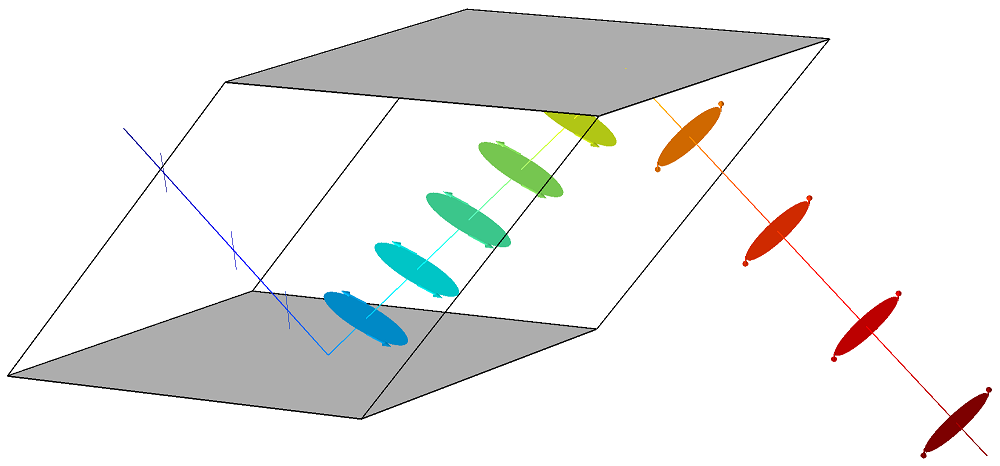
フレネルロムでの光線伝搬.
このカメラアングルでは, 光が円形であることが明らかでない場合があります. しかし, グラフィックスウィンドウで3D プロットを回転させると, 光が直線偏光から楕円偏光, 円偏光に変化することがわかります.
直線偏光 (δ = 0), 1回の反射後の楕円偏光 (δ = 45°), 2回の反射後の円偏光 (δ = 90°) の場合のフレネルロムの入射光を示すアニメーション.
ストークスパラメーターの比率をプロットすることにより, この偏光を別の方法で可視化できます. その結果を以下に示します. まず, 光線は直線偏光され, 比率はゼロになります. 最初の TIR の後, 比率は0から1の間の大きさの値を持ち, 楕円偏光の程度が変化することを示します. 次に, 2回目の TIR の後, 大きさはほぼ正確に1になり, 円偏光とより整列します.
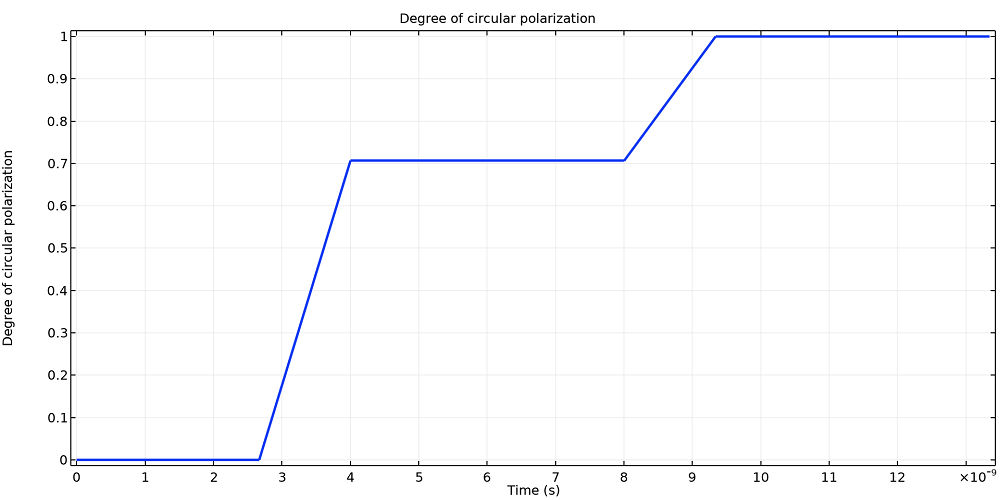
光路長の関数としてプロットされた4番目と1番目のストークスパラメーターの比率.
次のステップ
このブログで紹介されているフレネルロムモデルを試すには, 下のボタンをクリックしてください. 次に, アプリケーションギャラリで, この例のステップバイステップのドキュメントと付属の MPH ファイルをダウンロードできます.
フレネルロムチュートリアルの自然な拡張は, プリズム表面に薄い誘電体コーティングを適用することです. 誘電体コーティングは, 界面のフレネル係数に影響を与えます. したがって, 面内電界成分と面外電界成分の間の位相遅延に影響を与える可能性があります. この例として, TIR 薄膜アクロマティック移相器 (TIRTF-APS) があります. 薄膜を使用してガラスの屈折率の周波数依存性を相殺し, 出力光が広範囲の波長で円偏光を維持するようにします.
参考文献
光線光学モデリングについてもっと知りたいですか? これらのブログを見てください:



コメント (0)