COMSOL Multiphysics^® での差動インダクタンスとコイルの使用

コイル, 非線形材料, 磁石, 可動部品を含む低周波電磁システムをモデル化する場合, 差動インダクタンスの計算が重要になることがよくあります. 差動インダクタンスは, 時間とともに変化する電流がコイルの 1 つに流れるときに, このような電磁システムで発生する場を定量化します. 差動インダクタンスは, 簡素化された集中モデルを構築する場合に特に役立ちます. COMSOL Multiphysics^® ソフトウェアのアドオン製品である AC/DC モジュール内でこれらの差動インダクタンスを使用する理論と実践について, 背景をいくつか説明します.

理論の簡単なレビュー

インダクタンスの概念は, 電流が流れる 1 つ以上のワイヤーループがある場合に関係します. これらのループ, つまりコイルは, 1 巻きまたは複数巻きのワイヤーで構成されます. コイルの 1 つに接続された電源を考え, これを1次と呼びます. また, 他のコイルに接続された負荷を考え, 2次と呼びます. これらの負荷は, 他の電気機器の任意の組み合わせを表すことができます.

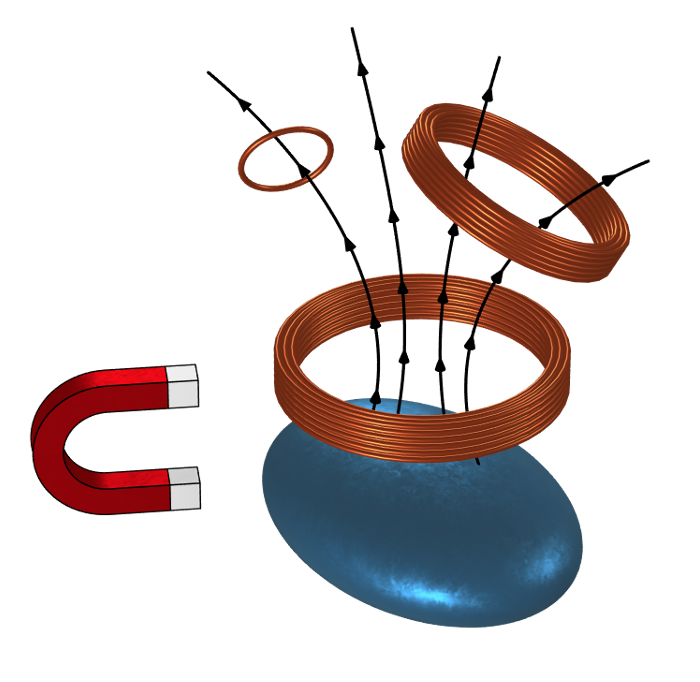
宇宙空間に複数のコイルがあり, その近くには非線形磁性材料と磁石があります. 1 つのコイル内の時間変化する電流は, 遮断された磁束に比例して他のコイルに磁場を誘導します. これは, 非線形磁性材料のバイアス方法によって異なります.
コイルの周囲の空間には, 非線形磁性材料と磁石が存在する場合があります. 非線形磁性材料は, 磁石, コイルの 1 つを流れる電流, またはその両方によって非線形状態に駆動されます. 時間とともに変化する電流が一次コイルに適用されるときはいつでも, 1次コイル自体を含むすべてのコイルに誘導起電力 (電圧) が発生します. 適用される信号の周波数がシステムの共振周波数よりはるかに低いと仮定すると, この起電力は時間とともに変化する磁場によるものであると仮定すれば十分です. この仮定の下では, コイル 機能が関連します.

インデックス i のコイルの 1 つに流れる時間変動電流を考えると, インデックス j のコイルの起電力は, 磁束鎖交の変化率に比例します¹:

\Phiが瞬間電流の関数であるという仮定の下でチェーンルールを適用すると以下のようになります. :

誘導電圧は, 電流に対する微分インダクタンス L’_{ij} と, 印加電流の変化率 \dot{I_i} の積であることがわかります. システム内のすべての材料が線形で, 磁石が存在せず, 導体の誘導損失を無視すると, 次のように簡略化できます:

ここで L_{ij} はセカントインダクタンスであり, コイル 機能が使用されるたびにデフォルトで計算されます. 一方, 微分インダクタンスを計算するには, いくつかの追加手順が必要です.

差動インダクタンスの計算方法を理解するには, まず磁束鎖交に注目する必要があります. これは, 入門用の工学教科書で一般的に, コイル i の励起による磁束が表面 S_j を通過し, コイル j を表す細いワイヤーループで囲まれた \mathbf{B}_i の積分として説明されています:

しかし, 上の画像からわかるように, ほとんどのコイルは大きな断面積を持っているため, 単純に表面 S_j を定義することはできません. 代わりに, 発散定理と \mathbf{B=\nabla \times A } という事実を適用し, コイルに電流が流れる方向 \mathbf{ J } を点線で囲んだ磁気ベクトルポテンシャル \mathbf{ A } の体積積分として \Phi を計算します:

この量は, コイル機能を使用するたびにソフトウェアによって自動的に計算され, コイル連結磁束と呼ばれます.

この連結された磁束は, さまざまな変数の関数になることがあります. ただし, これまでは瞬間電流のみの関数であると想定していました. 次に, 微分インダクタンスを抽出するために導関数を計算する方法を見てみましょう.

差動インダクタンスの計算

微分インダクタンスを計算するには, すべてのコイルのコイル連結磁束の微分を, 1 次側に印加された電流に対して評価する必要があります. これは, 以前にブログ COMSOL Multiphysics^® で設計感度を計算するで取り上げた 感度 インターフェースを使用して実行できます. ここで簡単に説明します. このインターフェースの使用方法は, コイル連結磁束の式を入力する グローバル目的関数 機能の定義から始まります. また, 少なくとも 1 つの 目的制御変数 を定義する必要があります. これは, 目的関数の微分を取るために使用される変数です. ここでは, 1次側に流れる DC 電流を乗算する変数名を入力します. この設定により, 感度スタディステップを印加電流の補助スイープと組み合わせることができ, 印加電流の範囲にわたる差動インダクタンスを計算できます.

 
感度インターフェース内で目的関数を定義します.

 
感度インターフェース内で制御変数を定義します.

 
コイル機能内の制御変数を使用して, 電流に関する微分を設定します.

 
感度の計算と組み合わせて, 電流の範囲をスキャンします.

 
求解後, 評価グループを参照する補間関数を作成し, 差動インダクタンス計算の結果をモデル内の他の場所で使用できるようにします.

理論とワークフローの基礎を念頭に置いて, いくつかの例を見てみましょう.

非線形インダクター

まず, 損失が非常に少ない非線形磁性材料である合金粉末コアフェライトで作られた磁気コアをモデル化します. コアはコイルを包み込み, 内側と外側を囲みます. モデルは 2D 軸対称として扱います. コイルは 1 mm 径のワイヤーを 80 回巻いたもので, 50 Hz で動作しているため, これらのワイヤーの表皮効果は無視できます. したがって, コイルの AC 抵抗は DC 抵抗によって非常に正確に予測されます. この状況では, マルチターンコイルドメイン機能を使用できます. このモデルを時間領域で解き, 正弦波の印加電圧に応じてインダクターを流れる非正弦波電流を取得できます.

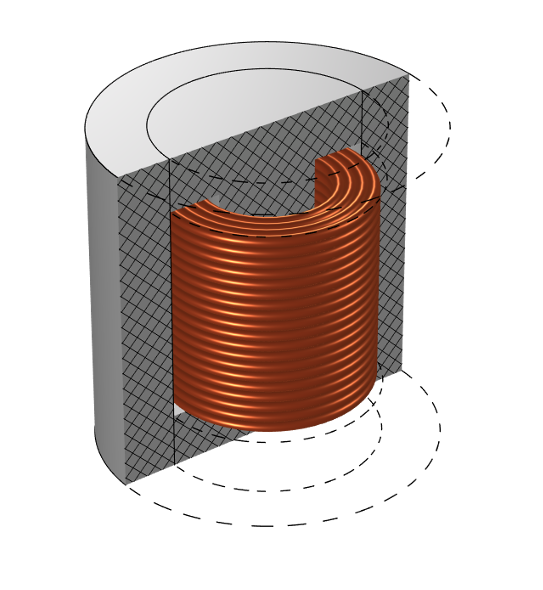
BH非線形コアの周りのコイルで構成されたインダクターの3Dモデル.

まず, このモデルを DC 電流の範囲にわたって解き, 以下にプロットされているように, 比較のためのセカントインダクタンスとともに差動インダクタンスを取得します.

 
非線形磁気コア材料を使用したインダクターの, 印加された DC 電流の範囲にわたる微分インダクタンスとセカントインダクタンス.

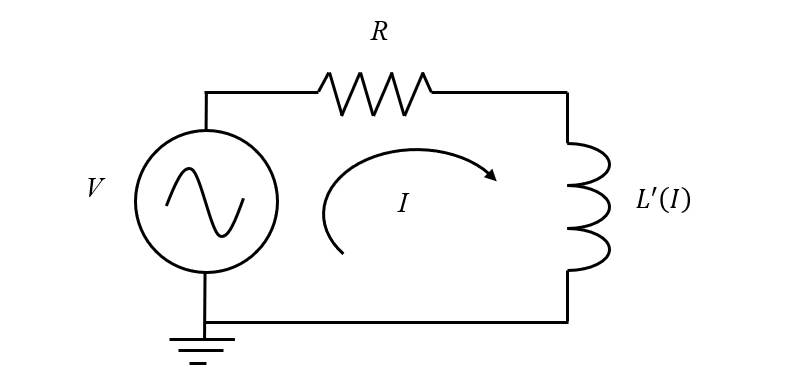
電流の関数としての差動インダクタンスを持つ非線形インダクターの等価電気回路モデル.

この差動インダクタンスがわかったので, これを電気回路モデル内で使用して, 過渡的な動作を迅速に予測できます. 電気回路モデルには, デフォルトの接地ノード機能に加えて, 3つの機能のみが必要です:

• 抵抗 機能
• インダクター 機能
• 電圧源 機能

計算された コイル 抵抗に等しい抵抗を持つ 抵抗 機能を使用します. これと直列に, 以前に計算された微分インダクタンスを格納する 補間 テーブルで定義された非線形インダクタンスを持つ インダクター 機能を追加します. この非線形インダクタンスは, 電流の絶対値の関数にすることができます. 非線形動作は電流の符号に依存しないからです. 最後に, 電圧源 機能を直列に配置できます. これら 3 つの機能を組み合わせることで, 応答を予測できる集中モデルが作成されます. この集中モデルの結果は, 有限要素モデルと比較できます. 最初の数周期では, モデルはまだこの非線形システムの周期的な定常応答に近づき始めたばかりであることに注意してください.

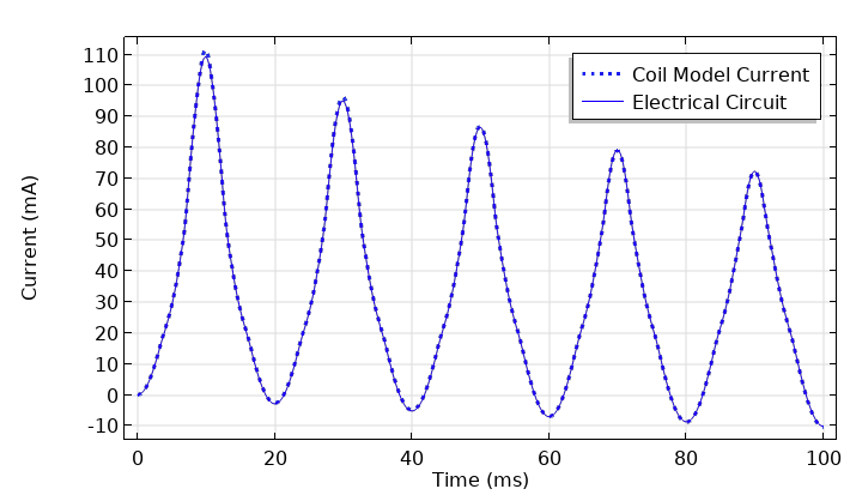
AC 電圧源を適用したインダクターを流れる電流のグラフ. 電気回路モデルと磁場モデルの結果は一致しています.

これらの時間領域データは, フーリエ変換して周波数領域にすることもできます. これにより, 材料の非線形性によって生じる高調波をより明確に識別できます. 電気回路モデルはすぐに解決できるため, さまざまな動作条件をすばやく調べることもできます. 予想どおり, デバイスが非線形領域に駆動されると, 高周波成分が増えます.

 
ピークツーピーク電圧の増加に伴う電流の周波数内容のプロット.

磁石でバイアスされた非線形インダクター

説明のため, 上記の例を変更して, コアの隣に磁石を配置します. この磁石はコイルの連結磁束に寄与し, 非線形材料にバイアスをかけます. 差動インダクタンスは, 印加電流の大きさと符号の両方に依存します. セカントインダクタンスには連結磁束への磁石自体の寄与が含まれますが, この時間不変の磁束は逆誘導電圧には寄与しないことに注意してください. 磁石は, 存在する非線形材料の B-H 関係を変更するようにのみ機能します. つまり, 磁石は線形材料のみで作られたインダクターの応答には影響しません. ただし, 磁石は常にセカントインダクタンスにバイアスを導入することを念頭に置いておくことが重要です. したがって, モデルに磁石が存在する場合は, すべての材料が線形であっても, 常に差動インダクタンスを使用することをお勧めします.

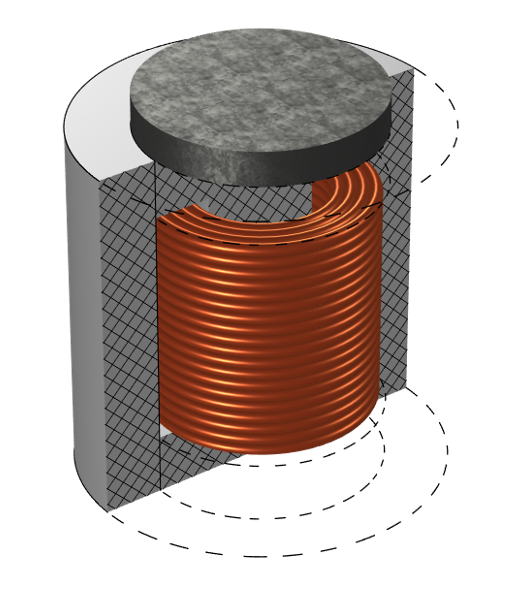
BH 非線形コアの上に磁石を置くと, 応答にバイアスがかかります.

 
このバイアスインダクターの差動インダクタンスは, DC 電流の符号に対して非対称です.

この差動インダクタンスは, 電気回路モデル内でも使用できます. この場合も, 起動期間を除いて結果が非常によく一致することがわかります. 起動期間でのこの不一致は, 集中モデルと比較した, 空間的に変化する場とコアの飽和の空間的変化を計算するモデルの違いを強調しています.

 
空間有限要素モデルとバイアス差動インダクタンスを備えた集中回路モデル間の一致.

変圧器の非線形応答

次に, 合金粉末コアフェライト製のコアの周りに巻かれた 2 つの同一コイルで構成される変圧器を見てみましょう. 対称性は, モデルサイズを縮小するだけでなく, L’_{11} = L’_{22} および L’_{12} = L’_{21} であるため, 計算に必要なデータ量を削減するためにも利用できます. ただし, 一般的なケースでは, 差動インダクタンスは, この対称構造では L'(I_1,I_2) = L'(|I_1+I_2|,0) である I_1 (一次側の電流) と I_2 (二次側の電流) の両方の関数になることがあります. つまり, 2 つの変数をスイープするのではなく, I_2=0 を維持しながら, I_1 の範囲で差動インダクタンス L’_{11} と L’_{12} を計算するだけで済みます.

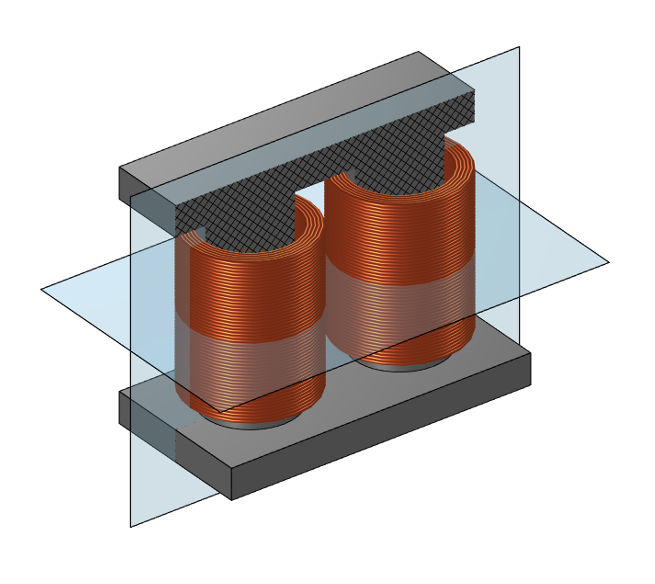
対称コアの周りに巻かれた2つの同一コイルで構成された変圧器. 2 つの対称面が可視化されています.

これら2 つの差動インダクタンスが計算されると, 一連の関数を使用して相互インダクタンス行列の 4 つの項がすべて定義されます. これらの項は, 同じトランスの電気回路モデル内で使用できます. 非線形性のため, 2 つのコイル間の結合は, 次の図に示すように, 電流制御電圧源機能を使用してモデル化されます.

 
非線形コア材料を使用した変圧器の等価回路.

完全な 3 次元モデルを使用してこの変圧器の応答を解くには, かなりの計算コストがかかりますが, 電気回路モデルを解くのは非常に高速です. 結果はここでも非常によく一致していますが, 微分インダクタンス行列は, 考えられるすべての動作条件で計算することが重要です. 微分インダクタンス行列を計算するためのこの 1 回限りのコストは, バッチスイープまたは クラスター スイープを介して並列化でき, 利用可能なすべての計算リソースを活用できます.

 
一次側に正弦波の AC 電圧をかけると, 一次側と二次側に非線形の電流が流れます. 一次側の電圧と二次側の電流を, フルモデルと電気回路モデルで比較します.

ソレノイドの動的応答

次に, 鉄製のハウジング内のコイルと鉄製のプランジャーで構成されたソレノイドを見てみましょう. プランジャーは, 軸に沿ってのみ移動できるように取り付けられています. 鉄の透磁率は予想される磁場の範囲で一定であると仮定し, 材料の非線形性は無視します. また, ハウジングとプランジャーは絶縁材料で結合された部品で構成され, 軸の周りを循環する誘導電流を最小限に抑えると仮定し, 鉄を損失のないものとして扱います.

鉄製のハウジング内のコイルと, バネによって所定の位置に保持された鉄製のプランジャーで構成されるソレノイド.

スプリングは, ハウジングの外側でプランジャーを平衡位置に保持します. コイルに電圧が加えられると, 電流が流れ始め, プランジャーを中央に向かって押します. この状況では, 物質的な非線形性はないため, 連結された磁束は時間とともに変化する電流 I に線形に依存しますが, プランジャーの Z 位置 u によって非線形に変化します:

したがって, 連鎖則により, 逆誘導電圧は:

最初の項は, プランジャーの位置が変わるとセカントインダクタンスが変化するという事実を説明します. 2 番目の項は, プランジャーが非ゼロの磁場を速度 \dot{u} で移動するときに, 追加の逆誘導電圧を導入します.

連結磁束は印加された直流電流I_{DC}と線形であることに留意し, 直流電流が印加されたときの位置に関して最初の式を微分すると, 次の式が成り立つことがわかります:

したがって, 位置に関する微分を計算するには, 感度インターフェースと移動メッシュインターフェースを組み合わせて, 固定DC電流でのZ位置の微小変化\deltaに関する連結流束の偏微分を計算します:

移動メッシュ を使用して, Z 位置の有限および微小な変化を導入し, プランジャーストロークに沿ってさまざまな位置 u の範囲をスイープしながら, 微小な変位 \delta に関してのみ偏微分を取得します. この偏微分により, 回路モデルをプランジャーの運動方程式に結合する単純な電気機械集中モデルを構築できるようになります.

 
電気機械集中モデルは, 力, 位置依存のセカントインダクタンス, およびプランジャーが動いているときの逆誘導電圧によって結合された回路モデルと集中機械モデルで構成されます.

集中系のスケッチからわかるように, 電気系は力を介して機械系と結合します. 力の式がどのように得られるかを理解するために, 電流とプランジャーの位置によって変化する系内の総磁気エネルギーの式を見てみましょう:

プランジャーにかかる全力は仮想仕事法で求めることができる. 線形磁性材料の場合, 軸方向の力は, 全磁気エネルギーを微小変位に対して偏微分することで求められます:

つまり, 力はコイルを流れる電流と位置に関するインダクタンスの偏微分関数であり, これはすでに計算済みです. したがって, ソレノイドのモデルとともに, プランジャーの位置に関する常微分方程式も同時に解きます:

ここで, u_0 はプランジャーの平衡位置です. この方程式は, 別の グローバル ODE および DAE インターフェース, または任意の物理インターフェースに追加できる グローバル方程式 機能を介して解くことができます. したがって, この方程式は, 磁場 インターフェースの解と組み合わせて運動を解くために使用でき, 電気回路 インターフェースと組み合わせて解くことができます.

プランジャーを軸に沿って自由に振動させ, 興味深いダイナミクスを生成する一連の入力の観点から結果を調べ, 集中モデルが集中パラメーターの計算に使用される空間モデルと非常によく一致することを示します.

 
ソレノイドの磁場の詳細モデルと集中モデルの比較.

独自の集中モデルの構築

ここでは, COMSOL Multiphysics^® ソフトウェアの機能を強調した 4 つの例を見てきました. このソフトウェアは, 微分インダクタンスだけでなく, コイルの連結磁束の他の入力変数に対する導関数も抽出します. 結果の量は, システムパフォーマンスの優れた予測子となる軽量の集中モデルの構築に使用できます.

差動インダクタンスを抽出して, このような集中モデルを構築したいですか? アプリケーションギャラリからこれらの例をダウンロードしてください:

参考文献

1. 1. D. Cheng, “Field and Wave Electromagnetics”, 2nd ed., Addison-Wesley, 1991