
COMSOL Multiphysics® ソフトウェアのアドオン製品である RF モジュールの遠方場ドメイン機能を使用して, 任意の散乱体またはアンテナの遠方場応答を測定できます. さらに一歩進めるために, COMSOL Multiphysics® は実験設定をより広範囲に再現できます. 有限要素法と境界要素法 (FEM–BEM) のカップリングのおかげで, EMI/EMC 問題に対処する際の, 回路基板のアンテナゲイン測定や回路基板の放射やエミッションまたは耐性テストを実施することができます. このカップリングは, マイクロストリップパッチアンテナモデルの周囲の無限の自由空間での波の伝播を見つけるために使用することもできます. このブログでは, FEM–BEM カップリングのアプリケーションの 1 つであるLOS通信用の送信機アンテナと受信機アンテナのモデリングについて詳しく説明します.
LOS通信
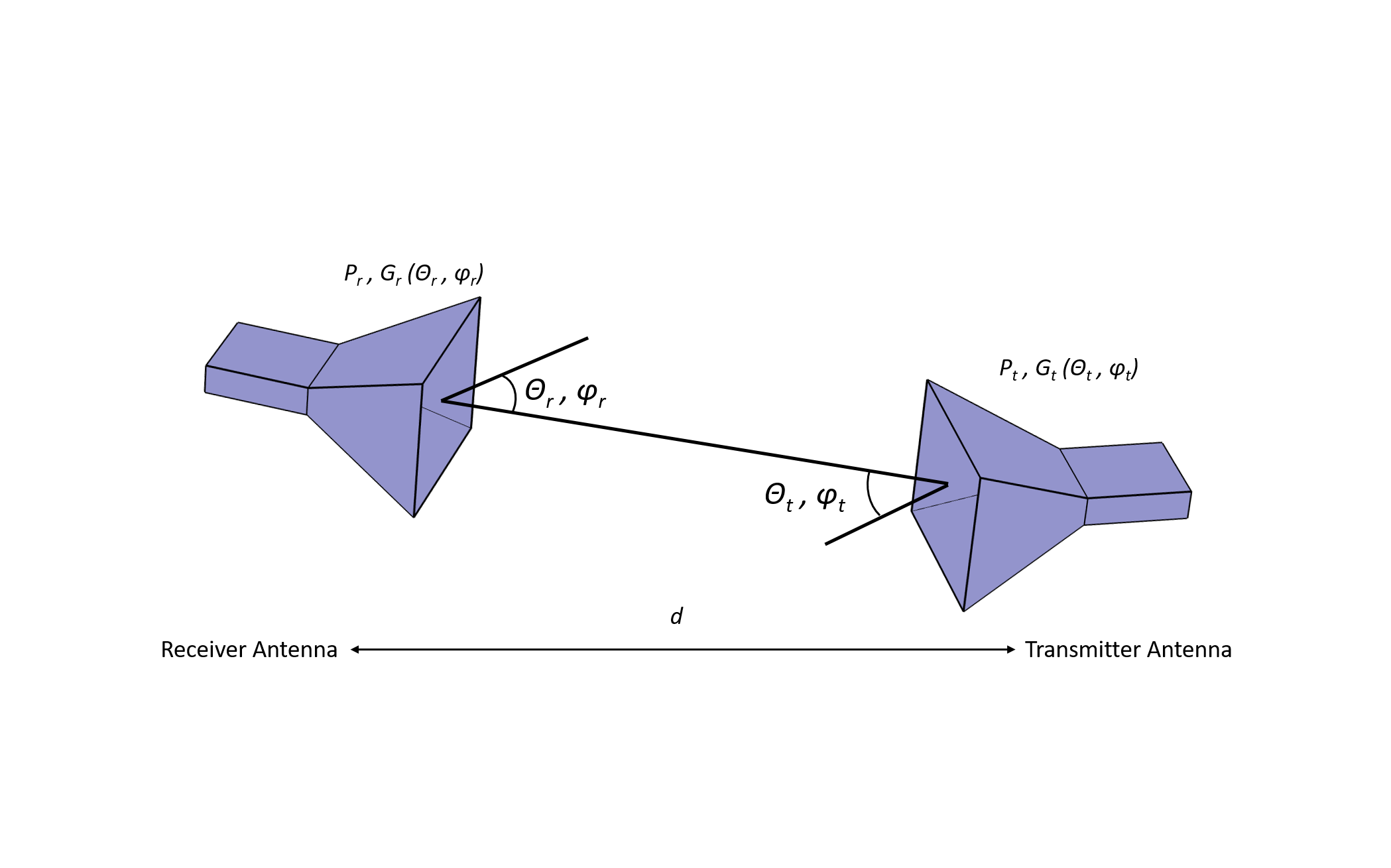
LOS 通信を理解するには, アンテナが電力をどのように受信するかを知ることが重要です. これは, 次のようなよく知られたFriisの伝達公式 (dB 単位) によって与えられます.
ここで, \text {P}_\text{t} は送信電力; \text{P}_\text{r} は受信電力; \text{G}_\text{t} (\theta_t, \phi_\text{t}) および \text {G}_\text{r} (\theta_\text{r}, \phi_\text{r}) はそれぞれ送信アンテナおよび受信アンテナのゲインで; \text {Path Loss} (in dB) は次で与えられます.
{\lambda} は動作波長, d はアンテナ間距離です. この距離は通常, フレネルゾーン内のアンテナ間の最短距離を表します. (このゾーンはアンテナ間に形成される楕円形の領域であり, 信号の伝送を妨げる可能性のある物理的な障害物は含まれません. )
さて, 式を整理してみましょう. これにより, シミュレーションを使用して, 新しい方程式 (方程式 3) の右辺とシミュレーションから得られた S パラメーターを比較できます. この方程式は次のとおりです.
ここで, 左側は S21 (単位は dB) を表します.
送信アンテナと受信アンテナのモデリング
Friis の公式から, パス損失を最小限に抑えることで \text {P}_\text{r} を最大化できることがよくわかります. 動作周波数や送信機と受信機のアンテナ間の距離が増加すると, 経路損失が増加します. 図 2 は, 送信機と受信機が FEM ドメインでモデル化され, 事前定義された FEM-BEM 結合と結合されていることを示しています. 送信機はマイクロストリップパッチアンテナであり, 電磁波 (周波数領域) 3: Tx および Rx アンテナ (emw3) インターフェースの集中ポート 1 電圧励起がオンになっていることに注意してください ( emw3 インターフェースとも呼ばれます). 受信機はYagi–Uda アンテナで, emw3 インターフェースの集中ポート 2 励起がオフになっています.
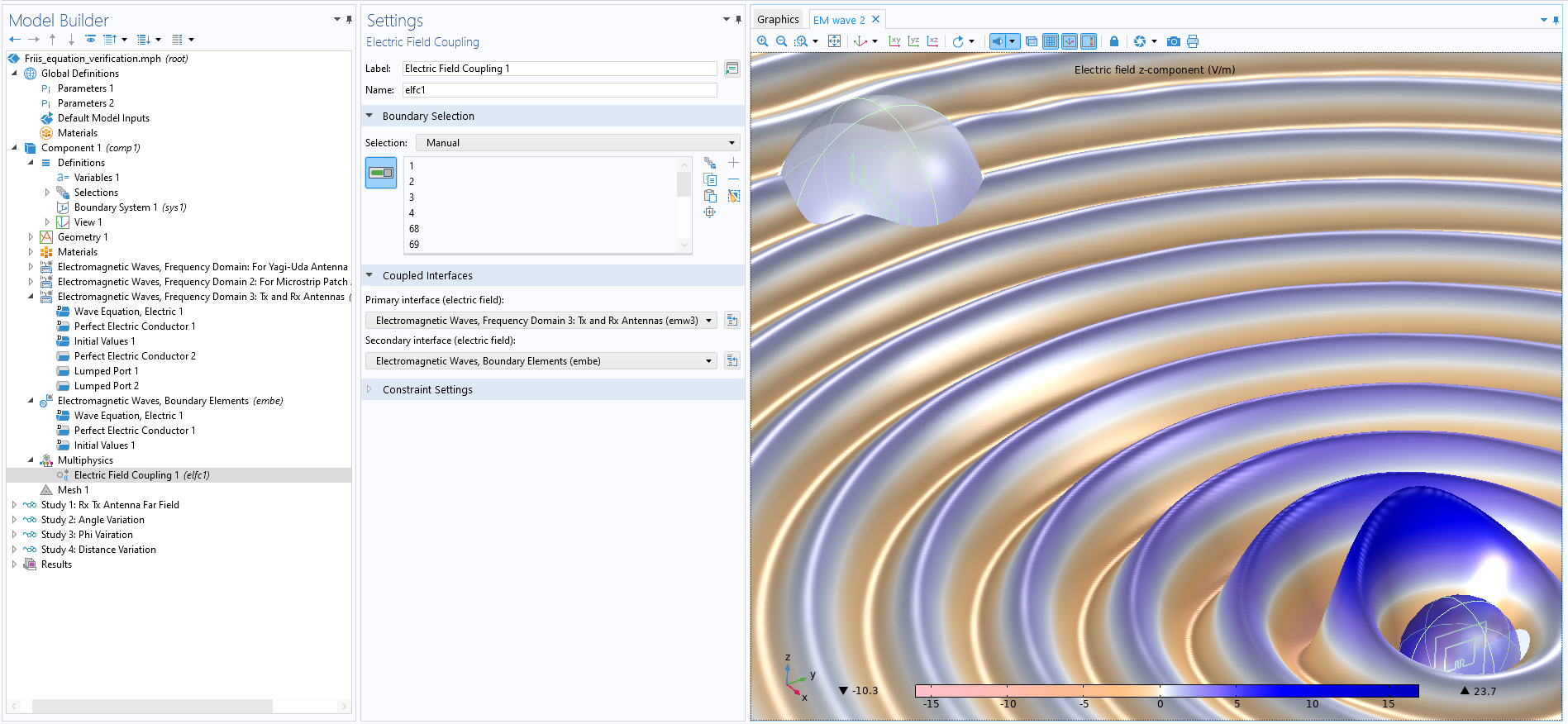
図 2. emw3 および embe インターフェースは, 電場カップリングマルチフィジックスインターフェースとカップリングしています.
また, アニメーション機能 (以下を参照) を使用して, 送信機から受信機への波の伝播を可視化することもできます.
送信機から受信機への電磁波の伝播. このシミュレーションでは, FEM–BEM カップリング機能を使用します.
Friis の式では, 両方のアンテナの遠方場アンテナゲインが必要です. これらは, 次の遠方場ドメインノードを使用して計算されます.
- >電磁波 (周波数領域): Yagi–Udaアンテナ (Rx) (emw) インターフェースの場合 – 略してemw インターフェース
- 電磁波 (周波数領域2): マイクロストリップパッチアンテナ (Tx) (emw2) インターフェースの場合 – 略してemw2 インターフェース
以下の画像でそのようなインターフェースを確認できます.
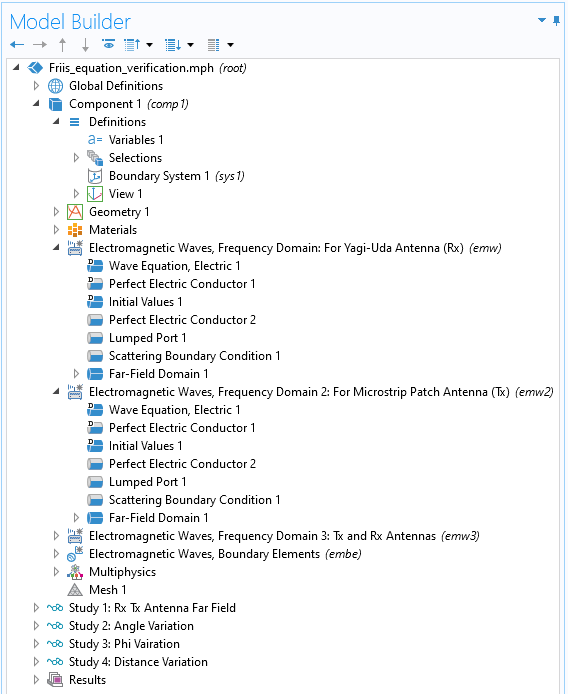
図 3. emw および emw2 インターフェースは, Yagi–Udaおよびマイクロストリップパッチアンテナの遠方場ゲインを見つけるために使用されます.
比較のために, Friis の公式を定式化するための変数が作成されます (図 4). アンテナ間の距離が増加し, S パラメーターの観点から受信電力が測定されます (図 5).
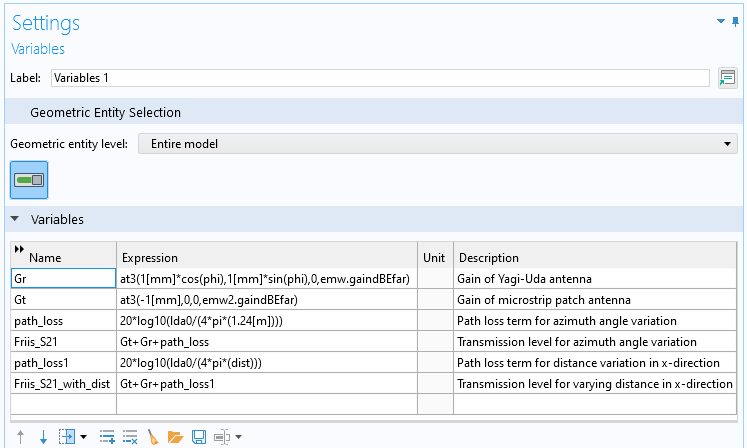
図 4. 遠方場式を使用してFriis方程式を定式化します. ここで, lda0 と dist は, それぞれ動作自由空間波長と Rx アンテナと Tx アンテナ間の距離を表します. phi 角度パラメーターで定義された特定の座標で遠方場ゲインにアクセスするには, 事前定義された at3() 関数が使用されます.
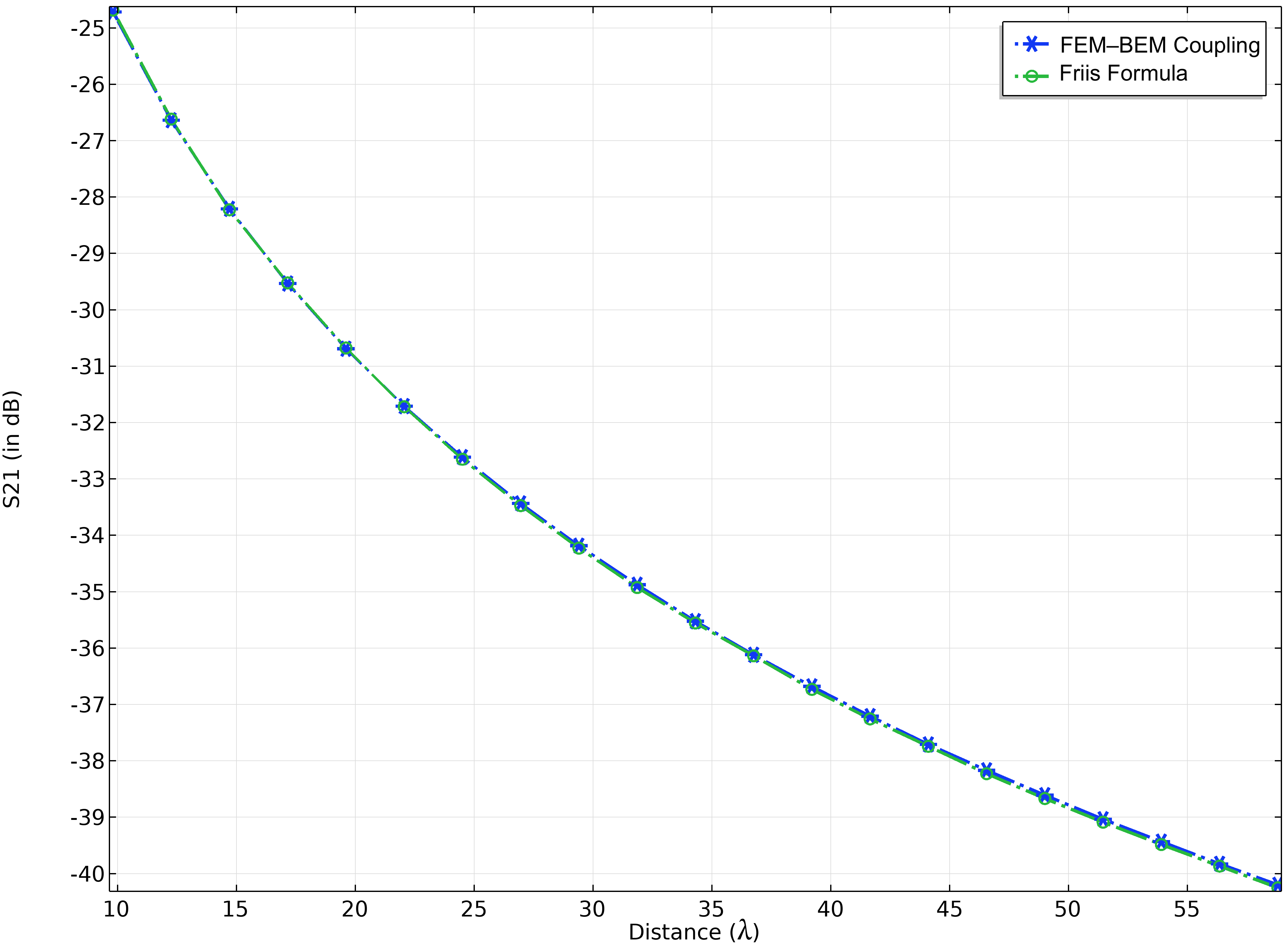
図 5. Friis の公式とさまざまな距離での受信電力の比較.
さらに, \text {P}_\text{r} は, アンテナ放射パターンのメインローブを揃えることによって増やすことができます. 受信アンテナを方位角で回転させてこれを確認してみましょう. この角度の変化は, -90° から 90° までになります. 言い換えれば, アンテナゲイン測定設定を模倣していることになります. 図 6 から, 受信電力は 0° で最大に達することがわかります. この構成は, x 軸に沿って最大ゲインを持つ両方のアンテナに対応します.
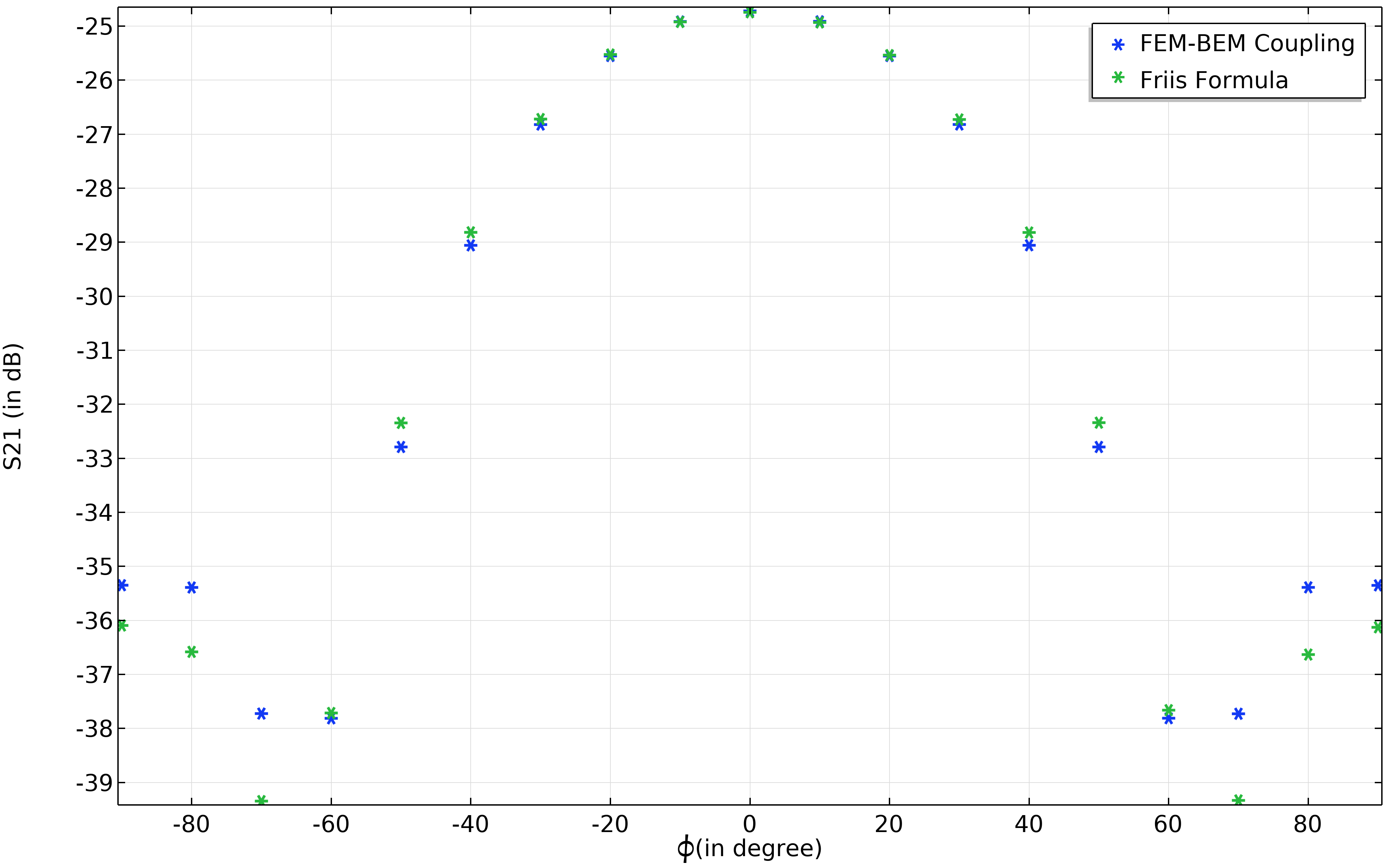
図 6. さまざまな角度での受信電力と Friis の公式の比較.
EMI/EMC 試験へのドアを開く
波動光学モジュールで利用できるビームエンベロープ法は, 非散乱電磁波問題における波長同等のジオメトリサイズの障壁を克服し, 誘導媒体に最適です. ただし, メッシュ要件やジオメトリサイズの制限に対処することなく, FEM–BEM カップリングを使用して散乱 EM 問題をモデル化することもできます. そのようなアプリケーションの 1 つは, EMI/EMC テストベンチの設定です. たとえば, RE102 軍用規格 (最大 18 GHz の周波数) の放射テストを実行するには, テスト対象デバイス (DUT) とアンテナの間の距離は 1 メートルです. 18 GHz の信号の場合, 1 メートルの距離は波長の 60 倍に相当し, FEM を使用してこのような広大な空間をモデル化すると, 計算コストが非常に高くなります. 図 7 に示すように, DUT とアンテナを単一の FEM でモデル化する代わりに, それらを 2 つの FEM ドメイン (もちろん同等の波長サイズ) に分離し, BEM と結合することができます. アンテナで検出される電力は, DUT から放射される EM 信号強度の測定値となります.
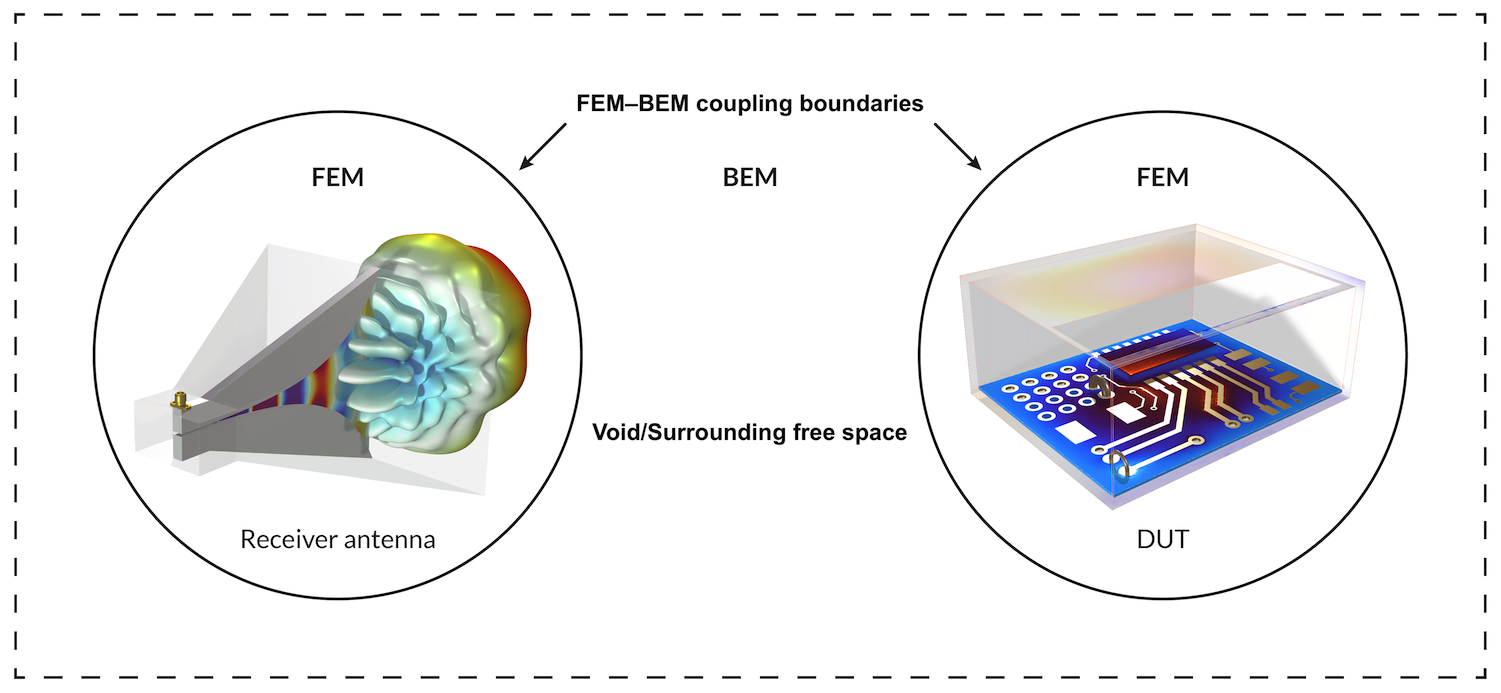
図 7. 放射解析を実行するための EMI/EMC テストベンチ設定の図.
終わりに
FEM と BEM のカップリングにより, メッシュ要件や計算リソースの制限により制限されていた広範な EM シミュレーションへの扉が開かれました. Friis 伝送方程式を検証すると, ユーザーが DUT の EMI/EMC 解析におけるエミッションおよび耐性試験に関心があるシミュレーションの場合, 信頼性が高まります.
次のステップ
下のボタンをクリックすると, アプリケーション ギャラリに移動します. FEM–BEM カップリングを使用したフリス伝送方程式の検証チュートリアルモデルを自分で試してみてください:
(ヒント: さらにモデリングの練習が必要ですか? マイクロストリップパッチアンテナの FEM–BEM カップリング をご覧ください.)






コメント (0)