風が吹く浜辺の砂, 遠くの星の渦, 熱帯魚の皮膚. 私たちはどこを見ても, 自然界のパターンを目にすることがあります. 一見ランダムに見える要素や力の組み合わせから, ある条件下で複雑なデザインが生まれることがあります. このような形態形成のプロセスは, 生物でも無生物でも観察することができ, 場合によっては反応拡散方程式で記述することができます. ケミカルモデリングによって, チューリングパターンの出現の背後にある条件をシミュレートすることができ, 視覚的に驚くべき結果を見ることができます!
自己触媒反応からチューリングパターンまで
キュービック自己触媒反応: 化学反応工学モジュールを使って開発されたチュートリアルモデルのグレイ・スコットモデルは, 反応拡散方程式によって支配される自己触媒化学反応の効果をシミュレートするものです. ここでは, 簡単な自己触媒反応の例を示します:
A + B → 2B
物質 A と物質 B の存在によって反応が促進される場合, 物質 A がなくなるまで物質 B が生成されます. 物質 A が減少する一方で物質 B の相対的割合が上昇すると, 混合物全体がその領域内で拡散します. この動き, つまり拡散は直線的なものではありませんが, 完全にランダムなものでもありません. 1952年に発表した論文 “The Chemical Basis of Morphogenesis” (参考文献1) で, このプロセスを説明した偉大な数学者アランチューリングの名をとって, チューリングパターンと呼ばれるデザインを作成します.

自然界に数多く存在するチューリングパターンの一つを示す巨大フグの皮膚. 画像: Chiswick Chap, licensed under CC BY-SA 3.0, via Wikimedia Commons.
多安定反応拡散系のグレイ・スコットモデル
もし, 自己触媒反応-拡散系をさらに非線形にするとどうなりますか? 1980年代, P. Gray と S.K. Scott (参考文献2) の研究者は, より速く加速する反応の挙動を研究しました:
A + 2B → 3B
Gray と Scott は, この系の条件として, 物質 B が時間とともに減衰することを付け加えました. 彼らの研究は, これらの条件が反応拡散プロセスに多安定性を示す原因となることを発見しました. これは, 動的プロセスが平衡を達成し, A と B の量と分布がほぼ安定することを意味しますが, それはほんの一瞬です. 系は, 安定性と急速で複雑な空間拡散の期間の間で振動し始めます. この現象は現在, Gray と Scott にちなんで名付けられており, その作用は化学, 物理学, 生物学で観察されています.
COMSOL Multiphysics® によるグレイ・スコットモデルのシミュレーション
自己触媒チュートリアルモデルでは, グレイ・スコットモデルによるシミュレーションを構築することができます. 反応-拡散プロセスのパラメーターを設定し, その効果のアニメーションを生成することができます. これらのアクションは, 周期的な境界条件を持つ矩形場を記述するユーザー定義の 2D コンポーネントで行われます. このコンポーネントは, 化学反応容器に入った試薬が完全に混合されることを想定した理想的な連続攪拌槽反応器 (CSTR) をベースにしています. 反応は, CSTR 内部で相互作用する均一濃度の物質 A と物質 B を添加することから始まります.
以下のアニメーションは, 物質 A と物質 B の初期濃度と, それらが時間の経過とともにどのように変化するかを示しています. 2つの物質は並んで表示されますが, 実際には同じ領域に混在していることに注意してください. 反応は, 混合 A と B の CSTR への流入から始まります. 流入速度は, 10個の等距離の値にわたってスイープされるパラメーター k によって記述されます. このスイープにより, 流入速度が反応拡散プロセスの動作にどのように影響するか, およびそれが作成するパターンを特定できます. これは, 0.0609 /s の流入によって引き起こされる反応のアニメーションです:
0.0609 /s の試薬の流入により, 物質 A (左) と物質 B (右) の量と分布が変化する様子をアニメーション.
この速度で流入すると, 2つの物質の分布は急速に変化し, その変化率は横ばいになります. k の値がパラメータースイープに沿って変化すると, 反応の挙動も興味深いように変化します. 下のグラフは, 10種類の k の値について, これらの変化を示しています.
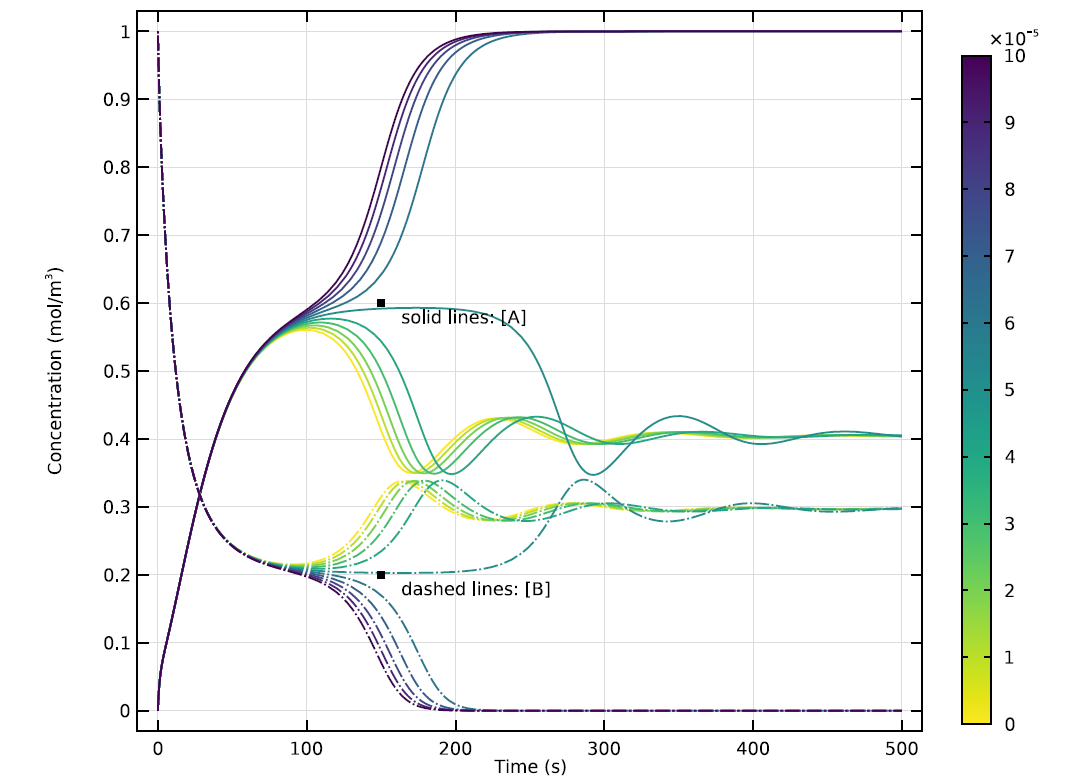
モデルの 0D バージョンにおける A と B の濃度の時間発展, k の10の異なる値の結果を示しています. k のいくつかの値での反応の波形の見かけの振動に注意してください.
k の特定の値では, A と B の濃度はすぐに安定した平衡を達成します. 他の値では, 反応が A と B が共存できる状態に向かって進行するため, 遷移振動が発生します. この比較的安定した状態は, 均一にはほど遠いかもしれませんが…
0.0611 /s の試薬の流入により, 物質 A, B の量と分布が変化する様子をアニメーションで表現.
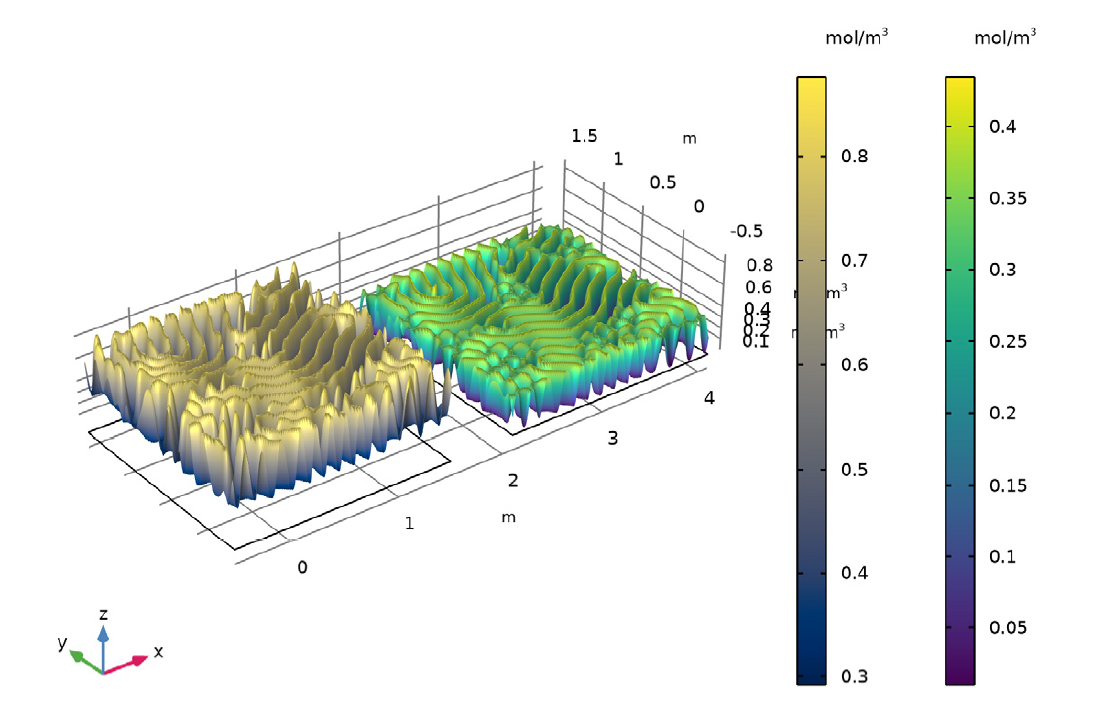
k = 0.06011 の試薬の流入により, 物質 A と B の量と分布が変化する様子を示すアニメーション.
上記のアニメーションや画像に見られるように, 反応拡散過程では, 適切な条件下で壮大なチューリングパターンを生成することができます.
あなた自身のチューリングパターンを調整する
宇宙に秩序をもたらす形態形成過程を探求する準備はできましたか? あるいは, クールなアニメーションを作りたいですか? いずれにせよ, キュービック自己触媒をダウンロードすることで始めることができます. COMSOL Multiphysics ソフトウェアのアニメーションプレーヤーの実行方法を含むチュートリアルモデルを, 下のボタンからダウンロードしてください.
参考文献
- A.M. Turing, “The Chemical Basis of Morphogenesis,” Phil. Trans. R. Soc. Lond. B, vol. 237, pp. 37–72, 1952.
- P. Gray and S.K. Scott, “Autocatalytic Reactions in the Isothermal Continuous Stirred Tank Reactor, Oscillations and instabilities in the system A + 2B=>3B; B=>C,” Chemical Engineering Science, vol. 39, pp. 1087–1097, 1984.



コメント (0)