
構造力学解析を行う際には, 幾何学的非線形性の概念に必然的に遭遇することになります. このブログでは, 幾何学的非線形性とは何を意味するのか, そしてどのような場合にこの影響を考慮すべきなのかについて説明します.
幾何学的非線形性
構造力学の基礎コースでは, 幾何学的非線形性は明示的には紹介されないこともあります. 実際, 幾何学的線形性が暗黙のうちに前提とされていることがよくあります. 幾何学的に線形な設定では, 釣合い方程式は変形前の状態で定式化され, 変形によって更新されることはありません. 構造力学は変形を計算することを目的としているため, 最初は少し不安に感じるかもしれません.
しかし, ほとんどの工学的問題では, 変形は非常に小さいため, 元の形状からのずれは知覚できません. 変形を無視することで生じる小さな誤差は, より高度な理論によって生じる数学的な複雑さを正当化するものではありません. そのため, ほとんどの解析は幾何学的線形性を前提として行われます.
変形を無視できない場合は数多くあり, それらのすべてが直感的に大きな変形であると判断できるものではありません.
幾何学的非線形性を考慮することによる影響
COMSOL Multiphysics で幾何学的非線形性を考慮する場合, 数学的な解析に最も大きな影響を与えるのは以下の点です:
- 空間 座標系と 物質 座標系は区別されます. ある点の空間座標 (\mathbf x) は, 同じ点の物質座標 (\mathbf X) とは変位ベクトル (\mathbf u) だけ異なります. つまり, \mathbf x = \mathbf X + \mathbf u となります. したがって, 式では座標名を大文字と小文字のどちらで使用するかが重要になります.
- ひずみは, 工学ひずみではなく, グリーン・ラグランジュひずみテンソルで表されます.
- 応力は, 第2ピオラ・キルヒホッフ応力テンソルで表されます.
- 圧力荷重は変形を考慮します. 境界の法線が更新され, 伸張による面積の変化も考慮されます.
様々な応力テンソルとひずみテンソルの詳細については, こちらの 以前のブログ をご覧ください. ただし, ここでひずみの測定方法について少し触れておきたいと思います. そこで, ひずみテンソルのいくつかの要素を検討することで, 線形ひずみと完全な非線形ひずみの違いを見てみましょう.
X 方向のグリーン・ラグランジュ法線ひずみは次のように表すことができます.
二次項を省略すると, 一般的な工学ひずみが得られます:
同様に, せん断ひずみの場合, グリーン・ラグランジュひずみ成分は次のように表されます.
ここでも, 工学ひずみは非線形項を無視することで得られます:
大きな回転, あるいはそれほど大きくない回転
構造物が大きく回転すると, 基礎理論で用いられる工学ひずみはもはや有用な表現ではなくなります. 剛体の回転は, 工学ひずみテンソルの非ゼロ成分を引き起こします. これは, 構成則を通して, 物理的な理由から剛体には現れないはずの応力を引き起こします. 別の見方をすれば, 有用なひずみテンソルは, 剛体の運動において伸張や相対角度の変化がないという事実を反映できなければならないということです.
xy 平面内で原点を中心に剛体回転する2次元物体を考えてみましょう. 長方形鋼板を 10° 回転させた単純な線形平面応力モデルを以下に示します.
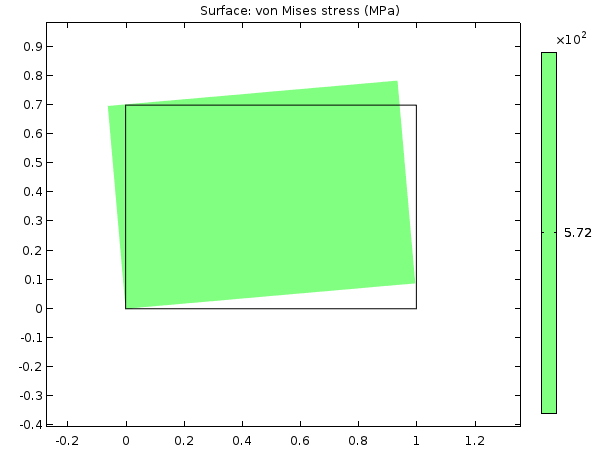
幾何学的非線形性のない長方形鋼板を 10° 回転させた場合の等価応力.
結果として, 等価応力は 572 MPa となり, これは最も一般的な鋼材の降伏限界を超えています. なぜこのような結果になったのかを理解するには, 解析解を検討してみましょう:
元々 (X,Y) に配置されていた点は, 新しい位置 (x,y) に移動し, 次の式で表されます.
x = X \cos(\phi)-Y \sin(\phi) \\
y = X \sin(\phi) + Y \cos(\phi)
\end{matrix}
つまり, 変位 (u,v) は
u = x-X = X (\cos(\phi)-1)-Y \sin(\phi) \\
v = y-Y = X \sin(\phi) + Y (\cos(\phi)-1)
\end{matrix}
この場合, 工学的ひずみは
\epsilon_X = \frac{\partial u}{\partial X} = \cos(\phi)-1 \\
\epsilon_Y = \frac{\partial v}{\partial Y} = \cos(\phi)-1 \\
\epsilon_{XY} = \frac{1}{2}(\frac{\partial u}{\partial Y}+\frac{\partial v}{\partial X}) = -\sin(\phi)+ \sin(\phi) = 0
\end{array}
剛体の回転では, すべてのひずみはゼロになるはずですが, 明らかにこれらのひずみ成分のうち2つはゼロではありません. 金属は 0.001 程度のひずみで降伏することがよくあります. この大きさの架空のひずみは, 2.5° の回転ですでに発生します. ひずみを 0.0001 未満に保つには, 0.8° を超える剛体回転があってはなりません. これは, たとえ “小角度近似” で十分であると予想される角度であっても, 幾何学的に非線形なアプローチを用いる必要があることを意味します.
上記と同じ剛体回転を用いますが, 代わりにグリーン・ラグランジュひずみを用いると, 次の式が得られます
このひずみテンソル成分は, 回転のどの値に対してもゼロになります. この特性は, グリーン・ラグランジュひずみテンソル全体に対しても, また任意の回転に対しても示されます.
幾何学的非線形定式化を用いることで, こうした応力アーティファクトを回避できます. これは, 幾何学的非線形性を有効にして同じ問題を解くことで確認できます. 応力レベルは純粋な数値ノイズとなり, 降伏限界よりも12桁低くなります
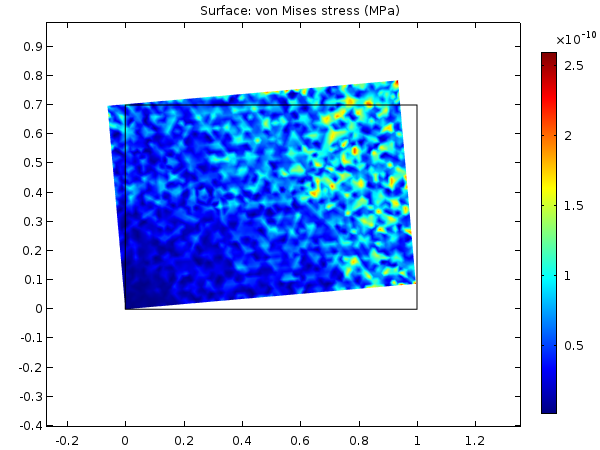
幾何学的非線形性を用いた場合の 10° 回転における等価応力.
薄肉構造の伸張
下のスケッチにある2本の梁について考えてみましょう:

端部条件が異なる梁.
右端では, 上側の梁は水平方向に自由に移動できますが, 下側の梁は移動できません. 線形理論では, 梁が垂直荷重を受ける場合, これら2つの端部条件は等価です. 軸方向と曲げ作用の間には連成はありません. しかし, 幾何学的に非線形な解析では, 異なる端面条件によって全く異なる結果が生じます:
- 端部が軸方向に自由に移動できる場合, 梁の垂直変位は幾何学的に線形の場合とほぼ同じです.
- 軸方向変位が拘束されている場合, 垂直変位は線形の場合よりも小さくなり, 荷重に対して強い非線形依存性を持ちます.
梁がたわむと, 端部が内側に移動できない場合, 梁の中心線が引き伸ばされます. これにより大きな軸方向力が生じ, 梁は張力を受けたワイヤーのような挙動を示します. つまり, 張力が大きいほど, 横方向の力に対する抵抗が大きくなります.
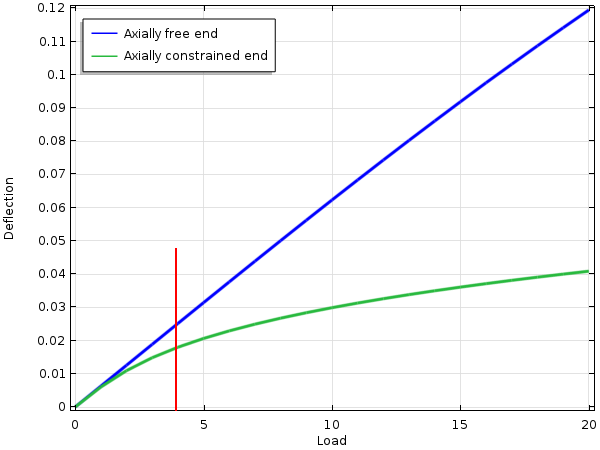
0.05 x 0.05 の正方形断面を持つ梁の中点たわみ. 赤い線は, 線形解析におけるたわみが 0.025 (梁の高さの半分) となる荷重を示しています.
同じ考え方は, 板やシェルにも当てはまります. 境界条件において, たわみによって面内張力が生じる場合, たわみが増加するにつれて板の剛性は著しく増加します.
経験則として, 線形解析における梁または板のたわみが厚さの半分を超える場合は, 幾何学的非線形効果を考慮する必要があるというものがあります. これは, 上の図の赤い線で示されています.
応力剛性
前の例で示したように, 構造物の剛性は, 幾何学的非線形効果によって大きく変化することがあります. これは 応力剛性 と呼ばれることもあります. この用語はやや誤解を招く恐れがあり, 剛性が低下する可能性もあるためです. 上記の梁に軸方向の圧縮荷重を加えると, 横方向の剛性は実際には低下します.
応力剛性は, 例えば遠心力によって大きな引張応力が生じる回転系において重要です. これにより, 系の固有振動数は回転数とともに増加します.
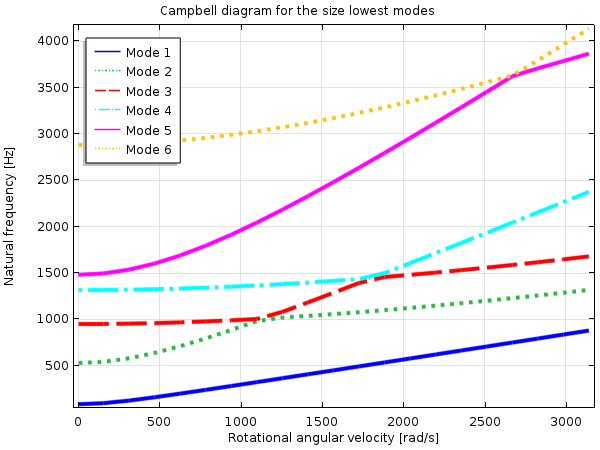
回転ブレードの固有振動数が回転速度によってどのように変化するかを示すキャンベル線図.
多くの場合, プレストレスを引き起こす荷重は, 実際に解析を実行する荷重とは異なります. そのため, 2つの異なる荷重系があり, それぞれを個別に解析する必要があることがあります.
COMSOL Multiphysics には, プレストレス系の解析に特化した2つのスタディタイプが定義されています:
- プレストレス解析, 固有振動数
- プレストレス解析, 周波数領域
プレストレスト構造の解析を目的としたスタディタイプ.
これらのスタディタイプは2つのスタディステップで構成され, ステップ1ではプレストレス状態を計算します. このスタディは線形または非線形です. 2番目のスタディステップ自体は線形ですが, 剛性マトリックスの設定時に幾何学的非線形性によって生じる非線形項を考慮します.
応力剛性が重要な例にご興味のある方は, 以下をご覧ください:
座屈
座屈, つまり荷重が特定の臨界値に達した際に安定性が失われる現象は, 幾何学的に非線形な効果によって引き起こされます. COMSOL Multiphysics には, 臨界荷重の一次近似を計算するための “線形座屈” と呼ばれるスタディタイプがあります.
線形座屈スタディタイプ.
線形座屈スタディでは, 固有値問題を解くことで近似的な座屈荷重が得られます.
代わりに, 崩壊点まで, あるいは崩壊点を超えて, 完全な非線形応答を追跡することもできます. この場合, 荷重を小さなステップで増加させる必要があります. この方法は計算コストが大幅に高くなりますが, 精度は向上します.
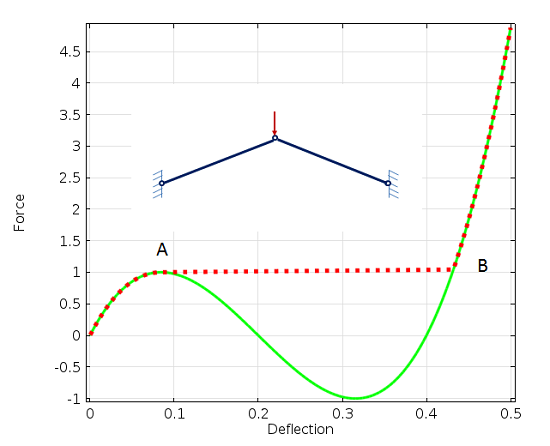
点 A での座屈崩壊を伴う荷重-たわみ履歴.
座屈の詳細については, こちらの 以前のブログ をご覧ください.
COMSOL Multiphysics における幾何学的非線形性の活用
幾何学的非線形性の有効化
幾何学的非線形性はスタディステップのプロパティです. 関連するスタディタイプでは, スタディ設定にチェックボックスが表示されます.
定常スタディの設定.
このチェックボックスは事前に選択されていて, 変更できない場合があります. 特定のフィジックスノードを追加した場合に発生します. 例えば:
- 超弾性材料
- 大ひずみ塑性
- 接触
非線形弾性やクリープなどのほとんどの非線形材料モデルは, 幾何学的非線形性を仮定していないことに注意してください.
幾何学的非線形性を持つ問題の解法
幾何学的に非線形な問題はしばしば強い非線形性を持つため, ソルバーの設定を行う際にはこの点を考慮する必要があります.
前述の固定端を持つ梁を考えてみましょう. 非線形問題を解く場合, 最初の反復後の解は線形問題の解と同じになり, 梁上のすべての点は横方向の荷重下で垂直方向にのみ移動します.
最初の反復計算後, 梁の軸方向の伸びが大きくなります. この伸びは軸力と関連しています. 正味の軸力は存在しない (その方向に外部荷重がかかっていない) ため, この力は次の反復計算の残差として残ります. この不均衡な力は, 適用された荷重よりも大きくなる可能性があります. 非線形ソルバーにとって, これは非常に厄介な問題に見え, ソルバーはしばしば減衰を導入します.
幸いなことに, これらの問題は数値計算で示されるよりも良好な挙動を示すことがよくあります. そのため, デフォルトよりも積極的な反復計算スキームを使用することで, 解の計算速度を大幅に向上させることができます.
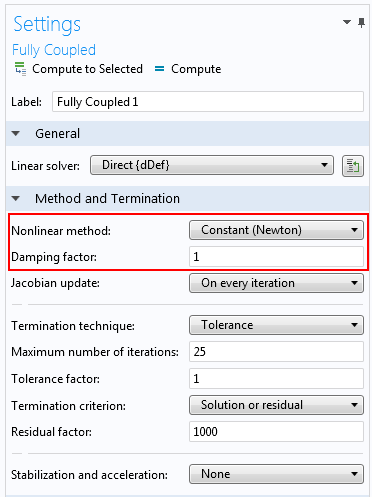
完全連成ソルバーの設定.
自動適応法ではなく定数ニュートン法を使用すると, ソルバーはより大きな更新を行います. 減衰係数は 1 (減衰なし) または 0.9 に設定できます.
幾何学的非線形性が唯一の非線形性の原因である問題は, ほとんどの場合, 特定の荷重レベルに対して唯一の解を持ちます. この意味で, 単一の荷重のみを用いた定常解析を用いて問題を解析することが可能です. 収束性の観点から, パラメトリック連続ソルバーを用いて荷重を徐々に増加させる方がよい場合があります.
高度に非線形な問題に対してソルバーを設定する方法の例は, Pinched Hemispherical Shell チュートリアルモデル に示されています.
まとめ
上記で示したように, 構造力学問題を解く際に幾何学的非線形性を考慮しなければならないケースがいくつかあります. 安全のために, この効果を常にモデルに組み込むのはなぜでしょうか?
- 非線形効果が非常に小さい場合でも, 非線形ソルバーを使用すると解析時間が大幅に長くなります. これは小規模なモデルでは問題になりませんが, 数百万自由度を扱う場合, 解析時間が半分に短縮されることは非常に重要です.
- 解析解と比較したい場合があり, そのような解は多くの場合線形理論に基づいています.
- 線形アプローチの使用を前提とする標準または解析手順に従う必要がある場合があります.
- 幾何学的に非線形な問題では, 実際の荷重を使用する必要があります. 構造応答の概念的な研究だけを行う場合, 推定された荷重が大きすぎると解が収束しない可能性があります.



コメント (0)