
COMSOL Multiphysics® ソフトウェアで変形オブジェクトをモデル化し, それらの間の距離を知りたいと思ったことはありませんか? このブログでは, 最近接距離場を決定する手法を用いて, オブジェクト間の距離を計算する方法を説明します. また, 距離場をマルチフィジックスモデルの一部として使用する方法についても説明します.
一般押出しコンポーネントカップリングを用いた距離計算
以下に示す, A と B というラベルの付いた2つのオブジェクトを考えてみましょう. 計算する3つの距離は以下のとおりです:
- 距離場としてオブジェクト A までの距離. この場合, オブジェクト A の周囲と内部にあるすべての点から, 境界上の最も近い点までの距離と方向 (dA) を計算します.
- オブジェクト B の境界上のすべての点から, オブジェクト A 上の最も近い点までの距離 (dAB).
- オブジェクト A と B 間の最短距離となる直線の端点 (dAB,min).
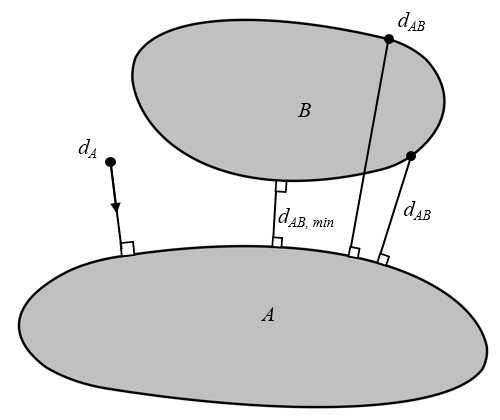
2つのオブジェクト A と B, そして計算する距離.
COMSOL Multiphysics では, 一般押出しコンポーネントと最小コンポーネントカップリングを組み合わせることで, これらの様々な距離をすべて計算できます. まず, 一般押出しコンポーネントカップリングの使い方を見てみましょう. 演算子に A_b という名前を付け, その ソース選択 をオブジェクト A の境界と定義します. 詳細 セクションで, メッシュ検索手法 として 最近傍点 を使用します. これらの設定を以下に示します. この演算子のその他の設定はデフォルトのままでかまいません.
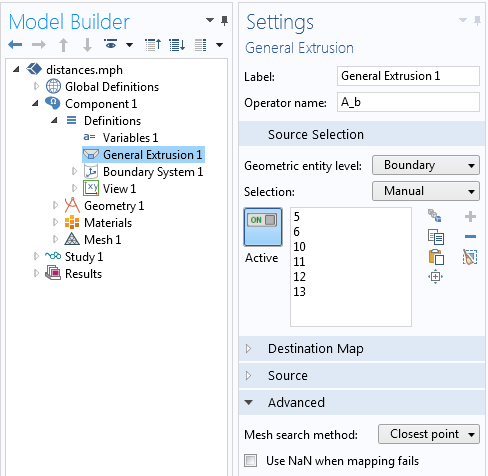
最近傍点の距離を計算するために使用される一般押出しコンポーネントカップリング設定. メッシュ検索手法 が 最近傍点 に設定されていることに注意してください.
この演算子は, 次のように定義される d_A という変数の定義内で使用します:
sqrt((x-A_b(x))^2+(y-A_b(y))^2)
この変数は, 距離場を計算したいドメイン (この場合は周囲ドメインのみ) に対して定義されます. この距離場 -\nabla d_A(\mathbf{x}) の勾配の負の値を計算することもできます. これにより, A の境界上の最近傍点を指すベクトル場の成分が得られます. 微分演算子 d(d_A,x) と d(d_A,y) を使用して, 下のスクリーンショットに示すように空間微分を求めることができます.
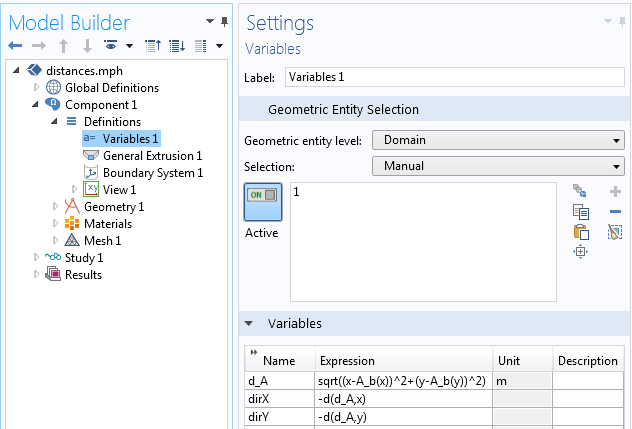
変数の定義.
これらの変数は, 好きな場所で使用できます. 例えば, 距離場をプロットしたり, 距離に応じて材質特性を設定したりできます. 下の画像は, 距離と方向ベクトルの等高線をプロットしたものです. オブジェクト B の背後のドメインでも距離が計算されていることに注意してください. ここでは明らかに多くの情報が得られますが, 周囲ドメインのすべての点で最短距離が計算されるため, 計算コストはかなり高くなります. これらの情報すべてが必要ではなく, オブジェクト間の距離だけが必要な場合もあります.
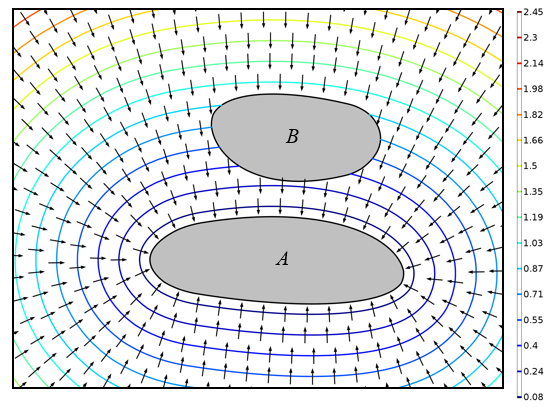
2つのオブジェクトを囲むドメインにおける距離場 (等高線) と, オブジェクト A の境界への最短方向 (矢印).
オブジェクト間のクリアランスの計算
少し簡単にするために, 2つのオブジェクト間の距離のみを考慮し, 方向は考慮しません. 同じ一般押出しコンポーネントカップリングを使用しますが, 距離を計算するには, オブジェクト B の境界に変数を定義するだけで済みます.
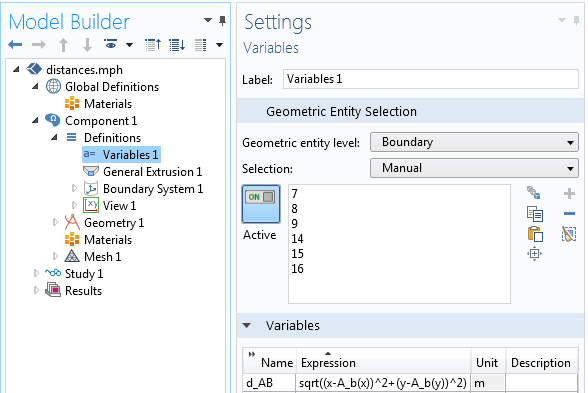
オブジェクト間の距離を定義する変数.
これは以前使用したのと同じ距離関数ですが, 中間空間にメッシュは必要ありません. ドメイン A と B にメッシュさえ必要ありません. オブジェクトの境界にメッシュがあれば十分です. このアプローチは計算時間が大幅に短縮されますが, オブジェクト A からオブジェクト B の境界上の各点までの最短距離しか得られません. 方向ベクトルを復元することはできません. これらの定義をすべて逆にして, オブジェクト B からオブジェクト A の境界上のすべての点までの最短距離を計算することもできます. 以下のプロットに示されているこれらの距離は, オブジェクトの境界に沿って利用できます.
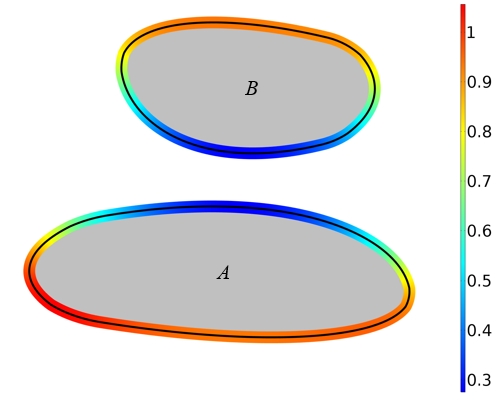
オブジェクト B の境界上のすべての点からオブジェクト A の最近傍点までの距離, およびその逆.
最小コンポーネント結合を用いたオブジェクト間の最短線の計算
では, 2つのオブジェクト間の最短距離を表す線を求めましょう. 前のセクションでは, A と B 間の最短距離を表す2つの変数, d_AB と d_BA を計算できることを説明しました. 今度は, これらのドメインの境界間の最短距離を求めます. そこで, オブジェクト A の境界用とオブジェクト B の境界用に, 2つの異なる最小コンポーネントカップリングを設定します. 以下のスクリーンショットに示すように, これらの演算子を minA と minB と呼びます.
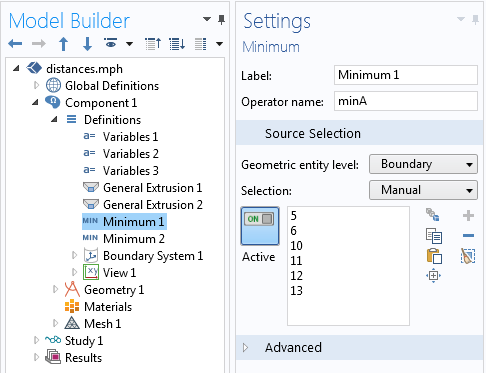
オブジェクト A の境界における最小コンポーネントカップリングの定義.
次に, これらの最小コンポーネントカップリングを呼び出して最短距離を抽出します. また, 最小コンポーネントカップリングに2つ目の引数を与えて, 距離が最小となる座標を見つけることもできます. 例えば, 変数 A_x を式 minA(d_BA,x) として定義すると, A の境界上で d_BA が最小となる x 座標の値を取ります.
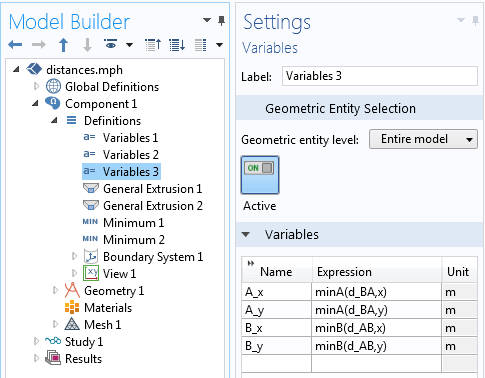
2つのドメイン間の最短線分の座標の定義.
これらの座標を定義する変数は, 任意の場所で呼び出すことができます. 例えば, 次の図に示すように, カットライン 機能を使用して, 2つのオブジェクトを結ぶ最短線分を表示できます. メッシュ化されたドメインと2つのオブジェクト間の解がある場合, 2つのオブジェクト間の最短線に沿って場をプロットできます.
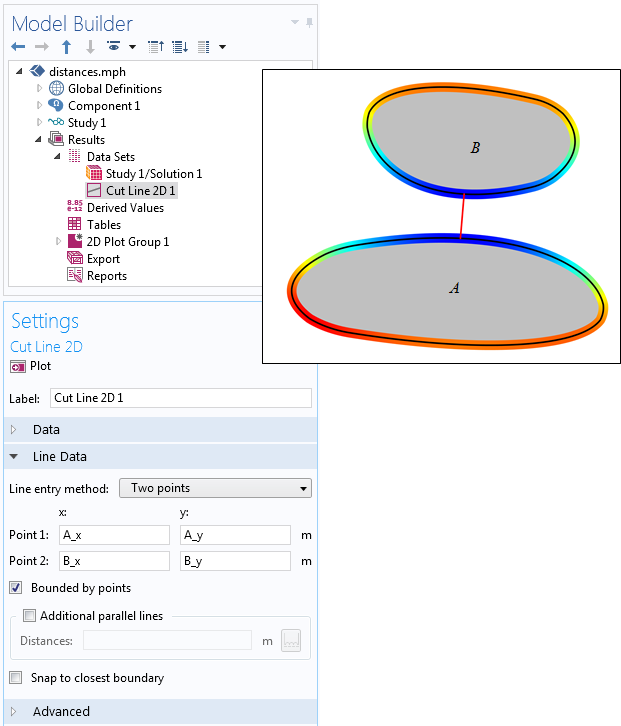
カットライン機能は, オブジェクト間の最短線を決定するために使用されます.
COMSOL Multiphysics® における距離計算の制限と用途
これらの距離決定手法は, どのモデルでも使用できます. ここで示した例は2次元ですが, すべて3次元にも一般化できます. ただし, 3次元距離場の計算には比較的長い時間がかかりますが, 境界とクリアランス間の距離計算はそれほど負荷がかかりません.
滑らかでない形状の周囲の距離場を計算するには, もう少し注意が必要です. 下の図に示すように, 凹角の周囲の距離場は滑らかではないため, 境界の異なる2つの部分から等距離にある線に沿った方向ベクトルは定義されません. この距離場の滑らかさを解決するには, より細かいメッシュが必要です.

凹角を持つオブジェクトの周囲と内部の距離場. 粗いメッシュ (左) とより細かいメッシュ (右). このような場合, 距離場の滑らかさはメッシュに依存します.
適切な細かさのメッシュ上でこの距離場を計算したら, モデル内の他の変数と同様に扱います. 例えば, 材料特性を表面からの距離の関数にすることができます. 下の図は, このような代表的な材料分布を示しています.
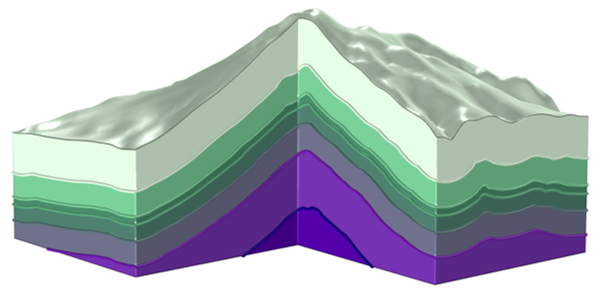
表面からの距離の関数である代表的な材料分布.
距離関数を使用して結果を可視化することも可能です. 表面から特定の距離内にある解の部分のみに関心があるとします. この場合, ボリュームプロットを作成する際に フィルター サブ機能を使用できます. 次に, オブジェクトの表面から特定の距離内にある結果のみを表示する論理式を入力します. その例を以下に示します.
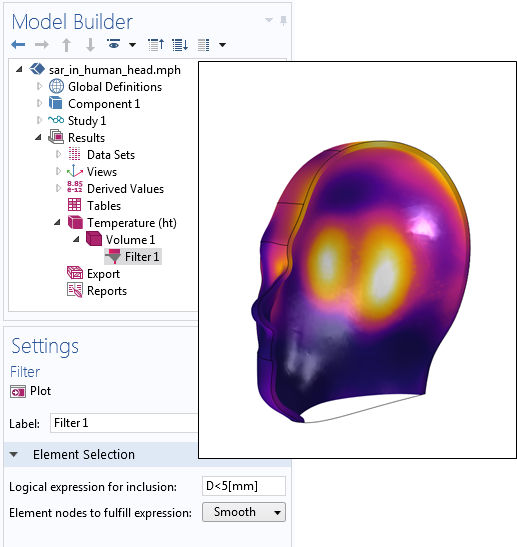
距離関数を使用して, 表面から 5 mm 以内の解のみをプロットします.
COMSOL Multiphysics® におけるオブジェクト間の距離計算に関するまとめ
モデル内の境界までの距離場, 境界間の距離, および2つの境界間の最短線分を計算する方法を説明しました. このアプローチは, 3D モデルのエッジとポイントから距離場を計算する場合にも機能します. 計算された距離は, モデルの設定, 物理特性の定義, 結果評価のどの段階でも使用できます. ここではいくつかの例を紹介しましたが, 次は皆さんの番です. 皆さんの考えをぜひお聞かせください!
その他のリソース
- COMSOL Multiphysics のモデリングに関する様々なヘルプリソースをご覧ください:


コメント (0)