
多くのシミュレーションタスクでは, 計算ドメインの1つの領域 (ソース) から別の領域またはコンポーネント (行先) に変数をマッピングする必要があります. COMSOL Multiphysics では, この機能は, 行先ポイントとソースポイントを関連付ける, 押出し演算子 と呼ばれる点対点マップを定義することによって実現されます. 押出し演算子によってマッピングが確立されると, ソースで定義されたすべての変数に, 同じ演算子を使用して行先からアクセスできます.
領域間の変数のマッピング
1つのコンポーネントまたはコンポーネントの一部から別のコンポーネントまたはコンポーネントの一部に変数をマッピングする必要がある実用的な状況は数多くあります. 1つの例は, 乱流モデルの入口境界条件の生成など, 2つのサブモデルのリンクです. 入口の境界条件は, ドメイン内の流れに大きな影響を与えます. ただし, 入口の流れプロファイルは, 層流の場合ほど簡単には定義できません. 乱流入口境界条件を生成するには, 通常の流入を伴う補助モデルを使用できます. 次に, 出口で得られた速度プロファイルをメインモデルの入口にコピーする必要があります.
2023年3月9日の編集者注: 2つのコンポーネント間のこの手動マッピングは, 完全に発達した流れプロファイルを取得する目的には不要になりました. COMSOL Multiphysics には現在, 完全に発達した流れオプションが含まれており, 層流と乱流の入口境界条件と出口境界条件に適用できます. (詳細については, 5.3a および 5.4 リリースハイライトをご覧ください.)
領域間で変数をマッピングするもう1つの理由は効率性です. 軸対称の熱境界条件と材料特性を持つ 熱膨張 について考えてみましょう. 構造境界条件が軸対称でない場合は, 最初に軸対称の熱解析を実行し, 次に2D軸対称領域から3D領域に温度をマッピングして構造解析を行うことで時間を節約できます.
もう1つの一般的なシナリオは, 境界上の1点の量が別の境界上の1点の量と関連している周期的またはその他の境界条件の実装です. たとえば, ダイオードでは, p-n 接合の片側の通常の電流密度は, 同じ点の電位と接合の反対側の電位に依存します. このようなさまざまな境界条件が COMSOL Multiphysics の適切なフィジックスインターフェースに組み込まれていますが, ユーザーが独自の境界条件を構築する必要がある場合があります.
このようなインスタンスでは, あるドメインまたは境界から別のドメインまたは境界への変数のポイント単位のマッピングが必要です. 今日は, これらのマッピングを構築する方法を示します.
ソースと行先間のマッピング
マッピングの概念には, 2つのジオエントリエンティティが含まれます. つまり, 量がわかっているソースと, その量が使用される行先です. ソースの量 q_s がわかっており, 行先で別の量 q_d を計算したいとします. 新しい量 q_d は, q_s のコピーまたはその関数になります.
この問題は, 次の手順に分解できます:
- ポイント x_d に移動し, q_d を評価します.
- ソースポイント x_s を特定します. これは, x_d に対応します. この座標変換を x_s = T(x_d) で表します.
- q_s = q_s(x_s) を抽出します.
- q_s の値を関数 f:q_s\rightarrow q_d の引数として挿入し, q_d を評価します.
最終的には,
となります.
このブログの焦点は, 変換 T : x_d \rightarrow x_s. です.
COMSOL Multiphysics では, このマッピングを指定するために, 線形押出し 演算子と 一般押出し 演算子. 線形押出し演算子は作成が簡単ですが, その有用性は アフィン変換 に限定されます. 一般的な押出し演算子はより一般的ですが, 定義により多くの作業が必要です.
ここでは, 線形押出し演算子について説明します. 後のブログでは, 一般押出し演算子について説明します.
COMSOL Multiphysics での線形押出し演算子の使用
ソースポイントとターゲットポイントが, 平行移動, スケーリング, 反射, 回転, またはせん断などのアフィン変換によって相互に関連付けられている場合, COMSOL Multiphysics では, 押出し演算子を指定する簡単な方法として, 線形押出し演算子が用意されています. 線形押出し演算子を追加するには, 定義 > コンポーネントカップリング > 線形押出し に移動します.
線形押出し演算子の基本的な考え方は, 2本の線上の対応する点のペアが2つわかっている場合に, 2本の線の間のアフィン変換を定義できるというものです. 同様に, 非共線点のペアが3つと, 非平面点のペア (共線点が2つ以下) が4つあれば, それぞれ2Dドメインと3Dドメインのアフィンマッピングを記述するのに十分です.
これは, 一般的な線形系解析に似ています. 十分な数の基底点/ベクトルの変換がわかっていれば, 線形重ね合わせを使用してすべての点/ベクトルを変換できます. 線形押出し演算子は, 基底とその変換を選択する視覚的な方法と考えてください. その情報から, COMSOL Multiphysics は任意の点/ベクトルに適用する必要があるマッピングを自動的に導出します.
これをいくつかの例で説明します.
例 1
最初の演算子は, 方向を保持したまま, 端点 1 と 4 を持つ線分から端点 4 と 5 を持つ線分にデータをマッピングするために使用されます. 必要なのは, 下の図に示すように, COMSOL Multiphysics にどの点がどこに行くかを示すことだけです.
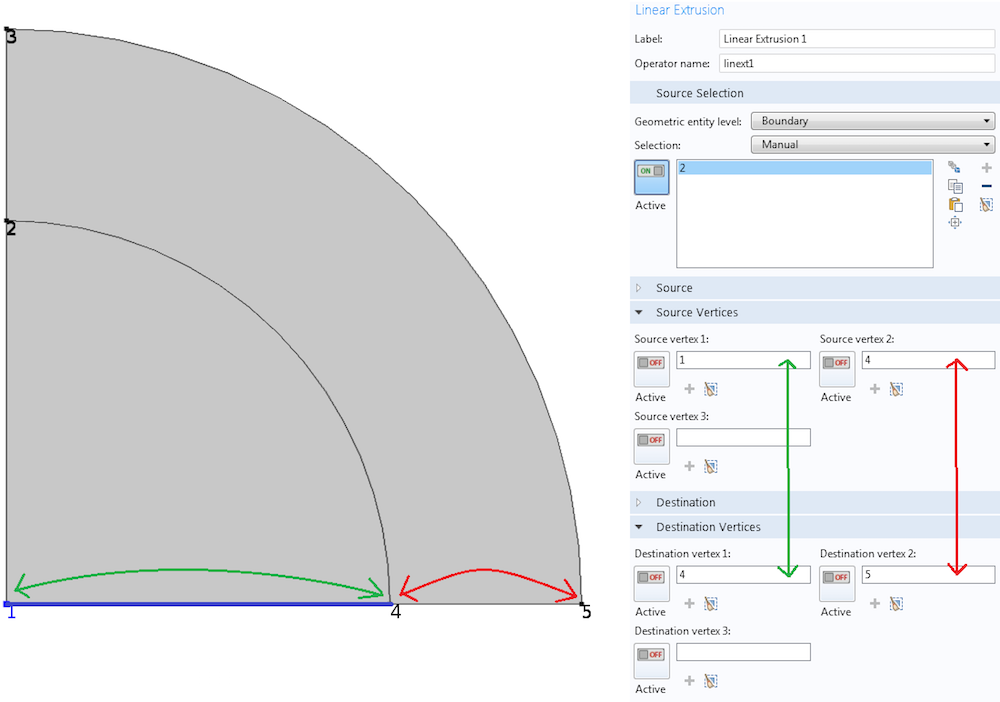
ソースのポイント 1 と 4 を, それぞれ行先のポイント 4 と 5 に一致させる線形押出し演算子.
2D空間にいるにもかかわらず, 1Dオブジェクト (線) を操作していることに注意してください. したがって, 2セットの頂点間の対応を示すだけで十分です. 行先頂点 1 に 5 を選択し, 行先頂点 2 に 4 を選択した場合はどうなりますか. その場合, セグメント 1-4 をセグメント 4-5 に移動するために必要な変換とストレッチに加えて, 反転が行われます. 下のプロットを参照してください.
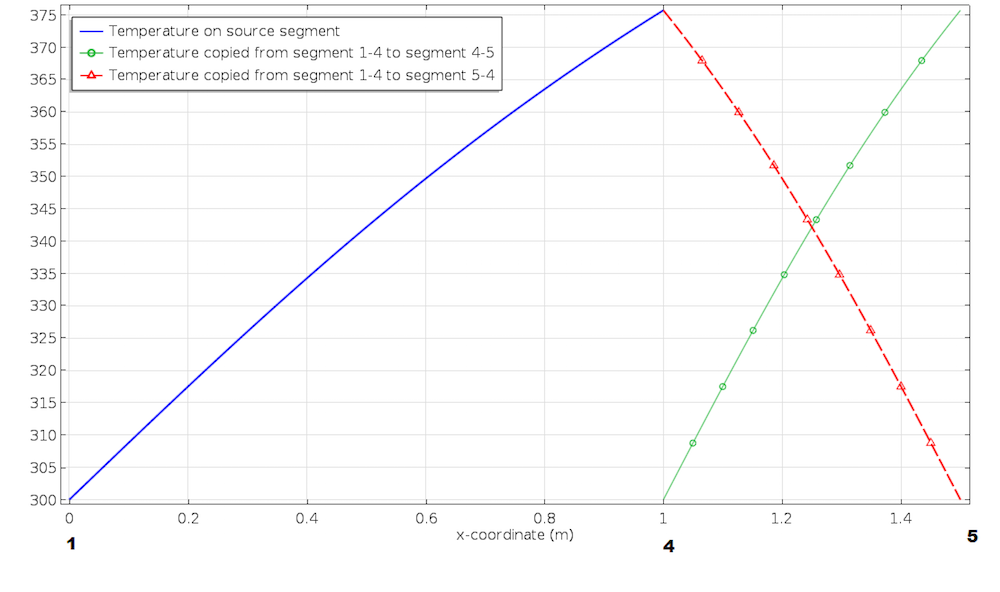
線形押出し演算子のソース頂点とターゲット頂点の下の頂点の順序によって, マッピングの方向が決まります.
例 2
次に, オブジェクトの次元を増やし, 線形押出し演算子を構築して, 放射状に引き伸ばすことで内部の円から外部の領域にデータをコピーします. 必要なのは, 上記の頂点ペアにもう1組の頂点を追加することだけです. 下の線形押出し設定ウィンドウを参照してください.
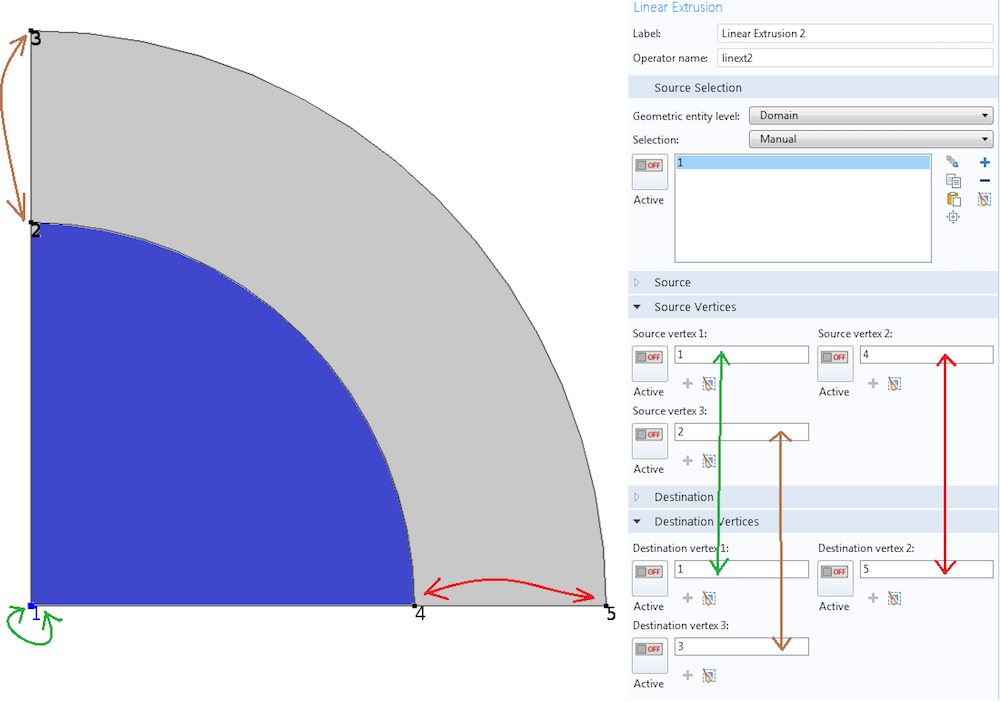
マッピング内のオブジェクトの次元が高いほど, 線形押出し演算子を定義するためにジオメトリ内のより多くの頂点をペアにする必要があります.
マッピングは, ソース ドメインのポイント 1, 4, および 2 を, それぞれ行先ドメインのポイント 1, 5, および 3 に一致させます. これを基底ベクトルの観点から見ると, ソースのセグメント 1-4 は行先のセグメント 1-5 に対応します. 同様に, ソースのセグメント 1-2 は行先のセグメント 1-3 に対応します. これらの2つの線形独立基底から, COMSOL Multiphysics は, 2Dドメインの任意の行先ポイントをソースポイントにマッピングするのに十分な情報を取得します. 下の図は, 内側の円に定義された変数 \phi が, 先ほど定義した線形押出し演算子 linext2 によってどのようにマッピングされるかを示しています.
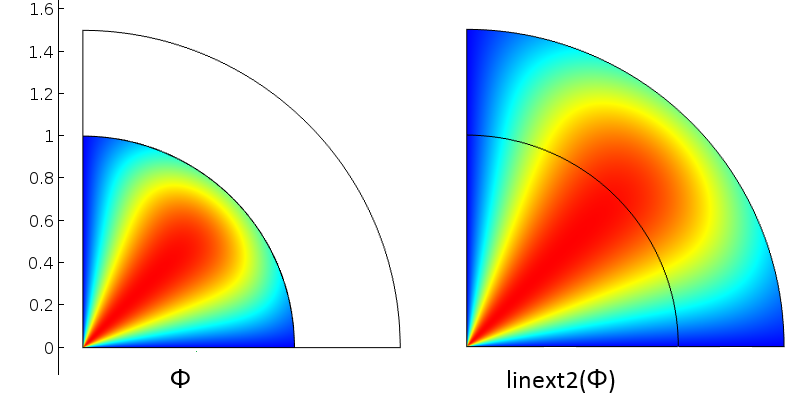
内側の円に定義された変数 (左) が, 線形押出し演算子を使用してすべてのポイントにマッピングされます (右).
量の評価
これまでに行ったことは, 変数にアクセスするためのインフラストラクチャを構築することです. では, 構築したツールの使い方を見てみましょう.
上の画像に示されている線形押出し設定ウィンドウのいずれかを見ると, 上部に 演算子名 が表示されています. この名前は, マッピングにアクセスするために使用します. linext2 が押出し演算子の名前である場合, 目的のポイントで, 対応するソースポイントからの量, たとえば u を参照する場合は, 式 linext2(u) を使用します. 同じソース ポイントから変数 w が必要な場合は, linext2(w) を使用します. これが, これらを演算子と呼ぶ理由です. これらを作成したら, 任意の正当な引数で使用できます.
変数を単に使用する代わりに, 変数の関数が必要な場合は, 関数を演算子内に置くか, 関数を演算子の出力に適用することができます. たとえば, linext2(w^2) は linext2(w)^2 と同等です. linext2(w)+u は linext2(w+u) と同じ値を返しますか? 一般的に, いいえです. 最初のケースでは, 行先ポイントの u が, 対応するソースポイントで評価された w に追加されます. 2番目のケースでは, u と w の両方がソースポイントで評価されます. 以下の画像は, 例 2 の線形押出し演算子を使用してこの点を示しています.
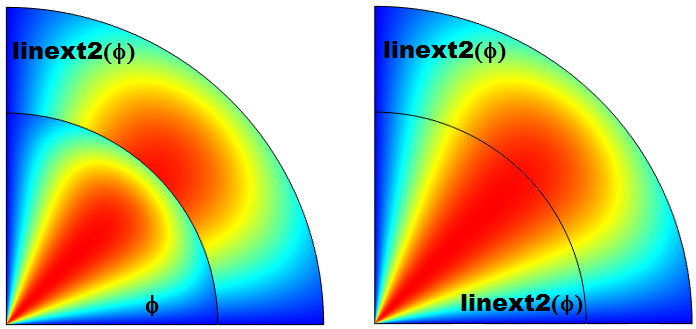
変数 \phi は, 内側の円では行先で, 外側の円弧ではソースで評価されます (左). すべての評価はソースで行われます (右). 一般に, \phi などの引数は, 行先ポイントで有効な量になる可能性があることに注意してください. このような場合, その値は通常, 押出し演算子によって返される値とは異なります.
最後に, 押出し演算子を使用して異なるコンポーネント間で変数をマップする場合, その演算子は, ソースオブジェクトを含むコンポーネントの 定義 ノードに追加する必要があります. 別のコンポーネントで演算子を使用する場合は, そのコンポーネントのタグを使用する必要があります. 線形押出し演算子 linext2 を使用して, コンポーネント 2 から コンポーネント 1 で定義された変数 u にアクセスする場合, 正しい構文は comp1.linext2(comp1.u) です. これにより, 2番目のコンポーネントに押出しや linext2 と呼ばれる別の演算子, または u と呼ばれる別の変数がある場合でも混乱を回避できます.
まとめ
このブログの焦点は, 線形押出し演算子の構築です. 一般押出し演算子の構築方法については, このブログシリーズの パート 2 をご覧ください. ここでは, 完全なモデリング例でその使用法を説明します.





コメント (0)