
空間的に変化するインポートデータを扱う場合, 入力データを正確に求解するためにどのレベルのメッシュ細分化が必要なのか, それがマルチフィジックス問題の解にどのような影響を与えるのかを判断するという課題に直面することがよくあります. このような場合には, アダプティブメッシュ細分化を使用して, モデルの結果に基づいてメッシュを細分化することができます. また, 入力データに基づいてメッシュを細分化するために, アダプティブメッシュ細分化を使用することもできます. 詳しくは, こちらをご覧ください.
不均一な熱負荷のモデリング
この問題では, 外部データファイルから送られてきた空間的に変化する熱負荷で上から加熱された板状の材料が, 区別できる, しかしかなり不均一な構造を持っていると考えます.

外部データファイルから読み込まれた不均一な印加熱負荷を可視化します.
これは COMSOL Multiphysics® ソフトウェアにとっては全く問題ではありません. アダプティブメッシュ細分化を使用すれば, ユーザーが指定した回数だけCOMSOL® ソフトウェアが自動的にメッシュを細分化し, 問題をより正確に求解することができます. このアルゴリズムの数回の繰り返しを以下に示します.
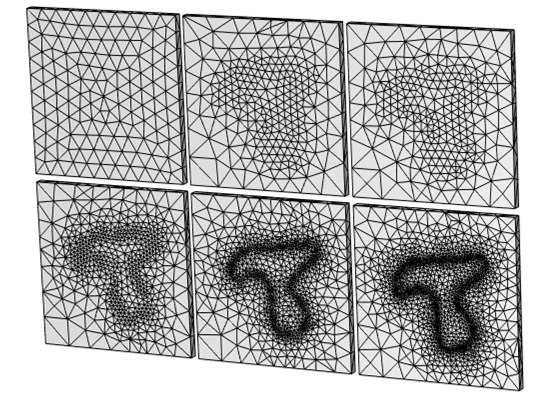
アダプティブメッシュ細分化を使用した場合のメッシュ(上面図)の結果. 一様なメッシュからスタートし, 空間的に変化する熱負荷による解の変化を正確に求解するために, ソフトウェアが要素サイズを調整しています. これにより, 印加された負荷の空間的な変化が再現されますが, この構造が明らかになるまでには, 数回の反復処理が必要です.
これは, アダプティブメッシュ細分化アルゴリズムが, 適用される熱負荷の形状を知らないデフォルトのメッシュから開始されたことを示しています. このアルゴリズムは, 数回の反復処理を経て初めて, 負荷の分布を正確に把握できるようになります.
もっと良い方法があるとしたら?実験データの形状にすでに適応しているメッシュから始めたい, とソフトウェアに伝えることができたらどうでしょうか. もちろん, アダプティブメッシュ細分化を行いたいことに変わりはありませんが, この細分化プロセスを, より合理的な初期メッシュから始めたいのです.
インポートされたデータにヘルムホルツフィルターを適用し, その上でメッシュを適合させることで, これは非常に簡単にできることがわかります. ヘルムホルツフィルターの概念と実装, そしてその利点については, 以前のブログで紹介しました. ここでは, ヘルムホルツが提供する別の機能を見てみましょう.
アダプティブメッシュ細分化とデータフィルタリングの実装
モデルの上面だけにヘルムホルツフィルター方程式を実装し, フィルター半径をかなり小さくして(この半径は入力データの空間分解能に似ていると考えてください), 表面だけのかなり粗いメッシュで解くことができます. ヘルムホルツフィルター方程式自体は線形なので, どのようなメッシュでも解くことができます. また, アダプティブメッシュアルゴリズムは, このメッシュを細かくする必要がある場所を特定することができます. ソルバーとメッシュの設定に少し手を加えるだけでよいのです.
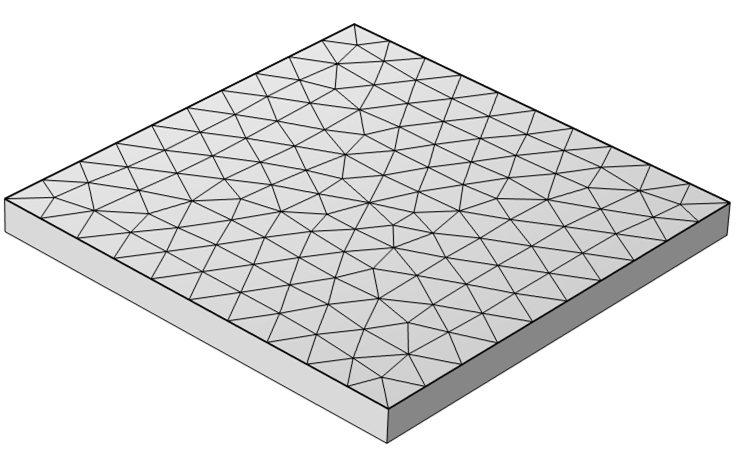
アダプティブメッシュ細分化を開始する際に使用されるメッシュは, 部品の上面のみに適用されます.
ヘルムホルツフィルターを解く定常ステップでは, 1つだけ変更が必要です. 細分化のためのジオメトリエンティティ選択を変更して, フィルターが定義されている領域(ここでは1つの境界のみ)でのみ細分化が行われるようにします. また, オプションで細分化の最大数を増やし, 細分化方法, 特に一般的な修正とメッシュの再構築のオプションを試すことができます.
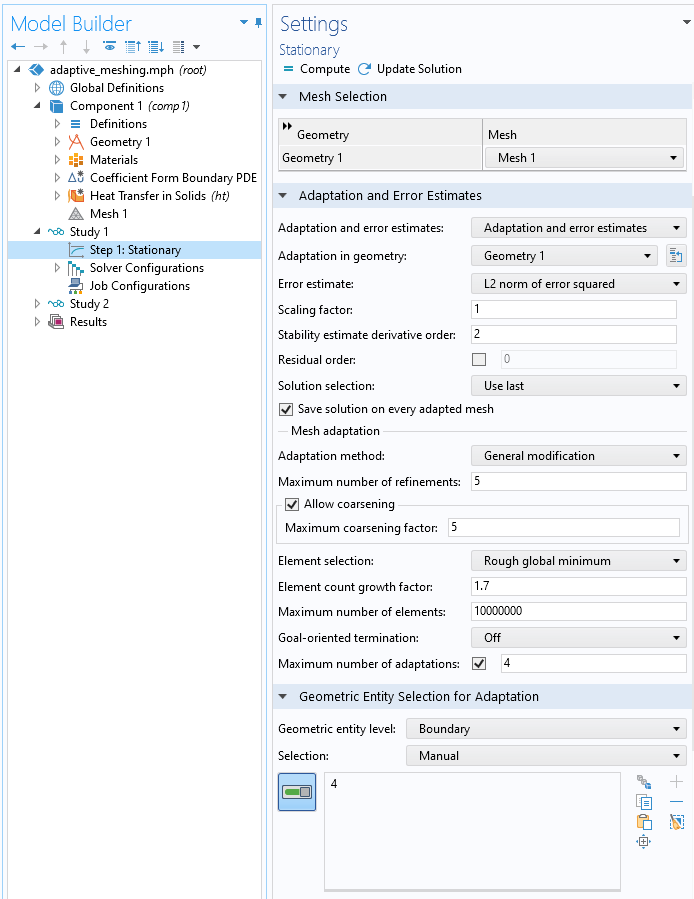
境界線のアダプティブメッシュ細分化を定義する設定.
その他の設定はデフォルトのままで構いません. ソルバーを実行すると, 以下のように, 境界上のフィルター解にのみ基づいて細分化する一連のメッシュが得られます. ソルバーでは, ボリューム内にメッシュがないというメッセージが表示されることがありますが, これは望ましいことです. ここではサーフェス上のメッシュのみを細分化させ, ボリュームのリメッシュはまだ行いません.

アダプティブメッシュ細分化アルゴリズムによって生成された最初の4つのメッシュのシーケンス. これらは上部境界のみに存在.
問題求解のためのアダプティブメッシュの使用
次に, 熱伝導問題を解くための体積メッシュの定義に, アダプティブサーフェスメッシュの一つを使用したいと思います. そのためには, ユーザー定義のメッシュを追加し, メッシュの配列に必ず含まれているグローバルサイズのすぐ後に参照を追加します. その後, フリーの四面体フィーチャーを追加して, 熱伝導問題を解くための完全なメッシュが完成します.
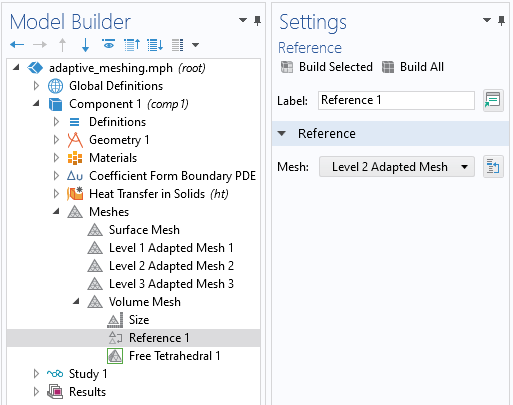
アダプティブに細分化された以前の境界メッシュの1つの結果に基づいて, 新しいボリュームメッシュを構築します.
実際には, このメッシュからさらにメッシュを細分化することも可能です. 利点は, すでに印加される荷重にかなり適応したメッシュからスタートしていることです. したがって, この問題では, 熱伝導解析のために適応的にメッシュを細分化する必要はあまりありません.
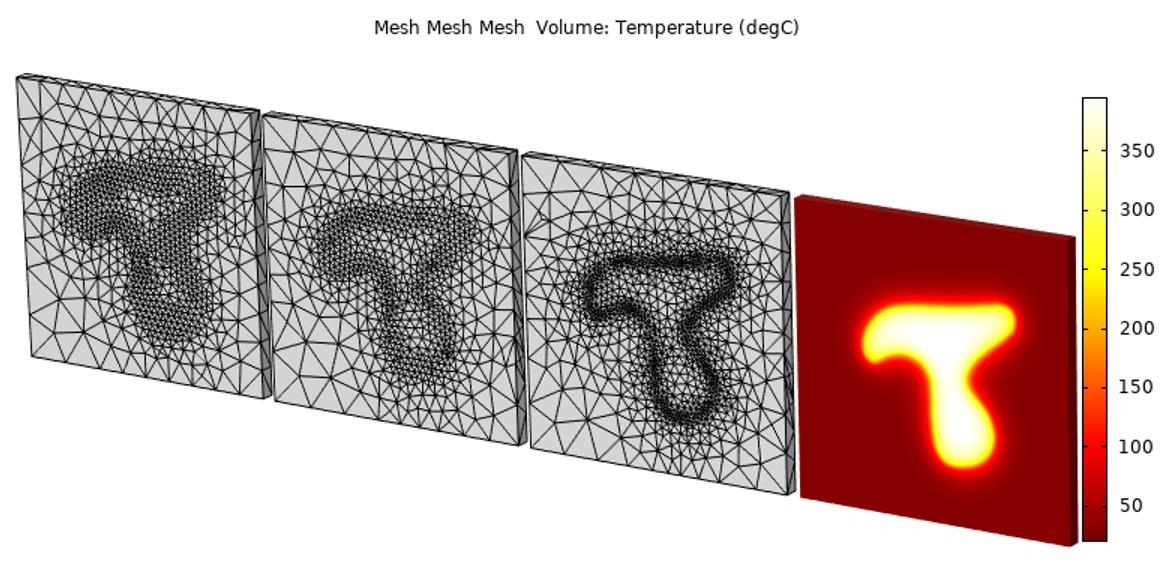
入力データに基づいて改良されたメッシュから始めれば, モデルの解を確信するために何度もメッシュを改良する必要はありません.
このケースでは, 明らかに計算上のメリットがあることがわかります. 空間的に大きく変化する実験データを読み込む場合は, この手法を検討する価値があると思います. 一方で, データが比較的滑らかで, 急激な変化がない場合は, この手法はそれほど強くは求められません.
また, 今回は2次元の平面を対象としていますが, 熱分布を画像ファイルとして扱い画像を曲線の集合に変換する, 任意の2次元作業平面で使用するという方法もあります. ただし, この方法は2Dの平面にしか適用できませんが, ここで紹介する方法は曲面や立体にも適用できます.
お試しください
下のボタンをクリックすると, ここで説明したモデル例に関連するファイルにアクセスできます.


コメント (0)