ステップスラスト軸受は回転機械の軸方向荷重を支えるために使用され, 荷重容量は形状に依存するため, 形状とトポロジの最適化を使用して軸受の荷重容量を最大化することができます. 形状最適化は軸受のステップの形状を変更することで機能しますが, トポロジ最適化は暗黙的な形状記述を使用するため, ステップの数は変化します.
はじめに
ステップスラスト軸受は, 次の仮定でモデル化できます:
- 流体の膜厚は, 横方向の軸受寸法よりもはるかに小さい
- 潤滑剤の薄膜によるせん断効果と比較して, 慣性効果は無視できる
- 物体力は無視できる
- 潤滑剤はニュートン流体である
- 油膜のアスペクト比が大きいため, 面外速度は無視できる
- 速度の大きさは, 面外座標によって解析的に決まる
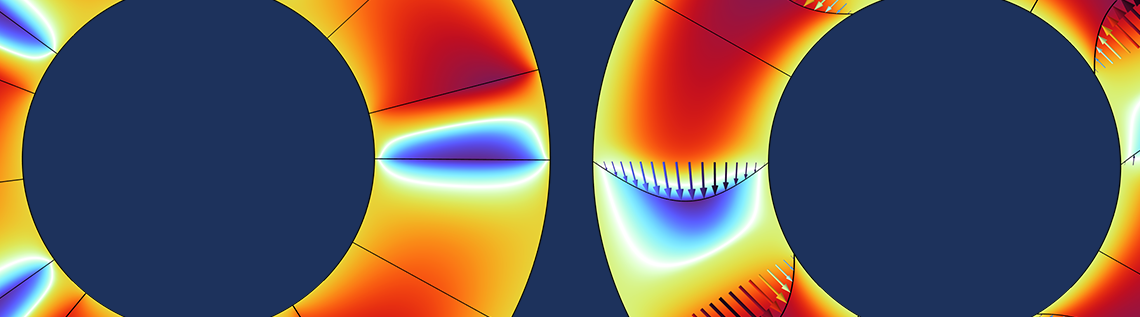
仮定2–4は, ナビエ・ストークス方程式をストークス方程式に簡略化できることを意味し, 仮定5–6は, 流体速度が圧力勾配に比例することをさらに想定することを可能にします. これらの点と他の仮定を考慮すると, 支配方程式は圧力の標準レイノルズ方程式に簡略化されますが, ここではキャビテーションを考慮するために, 代わりにJakobsson–Floberg–Olsson (JFO) 理論が使用されます. これは, 下の図の圧力分布で確認できます. 流体が収縮部を通過すると圧力が低下し, 次の溝の次のステップに近づくまで圧力は増加し始めません.
ステップスラスト軸受はカラー付きで描かれています. 色は圧力を示しています. ステップは明示的な3次元の意味でモデル化されていないため, プロットは計算メッシュを表していないことに注意してください.
軸受の物理特性は, COMSOL Multiphysics® ソフトウェアの流体軸受インターフェースを使用してモデル化されます. この機能では, 面外寸法は明示的に考慮されません. 代わりに, 平面ジオメトリが使用され, 厚さの変化は, 上の画像に示すように, 方程式で直接考慮されます.
荷重容量は圧力分布に依存し, 圧力分布はステップの形状に依存します. したがって, 支持容量を最大化するために形状最適化を適用することは理にかなっています.
ここで, \boldmath{f}_\text{c}はカラーに作用する分布力であり, ポアズイユ, クエット, および法線圧力成分から構成されます. 前述のように, モデルはキャビテーションを考慮していますが, キャビテーションの重大性を制限する試みは行われていません.
形状最適化
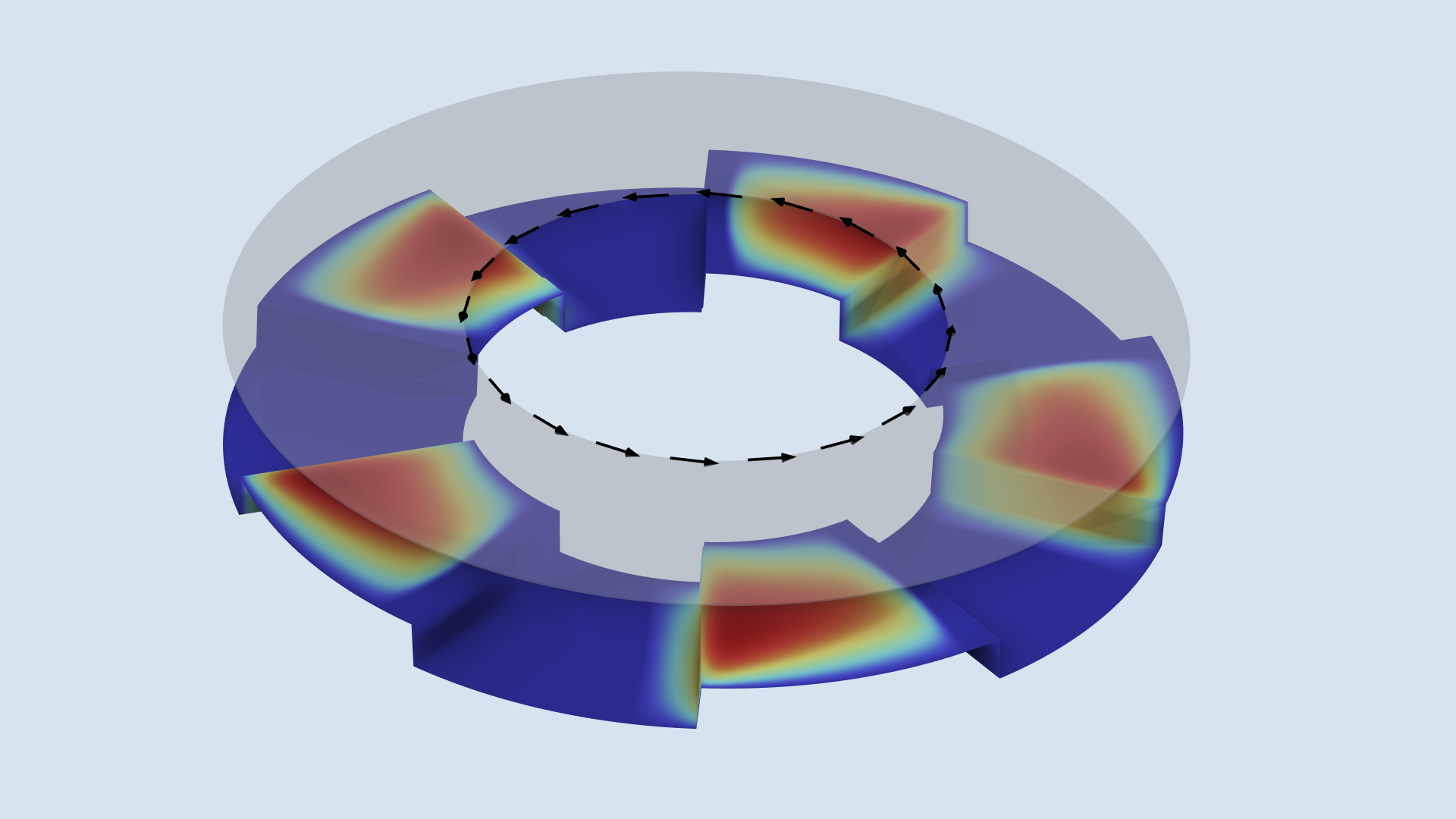
形状の最適化は, メッシュ変形を使用して既存の形状を変更することによって実行されます. 形状の最適化インターフェースには, これを実現するための組み込み関数が多数ありますが, この特定のケースでは, 面外変形が無効になっている3次多項式シェル機能が使用されます. これは, パッドの先端と後端の1セットに使用され, メッシュ変形はセクター対称機能を使用して他のパッドにコピーされます.
ここで紹介したアプローチでは, 円形の境界上の点の位置を固定しますが, これらの点を円形の境界に沿ってスライドさせることもできます. ただし, そのためには方程式ベースのモデリングと, ステップの後縁と前縁に個別の制御関数機能を使用する必要があり, 設定が複雑になります. 設計の自由度が増してもパフォーマンスはわずかに向上するだけなので, このブログではよりシンプルなアプローチに焦点を当てていますが, 代替の定式化は COMSOL® バージョン 6.1 のアプリケーションライブラリに含まれており, アプリケーションギャラリー からダウンロードできます.
形状最適化の結果は, 下の図に示されています. 結果は, エッジの最大変形と初期の溝角度に依存します. 最適化により, オイルがパッドに押し出される前に中央に沿ってオイルを押し込む設計が実現します.
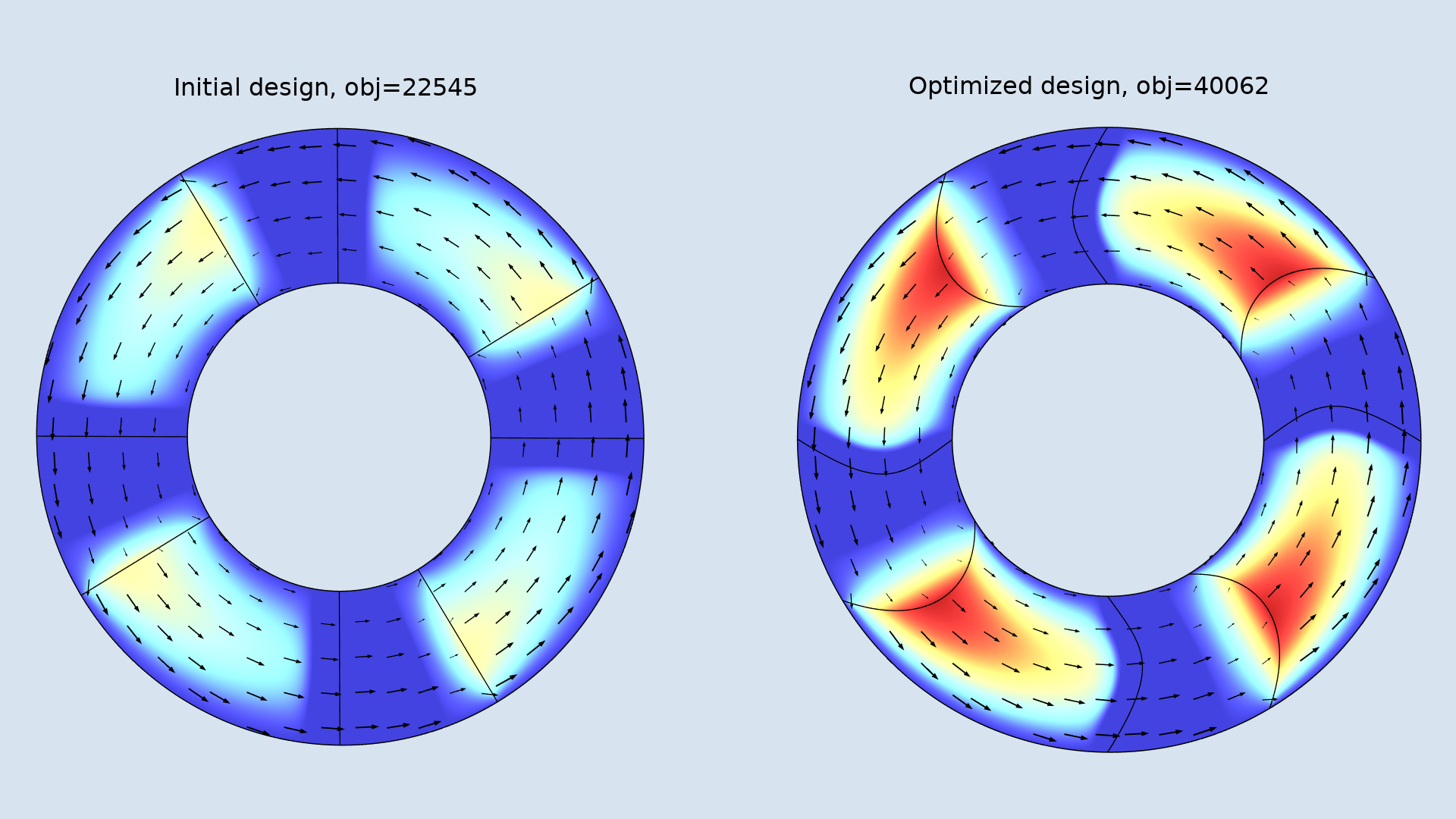
初期設計 (左) と最適化設計 (右) を一緒に示します. 平均流体速度は矢印でプロットされ, 色は圧力分布を示しています.
変形した構成で再メッシュして検証を実行することをお勧めします. このモデルのアプリケーションライブラリバージョンでわかるように, 検証では数値上の問題は見つかりません.
この例では, 最大変形量と溝角度はパッドの数に依存しないように固定されています. このため, 最適なパッドの数は, 以下に示すように4つです.
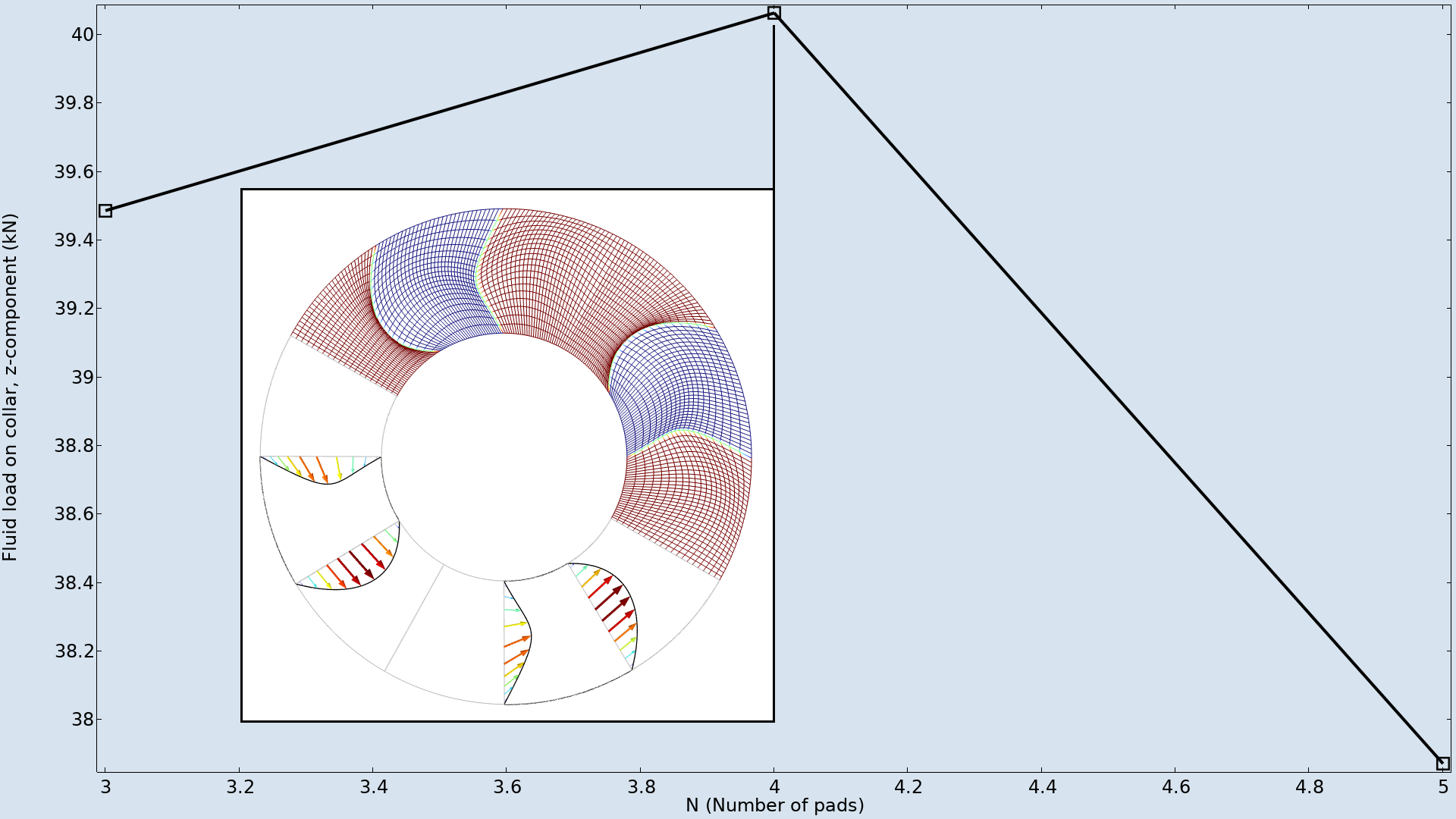
異なる数のパッドに対して形状最適化を実行し, その結果をグラフ化します. 最大値は4つのパッドで発生し, 挿入図はメッシュがどのように変形するかを示しています.
形状最適化は物理特性に関係なく同じように機能するため, 設定が簡単です. 形状最適化によって生じるメッシュの歪みは数値的な問題を回避するために制限されていますが, ユーザーは, 大きな設計自由度と大きなパフォーマンス向上, および小さな設計自由度と堅牢な最適化のバランスを自由に試すことができます. いずれにしても, 最適化された設計は, トポロジ (およびステップ数) が最適化への入力にしかならず, 出力にはならないという意味で, 初期ジオメトリに大きく依存します. トポロジ最適化は, ジオメトリの暗黙的な記述を導入することで, この問題に対処できます. この方法には独自の欠点がありますが, この場合は大きな複雑さなしに使用できます.
トポロジ最適化
トポロジ最適化は, すべての計算要素に設計変数 \theta_c を導入することで機能します. これは0から1の間の閉区間に限定されます. 変数は, 次のように物理特性と関連している必要があります:
- 設計変数が 0 の場合, 溝に対応する支配方程式が解かれます
- 設計変数が 1 の場合, パッドに対応する支配方程式が解かれます
- 設計変数が 0 から 1 の間である場合, 溝とパッドに対応する方程式を組み合わせた支配方程式が解かれます
溝とパッドの唯一の違いは油膜の厚さ h_f であるため, この厚さを設計変数に依存させることで上記の要件を満たすことができます. 他のトポロジ最適化問題では, 3番目のポイントの詳細に特別な注意が必要ですが, この場合は単純な線形補間で十分であることがわかります:
ここで, \theta_f は物理で使用される場であり, \theta_c は制御変数場です. この場合, \theta_c = \theta_f を設定できますが, 制御変数場の小さな長さスケールを除去するフィルターを導入することで収束を改善できます. これにより, 結果の評価と検証のためのよりスムーズな結果も得られます. フィルターは偏微分方程式 (ヘルムホルツフィルター) として表すことができます.
ここで, R_\mathrm{min} は最小の長さスケールです. (トポロジ最適化のためのヘルムホルツフィルターと正規化の詳細については, ブログ “密度法によるトポロジ最適化の実行” を参照してください.)
最適化では, 設計変数を中間値に設定することができます. この場合, これを中間の油膜厚さとして解釈できますが, 中間値には明確な物理的表現がないことがよくあります. 少なくとも, 実用的な関連性のある表現はありません. この問題は, 最適化によって中間設計変数なしで自動的に解が見つかるという意味で, 本質的に適切に設定されているように思われます. つまり, パッドと溝の間に明確な区別があるということです.
トポロジ最適化は, 設計変数の均一な値から始めるのが最適です. これにより, 4つのパッドを備えた設計が実現されますが, 下の図に示すように, 異なる局所最適値を促進するために, 非均一な設計から始めることもできます.
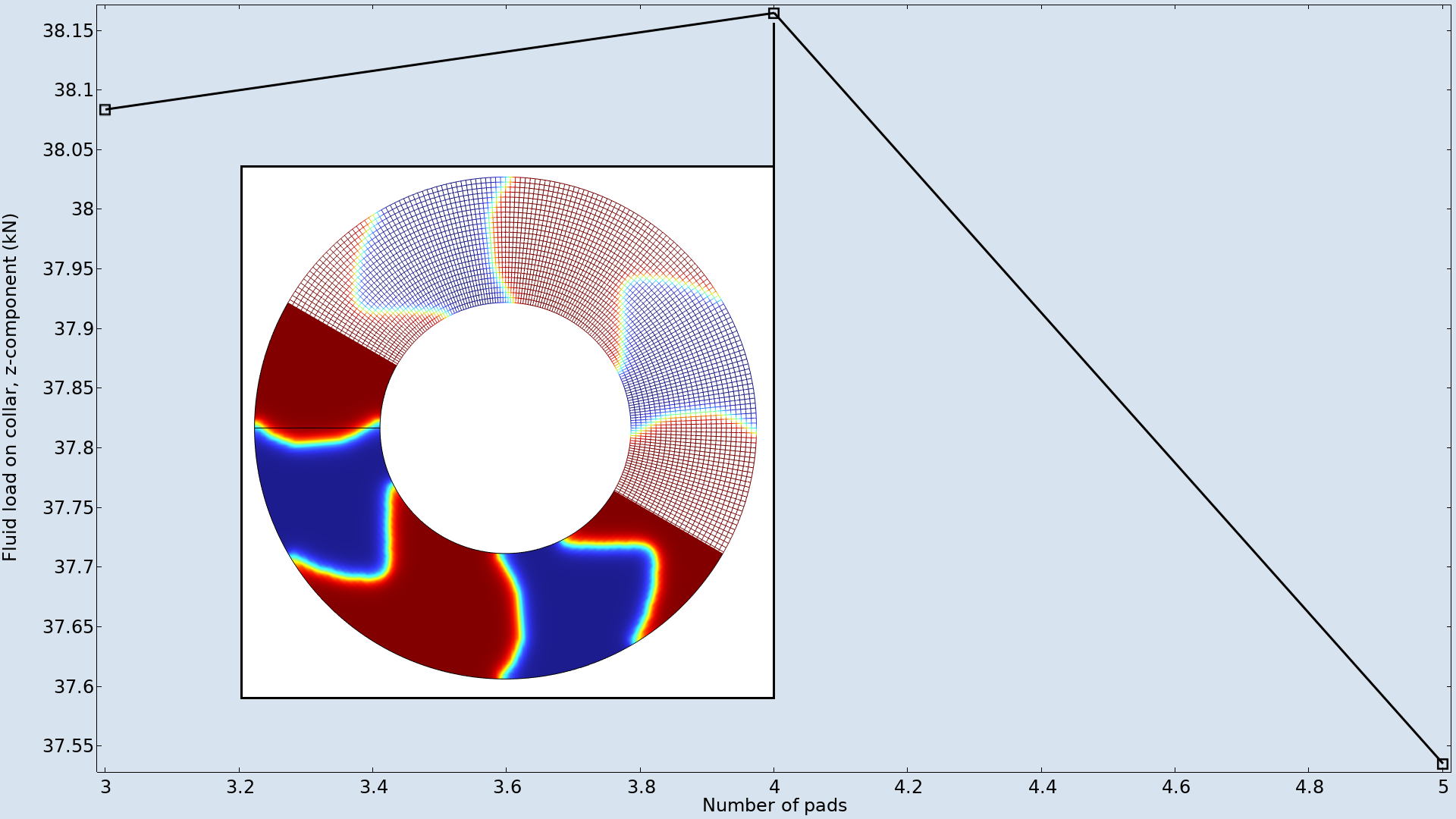
トポロジ最適化は, 特定のトポロジを促進するために, さまざまな非均一な初期設計で初期化されます. グラフは, 最適なパッドの数が4であることを示しています.
これらの設定では, 形状最適化とトポロジ最適化の結果はよく一致しているようです.
トポロジ最適化を実行した後, 検証シミュレーションを実行するのも良い方法ですが, 形状最適化の検証は変形要素に関連する数値の問題をチェックするのに対し, トポロジ最適化の検証は暗黙的なジオメトリ表現に関連する問題をチェックするために使用されます. したがって, トポロジ最適化の検証では明示的なジオメトリ表現が使用され, これにより大幅に優れた目的関数が生成されます. これは, 暗黙的なジオメトリ記述にかなりのコストがかかることを示しています. これをさらに調査すると, 下のアニメーションに示すように, より細かいメッシュを使用すると, トポロジ最適化で大幅に優れた目的を達成できることがわかりました. このアニメーションでは, 16個のパッドを持つトポロジを促進するように設計が初期化されています. 結果として得られる設計は, 以前の設計と質的に似ており, ヘリンボーン溝付きスラスト軸受に似ています.
16個のパッドで初期化された軸受のトポロジ最適化.
すべての最適化では固定の回転方向が考慮されており, これは最適化された設計で明確に確認できます. 初期設計は回転軸に対して対称であるため, この制約を緩和することでパフォーマンスを向上できることは明らかです. このため, 最適化で両方の回転方向が考慮される場合, 目標も小さくなることが予想されます.
結論
ここでは, 形状最適化とトポロジ最適化を使用してステップスラスト軸受を設計する方法について説明しました. ここで説明したフィジックスと最適化の設定は, これらのモデルと関連する解説書で調べることができます:
参考文献
最適化の詳細については, 以下の参考文献をご覧ください:
- ステップスラスト軸受 (およびその他) の最適化を可能にするソフトウェアのアドオンについてお読みください:
- 構造力学のトポロジ最適化について詳しくは, 以下のブログをご覧ください:





コメント (0)