ガウシアンビームは, 光源の中で最も人気のある光源です. このブログでは, 非近軸ガウシアンビームの背景場のエバネッセント成分, 電磁波,波動光学の周波数領域インターフェース, および COMSOL Multiphysics®ソフトウェアのバージョン5.5のRFモジュールで利用可能な機能について説明します.
近軸および非近軸ガウシアンビーム
ガウシアンビームは, 可能な限り最小のスポットに集束する電磁ビームの1つです. 集束角度が小さい場合は近軸ガウシアンビームと呼ばれ, より広角に集束する場合は非近軸ガウシアンビームと呼ばれます.
近軸ガウシアンビームはより長い歴史があり, KogelnikとLiによる近軸理論によって明確に定義されています(近軸理論については参考文献1Ref. 1を, 近軸式については参考文献2Ref. 2を参照してください). 一方, 非近軸ガウシアンビームの理論はそれほど利用されていません(参照3) (Ref. 3).
COMSOLは, バージョン5.3aの時点で, 非近軸ガウシアンビーム背景場を導入しました. この定式化は, 非近軸の場合に近軸ガウシアンビームを使用するよりも優れた近似です. 非近軸ガウシアンビームの定式化は, 次の2つの部分で構成されます.
- 伝播成分
- エバネッセント成分
バージョン5.3aには伝播成分が含まれており, バージョン5.5の時点で, 定式化は本格的になりました. つまり, エバネッセント成分が含まれるようになりました. この成分は, 場のごく微小な部分を計算します. これは高度に非近軸のガウシアンビームにとって重要です.
角度スペクトル定式化
角度スペクトル法に基づく非近軸ガウシアンビームの導出derivation of the nonparaxial Gaussian beamについては, すでに説明しました. 説明は非近軸定式化の一般的な紹介でした. このブログでは, もう少し実用的な定式化について説明します.
伝播方向がz軸である完全なベクトル場を考えてみましょう. 偏光の選択方法に応じて, さまざまな表現があります. 明らかに異なる数学を示す少なくとも3つの参考論文(参照3–5) (Ref. 3–5)がありますが, 本質的なポイントはすべて同じです. このブログでは, 最も単純で理解しやすいChaumetの定式化に従います. 半空間(つまり, z>0)において, 次のようになります.
ここで, k_0^2=(\omega/c)^2 = k_x^2+k_y^2+k_z^2とA_i(k_x,k_y), i=x, yは角度スペクトル関数と呼ばれ, 偏光はE_{x,0}とE_{y,0}で決定されます.
この場が自動的にヘルムホルツ方程式とマクスウェル方程式(ガウスの法則)を満たすことは, 手計算で簡単に確認できます. また, この定式化では, 角度スペクトル関数に任意の積分可能な関数をとることができることも簡単にわかります.
前回の記事で説明したように, この定式化は, 平面波がさまざまな角度で伝播してガウシアンビームを形成する様子を3次元的に表しています. 主な伝搬方向はz軸なので, 平面波の伝搬角度は, 横方向の平面, \vec{k}_0すなわちxy平面\vec{k}_xと\vec{k}_yへの射影によって特徴づけられます(xy平面). すべての平面波の総和は, k_xとk_yに関して積分することを意味します.
ガウシアンビームの場合, 角度スペクトル関数は従来, 焦点面内で選択され, ガウシアンプロファイルであると仮定されています;すなわち.,
この角度スペクトル関数は, 多くの波がz軸であるゼロに近い角度であり, 角度が大きくなるにつれて高角度の寄与が先細りになることを意味しています. ここでは, それぞれのk_xとk_yの積分が,-\infty から+\inftyの範囲にあることに注意してください. 積分の寄与の大部分は, -k_0からk_0の範囲にあることになります. この解を伝搬成分と呼びます. (これはバージョン5.3aで追加されたものです.)
数学的には, マクスウェル方程式はもう一つの解を受け入れます. それは, 積分の寄与がk_0から+\inftyまでの範囲と, 同様に-k_0と-\inftyからの範囲にあることです. この解をエバネッセント成分と呼びます. これは, バージョン5.5から追加された機能です. この場合, 何が起こるかというと, 例えば, k_x=k_0, k_y=k_0の場合, k_z^2 = k_0^2 – k_x^2-k_y^2 = -k_0^2 のようになります. 従って, k_z = ik_0これを上の式に代入すると, ファクター, \exp[-k_0z], が得られます. これは, 場が焦点から遠くに伝搬するにつれて急速に減衰します. z=0 つまり, 伝搬成分に比べればごくわずかな部分です. この成分を取り除いても, 非近軸ガウシアンビームの良い近似となりますが, 集束角が大きくなると無視できなくなります.
COMSOLMultiphysics®での非近軸ガウシアンビームのシミュレーション
フィジックスノードでは, 非近軸ガウシアンビーム背景場を定義するための設定を確認できます. 知っておくべきことがいくつかあります.
完全な横モードは存在しない
まず, 2Dの面外の場合を除いて, 焦点面の近くに非近軸ガウシアンビームの完全な横モードは基本的に存在しないことが知られています. これは, 少しですが常に縦成分が含まれているためです. この事実から, 場の偏光の定義はもはや明確ではありません.
下のスクリーンショットを見てみましょう. これは, 2Dでx軸に沿って伝搬する面内非近軸ガウシアンビームの設定の例です. ガウシアンビームの振幅を(0,1,0)として選択した場合でも, x成分の電場が発生します. 設定に関係なく, COMSOL Multiphysics はマクスウェル方程式を解こうとし, 必要な縦方向成分がある場合はそれを出力します.
エイリアシング
上記の定式化には積分が含まれています. COMSOL Multiphysicsでこれらの数式を実装するには, これらの数学演算をすべてデジタル化して数値的に処理する必要があります. サンプリング数が十分に大きくない場合にアーティファクトが発生するエイリアシングと呼ばれるサンプリングの問題が発生します. 波数ベクトル数と最大横波数の設定は, この問題に関連しています. 自動が機能しない場合は, これら2つの数値を微調整することをお勧めします.
波数ベクトルカウントは, 連続的な無限の数の角度ではなく, 平面波を伝播する離散的な角度の数を定義します. 以下の設定では, 無限に大きい数ではなく, 51の角度が選択されています. これは2Dには十分な大きさですが, 3Dの場合, 合計波数カウントは波数ベクトルカウントの2乗であるため, シミュレーションがフリーズするので注意してください.
最大横波数は, 虚数の縦波数にどれだけ許容できるかを定義します. たとえば,下のスクリーンショットのように, 横波数に2*ewfd.k0を選択すると, k_x^2 = k_0^2- k_y^2 = k_0^2 – 2k_0^2 = -k_0^2が得られます. この場合は2Dなので, 横波数はk_yで, 縦波数はk_xです. この設定は, -k_0 \le k_x \le k_0の範囲の伝搬成分に加えて, k_xを0から\pm ik_0までを許可することを意味します. エバネッセント成分は基本的に小さいです. したがって, 多くの場合, 2*ewfd.k0で十分です.
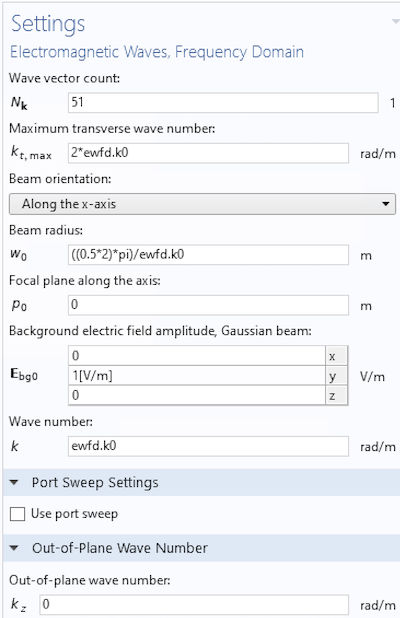
2Dモデルのエバネッセント波設定のスクリーンショット.
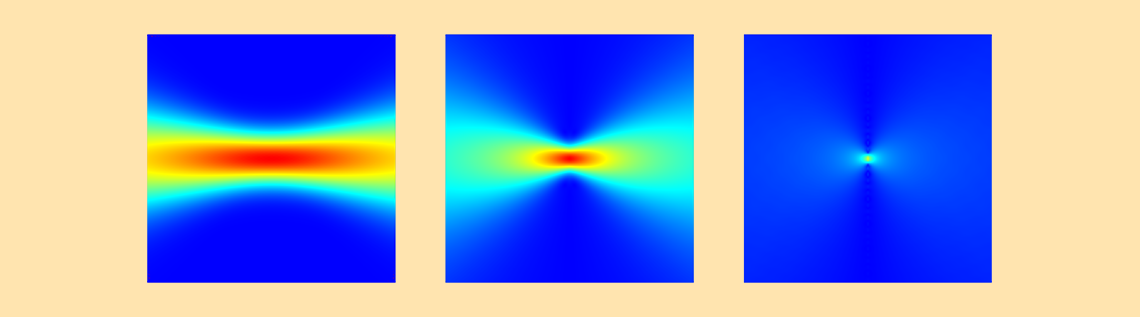
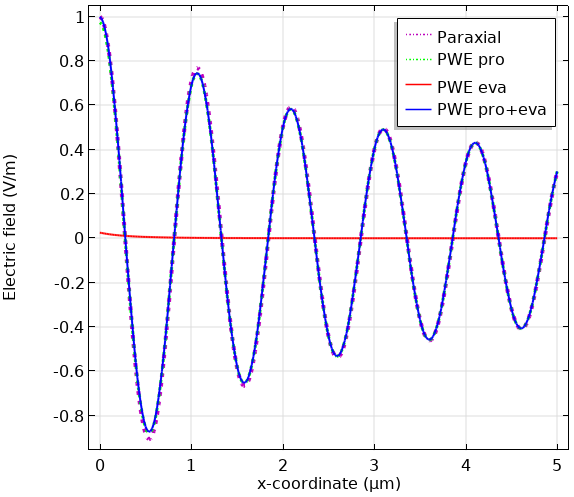
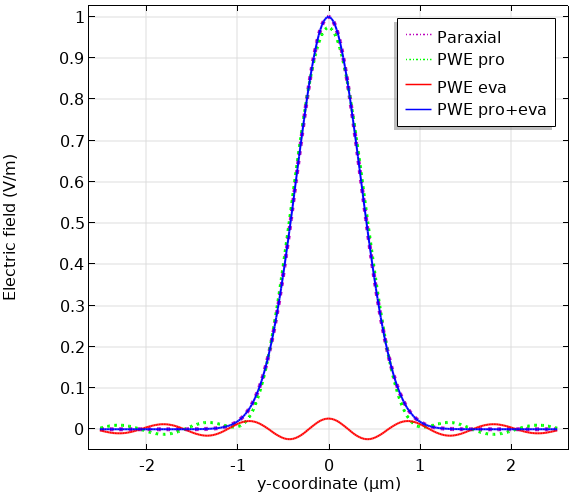
以下は, ウェスト半径が0.5 \lambdaの場合の, 伝播成分を伴う近軸平面波展開(PWE pro), エバネッセント成分を伴う平面波展開(PWE eva), および伝播成分とエバネッセント成分を伴う平面波展開(PWE pro + eva)の比較です. これは非常に非近軸です. 最初の表面プロットは, 場のノルムです. PWEevaおよびPWEpro + evaの場合, 半空間で定義されているため, 正の半空間のみが表示されます. ラインプロットは, 場のxプロファイルとyプロファイルです. これらのプロットは, 近軸ガウシアンビームと非近軸ガウシアンビームの違いが, 焦点面の近くで横方向に発生することを示しています.

近軸近似,平面波展開(伝搬成分), 平面波展開(エバネッセント成分), 平面波展開(伝搬成分とエバネッセント成分)の各方法で計算された電場ノルムの比較.
近軸近似, 平面波展開(伝搬成分), 平面波展開(エバネッセント成分), 平面波展開(伝搬成分とエバネッセント成分)の各方法で計算されたx軸とy軸の電場の比較.
最後の表面プロットは, ヘルムホルツ方程式からの誤差です(誤差の定義については, 前のブログを参照してください). これらのプロットは, ヘルムホルツ方程式に対する解の厳密さの改善をより印象的に表現しています.

近軸近似, 平面波展開(伝搬成分), 平面波展開(エバネッセント成分), および平面波展開(伝搬成分とエバネッセント成分)の各方法で計算されたヘルムホルツ方程式を満たす解からの誤差の大きさの比較.
おわりに
エバネッセント成分を非近軸ガウシアンビーム背景場機能に追加することにより, マックスウェル方程式のすべての可能な厳密解を含む完全な定式化になりました. 上記のプロファイルプロットに見られるように, 近軸ガウシアンビームの式は, 非近軸領域に対して驚くほど正しいように見えます. ただし, エラープロットを見ると, 非近軸の場合の領域でヘルムホルツ方程式を満たさないことが明らかです. これが, 非近軸ガウシアンビームの厳密な定式化が必要な理由です.
参考文献
- H. Kogelnik and T. Li, “Laser beams and resonators”, Applied Optics, vol. 5, no. 10, pp. 1550–1567, 1966.
- “Gaussian beam”, Wikipedia, https://en.wikipedia.org/wiki/Gaussian_beam.
- P.C. Chaumet, “Fully vectorial highly nonparaxial beam close to the waist”, JOSA A, vol. 23, no. 12, pp. 3197–3202, 2006.
- R. Martinez-Herrero, P.M. Mejias, and A. Carnicer, “Evanescent field of vectorial highly non-paraxial beams”, Optics Express, vol. 16, no. 5, pp. 2845–2858, 2008.
- P. Varga and P. Török, “The Gaussian wave solution of Maxwell’s equations and the validity of scalar wave approximation”, Optics Communications, vol. 152, no. 1–3, pp. 108–118, 1998.



コメント (0)