高速フーリエ変換 (FFT) は, 便利で強力な数値手法です. 最新のCOMSOL Multiphysics® ソフトウェアバージョン 6.0 のリリースでは, この手法に関連する新しい機能である空間 FFT 機能が導入されました. このブログでは, この新機能を光学に使用する方法について説明し, アプリケーション例を示します.
用語と定義
まず, 用語と定義を明確にしましょう. FT (フーリエ変換), DFT (離散フーリエ変換), FFT という 3 つの用語を区別する必要があります. 関数 u の FT は次のように定義されます.
ここで, x と \xi は, それぞれ物理空間とフーリエ空間の変数です. 物理空間変数が時間 t である場合, 変数 \xi は周波数と呼ばれます. 光学では, \xi は空間周波数と呼ばれ, 通常は波長と焦点距離でスケールされます (これについては後で説明します). 一方, x は, 対象の光学構造の近傍の位置を記述するために使用される物理空間座標です.
以前のブログ, “COMSOL Multiphysics® でフーリエ変換を実装する方法” および “計算解からフーリエ変換を実装する方法” では, COMSOL® でFTを実行する方法について議論しました. そこではシンプソン則 に基づく直接数値積分によってFTを実行する数値手法を使用することができます. 以降, これを ”数値積分による FT”と呼びます.
DFT は FT の離散バージョンであり, 離散的な点のセットに対して演算を実行します. COMSOL® では, 次のように定義されます.
FFT はDFT を計算するための効率のよいアルゴリズムです .
FT と DFT のこれらの定義は最も一般的な定義ですが, その符号規則は波動定式化に関する COMSOL® の符号規約, \exp(i(\omega t- {\mathbf k}\cdot {\mathbf x})), と一致していないことに注意してください. この標準定義をフラウンホーファーやフレネルの回折式に使用する場合は, 意図的にこの標準定義を注意して使用しています. この不一致は定常解には影響しません.
空間 FFT 機能の使い方
光学系にCOMSOL® の新しい空間FFT機能を使用する方法を示しましょう. FFT機能は, それぞれ手順1と2を使用して設定および実行できます.
- ステップ 1: データセットの準備
- データセットを右クリックして空間 FFT データセットを追加 → 他のデータセット (これがフーリエ空間を定義します)
- 適当なソースデータセットを物理空間として選択(変換元)
- 空間解像度をマニュアルに設定
- サンプリング解像度を適当な数に設定
- 空間レイアウトでゼロパディングを使用を選択し, x パディングを適当な数値に設定
- フーリエ空間変数で周波数を選択
- DCをマスクのチェックを外す
- ステップ 2:
fft()オペレーターを使ってプロット- プロット設定のx軸データの空間周波数スケーリングを調整
矩形関数の例
矩形関数は, 開口を表すため, 光学分野で最も頻繁に使用される関数の 1 つです. 系に開口部がある場合は, 必ず矩形関数の FT が登場します. 矩形関数のフーリエ変換は手で簡単に計算でき, 次のようであることが知られています:
\begin{cases}
0 & |x|>a/2 \\
1 & |x|\le a/2
\end{cases}
ここで \mathcal F は FT 演算子を表し, a は定数, そして {\rm sinc}(x) = \sin x/x は sinc 関数を表します.
COMSOL® の新しい 空間 FFT 機能を使用して, この FT がどのように計算されるかを見てみましょう.
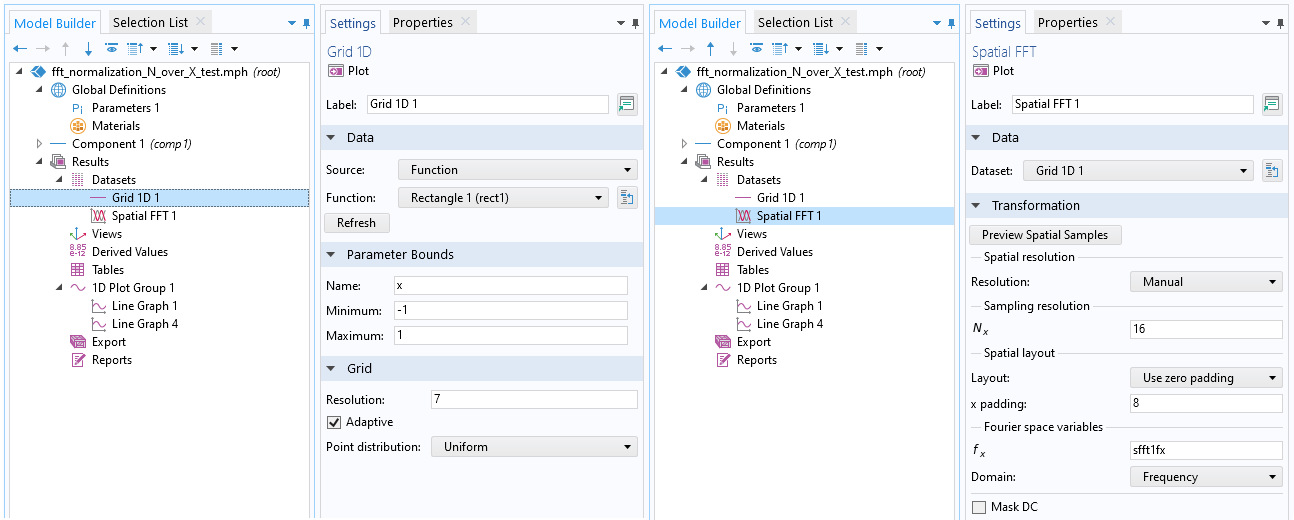
矩形関数 (左) とその FT (右) のデータセット設定の例.
矩形関数は, 定義関数にある組み込み関数です. プロット作成ボタンを押すと, 関数の新しいデータセットが結果のデータセットノードの下に自動的に作成されます. 範囲と解像度もデフォルトで自動的に設定されます. FFT を実行するときは, これらのパラメーターを自分で制御することが重要です. フーリエ空間分解能は, 物理空間範囲の逆数と物理空間データへのゼロパディングによって決まります. フーリエ空間範囲は, 物理空間範囲とフーリエ空間サンプリング数によって決まります. FFT の結果の大きさは, 物理空間の範囲とフーリエ空間のサンプリング数によって異なります. 次の表は, 前の図に示した FFT 設定に対応するパラメーター値を含む, FFT パラメーター式の概要です.
| パラメーター | 式 | 数値例 |
|---|---|---|
| 物体全長 | X_0 |
|
| フーリエ空間サンプリング数 | N_x |
|
| ゼロパディング | N_z |
|
| フーリエ空間全範囲 | N_x/X_0 |
|
| フーリエ空間解像度 | \frac{N_x}{X_0} \cdot \frac{1}{N_x+2N_z} |
|
| FT 正規化乗数 | X_0/N_x |
|
上記の設定により空間 FFT 機能によって計算された矩形関数 rect1(x) とその FT の絶対値 abs(fft(rect1(x)) が次のプロットに示されています. フーリエ空間の全範囲は N_x/X_0 = 16/2 = 8, つまり -4 から 4 です. フーリエ空間のサンプリングポイントの総数が N_x+2N_z = 32 であることが分かります.
何故2N_z なのでしょうか? これは, ゼロパディングでは, N_z 個のゼロが物理空間データの両側に追加されるためです. フーリエ空間分解能は 8/32 = 0.25 です. 正規化を行わないと, FFT 演算の結果は N_x/X_0 倍になります. したがって, ピーク値を1にするには, 結果に X_0/N_x を乗算しておく必要があります. 後で, それぞれ異なる乗算定数を持つさまざまな式に FFT を使用しますので, FFT の結果は1に正規化する必要があります.
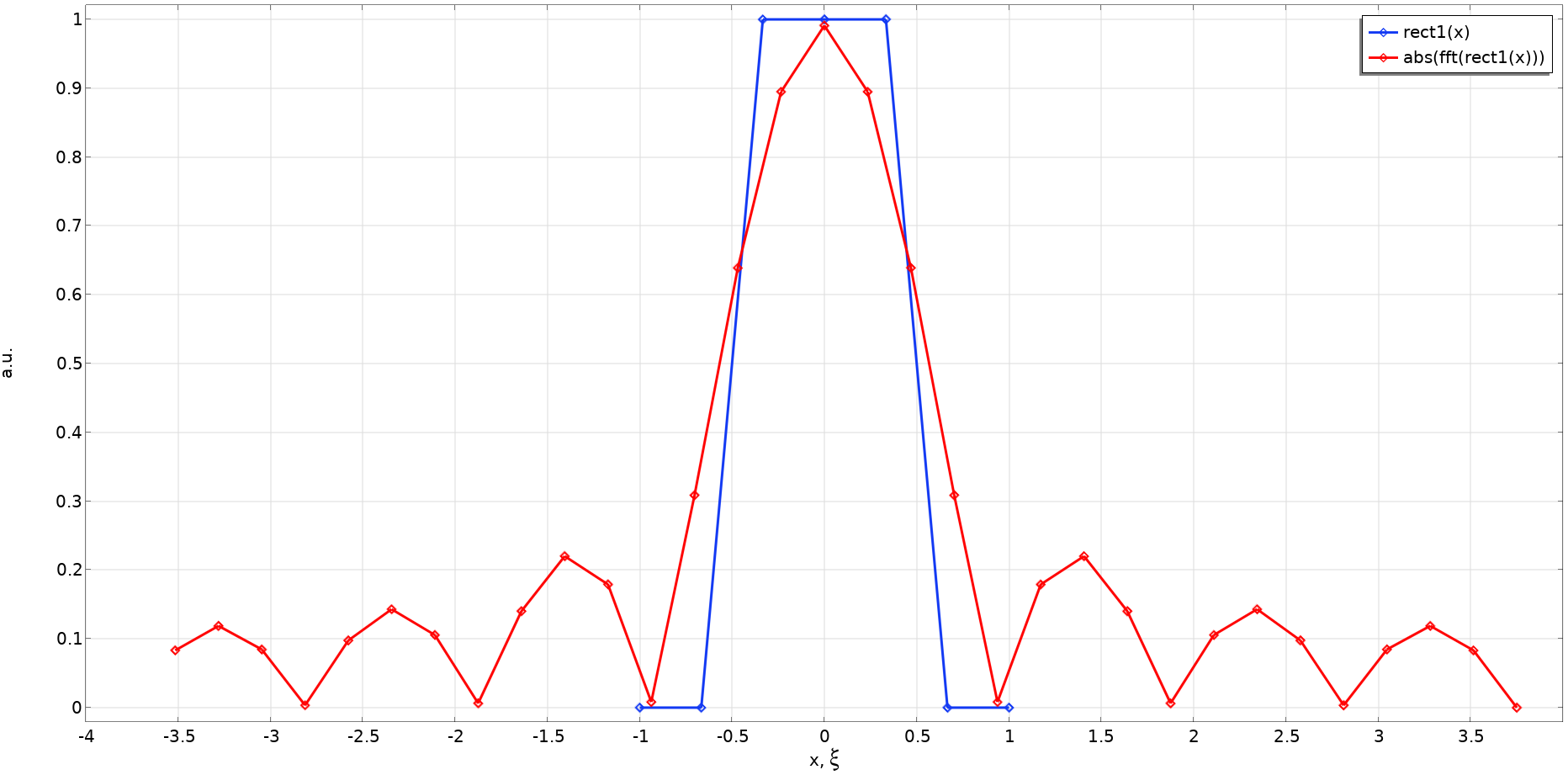
a = 1 の矩形関数と, その FT の絶対値(前に示した設定数値例で決まるFFTで計算).
この例では, 前述の式を確認できるように, サンプリング数が意図的に低い数値に設定されています. それでも, 矩形関数のフーリエ変換の解析式である{\rm sinc}(\pi \xi) が良好な近似値で計算されていることがわかります. より適切なパラメーター (例えばX_0 = 3, N_x = 128, および N_z = 512) を使用すると, 次のような完璧な結果が得られます. 数値積分による FT の結果を重ねて比較します. もちろん, 2 つの方法は一致します!
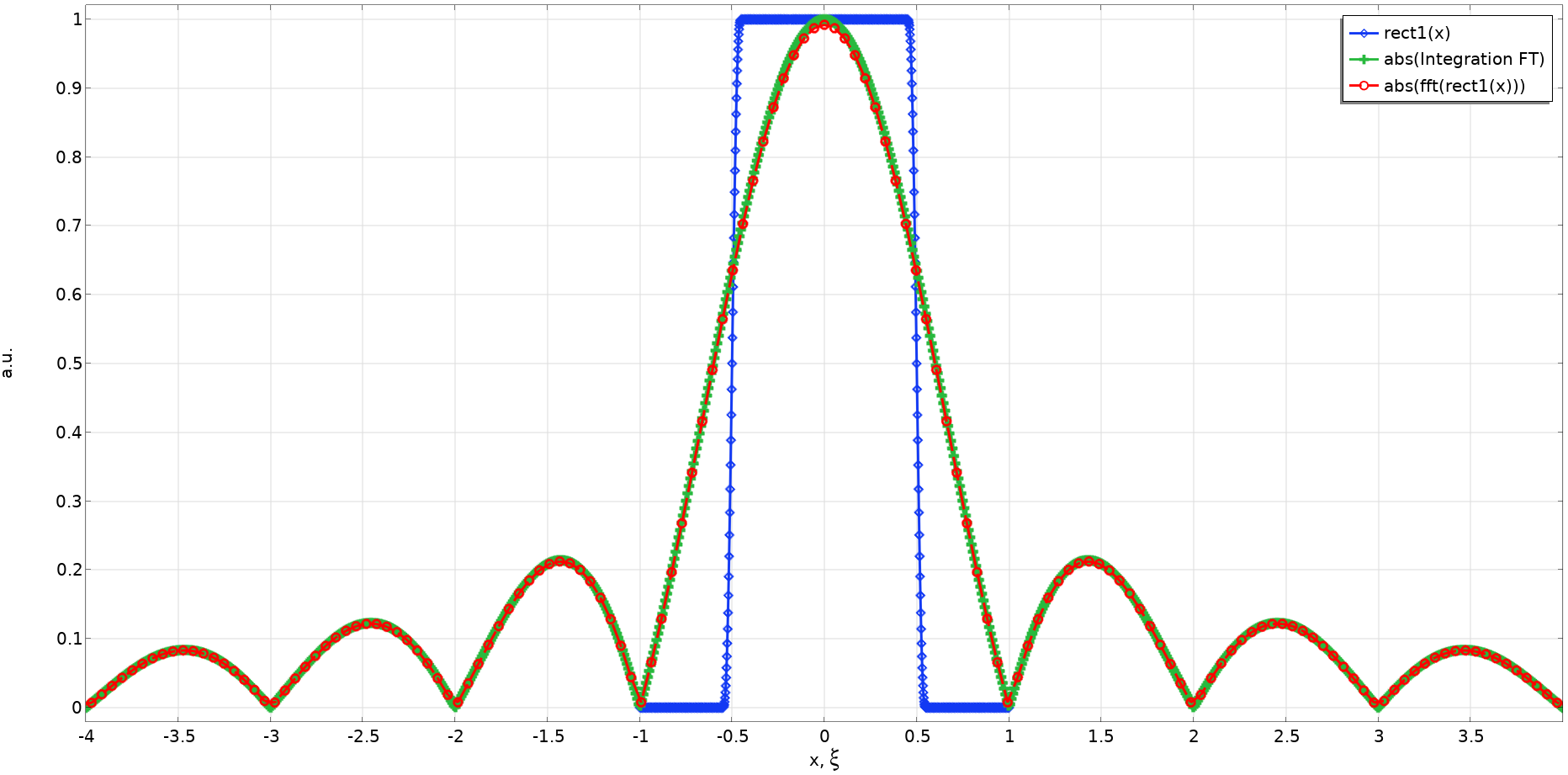
a = 1 の場合の矩形関数の比較. FFT によって決定される, より高い解像度を持つ FT の絶対値と数値積分によるFT との比較.
光学におけるフーリエ変換
これまで, 1D 解析関数である矩形関数の空間 FFT 機能を設定して使用する方法を学習しました. 次に, これを光学分野での実際の応用例に使用してみましょう.
光学では, 光電場の時間信号をそのスペクトル (周波数または波長) に関連付ける時間周波数フーリエ変換の方がよく知られているかもしれません. 空間フーリエ変換は, ある平面から別の平面に伝わる電場のさまざまな伝播 (変換) 計算方法で使用されます. この場合, 空間フーリエ変換は, ある平面内の電場の空間形状を, 他の平面内の形状 (空間周波数と呼ばれます) に関連付けます. 図に示すように, 絞りやレンズなどの平面内の障害物に入射し, 焦点面や像面などの別の平面に到達するスカラー電場またはベクトル電場の成分を考えてみましょう:
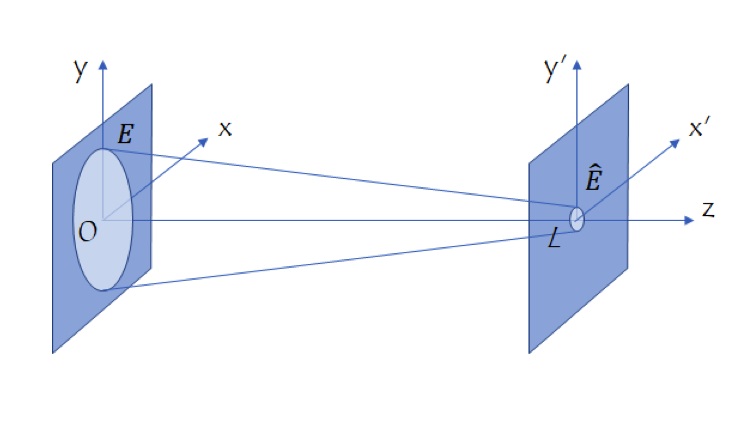
光学における伝播 (変換) 法の座標系.
障害物の後の平面内電場を E(x,y,0) と表します. 別の平面 \hat{E}(x’,y’,L) における電場を計算する方法が, 目的に応じて 4 つあります. 次の表はそれらの 4 つの伝搬方法の公式をまとめたものです. 数式は, 自明な位相関数を省略して, フーリエ変換演算を表す表記 \mathcal{F}[\cdot] によって表されます.
| 理論 | 公式 (簡素化標記) | 応用 |
|---|---|---|
|
1. フラウンホーファー回折理論 |
\hat{E}(x’) = {\mathcal F}[E(x)] |
|
| 2. フレネル回折理論 | \hat{E}(x’) = {\mathcal F}[E(x)\exp(-ikx^2/(2L))] |
|
| 3. 角スペクトル法*** | \hat{E}(x’) = {\mathcal F}^{-1}[{\mathcal F}[E(x)]\exp(ik\sqrt{1-\alpha^2})] |
|
| 4. 部分コヒーレンス理論 (シェルモデル)**** | I_{pc}(x’,L) = {\mathcal F}^{-1}[{\mathcal F}[I_c(x)] {\mathcal F}[\gamma(x)]^\ast ] |
|
注:
* フラウンホーファー回折条件
** フレネル回折条件
*** \alpha は方向余弦
**** I_{pc} は部分コヒーレント強度, I_c はコヒーレント強度, \gamma は相互コヒーレンス関数
フラウンホーファー回折
フラウンホーファー回折式は, フラウンホーファー条件が満たされた場合に物体から回折される遠方場を計算するために使用されます.
次が完全な公式です:
(x’,y’,L) = \frac{e^{i k L}}{i \lambda L} \iint_{-\infty}^{\infty}E(x,y,0) e^{-i 2\pi (x’ x+y’ y) / (\lambda L)}dxdy
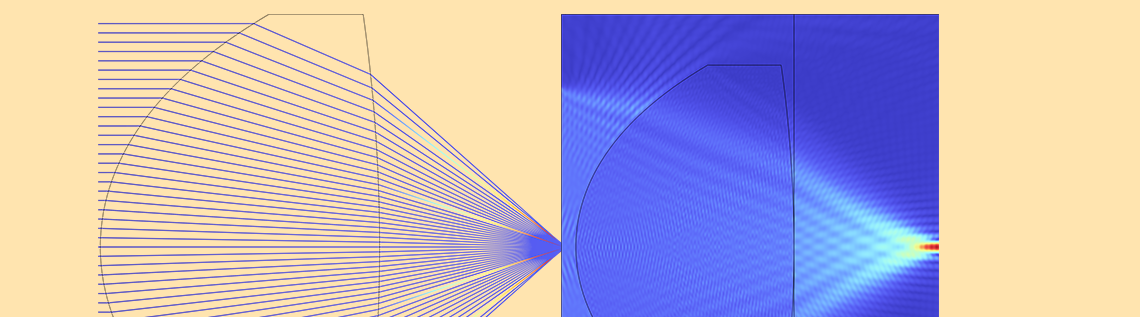
この式は, 開口, 回折格子, およびフーリエ光学の焦点面の遠方場を計算するために使用されます (参考文献 1). オブジェクトは, 均一な照明を備えた正方形の開口部です. 開口部の出射面における電場は 2D 矩形関数であり, 遠方場は FFT によって計算されます. これにより, 回折パターンが形成されます. これは見慣れた光景かもしれません. メッシュカーテンを通して点灯した街路灯を見るときに見ることができます. 空間周波数はf=x’/\lambda L のようにスケーリングされるため, プロット内の x 軸データを \lambda L 倍にスケーリングする必要があることに注意してください. 数値積分による FT を使用した 2D FT の計算には長い時間がかかりますが, FFT は非常に迅速に実行します.
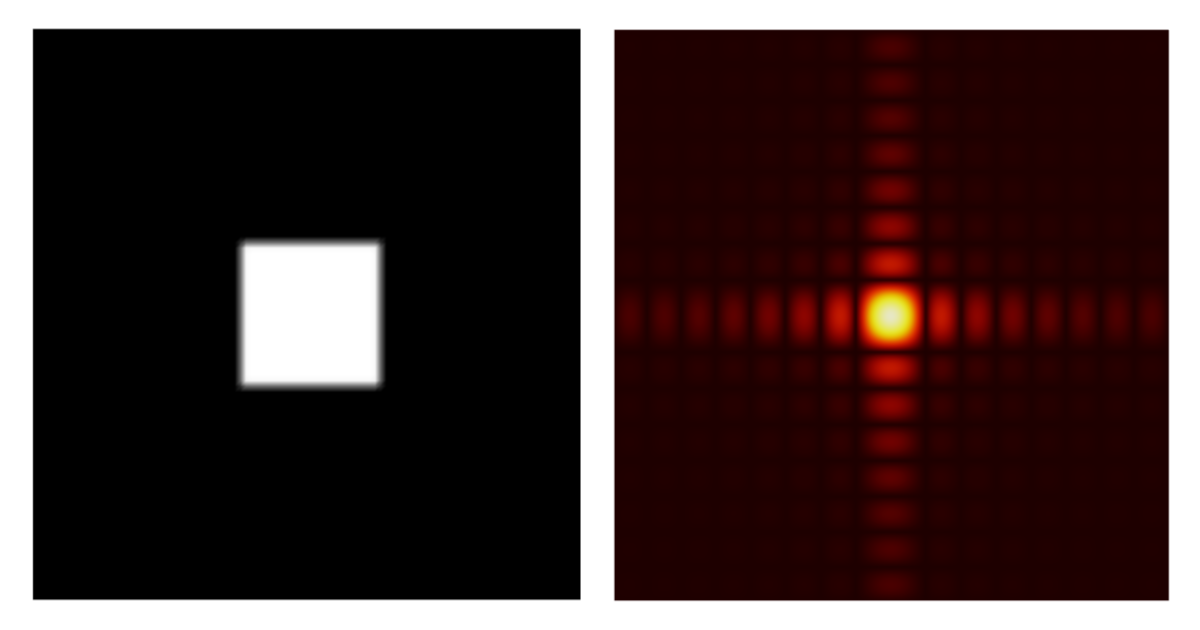
正方形の開口部 (左) とその回折パターン (右).
正方形の開口をシミュレートするための設定は非常に簡単です:
フレネル回折
2 番目のアプリケーションであるフレネル回折公式は, 障害物の近くの場の計算だけでなく遠場の計算にも使用できます. この近似の完全な公式は次のとおりです:
x 軸データは \lambda L の係数でスケーリングする必要があることに注意してください. このアプリケーションは, フレネルレンズモデルで実装されており, そこではレンズ内の電場を求めるために波動光学 (周波数領域)インターフェースが使われています. 次に, 数値積分による FT による焦点面の場を計算するために, フレネル回折公式が使用されました. 以下の図に示すように, FFT 機能をこのモデルで使用すると, 数値積分による FT と同じ結果が得られます.
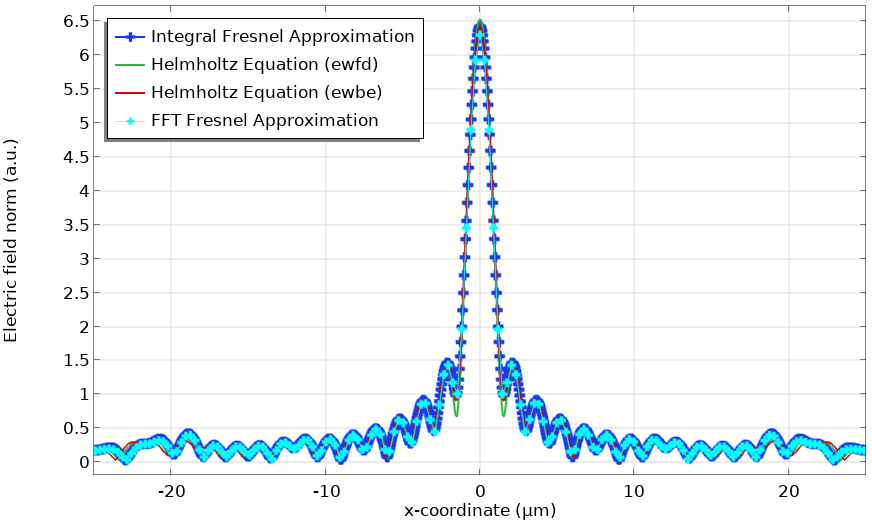
フレネルレンズモデルの焦点面における電場ノルム. FFT 機能はフレネル回折式の計算に使用され, 他の方法と比較されます.
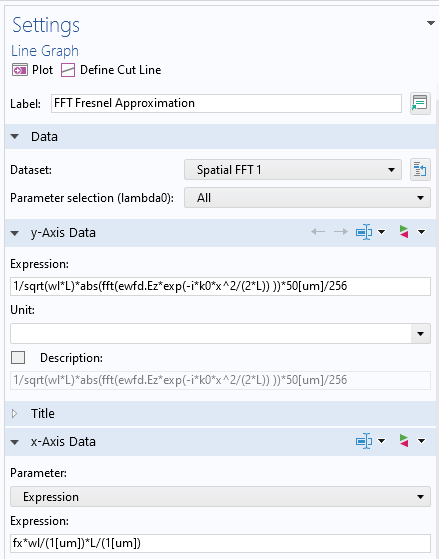
フレネル回折式の FFT 機能のポスト処理設定. y 軸のデータは正規化され, x軸のデータはスケーリングされることに注意してください.
角スペクトル法
3 番目のアプリケーションである角スペクトル法は, 公式からわかるように, FT を 2 回使用する必要があるため, 実装するのが少し難しくなります:
ここで
\alpha および\beta は方向余弦を表します.
前述のブログでは, 大型の光学系をシミュレートする方法を紹介しました. つまり, 波動光学 (周波数領域)インターフェースを使用して, 光学部品の近傍の小さな領域を計算してから, フラウンホーファーまたはフレネル回折式を使うか, ビームエンベロープインターフェースを使用して領域全体をシミュレートするかのどちらかです. ただし, これら 2 つの方法は低 NA レンズにのみ適用可能です. 高 NA レンズには多くのメッシュ要素が必要であり, フラウンホーファーとフレネルの公式では適切な近似を行うことができません. 波数ベクトルが急峻すぎるため, ビームエンベロープインターフェースでも計算領域のメッシュ化に膨大なメモリが必要になります.
大型の高 NA レンズをシミュレートする唯一の方法は, 角スペクトル法(ASM)を使用することです. この方法はフラウンホーファーやフレネル回折式と同種の数値法に属する伝播法です. ある平面の場がわかれば, 別の平面の場を計算することができます. ASM はヘルムホルツ方程式を満たすため, 厳密です. この方法を波動光学モジュールと組み合わせて特定の領域の場を計算し, ASM を使用して場をさらに遠い平面に伝播させることができます.
以下は, DVD ピックアップレンズよりもはるかに高 NA のレンズ (NA = 0.66) の例です. レンズの半径は16 um, 後焦点距離(レンズの第2面と焦点面との間の距離)は10 umです. レンズは, 最適化モジュールと組み合わせた幾何光学インターフェースを使用して, 0.66 um の波長に対して回折限界が得られるように最適化されています. レンズは波動光学 (周波数領域)インターフェースが比較のために厳密な解を計算できるように, 意図的に小さく設計されています. ASM を使用して, このレンズの出射面から焦点面まで場を伝播させる方法を示します.
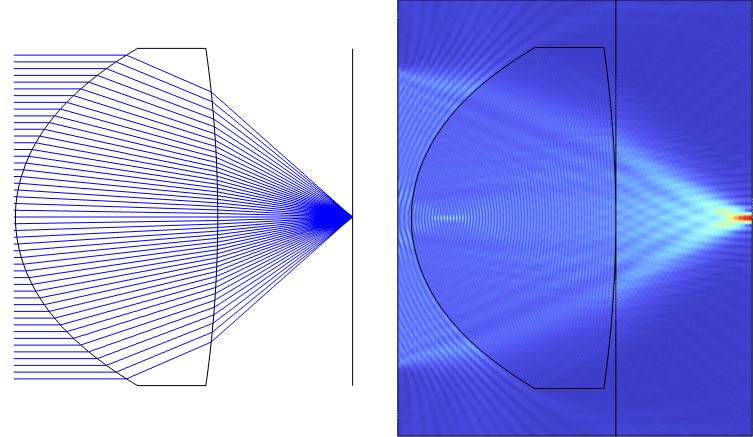 光線光学モジュールと最適化モジュールを使用して設計された NA = 0.66 のレンズ (左). 波動光学の周波数領域インターフェースを使用してシミュレートされたレンズの完全波動シミュレーション(右). レンズの出口面を表す線に注目してください. そこから場が右端, つまり焦点面に伝播されます.
光線光学モジュールと最適化モジュールを使用して設計された NA = 0.66 のレンズ (左). 波動光学の周波数領域インターフェースを使用してシミュレートされたレンズの完全波動シミュレーション(右). レンズの出口面を表す線に注目してください. そこから場が右端, つまり焦点面に伝播されます.
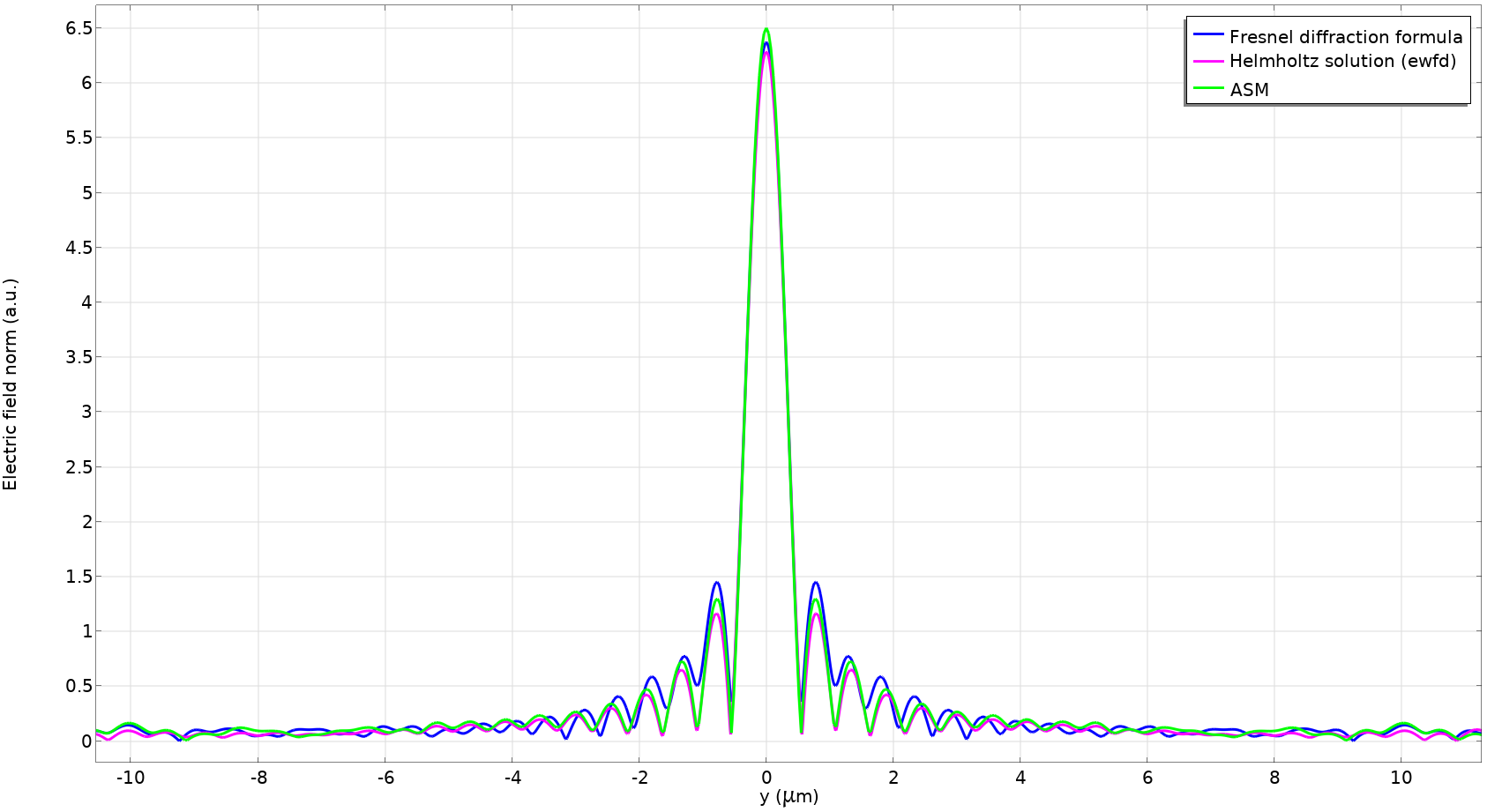
フレネル回折公式を比較した NA = 0.66 レンズモデルのスポットプロファイル. 波動光学 (周波数領域)インターフェースによる厳密解とASM による結果. フレネル回折公式はこのレンズでは正確ではないことに注意してください. (比較しやすいように, スポットプロファイルは焦点面の 10 umではなく 11 um の場所のものを表示しています. )
FT を 2 回実行するには, 最初の FT をデータセットに保存する必要があります. これは, fft() 演算子は単なるポスト処理演算子であり, フィジックス設定で使用できる integrate 演算子のような一般的な演算子ではないためです. 今のところ, COMSOL Multiphysics® の現在のバージョンでは (fft() 演算子が将来のバージョンで一般演算子に昇格するまで), フィジックス設定で数値積分による FT を使用する必要があります. 最初の FT には fft() 演算子を使用し, ポスト処理の 2 番目の FT には fft() 演算子を使用します. 分布 ODE ノードとの境界 ODE および DAE インターフェースはレンズ射出面で定義され, 数値積分による FT を使用して最初の FT が実行され, その結果が得られます. 次の図に示すように, 関数 u として保存されます:
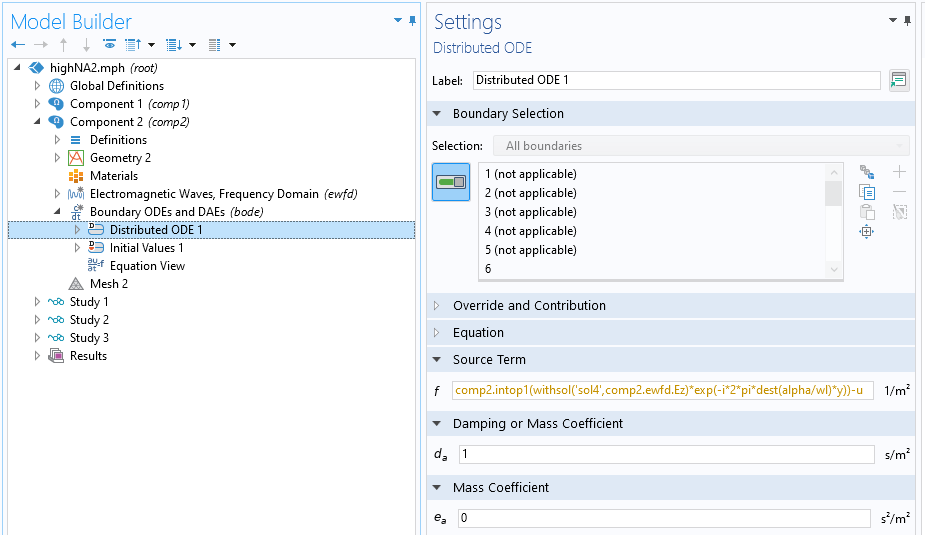 ASM の最初の FT の境界 ODE および DAE の設定のスクリーンショット. 適切なスケーリングのために, フーリエ空間をレンズ半径 D/2 で正規化していることに注意してください.
ASM の最初の FT の境界 ODE および DAE の設定のスクリーンショット. 適切なスケーリングのために, フーリエ空間をレンズ半径 D/2 で正規化していることに注意してください.
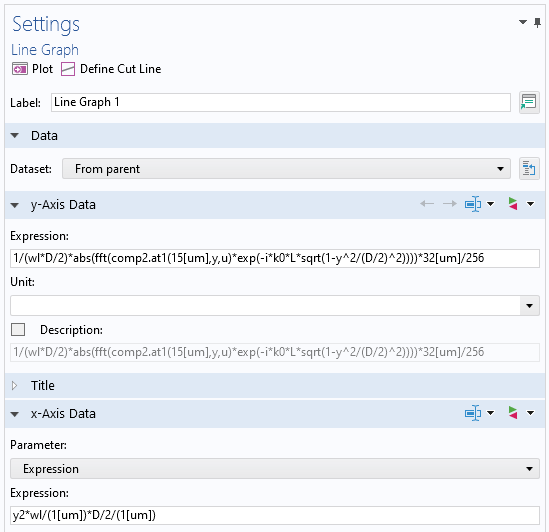
ポスト処理における ASM の 2 番目の FT の設定のスクリーンショット. 方向余弦 a は, 正規化された y 座標によって y 軸データで表されることに注意してください. また, x軸データの規格化乗数 1/wl は2 番目の FT の変数 d(\alpha/\lambda) の全微分から来ます. また, 空間周波数名 y2 は空間FFT のデータセットで任意に選択されることにも注意してください.
2 番目の FT は実際には逆 FT ですが, 定数の範囲で FT の絶対値と逆 FT の間に違いがないことに注意してください. ASM がヘルムホルツ方程式の解として正確な結果をもたらしたことを確認したので, この技術を他の高 NA レンズ系 (たとえば, 大型の高 NA フレネル レンズ) に使用することができます.
終わりに
新しい空間 FFT 機能の設定方法の基本と, 光学分野の重要なアプリケーションでの使用方法の例を見てきました. このシリーズの次回のブログでは, 4 番目のアプリケーションである部分コヒーレントビームの計算 (式はここで 3 番目のアプリケーションで使用したものと同じです) について説明します.
参考文献
- J. W. Goodman, Introduction to Fourier Optics, 3rd ed., Roberts and Company Publishers, 2005.
- M. Born and E. Wolf, Principles of Optics, 7th ed., McGraw Hill, 1968.
- A. C. Schell, “A technique for the determination of the radiation pattern of a partially coherent aperture,” IEEE Trans. Antennas Propag., vol. 15, no. 1, pp. 187–188, 1967.






コメント (0)