
流体の流れを扱うエンジニアの間では, CFDにおける有限要素法の適性について, 常に議論が行われてきました. エンジニアの中には, 有限要素法に比べて有限体積法の方が優れているという確固たる意見を持っている人もいます. この意見には科学的な裏付けがあるのでしょうか?いいえ, 一般的にはありません. 異なる問題には異なる手法が適しているかもしれません. その理由を見てみましょう.
科学, 技術, そして伝統
有限要素法は, 流体の流れに関する数値解析手法を研究するために, 数値解析コミュニティで広く使用されています. CFDや有限要素法に関する科学的な出版物には, 膨大な量の研究成果が記載されており, 最近では, 不連続基底関数を持つ有限要素法であるノーダル不連続ガラーキン(DG)法に関する研究も行われています.
CFD用の商用パッケージは, 伝統的に有限体積法をベースにしています. これは, CFD用の大規模な商用パッケージは基本的にすべて同じ原型を持っているという事実によるものです. これらの手法には, 業界内で膨大な作業と技術が投入されています. 構造化されたメッシュ(例えば六面体, つまりレンガ)と非構造化されたメッシュ(例えば四面体)の両方について, 効率的かつ正確にフラックスを計算し, 統合できるように, さまざまな手法が実装されています.
とはいえ, 流体の流れにおいて, 有限体積法が有限要素法より優れているという仮説には, 理論的にも実践的にも裏付けがありません. 第一に, 有限体積法と有限要素法には様々な種類があり, その中には重複する手法もあります. 第二に, 手法の実装はソフトウェアの実用性に非常に大きな影響を与えます. ある問題群に対して, パッケージXはパッケージYよりも良い仕事をしているようだと言うことができます. しかし, これは一方がFEMを使い, 他方がFVMを使っているからではありません. これについては, 以下でご説明しましょう:
有限要素法か有限体積法. 何がベストか?
数学的モデルと数値モデル
まず, 一般的な数理モデルを紹介します.
(1)
(2)
u = f{\text{ initial condition}} \hfill \\
Bu = g{\text{ boundary condition}} \hfill \\
\end{gathered} $
ここで, P は微分演算子, u は従属変数(解の変数), F はソース, f は初期条件を表す関数, B は演算子, そして g は境界の関数を表しています. 空間座標 \mathbf{x} は, この場合, 3つの方向 (x, y, and z)すべてを表しています.
数理モデルは, 流体の流れなどの物理現象を記述するものであると仮定しましょう. その場合, モデルは空間と時間における運動量と質量の保存を表すものです. 幸いなことに, このような保存法則に由来し, 初期値と適切な境界条件で補完された数学モデルは, 多くの場合, 単純なものです. つまり, 唯一の解が存在し,その解が問題のデータ(例えば, 初期値, ソース項, 境界条件など)に対して連続的に振る舞うということです.
ある問題に唯一の安定した解がある場合でも,その解を解析的に求めることは難しいか, ほとんど不可能なことがあります. つまり, 簡単に計算できる演算(+,-,×,÷)では, 解の解析式を見つけるのが難しい場合があるということです. その代わりに, 数学モデルを近似した 数値モデルを定式化する必要があります. 数値モデルの方程式は, コンピュータープログラムに実装された数値手法を用いて解くことができます.
有限要素法や有限体積法は,モデル方程式の空間の離散化に基づいた数値計算方法です. 時間の離散化は, 通常, 常微分方程式の時間ステップ法の一種で行われます. 上で定義した数学モデルは, 次のような数値モデルを出します.
(3)
(4)
{u_h} = {f_h}{\text{ initial condition}} \hfill \\
{B_h}{u_h} = {g_h}{\text{ boundary condition}} \hfill \\
\end{gathered} $
ここでh は, 例えば, 有限要素法や有限体積法におけるメッシュ要素やセルサイズなどの離散化パラメータを表します.
なお,メッシュの構成要素は, 有限要素法では要素,有限体積法ではセルと呼ばれています.
誤差の原因はいくつかあります. 切り捨て誤差$\tau $は, 数値モデルがどの程度数学モデルを近似しているかを示します.
(5)
数値モデルの精度の次数は, hの減少に伴う切断誤差の減少速度を示しています. つまり, 要素やセルサイズが小さければ小さいほど, 数値モデルと数学モデルの差は小さくなるはずです. 数値モデルは,切り捨て誤差がhに応じて減少する場合, コンシステントであると言われます.
解の離散化誤差は, モデル方程式の厳密解と数値解の差として与えられます.
(6)
hの減少に伴い, 数値解が厳密解に近づけば, 数値手法は収束します.
(7)
離散化の精度の次数pは, hが小さくなるにつれて, 数値解がどれだけ早く正確な解に収束するかを示しています.
(8)
pが大きいほど, 近似値の収束が早くなります.
では, 有限要素法と有限体積法の精度の次数には,本質的な違いがあるのでしょうか? 基底関数の次数を増やすことで, 理論的には有限要素法の精度はどのような次数でも実現できます(実際には別の制限がかかります). 最も一般的な有限要素法は2次から3次の精度で, 有限体積法は1次から2次の精度です.
どこが似ていて, どこが違うのか?
ここでは, 流体の流れの数理モデルの基本となるフラックスバランス方程式を見てみましょう.
(9)
\frac{\partial u}{\partial t} + \nabla \cdot \Gamma = F{\text{ in }}\Omega
この式において, uは運動量や質量などの保存された物理量を表し, \Gamma はその物理量の流束(例えば, 単位面積, 単位時間あたりに制御面を流れる運動量)を表します.
有限要素法は,方程式をテスト関数\varphiで重み付けし, モデル領域で積分することで平均化する積分方程式の定式化から始まります.
(10)
しかし, その前に, 発散定理を\[{\Gamma \varphi }\]に適用してみましょう. これにより, 次のような式が得られます.
(11)
ここで, \partial \Omegaはドメイン\Omegaの境界を示し, \mathbf{n}ドメイン境界への法線ベクトルを示しています. 上の式の左辺を部分積分すると, 次のようになります.
(12)
つまり, 式11から 次のようになります.
(13)
次のような式が得られます.
(14)
式10の第2項に上記の式14を使うことができます. これは, 積分方程式に流束の境界条件を自然に含めるために行われます. さらに, 後の数値計算の際には, 磁束ベクトルを微分する必要がないという利点もあります. その結果, 有限要素法の出発点となる方程式が得られます.
(15)
これは, いわゆる弱形式です. 左辺の第3項は, uのフラックス\Gammaを,ドメインの境界\partial \Omega上で積分します.
弱形式は, 広範囲のテスト関数\varphiで成立する場合にのみ,物理モデルと関係します. 多項式を使うのが一般的ですが, 他の種類の関数を使うこともできます. 特殊なケースとしては, テスト関数が一定の場合があります. 例えば, \varphi = 1という場合です. とすると, 上の最後の式(式15)は次のようになります.
(16)
この関係は, 有限体積法の出発点として使用されます.
ここまでは有限要素法と有限体積法に違いはありません. 以下のように, 有限体積法の定式化である式16は, 有限要素法で用いられる一般的な弱形式である式15の特殊なケースに過ぎません.
この違いは, 式15と 式16の離散化にあります. 有限要素法は, 有限個のテスト関数\varphi = \varphi_hを選び, それらのすべてについて式15が成立するように設定することで得られます. 有限体積法は, 有限個の制御体積\Omega = \Omega_hを選び, そのすべてについて式16が成立するように設定することで得られます. これらの方法の基礎として三角形を使用する場合, 図1と図2はそれぞれ有限要素法と有限体積法の離散化された形を示しています.
最も一般的な有限要素法を見てみると, テスト関数は, いわゆる節点の近傍(ローカルサポート関数)でのみ非ゼロとなります. つまり, 積分はこの近傍の要素(ここでは三角形)に対してのみ計算すればよいことになります. 例えば,図1のハイライトされたドメインノードとその周辺のグレーの要素を見てください. 式15の左辺の第3項である境界流束からの寄与は,境界に面(3D)またはエッジ(2D)を持つ要素についてのみ含める必要があります. なぜなら, 要素間の境界寄与は連続的な基底関数で相殺されるからです. 下の図1は, ドメイン内の内部要素(白, 灰色, 緑)と, 境界上に面(3D)またはエッジ(2D)を持つ要素(水色)に対して, どのように式を立てるかを示しています. 図1 のドメイン内のハイライトされたノードでは, 周囲のグレーの要素のみが( \Omegaに対する)ドメイン積分に寄与しています. 境界でハイライトされたノードでは, 隣接する2つの水色の要素のみが\partial \Omegaに対する積分に境界流束の寄与を与え, これら2つの水色の要素と薄緑色の要素の両方が( \Omegaに対する)ドメイン積分に寄与しています.
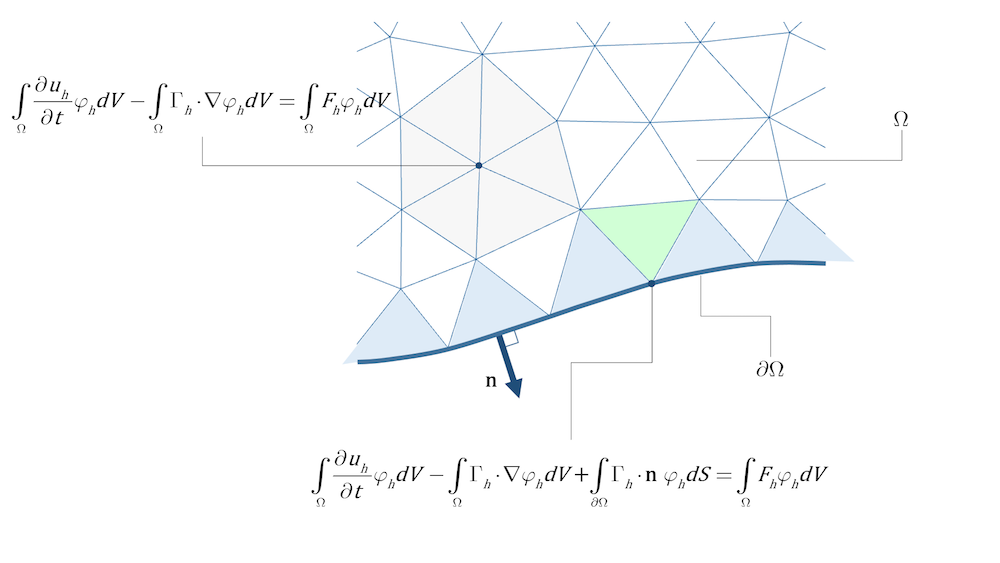
図1. 内部要素(白と灰色)と, 境界に面(3D)またはエッジ(2D)を持つ要素の領域寄与率. 灰色の六角形の中央にあるノードの基底関数は,周囲のすべての要素,すなわち,すべての灰色の要素でサポートされています. 境界にあるノードの基底関数は,水色の要素だけでなく,境界にノードを持つすべての要素(たとえば,薄緑色の要素)でサポートされています. 流束の積分は,境界にエッジを持つ要素(水色の要素)からのみ寄与を受けています.
離散化された流束の領域式\Gamma_hは, 流束の構成関係, 例えば, 対流拡散方程式(流体の流れの方程式における拡散項は, 運動量輸送のための粘性項である)から得られます. 式15の流束の境界式は, 特定のモデルの境界条件から得られます. これらの式は, 上述の図1の境界要素(水色)の寄与度として含まれています.
比較して, 一般的な有限体積法であるセル中心法では, 各セル(三角形)を個別の領域として扱います. 流束の境界項(式16の左辺の第2項)は, すべてのセル(内部のセルと, 境界に面(3D)またはエッジ(2D)を持つセル)について積分されます. ドメインの面またはエッジでは流束の構成関係が使用され, 境界上の面またはエッジでは境界条件が使用されます(下図2参照).
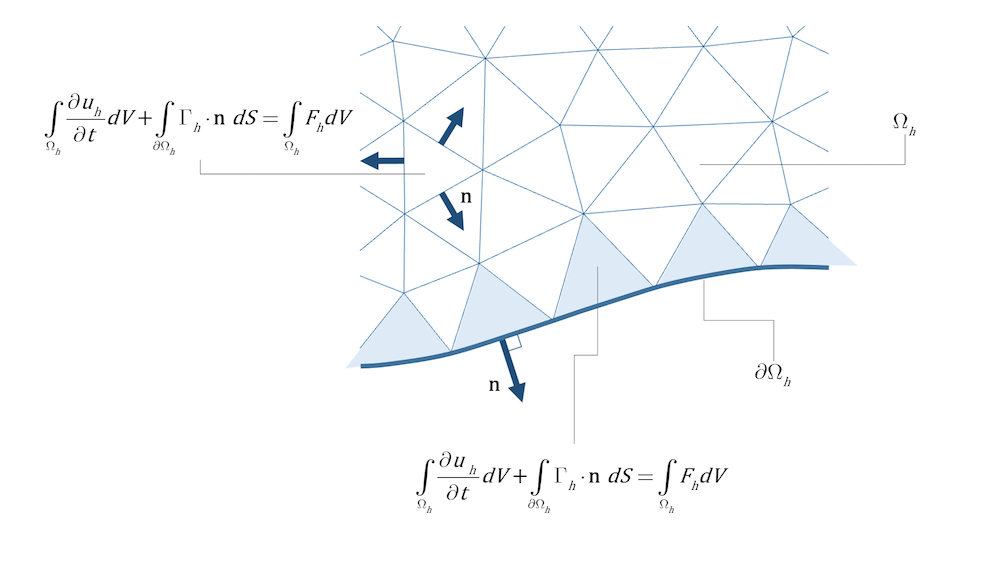
図2. 流束は,内部のセルと,境界上に面やエッジを持つセルの両方について,すべてのセルの面(3D)またはエッジ(2D)にわたって積分されます.
では, 2つの異なる方法でuと\Gammaを表現するにはどうすればよいのでしょう
か.
有限要素法では, 多くの場合, テスト関数と同じ基底関数を用いて解を近似します. 解の近似がゼロよりも高い多項式次数を持ち, 一階の微分が近似できる限り, 対流や拡散で与えられる流束を扱うのに特別な方法は必要ありません. 磁束のベクトルも局所多項式関数となります.
一方, 有限体積離散法では, 境界上の解がはっきりと定義されません. この方法では, 通常ではそのセルの中心の値と解釈される, 各セルの解の値を定義するだけです. そのため, 有限体積法が有用であるためには, ある種の再構成法が必要となります. 一般的には, 隣接するセルの値を考慮した局所補間法が用いられます(図3参照). 解と流束の高次の補間を行うためには, より多くのセル値を考慮する必要があります. これは煩雑なだけでなく, ローカルではない方法を必要とします.
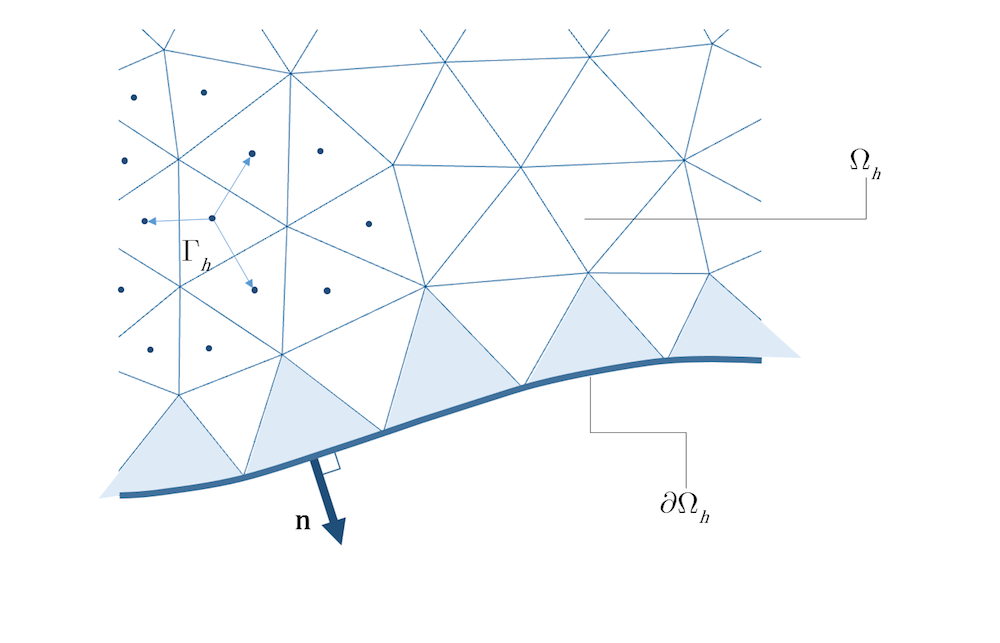
図3. セル中心有限体積法では, セルを中心とした点間の補間により流束ベクトルを構築します.
有限要素法で用いられる基底関数や, 有限体積法で用いられる流束の構造の種類によって, 異なる精度を得ることができます. 粗いメッシュで2次精度の手法を用いた場合, 細かいメッシュで1次精度の手法を用いた場合よりも精度の高い解を出します.
有限要素法のための線形テスト関数と基底関数は, 通常, 2次精度の方法につながります. 有限要素法は, 離散化に関して大きな柔軟性を持っています. 例えば, 2次基底関数を使用することは非常に簡単です. また, 解の再構成や補間も必要ありません. この方法は非常に対称的で, 境界上の流束境界条件を自然で直接的な方法で課すことができます. 粗いメッシュで2次精度の手法を用いた方が, 細かいメッシュで1 次精度の手法を用いた場合よりも精度の高い解を得ることができます.
有限要素法で一般的に使用される保存的なガラーキン定式化は, 局所的な保存性を保証します. しかし, 局所的な保存性を保証しないにもかかわらず, より高い精度のために移流定式化が好まれることが多いです. さらに, ガラーキン定式化では通常安定化項が必要であり, 適切に補正しないと局所的な保存性が損なわれる可能性があります. さらなる欠点は局所的なフラックスを制御できないことで, 離散化を安定化することと局所的な保存性を保証することの両方が困難になります. この場合, 安定化とは, 離散化のアーチファクトである非物理的な振動を除去することを意味します. 局所的な保存性確保と移流支配の系に対する安定化は, 弱形式を直接あるいは間接的に編集し, テスト関数を変更することで行うことができます (たとえば, 上流型ペトロフ–ガラーキン定式化や SUPG). しかし, これらの方法は計算量が多くなってしまいます.
先に述べたように, 有限体積法は, 区分けされた一定の有限要素の基本関数に対応しており, 場合によっては流束の高次補間スキームを使用します. これにより, 1 次または2次の精度を持つ手法につながります. 有限体積法の局所的な記述は, 局所的な保存につながります. これはこの方法の魅力的な特徴の一つです. これは, 各セルの正味の流束がバランスしていることが保証されているということです. また, 対流が支配的な流れの問題に対して, 離散化を安定化させるための自然で直接的な方法にもつながります. いわゆる上流化の安定化やその他の安定化は, セル間境界の流束を修正することで自然に得られます. アップウィンドは, 対流流束の方向に離散化の非対称性を与えます.
有限要素法では, 異なる次数の基底関数に対して手法を定式化できるという利点があります. 基底関数の次数が高ければ, 高次で正確な手法が得られ, 与えられたメッシュでの精度を向上させることができます. 有限体積法ではゼロ次の基底関数を使用しますが, 代わりに流束に高次の補間スキームを使用することができ, これも精度の向上につながります. 高次の手法を使用すると, 結果としてシステムが大きくなり, 同じメッシュでの解答時間が長くなります. しかし, その分, 精度も高くなります. つまり, 性能を比較する際には, 一定の精度に対する性能を比較する必要があるのです. セル数や要素数ではなく, 同じ精度の流体問題を異なる手法で解くために必要なCPU時間とメモリを測定することが, これらの異なる手法の性能を比較するための正しい方法なのです.
今後の有限要素法
COMSOLでは, CFDのための有限要素法を主に扱っていますが, これは私たちの専門分野だからです. この15年間で, 不連続なテスト関数と基底関数を用いた有限要素法の開発において, 研究コミュニティで大きな成果が得られました. これが冒頭で述べたDG法です. これらの方法では, テスト関数は各要素に局所的であり, 弱方程式は各要素で成立します. 局所的な保存は自動的に得られ, 高次の離散化は簡単です. 解の再構築も, 有限体積法と同等のゼロ次法を除いて必要ありません. さらに, 要素境界上の局所的な流束は定式化の自然な部分であり, これは安定化が簡単であることを意味しています. DG法の欠点は, 余分な自由度の導入量が比較的多いことです. このため, 離散化を無駄なく行い, より少ない自由度を得ることができる, いわゆるハイブリッドDG法が研究されています.
FEMとFVMの比較についての結論
これまで述べてきたように, 有限体積法と有限要素法にはそれぞれ長所と短所があります. 大規模な流体問題を効率的に計算するためには, 時間ステップの効率的で安定した処理, 暗黙的およびある程度明示的な時間ステップの効率的な実装, 大規模な連立方程式の解法など, 他にも多くの重要な側面があります. まだまだやるべきことはたくさんありますし, さまざまな手法や技術を進化させる可能性も秘めています.
私たちCOMSOLは, 有限要素法を用いた最高かつ最新の技術を提供するために常に研究しています. また, マルチフィジックスだけでなく, CFDのようなシングルフィジックスのアプリケーションでも, 一般的に最良の手法を開発することに取り組んでいます.



コメント (0)