よくある質問のひとつに, 次のようなものがあります. “特異点の存在下で応力を評価する最善の方法は何か？” これに対する最も正確な答えは, 評価しないことです. しかし, これは実用的なエンジニアリングにはほとんど役に立ちません. このブログでは, 特異応力場の特性を詳しく見て, いくつかの可能なアプローチについてご説明します.
これは, 以前のブログ“有限要素モデルにおける特異点: レッドスポットへの対処”の続報です. この記事では, 構造力学モデルにおいて特異応力が発生する場合とその理由についてご説明しています. この記事は特異応力に関する入門であり, このトピックを初めて学ぶ方にお勧めします. 特異応力場の扱い方の詳細については, こちらの記事を読み進めてください.
特異応力場を詳しく見る
まず, 特異応力場と応力集中との関係をより詳細に解析することから始めましょう. 応力集中も特異応力場と同様, 幾何学的な不連続面に現れるという点では類似しています. 応力集中と特異点の違いは, 前者の場合, 最大応力に境界があることです. 例えば, 有限要素 (FE) モデルで十分に細かいメッシュを使用すれば, 正確な値を得ることができます.
通常, 機械設計者は, できるだけ大きな半径のフィレットを導入することで, 応力集中を軽減しようとします. 応力集中部のピーク応力は, 通常, 応力集中係数K_{\mathrm t}と適切に選択された公称応力の積として記述されます. フィレットの場合, K_{\mathrm t}に次の式が使用されることがあります.
ここで, \rhoはフィレット半径, L_\mathrm{char}はフィレットで終わるノッチの特徴的な長さです.
この式の背景は, 大きなプレートの楕円形の穴における応力集中の解析解です. ここで, L_\mathrm{char}は楕円の大きい方の半軸の長さです.
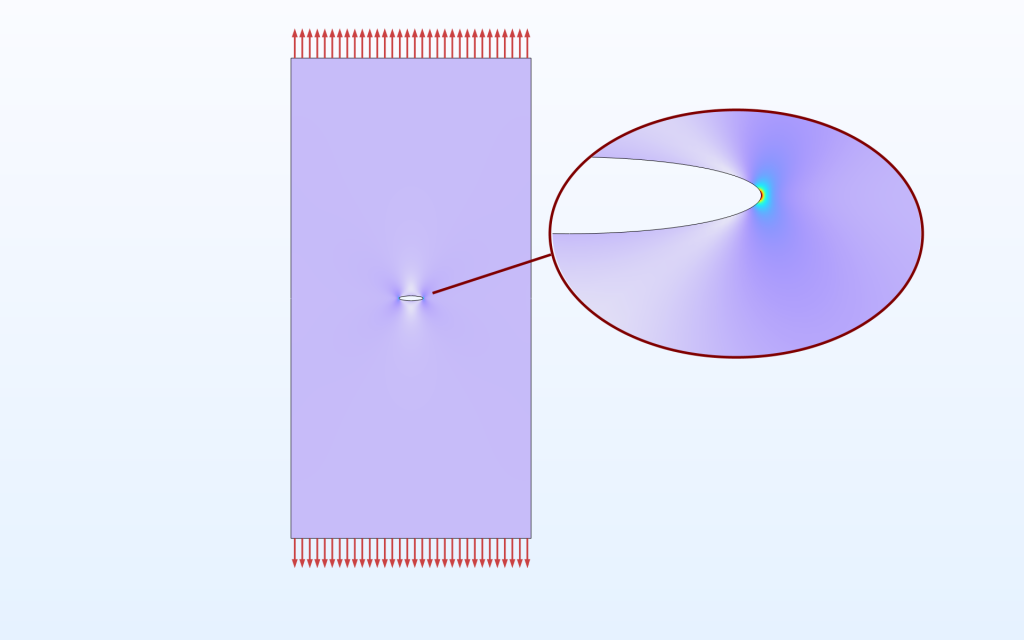
楕円形の穴が開いた大きなプレート.
ほとんどのノッチでは, 特性長さを推測することが難しいため, この式はK_{\mathrm t}に対する大まかな推定値を提供するためにしか使用できません. 重要なのは, 小さなノッチでのピーク応力が, フィレット半径の平方根の逆数として本質的に変化するということです. フィレット半径を適度に大きくすると, ピーク応力はさらに適度に小さくなるからです. 局所的な応力集中を減らそうとしたことのある技術者なら, おそらくこの事実に苦労したことがあるはずです.
極限応力集中は, ノッチ半径が限りなく小さい亀裂先端で発生します. 弾性体では, 亀裂先端に近い応力場とひずみ場の解はよく知られています. これらは, 亀裂先端からの距離rの平方根に反比例して変化します. 応力場は一般に次のように表されます.
ここで, K_I, K_{II}, K_{III}はそれぞれモードI (開口), モードII (せん断), モードIII (引き裂き) の応力集中係数です. 関数 f, g, hは, 亀裂先端近傍の極角 \thetaの三角関数からなります. (詳細な定義については, こちらを参照).
驚くべき結論として, 亀裂先端に十分に近ければ, 亀裂の実際の形状や亀裂が存在する部品に関係なく, 亀裂先端周辺の応力場は同じように見えます.
線形弾性破壊力学の仮定の下で, モード I における破壊の基準は K_I = K_{Ic}となります. ここで K_I = K_{Ic}は材料パラメーター (破壊靭性と呼ばれる) です. このようにして, 無限応力を明示的に用いることなく, この特殊なタイプの特異点を持つジオメトリを解析することができるのです. この概念は, 以下で一般化します.
ここで, ジオメトリに特異点に近いものがある場合を考えてみましょう. つまり, 角やフィレット半径の小さな亀裂などです. これが, このブログで取り上げる状況です. 遠目には, ノッチと特異点の違いを見分けることはできません. 次の例で, この意味を説明します.
引張状態の長いノッチ付きストリップの2Dモデルを使用します. 左の垂直エッジに沿って対称条件を追加することで, 同じモデルを使って内部スリットを調べることもできます.
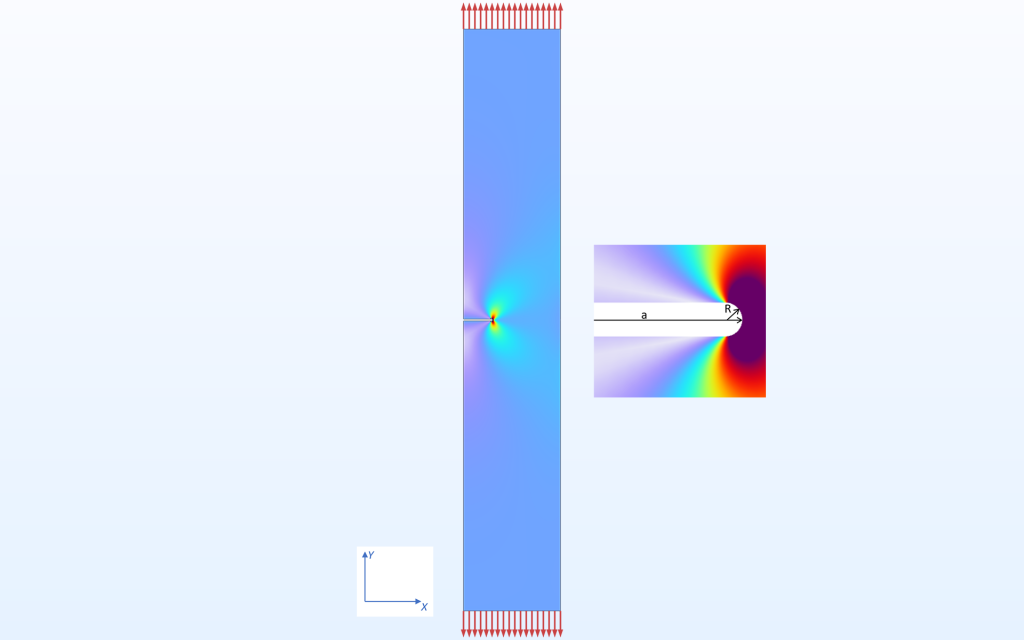
ノッチ付きストリップの応力分布. モデルはノッチの深さ (a)とノッチ半径(R)に基づいてパラメーター化されています.
まず, 鋭い亀裂の場合, このジオメトリの応力集中係数は次のように表されることがわかります.
ここで, aは亀裂の長さ, \sigmaは印加応力 (この場合は1Pa), Wはストリップの幅です. 関数fにはいくつかの表現方法があります. ここでは, 次の式を使用します.
この式は, このブログで亀裂解と呼ばれるものを与えます.
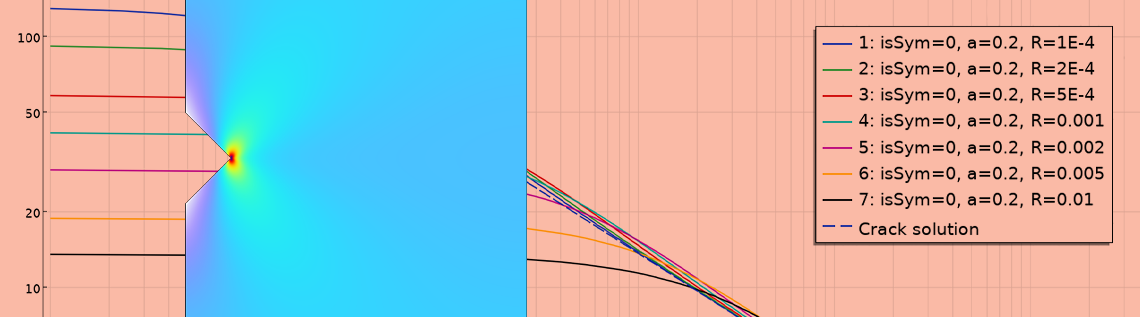
リガメントに沿った応力分布 (ノッチ先端からx方向に伸びる) が, 短いノッチといくつかの異なるノッチ半径についてプロットされています. 対称性のため, 1つの応力成分cのみが非ゼロとなっています.
異なるノッチ半径に対するノッチ先端からの距離の関数としてのリガメントに沿った垂直応力. 破線は同じ深さの亀裂の理論解を示しています.
ある領域では, 応力場が亀裂解で得られたものと非常に似ているという興味深い観察があります. すなわち, log(応力)-対-log(距離)線図の直線です. ノッチに近づくと, ノッチは亀裂ではなくノッチであるため, 応力は制限されます. 予想通り, ピーク応力は 1/\sqrt{R}に比例します.
先端から遠いところでは, それが亀裂であろうとノッチであろうと, 亀裂の局所応力場解はいずれにせよ有効ではありません. しかし, 非常に近くから遠くまでの領域では, 私たちの視覚的な観点からも, 物理学や数学の観点からも, ノッチ先端の真の形状を推測することは実際には不可能です.
さて, なぜこれが重要なのでしょうか? ノッチの形状がわかれば, 特定の距離の応力を見るだけで, そこにかかる応力を知ることができるのです. これについては, 後で詳しくご説明します.
次のステップとして, さまざまな異なるノッチ半径とノッチ長さに対する応力を同じ図にプロットしてみます. ただし, 横軸はノッチ半径 Rで正規化します.
ノッチの深さと半径を変えた場合の, ノッチ先端からの距離の関数としてのリガメントに沿った垂直応力.
ここでわかるように, 一定の勾配領域は, ノッチ先端から先端半径よりも小さい距離, 例えば0.7Rから始まります. これは, 我々が対象としている問題の観点からすると, かなり近い値です. では, この領域はどのくらいの長さになるのでしょうか? それはノッチの詳細ではなく, ジオメトリの大きさによって変わります. プロットの別の正規化であるリガメントの長さ(W-a)を使うことで, この情報を得ることができます.
上と同じプロットだが, 距離をリガメントの長さで正規化したもの.
結論として, この場合の一定勾配領域は, リガメントの約10%まで広がっています. それ以上離れると, 応力場はもはや亀裂解によってではなく, よりグローバルな特性によって制御されるようになります. 特定のジオメトリに対するこの領域の大きさには, そのジオメトリに特有の長さスケールに依存します.
亀裂解の応力場を使って, ノッチ先端のピーク応力を予測できるかどうか調べてみましょう. まず, 大きなプレートの楕円形の穴に戻ります. 楕円形の穴 (幅 a, ノッチ半径 R) におけるピーク応力と, 亀裂 (長さa) の応力集中係数との比は次のようになります:
R << aとすると, ピーク応力は応力集中係数で次のように表すことができます.
つまり, 応力集中係数が計算できれば, 丸い亀裂先端の応力を次のような式で求めることができるということです.
ここで係数\ beta は構成に依存する1のオーダーの数です. 上の例でこの仮説を試してみましょう.
以下のプロットでは, 式
はノッチ半径をパラメーターとして, ノッチ深さの関数として示されています. エッジノッチと中央スリットという2つの異なるジオメトリが使用されています. 後者の場合は, モデルに対称条件を加えることによって得られます.
エッジノッチがある場合の係数\beta.
中央スリットの場合の係数\beta.
ご覧の通り, ノッチ半径が小さい限り, 想定される乗数\betaの実際の値はどちらの場合も1.2に近くなります. ノッチ半径が大きく, ノッチ長さが小さい場合には, 亀裂との類似性はあまり良くありません. R << aを用いた単純化は有効ではありません.
これらのグラフを作成するために, K_Iの解析値を使用しました. K が不明な実際のケースでは, ノッチから離れた位置での解を使用してK_Iを数値的に決定することができます.
実際のところ, どのような鋭い角でも, 応力場がr^{-p}として減衰する領域があります (ここで, rは角からの距離です). これまで, 理想的な亀裂ではp = 0.5であることを見てきました. どのような開口角の場合でも, pの値は下図のようになります.
開口角の違いによる応力減衰特異点の強度. 45度°, 90°, 135°の値が強調表示されています.
曲線は超越方程式 \sin \left ((1-p)(2\pi-\alpha) \right) +(1-p) \sin(2\pi-\alpha) = 0を解くことで描かれ, \alphaは開口角です.
完全を期すために, 内角との間に張力のあるストリップのFEモデルで超越方程式の解を確認できます. このモデルは, 角の開口角を使用してパラメーター化されます.
開口角が90°の場合の内角のあるモデルにおけるフォン・ミーゼス応力.
リガメントに沿った垂直応力. 角の先端からの距離はリガメントの長さで正規化されています. 破線は, 上記のp値を用いた理論解を示しています.
ご覧の通り, 応力対距離線図にはほぼ直線の領域があり, 角の近傍では理論的な傾きとほぼ一致しています.
もう一つのタイプの特異点は, 材料の不連続性によって引き起こされます. 実際には, 幾何学的特異点と一緒に発生することが多くあります. ここでは, 引張を受ける棒材における純粋な材料不連続に焦点を当てて解析します.
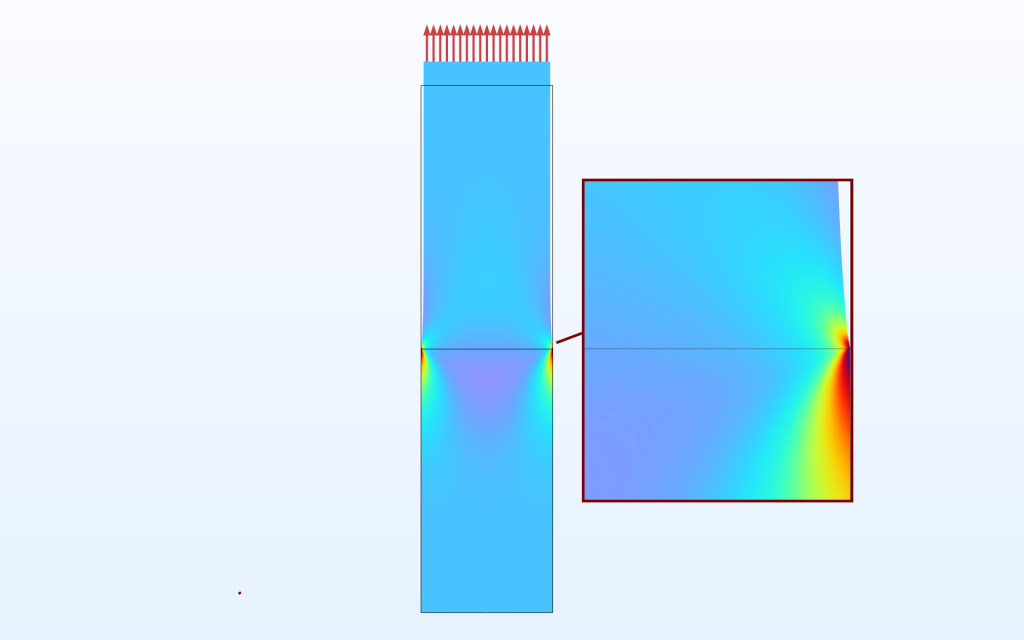
下部が上部より硬い棒. 荷重方向の応力をプロットしたもの.
この最初のプロットですでに確認できる一般的な特性がいくつかあります.
- 自由表面上に特異点が生じています.
- 硬い材料の応力は, 柔らかい材料の対応する場所の応力よりも高くなっています.
これをより詳細に調べるために, 材料インターフェースからの距離の関数として応力の減衰を示すグラフを作成します.
自由境界に沿って, インターフェースからの距離の関数としてプロットした荷重方向の応力. 実線は軟質材料の結果, 破線は硬質材料の結果を示しています. パラメーターrは2つのヤング率の比です.
このlog–log図でも, 直線が見えます. 応力が距離r^{-p}に応じて変化しているということです. 力‘p’はどちらの材料でも同じです (同じ色の実線と破線は平行です). 特異点の強度は, 2つの弾性率の比とポアソン比の値の両方によって制御されます.
上の表面プロットの (誇張された) 変形形状を見れば, これは物理的に解釈できます. 同じ荷重に対して, 柔らかい材料の方が硬い材料よりも伸びるということです. つまり, 柔らかい材料では荷重方向のひずみが大きくなるのです. これはまた, 2つの材料のポアソン比が同じであることを考えると, それに対応して横方向の収縮も大きくなることを意味します. しかし, この収縮は2つの材料のインターフェースでは抑制され, 局所的な応力特異点が生じます.
を選択すれば, この特異点は完全に消えます.
結論として, 材料遷移はほとんどの場合, 特異点を引き起こします. また, この場合, 不連続性の近傍には, 応力がべき乗則に従って減衰する領域があります.
ここまで, FEモデリングで発生する最も一般的なタイプの特異点を研究し, これらに共通の性質があることを確認しました. それは, 特異点近傍の応力は, 距離に対してべき乗依存性を持つということです.
溶接評価
疲労に対して安全な溶接部を設計することは, 工学の重要な分野です. 一般的に正確な応力評価は不可能であるにもかかわらず, 故障を予測する体系的な方法を提供するために多くの研究が費やされてきました. この場合, 問題の原因は主に, 溶接部の実際のジオメトリが不明であることです. 正確な局所ジオメトリによって, 溶接部に応力特異点が生じるか生じないかも異なります. さらに複雑なことに, 溶接部には欠陥が隠れていることがよくあります. 例外は, 高い品質が要求される場合で, その場合は溶接部を研磨し, 何らかの非破壊検査方法でチェックします. しかし, ほとんどの場合, 溶接部の詳細な局所応力解析を行うことは意味がありません.
3つの異なる局所ジオメトリを持つフィレット溶接.
溶接部の応力評価については, ブログ“溶接部の疲労寿命を予測する方法”で紹介しています.
溶接解析の詳細を掘り下げるよりも, ここで興味深いのは設計思想です.
- 溶接止端自体ではなく, 適切に指定された位置で応力を計算する.
- その応力の許容値を設定する. これは通常, 実験的に行う必要があります.
- 許容応力値は, 応力を評価する方法と位置に依存するので, 真の材料特性ではありません.
ペンと紙で計算していた時代には, 局所的な影響はすべて無視されていました. 許容応力値はそれを考慮する必要があり, そのため低くなっていました. 最新のFEベースのアプローチでは, 応力集中の一部 (グローバルジオメトリに起因する部分であり, 局所的な溶接部のジオメトリには起因しない) が考慮されています. その結果, 応力はより高くなることが許容されますが, それでも純粋な材料試験が示す値よりはかなり低くなります.
有限要素法では, シェルモデルは通常, 求めている応力を返しますが, 固体力学モデルでは, 溶接部の疲労解析を行う際に不要な応力の詳細を把握することができます.
推奨されるアプローチ
FEモデルに特異点が含まれる理由として, 根本的に異なる理由がいくつかあります. 例えば, 次のようなものです.
- 前述のブログで述べたように, 境界条件は特異点を誘発します. このような特異点が解析に問題を引き起こす場合は, 境界条件を改良することで解決できます.
- 鋭角が導入されるのは, 局所的なジオメトリのスケールが大きすぎて, グローバルなスケールでフィレットをモデル化するのは合理的ではないからです. この場合, 真の特異点は存在せず, 明確に定義された応力集中があります. 最も正確なアプローチは, サブモデリングを使用して, グローバル解から局所的応力状態を決定することです. グローバルモデルでは, 応力集中の近傍でべき乗減衰する応力場の振幅を使用して, どこに重点を置くべきかを知ることができます. もう 1 つの可能性は, 近傍場の応力場に関する知識と, それが局所的な応力集中とどのように相関するかに関する知識を組み合わせて, その局所的な応力集中を推定することです.
溶接評価から得たパターンを踏襲しつつも, それを局所的状況に合わせて調整します. そのためには, 過去の設計のうち, どれが失敗し, どれが失敗しなかったのか, 基盤となる実験が必要です. そして, 過去の設計を分析し, その実験と相関する評価方法を見つける必要があります.
これらの設計のFEモデルを設定することから始め, 応力またはひずみ場が, 局所的なノッチの詳細によっても, よりグローバルなジオメトリによっても制御されない範囲にある領域を特定するようにします. 少なくとも基準を定めようとしている間は, サブモデリングを使用する必要があるかもしれません.
どのような基準を使うべきかは, 通常, 明らかではありません. 相対的な比較を行うだけであり, 計算された数値を物理的な強さの値と関連付けるわけではないので, 多くの選択肢が考えられます. 例としては, 以下のようなものがあります.
- 量は簡単に評価できる.
- 量は, 解析における不確実性にあまり敏感であってはならない.
- 可能であれば, 量は物理的に適切であるべき. 例えば, 材料が脆い場合, フォン・ミーゼスのような等価応力基準を使用するよりも, 最大主応力または主ひずみに注目した方が良い.
- 疲労が問題となる場合, 量は荷重の反転に対して敏感でなければならない.
- 可能であれば, 応力基準ではなくひずみ基準を選択する. なぜなら, ひずみは変位から直接計算されるからです. 次に, 応力はひずみの組み合わせを使用して計算されます. つまり, ひずみテンソルに不正確な部分が1つでもあると, 応力テンソルのすべての要素に伝播することになります.
- COMSOL Multiphysics®ソフトウェアでは, 安全性機能を使って, ユーザ定義基準を含む多くの異なる基準を評価することができます.
一般的な場合, 特異点のべき数は不明です. しかし, ある領域では, 関心のある量が次のように変化することが分かっています.
Kとpの値は, 最小二乗近似によって求めることもできますし, 単純にlog–log図の直線部分上の2点の値を用いることもできます. pは, ある種の特異点に対して一定である性質と考える必要があるので, 計算された値を使って, アプローチの妥当性を確認できます.
pが既知であれば, 特定の構成におけるKの値を許容値と比較する必要があります. これは, 破壊力学における亀裂の扱い方と似ています.
パーセンタイル法
許容応力レベルを求めるもう一つの方法は, 基準体積の所定の割合 (例えば5％) で超過する値として基準応力を定義することです. この基準応力が許容値より低い場合, 設計は承認されます. この方法を用いることで, 特異点に近い評価の問題を回避することができます. 基準応力を超える体積を計算できることだけが重要であり, その体積の境界は, 解がよく収束する特異点からある程度離れたところになります.
この方法は単純に見えますが, 適用するためにはかなりの標準化が必要です. ここで問題となるのが, 基準体積の決定です. 構造の総体積を用いると, 低応力領域に材料を追加するだけで基準応力を減少させることが可能になりますが, これはもちろん意味がありません. 基準体積は, 例えば特異点近傍の特定領域の大きさに関連付けなければなりません. もう一つの欠点は, 最適化手法では応力の再配置を選択する可能性があり, その結果, ピーク応力を増加させながら基準応力を減少させてしまうかもしれないことです.
繰り返しになりますが, 似たような構造同士しか比較することはできません.
では, パーセンタイル法で応力値を評価する方法をご説明します. COMSOL Multiphysics®では, 5%の応力値を直接評価することはできません. 以下にて, 3つの代替方法をご紹介します.
方法1
単一の評価だけが必要な場合, 最速の選択肢は通常, いくつかの手動反復を行うことです. 積分演算子 (例えばintop1) を作成し, intop1(solid.mises>sRef)/intop1(1)のような式を評価するだけです. 基準応力 sRefを数回変更することで, すぐに指定されたパーセンタイルに対応する値を見つけることができます.
方法2
モデルメソッドを使ってメソッド1を自動化します.
方法3
以下に説明するように, 追加の方程式を設定して応力値を解くことができます.
解くべき方程式は以下の通りです.
ここで, \sigma_\mathrm{c}は計算された応力です. これは, フォン・ミーゼスのような等価応力であったり, 第一主応力であったり, その他のものであったりします. もちろん, ひずみやエネルギーの基準にも同じ手順を用いることが可能です. 基準体積は V_\mathrm{ref}, \betaはパーセンタイルを示しています. 積分内のブーリアン式は, 真の場合は1に, 偽の場合は0に評価されると想定されます.
計算で扱いやすいスケーリングを得るためには, 方程式を次のように書き直すのが良いでしょう.
積分は, 最初の方法と同様に, 積分演算子を用いて計算することができます. グローバル方程式ノードを使ってこの方程式を実装する簡単な方法を以下に示します.
残念ながら, これはうまくいきません. 不等式は微分できないので, ヤコビアンを形成できません. 剛性行列はこの方程式に対してゼロを含むだけです. しかし, 手動で有限差分微分を導入することで, この問題を回避することができます. この式は長く, COMSOL®の方程式ベースのモデリングをある程度理解している必要があるため, 以下の追加情報セクションに詳細に説明しています.
以下は, 意図したパーセンタイルが得られる応力を求めるための, 修正されたグローバル方程式です.
ここで, ユーザー定義パラメーターdSは, 応力増分であり, 追加情報セクションでは \Delta \sigmaで示されています.
このアプローチの例として, 先ほどと同じノッチ付きプレートの例を使用します. 基準体積はプレートのサイズに依存しないはずなので, 例えば, ノッチを囲む円を選ぶことができます. この場合, 円の半径は, 構造の以下の特徴的な長さに基づいて選択できます.
- 幅: 1 m
- 最小亀裂長さ: 0.1 m
- 最小リガメント幅: 0.3 m
- 最大ノッチ半径: 0.01 m
ノッチ先端を中心とした半径0.05mの円に基づく参照体積は, 構造の境界から遠く離れているだけではなく, ノッチ自体の詳細からも遠くなっています.
スリット深さとノッチ半径の異なる値に対して, 基準体積の5%で超える応力レベル.
スリットの深さのすべての値について, 5％パーセンタイル応力は基本的にノッチ半径に依存しません. スリットの深さにのみ影響されます. これは, 局所的な, 場合によっては特異な応力場の詳細に対する影響を避けるという基本的な考え方と一致しています. 鋭い先端とフィレットのどちらを使用しても, 同じ結果が得られます. 本質的に, このアプローチは応力集中係数と同じ情報を与えてくれます. 同じタイプのフィレットを持つ構造を比較する場合, この方法は適切な基準を提供します.
追加情報
この式には2つの項があります. 最初の項は残差を, 2番目の項はヤコビアンを作成します. これは, 一般的に高度なモデリングで使用できる解法です. 例えば, 正確なヤコビアンを作成するのにコストがかかる場合, 類似の式を使用して, 近似ヤコビアンとともに正しい残差を作成することができます.
数カ所で使われるnojac(expr)演算子は, 与えられた式に対してヤコビアン寄与が生成されないようにします.
ヤコビアン項には係数 (sRef-nojac(sRef)) が掛けられます. この式は常にゼロと評価されるので, この部分から残差は生じません. sRefのそれ自体に対する導関数は単純に1であり, 式の残りは導関数の対称有限差分式
となります.
ここで, \Delta \sigmaは応力の有限の変化です. \displaystyle \int_V (\sigma_\mathrm{ref}+\Delta \sigma<\sigma_\mathrm{c}) \; dV によって計算される体積が\displaystyle \int_V (\sigma_\mathrm{ref}<\sigma_\mathrm{c}) \; dV と大きく異なるという性質を持ちながら, できるだけ小さくなるように選択される必要があります. 適切なレベルは, 1つの要素にかかる応力の変化が, 結果として得られる基準応力\sigma_\mathrm{ref}の等値面近傍で \Delta \sigmaとなる場合です.
さいごに
理論的な観点からは, 特異点における勾配やフラックス (ひずみや応力) を評価することは不可能であるにもかかわらず, この問題にアプローチできる体系的な方法があります. しかし, そのような方法には, 慎重に選んだ臨界量を解釈するのに十分な実験的証拠が必要です.
このブログで使用したモデルをダウンロードするには, 下のボタンをクリックしてください.
コメント (0)