熱音響エンジンは, 熱入力から音響エネルギーを生成します. レシプロエンジンやガスタービンなどの一般的なエンジンとは異なり, 熱音響エンジンは可動部品を使用しないため, 構造が非常にシンプルです. このブログでは, 流体の線形化された振る舞いをモデリングするための強力なインターフェースの1つである熱粘性音響インターフェースを使って, 熱音響エンジンの動作メカニズムをどのようにモデリングできるかを紹介します.
熱音響エンジンの仕組み
150 年以上前, Pieter Rijke 教授は, 熱音響学の先駆的研究とみなされる興味深い現象を報告しました. ガラス製の円筒管に金網を入れて垂直に持ち, 下から火で加熱しました. 火を消した後, シリンダーからしばらく音が鳴り続けるのが観察されました. (参考文献 1) この装置は現在ではライケ管としてよく知られているため, 共振現象の一例として使用されているのを見たことがある人もいるかもしれません. しかし, 共鳴はさておき, そもそも音はどのようにして発生するのでしょうか？
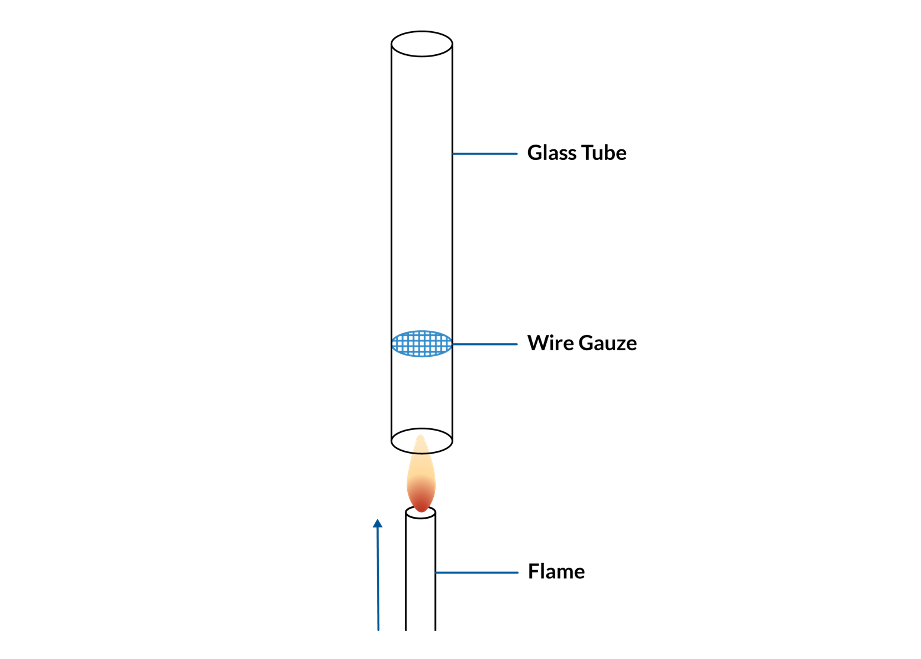
ライケ管の設定
その秘訣は, 温度変化とチューブ内の流体の動きの相互作用です. 加熱された金網が空気の自然対流を引き起こし, パイプ内に安定した流れを生み出します. したがって, 金網の上の空気は金網の下の空気よりも暖かくなります. パイプ内の定常半波音響共鳴では, 空気は音響周期の異なる時間に金網を通って両方向に流れます. 空気が金網を通過すると, 金網は加熱されます. 金網の下の空気は上の空気よりも冷たいため, 流れが下向きよりも上向きの方がより多くの熱が伝わります. 持続的な音場を得るには, 音圧が正のときに流体が加熱されるように, 熱放出が圧力場と同相である必要があります. 定在波では, 加熱を引き起こす速度場は圧力場とは位相が異なります. ただし, 金網の周囲の粘性境界層によって引き起こされる影響により, 熱の放出は速度場に比べて遅れます. この位相遅延により, 熱放出が部分的に圧力場と同位相になり, 結果として共鳴が持続します. パイプを横に向けると対流が止まり, 共鳴が持続しなくなります. パイプを逆さまにすると, 音圧が負のときに伝達される熱が最大になるため, 音場は維持されずに減衰します.
これは, 熱と音響エネルギーの間のエネルギー変換の一例です. 実際, 装置全体が熱音響エンジンの動作原理を示しています.
熱音響エンジンには, 音が伝播する閉管状の通路があり, 作動流体を加熱または冷却するために熱交換器が通路内にあります. 熱音響エンジンは定在波または進行波を使用しますが, ライケ管は定在波のみを使用します. 進行波エンジンは, 圧力と流体変位間の位相遅れにより, 定在波エンジンと比較して優れた性能を実現すると期待されています. このブログでは, 主に進行波エンジンのモデルを見ていきます.
進行波を利用した熱音響エンジンの原理を考えてみましょう. 波がどのように機能するかを理解するには, 下の図で流体の小さな塊の動きを確認してください. 音波は縦波なので, 左側から高圧の進行波が来ると, 荷物は右側に押されます. 同様に, 左からの低気圧が流体塊に到達すると, 流体塊は左に引っ張られます.
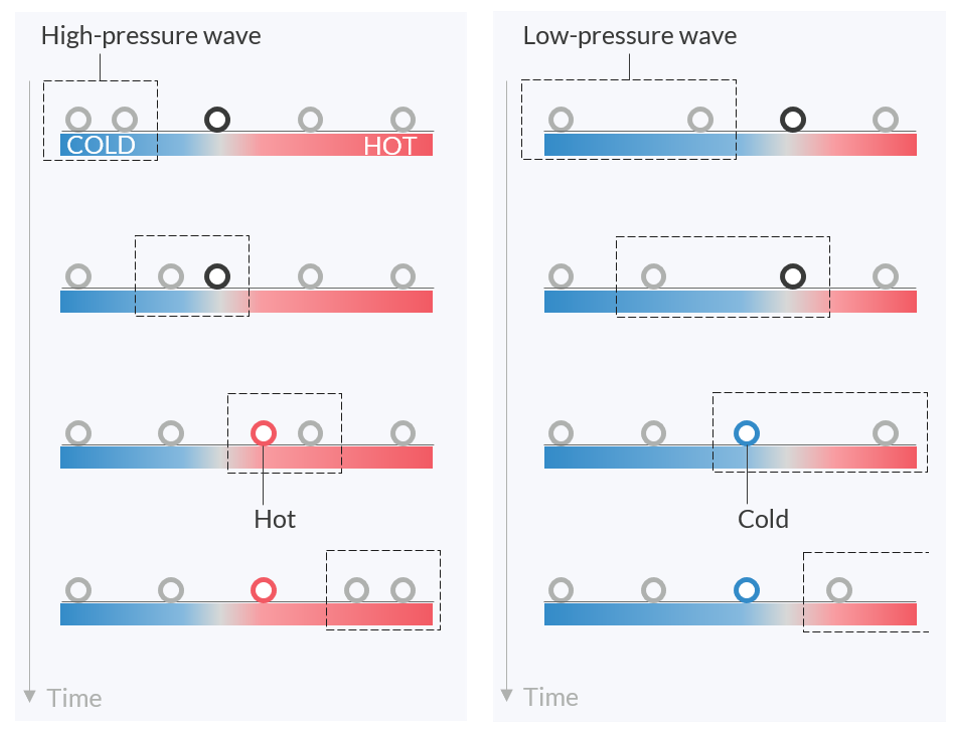
流体中の小包が左から来る進行波の下でどのように移動するか. 波の仮想領域は点線のボックスで表されます. 隣接するプレートに適切な温度勾配があると, 高気圧に押されれば荷物は常に高温の領域に移動し, 低気圧に引っ張られれば低温の領域に移動します
次に, 波の進行方向に沿って加熱したプレートをチューブに入れることを考えます. プレートの右端を加熱し, 左端を適度な温度に保つと, プレートには温度勾配が生じます. 温度勾配は, 小包が右へ動くと小包を加熱し, 左へ動くと小包から熱を吸収します. 区画は右に移動するときに最も圧力が高くなるため, 区画の加熱は圧力の最大値を押し上げます. 同じように, 区画が左に移動するときの熱吸収は, 圧力の最小値も減少させます. このような温度の周期的な上下が区画の動きを同期させ, 最終的に波の振幅を大きくします. すべての区画が連鎖して圧力波を伝え, 熱交換によって波にエネルギーを加えます. プレート内の温度勾配は波の伝播と同じ方向であるべきで, そうでなければ波は単に減衰するだけです.
エンジンの逆サイクルを備えた装置があるかどうか疑問に思う人に対する答えは “はい, あります” です. このシステムは熱音響ヒートポンプまたは熱音響冷凍機と呼ばれ, 音波を利用して熱を移動させることができます. 動作原理は単純です. 高圧波が小包に到達すると, 小包は圧縮され, その結果温度が上昇し, 小包は右に移動しながら隣接する物体に熱を放散し始めます. 逆に, 低気圧の場合, 荷物は熱を吸収して左に移動します.
ここでの説明は, あくまでも入門的なものであり, 熱音響エンジンの詳細をすべて含んでいるわけではありません. 熱音響エンジンについてのより詳細な情報に興味がある方は, 参考文献2を参照ください.
熱音響モデリングのための線形化方程式
新しいシミュレーションにはどの方程式系とどのインターフェースが適しているかを考えることが常に重要です. 現在のモデリング例では, 熱音響振動は音響波に関連しているため, 音響モジュールを使用して熱音響振動をシミュレートすることが合理的であるように思われるかもしれません. また, 学術分野は熱音響学と呼ばれているため, インターフェースは熱粘性音響学が適しているようです. 方程式とこのインターフェースの機能を確認して, 選択を検証してみましょう.
熱粘性音響インターフェースは, 時間領域解析で次の方程式を使用します.
ここで, \rho, \bm{u}, T, および p は, それぞれ密度, 速度, 温度, 圧力です. 添字 {\cdot}_0 は値が背景平均流量に属することを表し, 添字 {\cdot}_t の付いた変数は音響摂動を表します. 熱粘性音響インターフェースの支配方程式は, すべての 2 次摂動項がシミュレーションから省略できるという仮定に基づいて, ナビエ・ストークス方程式 (流体運動の正確な方程式) から導出されます. 背景平均流速はゼロです (\bm{u}_0=\bm{0}).
無視されている非線形性と, 線形化された方程式が関心のある現象をカバーしているかどうかに注意を払う必要があります. 熱音響エンジンの場合, 流体と熱交換器間の熱交換は拡散項 \nabla \cdot (k\nabla T_{\rm t}) で表されます. 音響振動による熱伝達は線形移流項 \bm{u}_{\rm t}\cdot \nabla T_0 で表されます. \bm{u}_{\rm t}\cdot \nabla T_0 項によって移流された高圧の冷たい流体は, 熱交換器内で \nabla \cdot (k\nabla T_{\rm t})によって加熱され, エネルギーは 3 番目の方程式によって増加します. これらの用語は, 系内の熱伝達の重要なメカニズムを説明しているため, 線形化された方程式はエンジンのモデル化に適していると思われます.
また, 時間変化する温度場と振動速度の結合を表す移流項がないことにも注意してください. \bm{u}_{\rm t}\cdot\nabla T_t. この結合された表現は, 振動によって引き起こされる過渡温度場の輸送を示します. 移流項はヒートポンプのシミュレーションにとって重要であり, 平衡時の温度勾配は振動の結果として決定され事前に利用できません. このような場合, 機能非線形熱粘性音響寄与を使用すると, モデルが熱粘性音響 (過渡)インターフェースで非線形項を考慮できるようになります. 非線形性のシミュレーションにはコストがかかる可能性があるため, 非線形機能は関連するドメインにのみ追加する必要があります.
COMSOL Multiphysics® でのモデリング
ここまで, 熱音響エンジンの基本的な動作メカニズムと, それらをモデル化するための関連支配方程式について説明しました. それでは, モデルの構築に進みましょう. ここに示されている例のモデルファイルには, アプリケーションギャラリでアクセスできます. 前のセクションで説明したように, 進行波熱音響エンジンをモデル化するために熱粘性音響インターフェースを使用します. 静止した背景温度場は均一ではないため, 伝熱インターフェースも使用できます. 2 つのインターフェースを同時に使用するのではなく, スタディ全体を 2 つのステップに分割できます. 背景温度場の定常ステップと, 音場の時間依存ステップです. 連成は, 熱粘性音響モデルノードの平衡温度として伝熱インターフェースの解を設定するだけで実行できます.
熱粘性音響インターフェースの境界条件に関しては, 熱交換器の壁が等温になるように設定する必要があります (T_{\rm t} = 0). この条件では, 高圧 (低温領域からの移流により T_{\rm t} がゼロ未満となる場合) で流体の温度が上昇し, 圧力が低いとき, 流体が冷却されます（T_{\rm t} がゼロより大きい場合）.
例 1: 単純なループ
まず, 単純なループで構成されるエンジンをモデル化します. 右側の通路に熱交換器があり, 通路全体が閉回路を形成しています. 定常温度は下図のように表示されます. 熱交換器の下部領域の温度勾配が目を引く場合がありますが, 私たちは熱交換器の小さな隙間の温度勾配に焦点を当てています.
単純なループ状エンジンの平衡温度 (左: システム全体, 右: 熱交換器周囲の拡大図). 熱交換器の狭い通路の下端は 493 K で加熱されます.
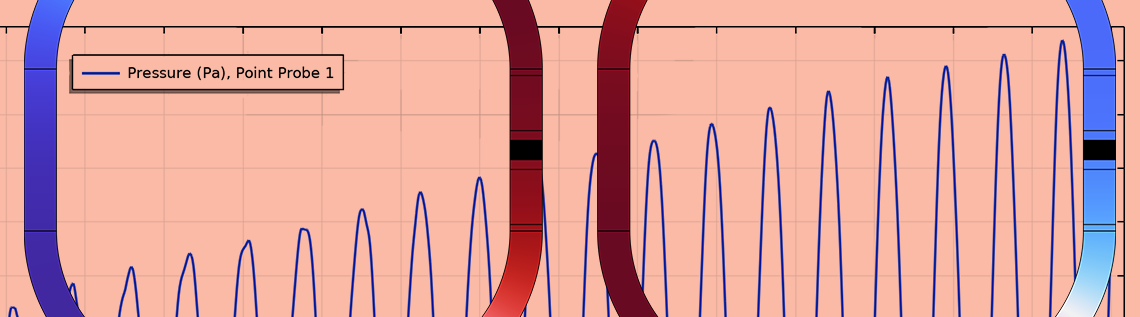
時間依存スタディステップでは, ループ内で振動を引き起こすことができるように, 圧力の初期条件として定在波が与えられます. シミュレーションが継続するにつれて, ポイントプローブ機能 (以下を参照) によって捕獲されるように, 振幅が増加します. 振動が成長し続けていることは明らかです. これは, 熱エネルギーが音響エネルギーに変換されていることを意味します.
ポイントプローブ 機能は, エンジン内の圧力を追跡するように設定されています. 圧力データは, 初期圧力分布として使用される定在波の圧力ノードに近い熱交換器内の点で取得されます.
では, エンジン内の圧力はどのようになっているのでしょうか？下の3つの図は, それぞれt = 0.281秒, 0.285秒, 0.289秒における圧力分布を可視化したものです. t = 0 sでは定在波が与えられていますが, しばらくすると分布は時計回りに回転し始めます. この波は, 熱交換器内の温度勾配と同じ方向に移動し, 最初の定在波の反時計回り成分は, そのためのエネルギー供給がないために減衰します.
興味深いことに, 反時計回りの波の励起は, シミュレーションの途中で温度勾配の方向を反転することでシミュレーションできます. モデルファイルでは, 定常スタディステップが t = 0.3 秒の逆転温度プロファイルで再計算され, 時間依存スタディはそれ以降の平衡温度の変化を反映します. それから. 時計回りの波は約 t = 0.6 秒まで残ります. その後, エンジン内に定在波状の分布が現れ, 最終的に波は反時計回りに伝播します.
圧力分布の履歴 (左: t = 0.281 秒, 中央: t = 0.285 秒, 右: t = 0.289 秒). 先ほど述べた熱音響効果により, 高圧領域も低圧領域も時計回りに移動します.
例 2: スタブを含むループ
単一ループに加えて, もう 1つの構成を確認します. 次の図は, 複雑なジオメトリを含む次のモデルの例を示しています. 幾何学形状は参考文献の実験設定を模倣しています. 3. モデルは 2D であり, 参考文献で説明されている熱交換器と同じ水力直径を持つように単純化されています. 右下端の分岐パイプ (スタブと呼ばれます) は, 将来の音響エネルギーの抽出のために追加されます. 例 1 と同様に, ループは熱エネルギーを音響エネルギーに変換するためにエンジン内で使用されますが, ここではエネルギーの一部をスタブで抽出できます.
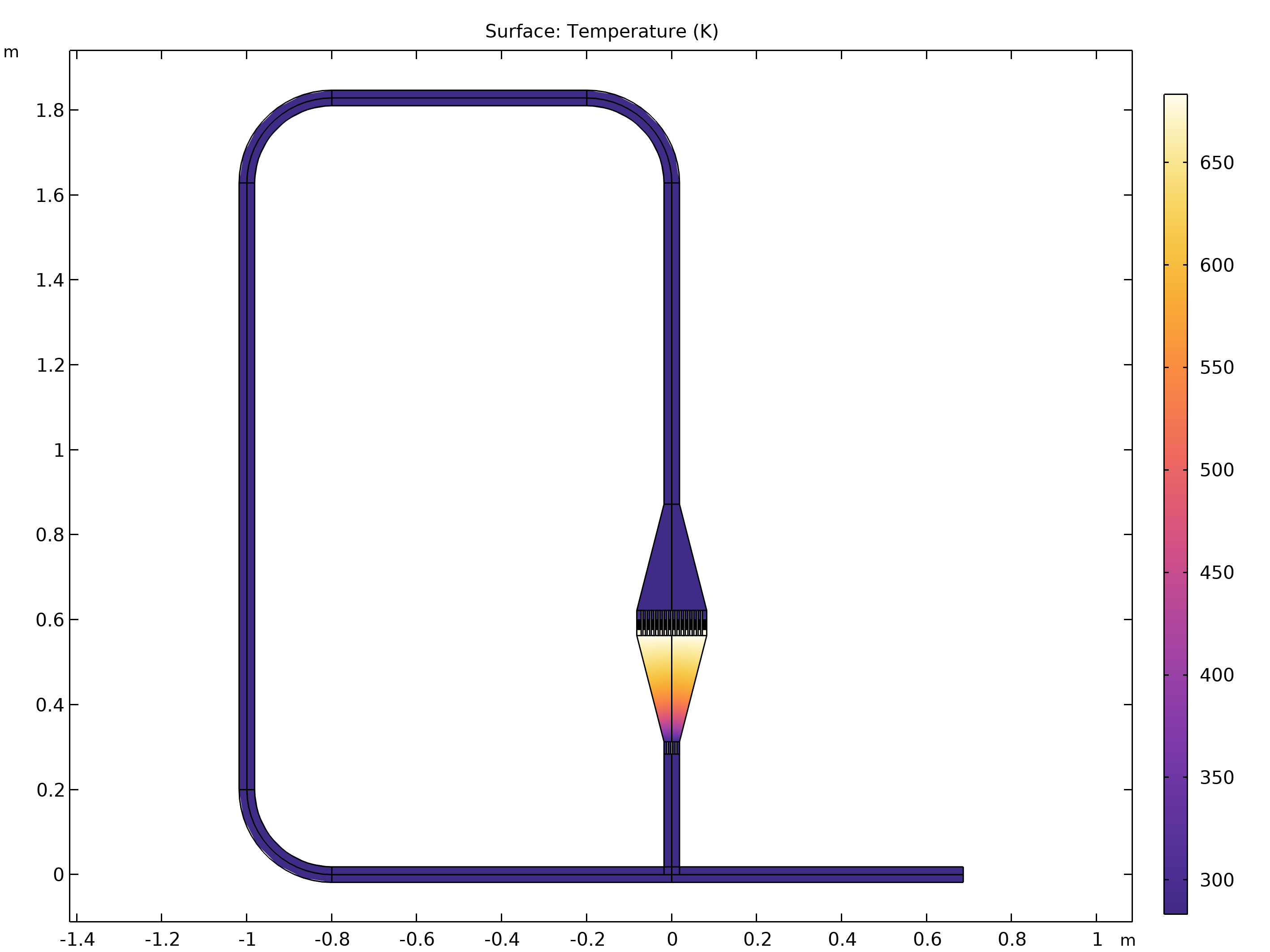
スタブのあるモデルの平衡温度. ジオメトリは, 参考資料 3 の実験設定を模倣しています.
エンジン内の瞬時圧力分布は下図のようになります. アーク長が 3.6 m に等しいところでは, 熱交換器の小さなギャップの粘性抵抗によって引き起こされる急激な低下があります. 特に, 圧力の振幅は位置に大きく依存します. これは, エンジン内で持続する粘性抵抗や定在波成分などのモデルの複雑さによるものです. 図では, max(|p|) とラベル付けされた絶対圧力の時間的最大値も各位置にプロットされています. 振幅が少し大きいように見えますが, このシミュレーションでは乱流がなく, いかなる摂動も線形であると仮定していることに注意してください. 空間最大値で無次元化すると, 近似振幅の分布max(|p|) は参考文献 3 の実験データおよび分析データとよく一致します.
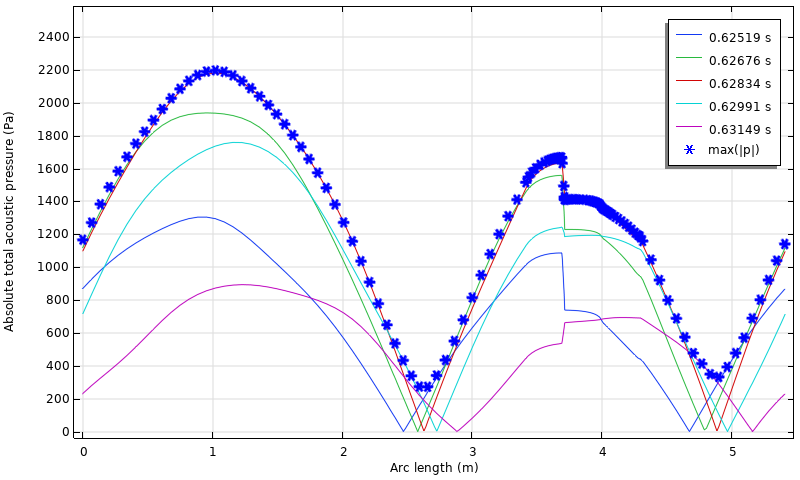
状態変数によって計算されるループに沿った瞬間的な圧力分布と近似振幅 max(|p|).
他の例
Rijke教授による実証以来, 熱音響学の理解は大幅に進み, エネルギーデバイスへの応用が現在活発に研究されています. このブログでは, 熱粘性音響インターフェースを使用して熱音響エンジンをモデル化する方法について説明し, エンジンの興味深い特性を可視化しました.
アプリケーションギャラリには, 物理分野にわたる多くのモデルがあります. 熱音響学に関連する 2つのモデルには次のものがあります：
- 簡単な熱音響エンジン. 定在波熱音響エンジンのモデルです. 複数のモデルファイルがあり, 2つの異なるアプローチで同じモデルを設定する比較を提供します. 熱粘性音響 (過渡)インターフェースによる線形摂動アプローチと非等温流による完全な非線形アプローチです. マルチフィジックスインターフェースです. 後者のアプローチでは, ナビエ・ストークス方程式を解き, 計算時間の増加を犠牲にして非線形性を考慮します.
- 熱音響エンジンとヒートポンプ. 定在波ヒートポンプのモデルです. 熱音響エンジンとは異なり, 熱音響ヒートポンプのシミュレーションでは, 熱輸送効果により温度が減少し続けるため, 非線形移流項 \bm{u_t}\cdot\nabla T_{\rm t} の計算が必要になります. モデルでは, 非線形性を考慮して非線形熱粘性音響寄与ノードが熱粘性音響インターフェースに追加されます. このモデルは, バージョン 6.2 の新機能である熱粘性音響-熱摂動境界カップリングも使用します. 固体温度は熱の汲み上げに応じて低下し続けるため, カップリングは通路内の振動流体と固体プレート間の熱交換をシミュレートするために使用されます.
参考文献
- P.L. Rijke, “LXXI. Notice of a new method of causing a vibration of the air contained in a tube open at both ends,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 17, no. 116, 419–422, 1859; https://doi.org/10.1080/14786445908642701
- G.W. Swift, Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, Springer, 2017; https://doi.org/10.1007/978-3-319-66933-5
- M. McGaughy et al., “A Traveling Wave Thermoacoustic Engine—Design and Test,” Letters Dyn. Sys. Control, vol. 1, no. 3, July 2021; https://doi.org/10.1115/1.4049528
コメント (0)