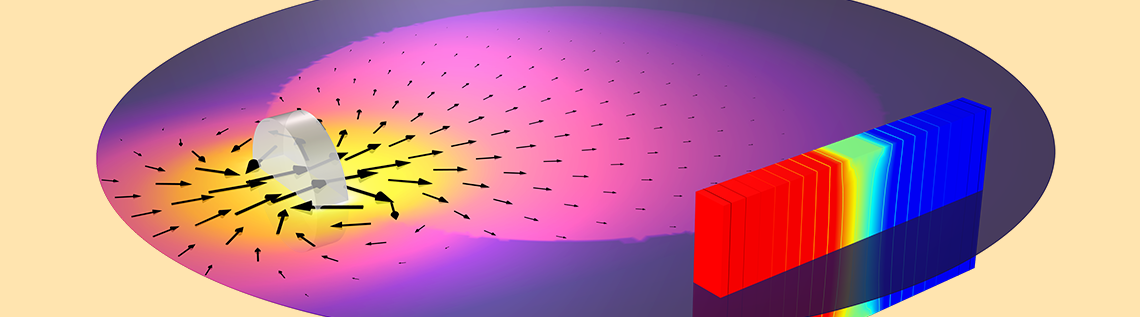
ホール効果センサーは, 一般的に位置検出に使用されるものです. 基本的な動作原理は, 近くの磁場による半導体センサーを通る電流の経路の偏向です. この電流のたわみは電位の変化を引き起こし, それを測定することができます. このデバイスのマルチフィジックスの性質にもかかわらず, いくつかの仮定さえ立てておけば, 実際には, COMSOL Multiphysics® ソフトウェアで非常に簡単にモデル化することが可能です. 詳しくは, 続きをお読みください.
ホール効果センサーの基本動作原理
まず, ローレンツ力の定義から始めます. これは, 電場\mathbf{E}と磁場\mathbf{B}を速度\mathbf{v}で移動する荷電粒子にかかる総力の式です. 電荷qの粒子にかかる総力は次のとおりです.
両端に電位差が印加され, 電流を流す半導体材料のスラブを見てみましょう. 均一なスラブの場合, 電流は2つの端子間を直線で流れます. ただし, ローレンツ力により, 近くの磁場がこの電流経路を偏向させ, 材料内の電位分布を変化させ, それを測定することができます. 典型的なホール効果センサーの場合, 磁場は近くの磁石によるものです.
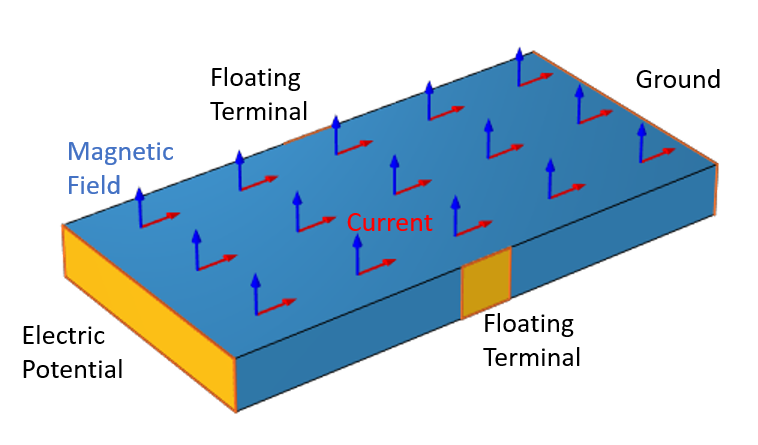
半導体材料のスラブ. 材料を通過する電流は磁場によって偏向され, 2つの浮遊端子間の電位が変化します.
計算モデルで使用する式については, 上の式から始めて, 半導電性材料を流れる電流密度を電場と磁場の関数として記述し, さらに2つの材料定数, 電気伝導度\sigmaとホール係数R_Hを加えます.
上記は行列‐ベクトル乗算として書き直すことができます.
つまり, ホール効果は, 磁場の関数である異方性電気伝導率を定義するだけでモデル化できます. 簡潔にするために, さまざまな資料での符号の規則とホール係数の導出についての説明は省略します. これが, 計算モデルに組み込む必要のある独自の構成関係です.
さて, 最も単純な状況では, 与えられた磁場を仮定し, それを使用して電気伝導率を計算できますが, ここで行うことは, 変化する磁場を計算し, それを使用して真のマルチフィジックスモデルを作成することです.
ただし, モデリングを開始する前に, 物事を単純化するためにいくつかの仮定を立てます. まず, 磁場の時間変化率は, 無視できるほど十分に遅いと仮定します. つまり, マクスウェル・ファラデーの方程式は次のように述べていますが,
\frac{\partial \mathbf{B} }{\partial t}はごくわずかであり, 無視できると想定するのです.
これは, 磁石の動きによって半導電性スラブに有意な誘導渦電流がないことを示すのと同じです. つまり, 材料内の電界は, 印加された電位と前述の構成関係のみに起因し, 磁界の時間変化に直接起因するものではないということです. この仮定により, 問題を静磁場の求解に絞ることができます.
次に, 半導体を流れる電流が十分に小さいため, 磁石による磁場と比較して, 半導電体自体が大きな磁場を生成しないと仮定します. これにより, 静磁気の問題がいわゆる電流のない形になり, 磁気スカラーポテンシャルを解くだけで済むのです. ただし, これらの仮定は, これから行うことには必要ないことにご注意ください. また, 近くのコイルなどからの電流による磁場を求解することもできます. これにより, 我々のモデルの計算コストは少しだけ高くなります.
最後に, 材料の導電率が十分に大きいため, RC時定数が私たちが注目しているどの時間変動よりもはるかに短いと仮定します. つまり, すべての時間微分項は重要ではないと想定しているため, いつでも電流モデルを純粋に静的な状況として扱うことができます. したがって, 電気的問題は, 磁場の関数である空間的に変化する異方性電気伝導率にもかかわらず, 定常電位方程式を解くことに限定されるのです.
そんなこんなで, いよいよモデリング開始です!
COMSOL Multiphysics® でのモデルの実装
下の画像のような状況を考えてみます. 小さな円筒形の磁石が回転する鉄の車輪に取り付けられています. その下に, センサーを表す長方形のドメインがあります. 縁に磁石を取り付けた回転鉄輪の下に設置したホール効果センサーの概略図.
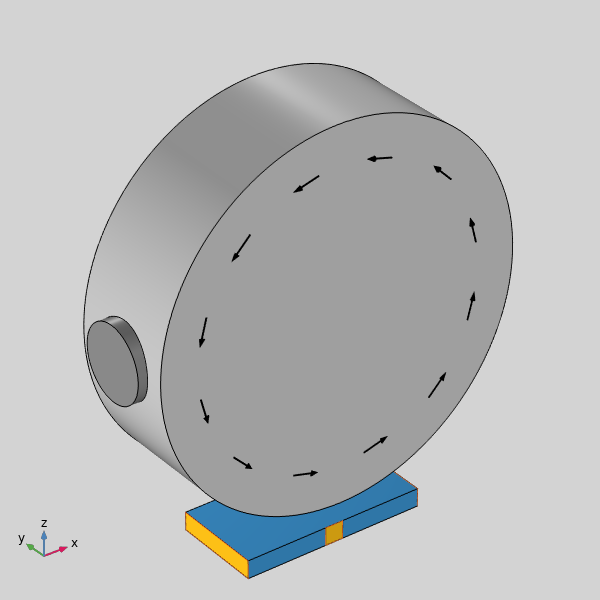
磁石を取り付けた回転鉄輪の下に設置したホール効果センサーの概略図.
まず, 磁場 (電流なし)インターフェースを使用して, 磁場を解きます. 上に示したドメインに加えて, これらを取り囲む空間と無限要素ドメインをモデル化します.
この問題を求解するにあたって, 磁場を計算することで, ホール効果センサーのモデルに進むことができます. 半導体領域では, 電流インターフェースを使用します. 接地条件と端子条件が材料の両端に適用され, 2つの浮遊電位条件が両側に適用されます.
電流インターフェースの使用法の簡単な紹介については, 抵抗性デバイスのモデリングに関する一連のチュートリアルビデオをご参照ください.
電気伝導率は, 先ほど計算した空間的に変化する磁場の関数にすることができますが, ホイールの回転も考慮する必要があります. 回転を考慮する最も簡単な方法は, パラメトリックスイープを実行することですが, 実際には, そこまでする必要はありません. 磁場はセンサーを介して回転していますが, センサー自体の影響を受けないと私たちは仮定しました.
このような状況では, 前回のブログで説明したのと同様に, 一般的な押出し演算子を使って, グローバルパラメーターAngleの関数として磁場を変化させるために, 回転マッピングを使用すればよいのです. ただし, この場合, ベクトル場を回転しているため, 3D回転行列を介してベクトル自体も回転します. 以下の2つのスクリーンショットは, 実装を示し, 回転した磁場変数のセットを定義しています.
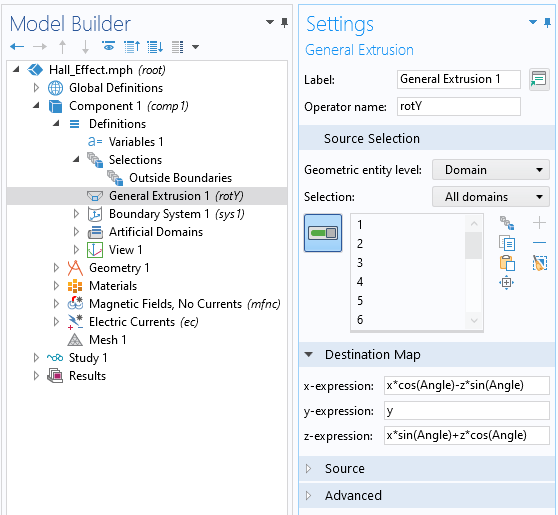
一般的な押出し演算子は, y軸を中心とした回転を定義します.
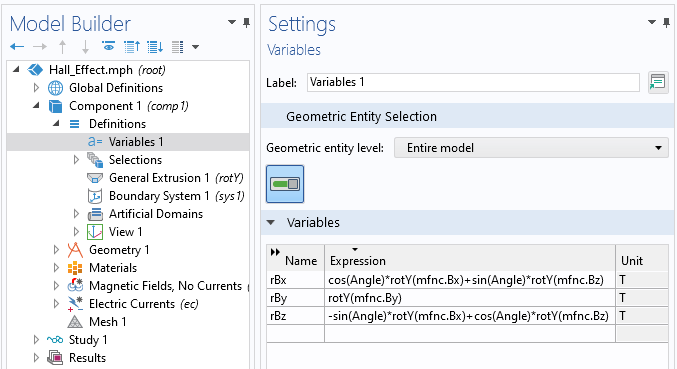
回転磁場成分を定義する変数.
回転した磁場成分が得られれば, 以下のスクリーンショットで示しているように, それを使って電流インターフェースで電気伝導率テンソルを定義することができます(下図).
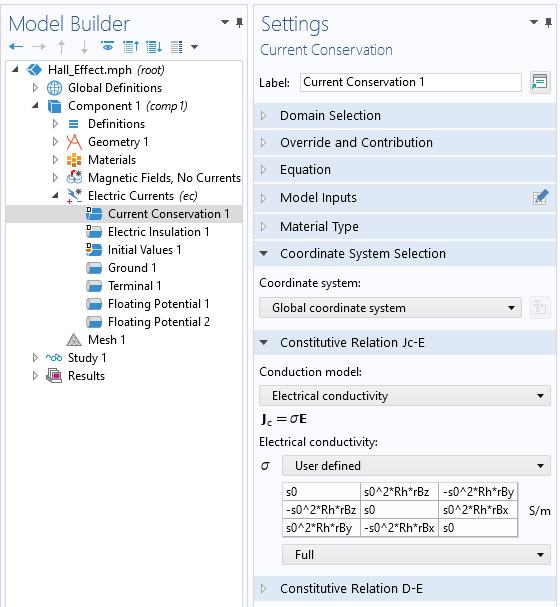
ホール効果センサー内の異方性電気伝導率の定義.
これで, モデルを解く準備が整いました. 最初に定常磁場を解き, 次に, 下のスクリーンショットに示しているように, 補助スイープによって磁場を異なる角度で回転させた状態で定常電流を解きます.
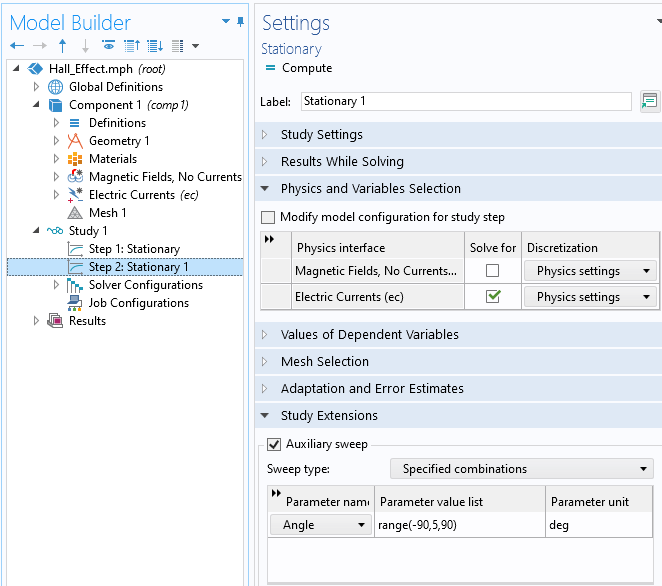
ソルバーの設定. 磁場は最初のステップで計算され, 2番目のステップでは, センサーの電位が磁石のさまざまな回転角に対して計算されます.
解いた後, 回転磁場をアニメーション化してアプローチを確認し, センサーの両側にある2つの浮遊電位境界条件間の電位差のプロットを調べることができます.
ホール効果センサーを介した磁石の回転と磁場のアニメーション.
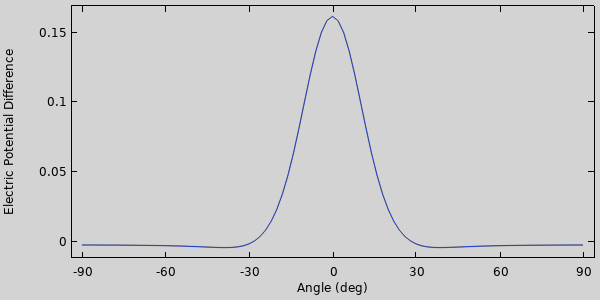
角度に対するセンサーの2つの浮遊電位間の電位の変動.
自分で試す
ホール効果センサーをモデル化する簡単な方法をご説明しました. モデル内の他の変数の関数である異方性電気伝導率を入力できるため, この種のシミュレーションは非常に簡単です. 一連の変換を介して場を手動で回転させることにより, 計算コストを大幅に削減することもできます. モデルは, 以下のリンクからダウンロードしていただけます.



コメント (0)