1669年の明るい夜, Erasmus Bartholinus 教授は, ベンチに置いたアイスランドの方解石の結晶片をのぞき込みました. 彼は, ベンチの上の文字を石で覆うと, 二重像のように見えることに気づきました. 観察された光学現象は複屈折と呼ばれ, 結晶から出てくる光線が2つの平行光線に分かれる現象です. ここでは, この効果のモデリングアプローチを示します.
異方性材料の理解
Erasmus Bartholinus が観察した, 結晶をまっすぐに通過する光線は, 通常光線と呼ばれます. 結晶を通過するときに曲がるもう1つの光線は, 異常光線です. 異方性材料, たとえば上記の石とベンチの実験で得られた結晶は, 有害ガスの検出から光子集積回路のビーム分割まで, さまざまな用途で使用されています.
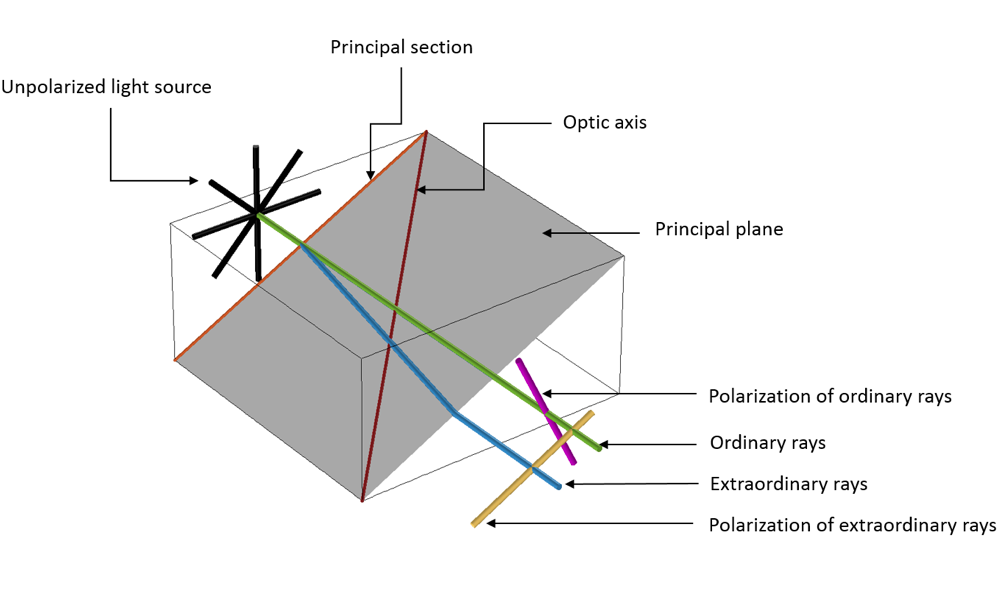
異方性結晶を伝わる通常光線と異常光線.
物理的な文脈では, 偏光されていない電磁光線が異方性誘電体材料を伝わると, 誘電体領域が偏光し, 電気双極子と呼ばれる電荷分布が生じます. この現象により, 異方性誘電体材料内に誘導場が生じ, 2種類の波が2つの異なる屈折率 (常波と異常波) を経験します.
常波は主平面に対して垂直に偏光し, 異常波は主平面に対して平行に偏光します. 主平面は, 光軸と結晶内の2つの伝播方向によって広がります. この動作により, 波は異なる速度と軌道で伝播します.
シリコン導波路内での異方性の導入
以前のブログでは, シリコンについて, またその誘導体である二酸化シリコンが CMOS 製造技術との互換性によりフォトニック集積チップで広く使用されている理由について説明しました. 等方性特性を持つバルクシリコンは, フォトニック集積チップのプロトタイプの開発に使用されます. ただし, ビームの分割や偏光に基づく光学効果などの独特の光学特性により, 異方性は後の段階で影響を及ぼします.
シリコンフォトニクスの異方性は, 導波路の製造中のアニーリングプロセスにより意図せず発生します. コアとクラッド間の熱膨張の差により, 応力光学効果による形状の不一致が発生し, モード分割やパルスの広がりなどの効果が生じます. 異方性は, 二酸化ケイ素の多孔度を変えることで意図的に導入することもできます. これにより, 研究者は二酸化ケイ素 (n ~1.44) から空気 (n ~1) までの有効屈折率の範囲で作業できるため, 非常に感度の高い光センサーアプリケーションを実行する優位性が得られます.
光伝搬モード
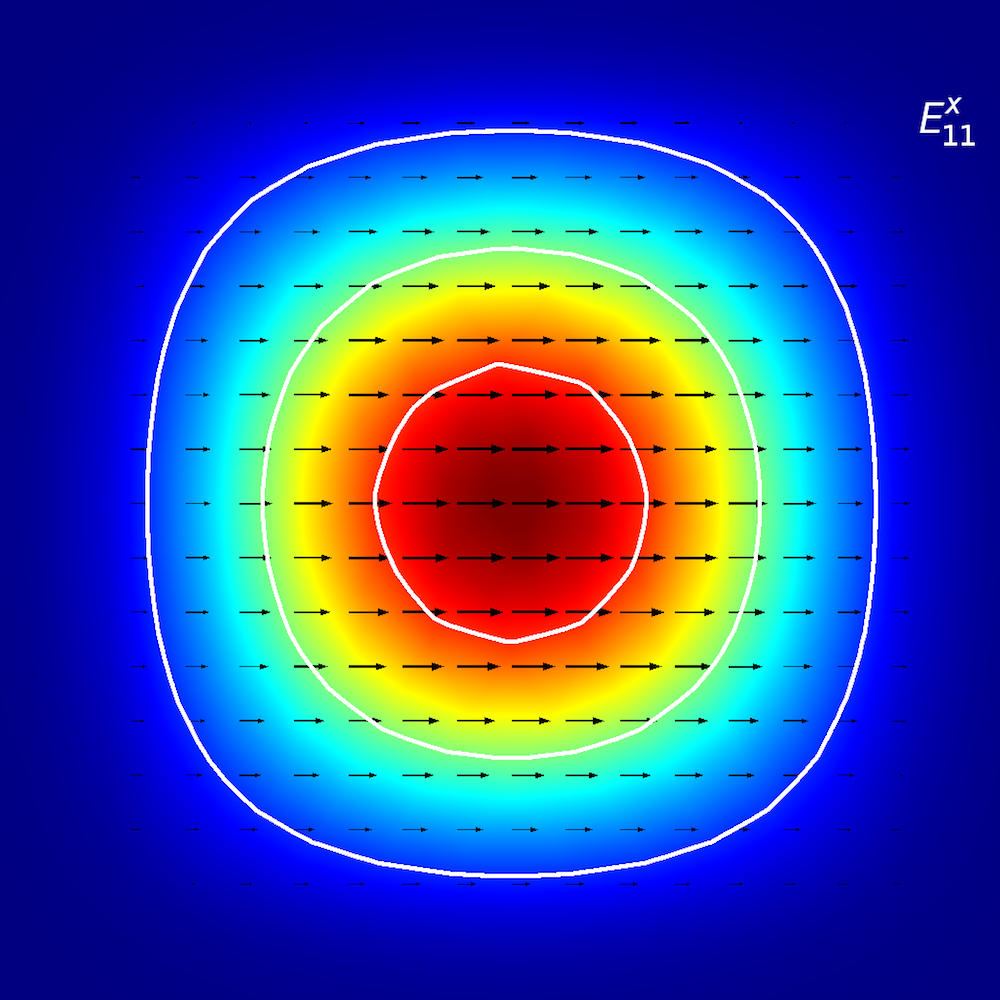
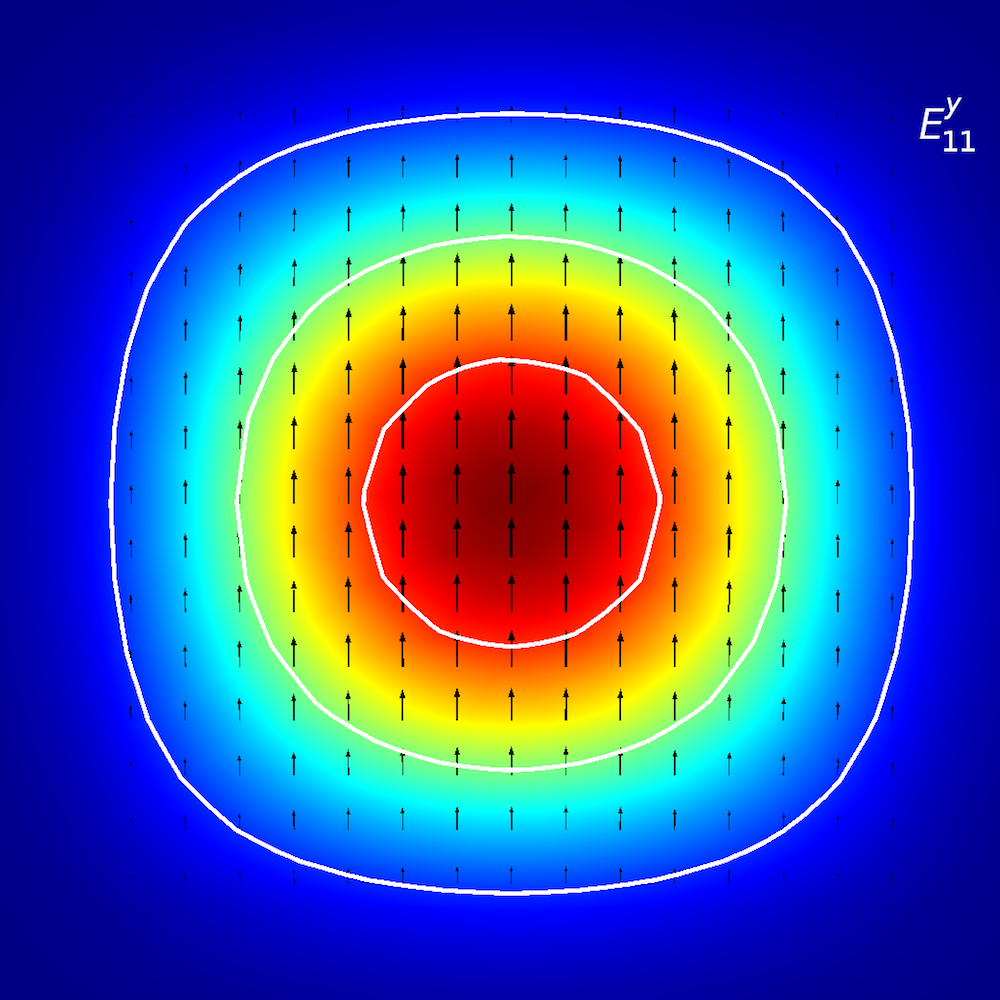
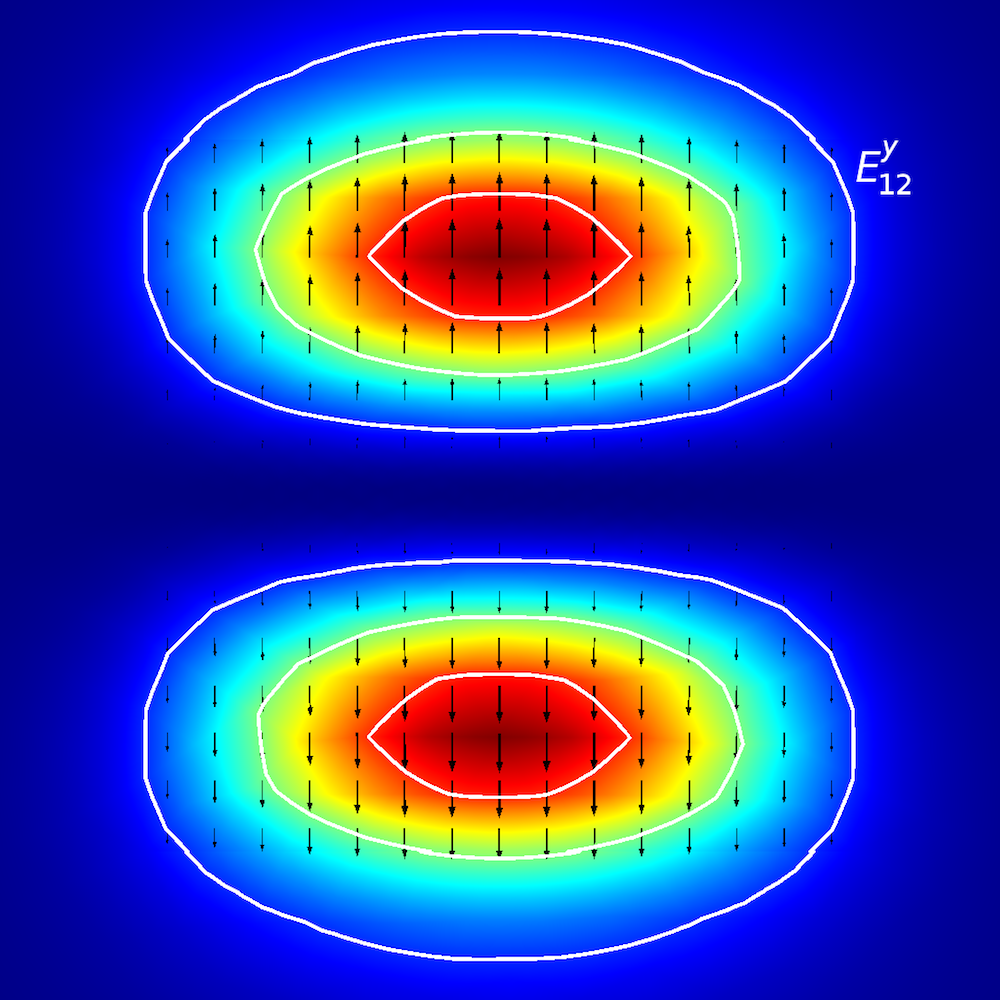
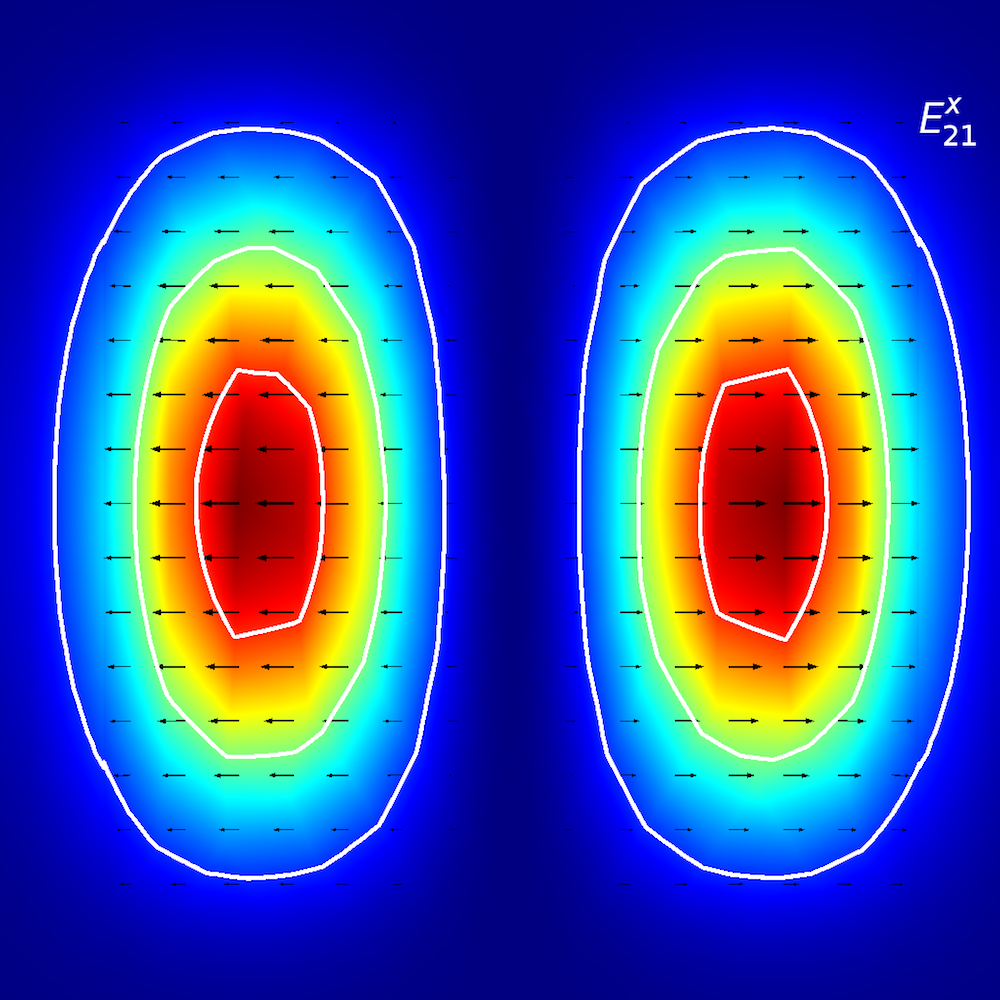
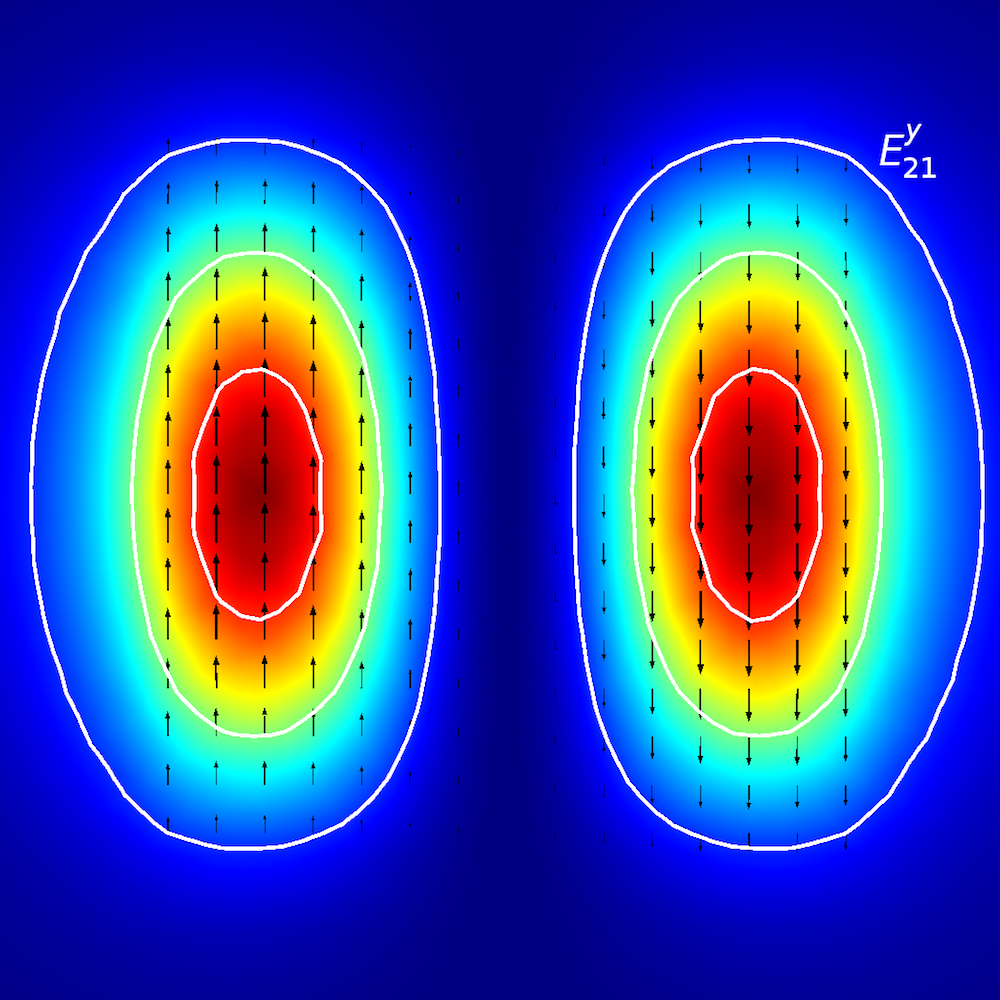
異方性媒体の定性分析を実行するために, 研究者は 平面導波路内で光エネルギーがどのように伝搬するか (伝搬モードとも呼ばれます) を解析します. 平面導波路では, モードを E^{x}_{p,q} および E^{y}_{p,q} という用語を使用して定義します (参考文献2). ここで, x および y は偏光の方向を表し, p および q は x 座標および y 座標の最大値の数を表します.
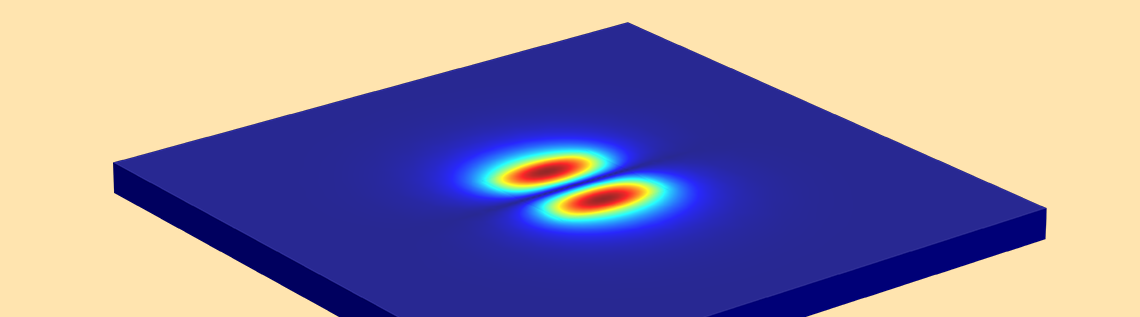
次のように想像してください. E^{x}_{2,1} 風景の上を歩いています (下図参照). 風 (偏波) は ±x 方向に沿っており, –x 方向から +x 方向へ移動すると, 2つの明確なピークに遭遇します. –y 方向から +y 方向へ移動すると, 両方のピークが同時に観察されます.
平面導波路のモード解析. 上の行, 左から右へ: E^{x}_{1,1} と E^{y}_{1,1}. 真ん中の行, 左から右へ: E^{x}_{1,2} と E^{y}_{1,2}. 下の行, 左から右へ: E^{x}_{2,1} と E^{y}_{2,1}. 矢印のプロットは電場を表します. 等高線と表面プロットは, 面外電力流れを表します (赤は高, 青は低振幅).
COMSOL Multiphysics® ソフトウェアでの異方性構造の解析
レーザー光源を使用して導波管に光線を通す前に, 導波管の指定されたコア/クラッド寸法内でどの光学モードが持続するかを知ることが重要です. COMSOL Multiphysics® ソフトウェアなどの完全なベクトル有限要素ツールを使用してモード解析を実行すると, 光学モードと分散曲線をそれぞれ定性的および定量的に解析するのに非常に役立ちます.
対角異方性の紹介
等方性材料でモード解析を実行するには, 単一の複素値の定義が必要ですが, 異方性材料の場合は, 完全なテンソル比誘電率アプローチが必要です. 電気誘電率は, 基本的に電場と材料特性を関連付けます. ここで, テンソルは, 以下に示すように, 対角項 (\epsilonxx, \epsilonyy, \epsilonzz) と非対角項 (\epsilonxy, \epsilonxz, \epsilonyx, \epsilonyz, \epsilonzx, \epsilonzy) の両方を持つ3行3列の行列を指します.
\epsilon_{xx}&\epsilon _{xy}&\epsilon _{xz}\\
\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\
\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}\\
\end{bmatrix}
ただし, すべての材料について, 誘電率テンソルの対角要素のみが非ゼロで, 非対角要素がすべてゼロである座標系を見つけることができます. この回転座標系の3つの座標軸は材料の主軸であり, それに応じて, 誘電率テンソルの対角要素の3つの値は材料の主誘電率と呼ばれます.
基本的に, 異方性結晶には一軸結晶と二軸結晶の2種類があります. 適切な座標系を選択すると, 誘電率テンソルの対角要素のみがゼロ以外となり, 光学特性の観点から, 一軸結晶は対角項のみを考慮します. つまり, \epsilonxx = \epsilonyy = (no)2, \epsilonzz = (ne)2 となります. ここで, no と ne はそれぞれ常屈折率と異常屈折率です. ただし, \epsilon_{xx}\neq \epsilon_{yy} \neq \epsilon_{zz} の場合, 二軸結晶と呼ばれます.
この議論をモデリングの観点から見ると, シリコンフォトニクス設計に関するブログの埋め込みリブ導波路の例を拡張できます. 正方形のコアとクラッドの長さがそれぞれ 4 um と 20 um の導波路の2D断面に対してモード解析を実行できます (下図参照). すべてのケースの動作波長は 1.55[um] と見なされます.

入口2D断面でモード解析を実行した3D埋め込みリブ光導波路の概略図. 強度プロットと矢印プロットは, それぞれ電場のモードと偏光を表しています.
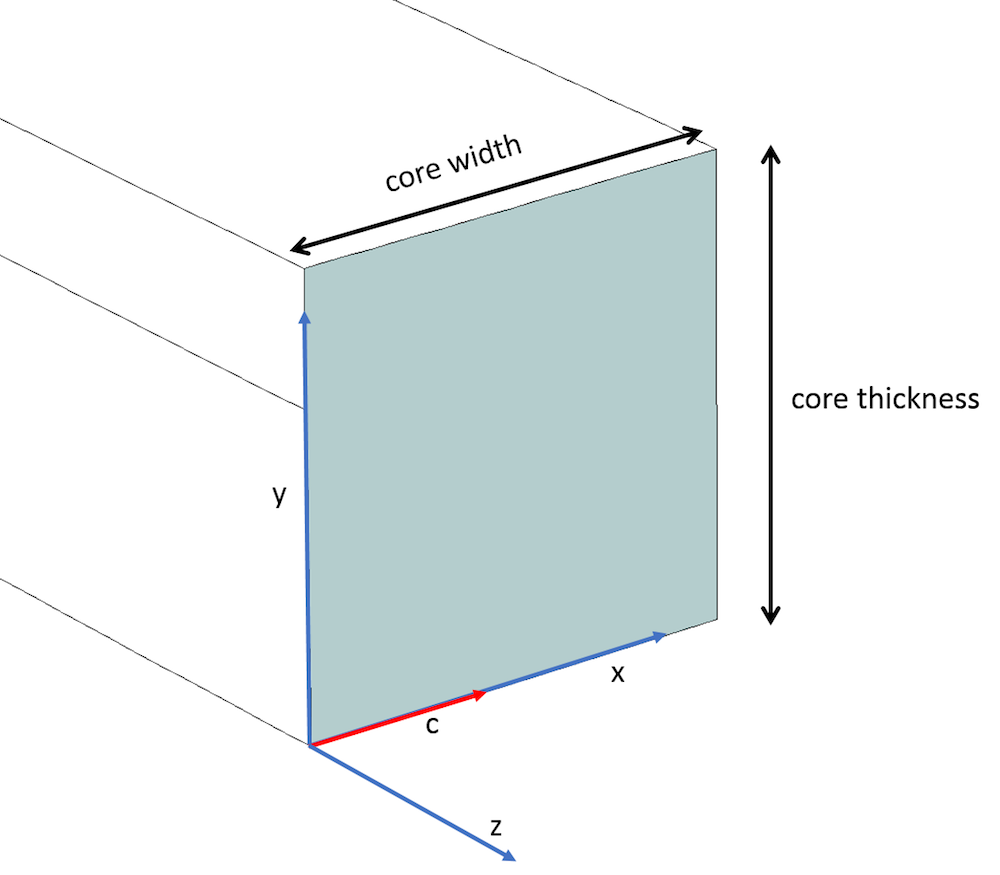
リブ導波路のコアは, x 軸に沿った光軸 (赤) と主軸 (青) を示しています.
単軸材料の典型的なケースでは, 光軸 (つまり, c 軸) が主 x 軸に沿っていると想定し (上図参照), 対角の相対誘電率 \epsilonyy 項と \epsilonzz 項 (c 軸に直交) を通常の屈折率の2乗 (~1.51992 ~ 2.31) と見なします. c 軸に沿った \epsilonxx 構成要素は, 異常屈折率の2乗 (~1.47992 ~ 2.19) と見なされます (参考文献3による). さらに, 対角外項はゼロと見なされ (以下に示すように), クラッドは等方性比誘電率 (~1.43182) を持ちます. 導出される光学モードは, 上記に示した6つのモードです. 屈折率の違いに注意してください. nxx – nyy は複屈折と呼ばれ, nxx = \sqrt{\epsilon_{xx}} および nyy = \sqrt{\epsilon_{yy}} です.
\begin{bmatrix}
2.19 & 0 & 0 \\
0 & 2.31 & 0\\
0 & 0 & 2.31\\
\end{bmatrix}
対角要素を持つ比誘電率テンソル.
分散曲線
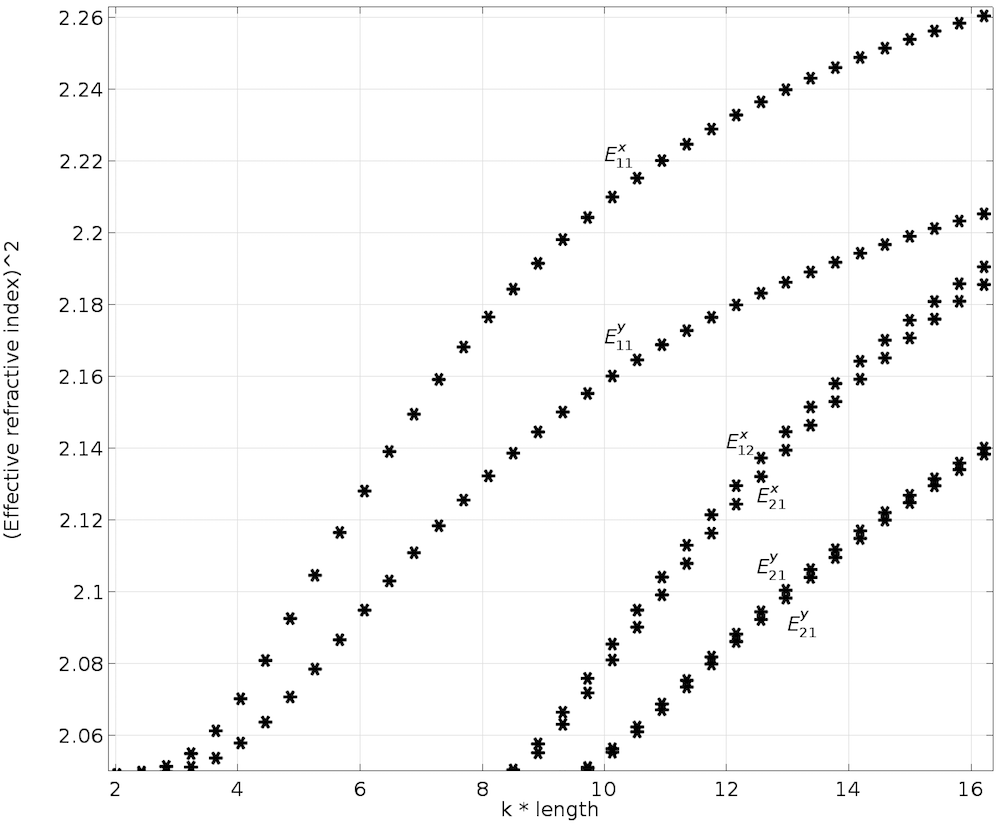
光モードを評価することで, 光導波路の動作を視覚的に理解できます. ただし, 分散曲線は定量分析を実行する場合にも便利です. 分散曲線は, 導波路の長さまたは動作周波数に対する有効屈折率の変化を表します.
対角異方性
次の図に示すように, 導波路の長さを 0.5 um から 4 um までパラメトリックにスイープしながらモード解析を実行し, 異方性コアの分散曲線を導き出します. 先に述べたケースを想定し, コアの対角異方性項 (つまり, \epsilonxx = 2.19, \epsilonyy = \epsilonzz = 2.31, およびすべての非対角要素がゼロ) を使用します. 結果は Koshiba ら (参考文献3) の結果と比較されます.
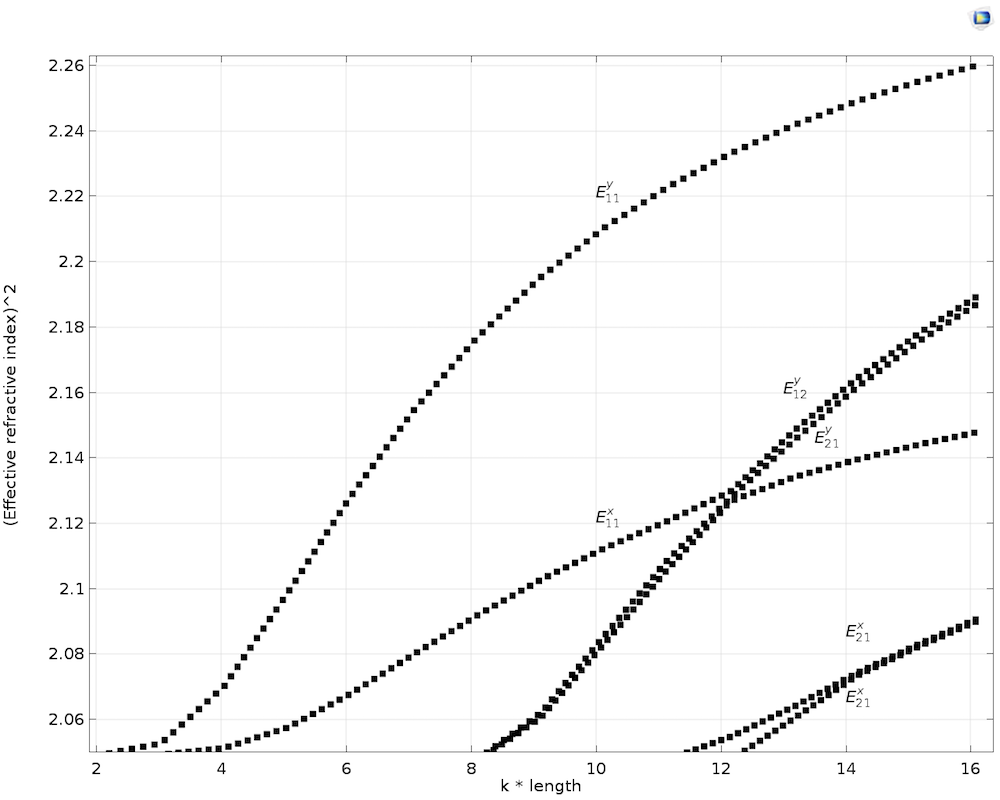
横方向異方性コアを持つ分散曲線.
非対角横方向異方性 (XY 平面)
光軸 (つまり, c 軸) が XY 平面にあり, x 軸と \theta の角度をなす場合, 対角成分 \epsilonxx, \epsilonyy, \epsilonzz, および非対角成分 \epsilonxy と \epsilonyz はゼロ以外ですが, 残りの成分はゼロです. 以下に示すように, 回転行列 [R] を使用して, 相対誘電率テンソル全体を評価できます. ここで, 回転行列 [R] は, XY 平面で c 軸を回転させるためのものです. \epsilonxx は異常屈折率 (~2.19) の二乗です. これは, c 軸が主 x 軸に沿っているためです. 一方, \epsilonyy と \epsilonzz は常屈折率 (~2.31) の二乗です. 非対角要素 \epsilonxy と \epsilonyz は, 以下に示すように, 行列の乗算から導出されます.
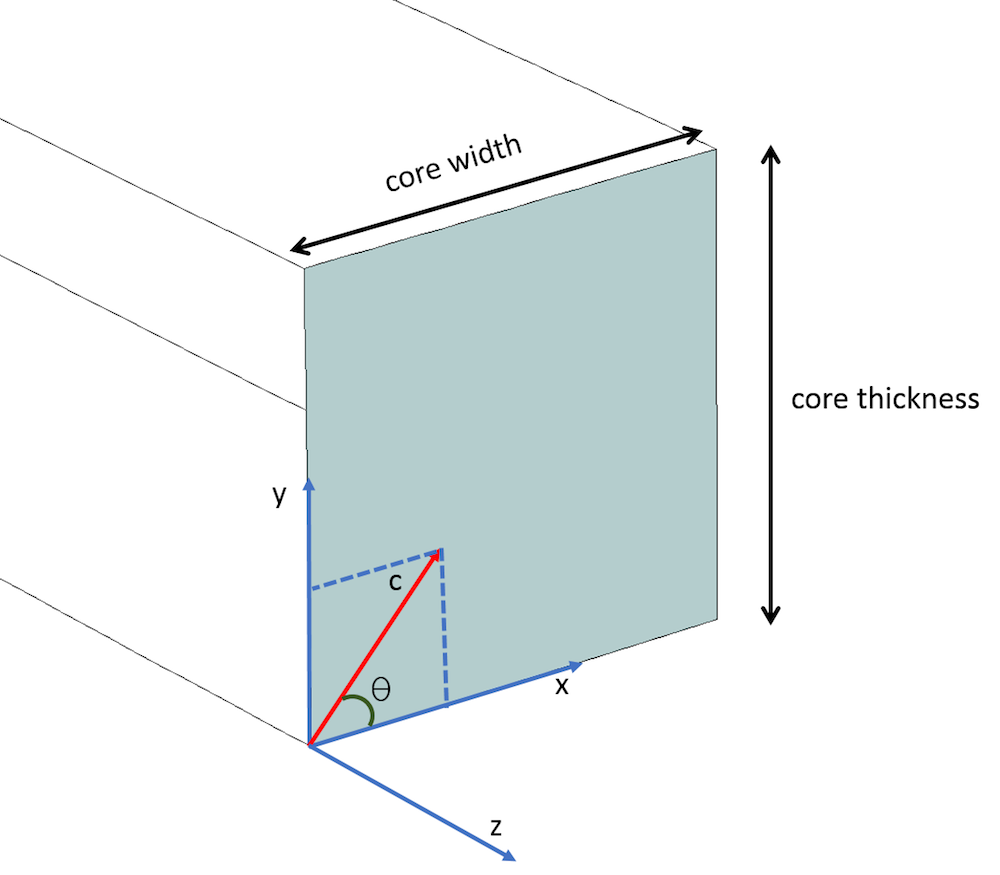
c 軸は XY 平面にあり, x 軸と \theta の角度をなします.
\begin{bmatrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz} \\
\end{bmatrix}
\begin{bmatrix}
cos(\theta) & sin(\theta) & 0 \\
-sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix}
(\epsilon_{xx}) cos^2(\theta) + (\epsilon_{yy}) sin^2(\theta) & (\epsilon_{xx}) sin(\theta) cos(\theta)-(\epsilon_{yy}) sin(\theta) cos(\theta) & 0 \\
(\epsilon_{xx}) sin(\theta)cos(\theta)-(\epsilon_{yy})sin(\theta)cos(\theta) & (\epsilon_{yy}) cos^2(\theta) + (\epsilon_{xx}) sin^2(\theta) & 0\\
0 & 0 & \epsilon_{zz}\\
\end{bmatrix}
相対誘電率テンソル ε は, XY 平面で c 軸を角度 \theta で回転させる回転行列とともに扱われます.
最後に, 以下に示すように, 光軸が主 x軸に対して 0, 15, 30, 45 度の角度をなす, 対角線外の異方性コアと等方性クラッドを備えた導波管のモード解析を示します. ここでは, 光軸の角度の変化に応じて面内磁場の方向が変化することが観察されます. 分散曲線は, 角度 \theta を 45° と見なし, コアとクラッドの長さを 0.5 um から 4 um までパラメトリックにスイープすることによってもプロットできます. 分散曲線は, 上で説明したように, 対角異方性の分散曲線に類似する傾向があります.
θ = 0° (左上), θ = 15° (右上), θ = 30° (左下), θ = 45° (右下) の非対角項を含むモード解析. この図は, 異なる回転角度におけるコア内の磁力線を表しています.
非対角縦異方性 (YZ 平面)
最後に, 光軸 (つまり, c 軸) が YZ 平面にあり, y 軸と \phi の角度をなす縦異方性を考慮すると, 対角成分 \epsilonxx, \epsilonyy, \epsilonzz, および非対角成分 \epsilonyz と \epsilonzy はゼロ以外ですが, 残りの成分はゼロです. 相対誘電率テンソルは, 以下に示すように回転行列 [R] を使用して評価できます. ここで, 回転行列 [R] は, YZ 平面で c 軸を回転させるためのものです. \epsilonyy は異常屈折率 (~2.19) の2乗です. これは, c 軸が主 y 軸に沿っているためです. 一方, \epsilonxx, \epsilonzz は常屈折率 (~2.31) の2乗です. 非対角要素 \epsilonyz と \epsilonzy は, 以下に示すように, 行列の乗算から導出されます.
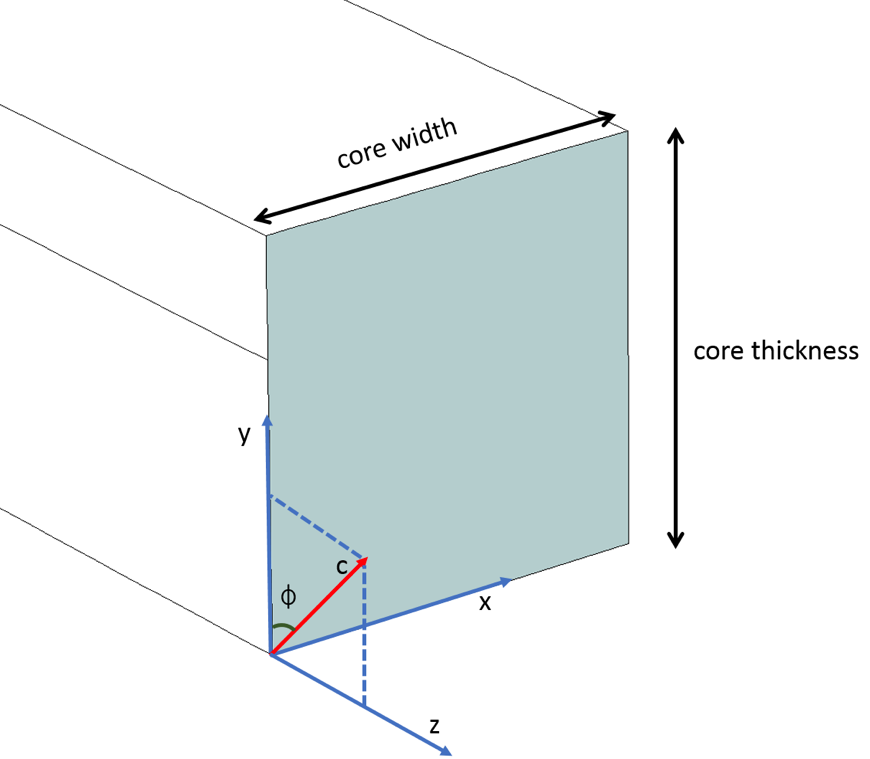
c 軸は YZ 平面にあり, x 軸と \phi の角度をなしています.
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & -sin(\phi)\\
0 & sin(\phi) & cos(\phi) \\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz} \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & sin(\phi)\\
0 & -sin(\phi) & cos(\phi) \\
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & (\epsilon_{yy}) cos^2(\phi) + (\epsilon_{zz}) sin^2(\phi) & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}) sin(\phi)cos(\phi)\\
0 & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}) sin(\phi)cos(\phi) & (\epsilon_{zz}) cos^2(\phi) + (\epsilon_{yy}) sin^2(\phi)\\
\end{bmatrix}
相対誘電率テンソル ε は, YZ 平面で角度 \phi で回転する回転行列とともに扱われます.
次に, 導波管の長さを 0.5 um から 4 um までパラメトリックにスイープして, 次の図に示すように, 縦方向異方性コアの分散曲線を導出するモード解析を実行します. この場合, \phi = 45° (つまり, c 軸は YZ 平面にあり, y 軸と 45° をなします) (参考文献3).
縦方向異方性コアを持つ分散曲線.
異方性材料のモデリングに関する最終的な考察
このブログでは, COMSOL Multiphysics のモード解析を使用して, 異方性光導波路の定性的解析 (伝搬モード) と定量的解析 (分散曲線) を実行しました. 対角異方性, および非対角の横方向異方性および縦方向異方性を考慮して, 分散関係を導き出しました. これらのタイプの解析により, 材料および形状パラメータの最適化を実行する際の柔軟性が向上し, 異方性材料の物理特性を詳細かつ直感的に理解できるようになります.
開始するのに役立つ簡単なチュートリアルモデルは, 3D光ファイバーの2D断面のモード解析を含む ステップインデックスファイバーです.
次のステップ
これらのモデルを試すには, 下のボタンをクリックしてください.
シリコンフォトニクスシリーズのブログの更新リスト
参考文献
- E. Hecht, Optics, Pearson.
- E.A.J. Marcatili, “Dielectric rectangular waveguide and directional coupler for integrated optics”, Bell Syst. Tech. J., vol. 48, pp. 2071–2102, 1969.
- M. Koshiba, K. Hayata, and M. Suzuki, “Finite-element solution of anisotropic waveguides with arbitrary tensor permittivity,” Journal of Lightwave Technology, vol. 4, no. 2, pp. 121–126, 1986.








コメント (0)