自然対流は, 電子機器の冷却, 室内気候システム, 環境輸送問題など, 多くの科学および工学アプリケーションで見られる現象です. COMSOL Multiphysics® ソフトウェアのバージョン 5.2a の CFD および熱伝達モジュールには, 自然対流問題の設定と解決を容易にする機能が含まれています. このブログでは, 自然対流の概要, 新機能, および自然対流をモデル化する際に遭遇する可能性のあるいくつかの問題について説明します.
自然対流とは?
自然対流は, 流体の浮力によって引き起こされる輸送の一種です. この浮力は, 温度または組成による流体の密度の変化によって生じます.
室内気候システムにおける自然対流の概念はご存知かもしれません. このシナリオでは, 熱源に近い天井に熱い空気が上昇し, 冬の窓などの冷たい表面に近い床に冷たい空気が沈みます.
電子機器の冷却は, 機能するために自然対流に依存することが多い別のタイプのプロセスです. たとえば, ホームシネマシステムのアンプやテレビを冷却するために, 騒音の大きいファンを使用したくはありません. 静かな環境で動作する必要がある電子機器は, 内蔵ヒートシンク上で空気を循環させるために自然対流に依存することがよくあります.
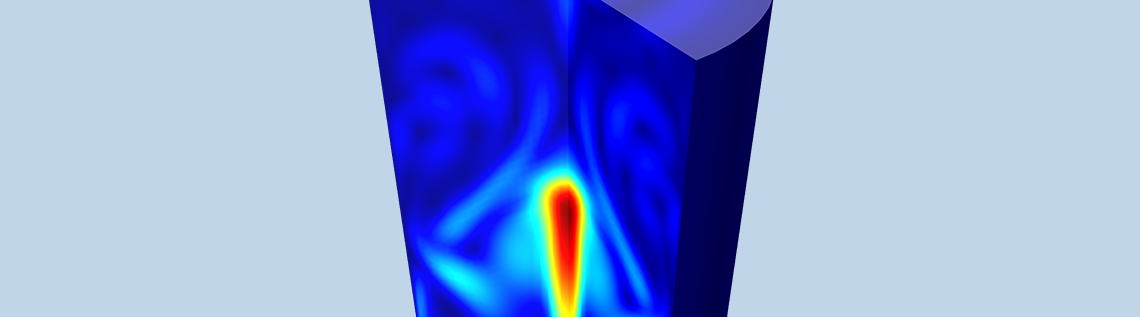
下から加熱される広がったピンフィンヒートシンクの周りの自由対流. アニメーションは, ヒートシンク周辺の空気の速度の値を示しています.
あまり目立たない自然対流の問題は, 化学や食品加工などの業界で見られます. 環境科学や気象学にも自然対流の問題が関係しており, 科学者やエンジニアは空気や水の輸送を予測して理解しようとしています.
上記のすべてのケースにおいて, エンジニアや科学者が自然対流を制御するシステムを理解して設計することが重要です. この文脈では, 数学的モデリングが最適なツールです. COMSOL Multiphysics® の最新バージョンでは, 自然対流に関する問題の定義と求解がさらに容易になっています. この目的のために, いくつかの新機能を導入しました.
流体流れインターフェースの弱圧縮性流オプションは, 自然対流ではほとんど重要でない圧力波の影響を無視します. これにより, 自然対流の問題に対して, より大きな時間ステップとより短い解析時間が可能になります.
浮力駆動流のブシネスク近似を備えた非圧縮性流オプションは, 熱膨張係数を使用して密度を線形化します. このオプションでは, 運動量方程式の体積力としてのみ密度の変化が含まれます. これは, 弱圧縮性流オプションと比較してさらに大きな簡略化を意味しますが, それでも密度の変化が小さい系に対しては優れた効率的な記述を提供します. この簡略化は, 温度差が小さい水中の自由対流に対してほぼ常に有効です.
重力機能を使用すると, 静水圧の参照点を簡単に定義でき, 垂直境界での静水圧の変化も自動的に考慮されます.
これらの新機能の詳細と, 自然対流モデリングの問題にどのように適用できるかを学びましょう.
弱圧縮性流による自然対流問題の求解
非等温流れインターフェースには, 圧力に関する密度の変化を無視することで流れの問題を簡略化する弱圧縮性流オプションが含まれています. このオプションでは, 求解に密なメッシュと小さな時間ステップが必要な圧力波の記述も排除されるため, 計算時間も比較的長くなります. 自然対流では, 通常, 圧力波の影響はほとんどありません. つまり, この単純化を行っても, モデルによる現実の記述の忠実度はほとんど失われません.
圧縮性流体の連続方程式は次のようになります:
(1)
ここで, ρ は密度, u は速度ベクトルです.
気体の場合, 密度は圧力と温度に比例します. たとえば, 理想気体の場合, 次の式が得られます:
(2)
密度変化の動的影響を無視すると, 次の式が得られます:
(3)
理想気体の密度の式を使用し, 圧力が密度に与える影響を無視すると, 次の連続方程式が得られます:
(4)
これは, 密度の変化が温度の変化に関してのみ考慮されることを意味します. 密度の変化により流体が膨張する可能性がありますが, 弱圧縮性流設定を使用する場合, それらの膨張による圧力場への直接的な動的影響は無視されます.
連続方程式の密度表現に加えて, 流体流れインターフェースの設定で重力チェックボックスを選択すると, 運動量方程式に重力方向の体積力が追加されます. デフォルトでは, これは負の z 方向です. この力は次のようになります:
(5)
ここで, 密度 ρ は温度の関数です.
理想気体の場合, 密度は温度に反比例します.
弱圧縮性流オプションの設定は, 非等温流れインターフェースまたは共役伝熱インターフェースを選択すると見つかります. モデルビルダーで流体流れインターフェースノードを選択すると, 以下の設定ウィンドウが表示されます. 弱圧縮性流オプションを選択すると, 圧力と密度間の依存関係がなくなり, 重力を選択すると, 運動量方程式に浮力の体積力が自動的に追加されます.
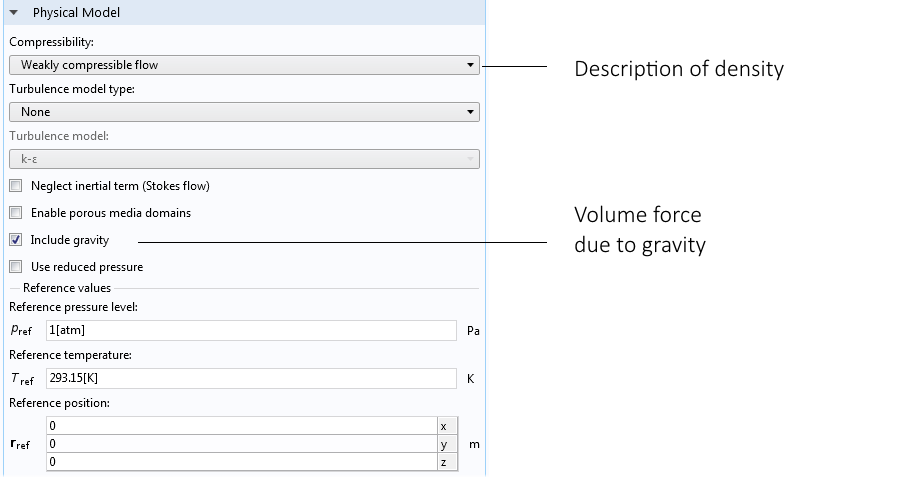
流体流れインターフェースの設定ウィンドウには, 弱圧縮性流オプションと重力機能が表示されています.
下の図は, 垂直に配置された2つの回路基板間の流れを示しています. 図には, 1つの回路基板のユニットセルのみが表示されています. 2つ目の回路基板は, 背面が見える基板に面するように, すぐ前に置かれています. 流れは完全に浮力によって駆動されます. つまり, ファンはありません.
入口での流量は約 0.2 m/s, 出口では約 0.3 m/s です. 側面からの空気の流入はありません. つまり, 流量の違いは, 回路基板間のチャネルの高さに沿った温度の上昇によって生じる膨張によるものです.
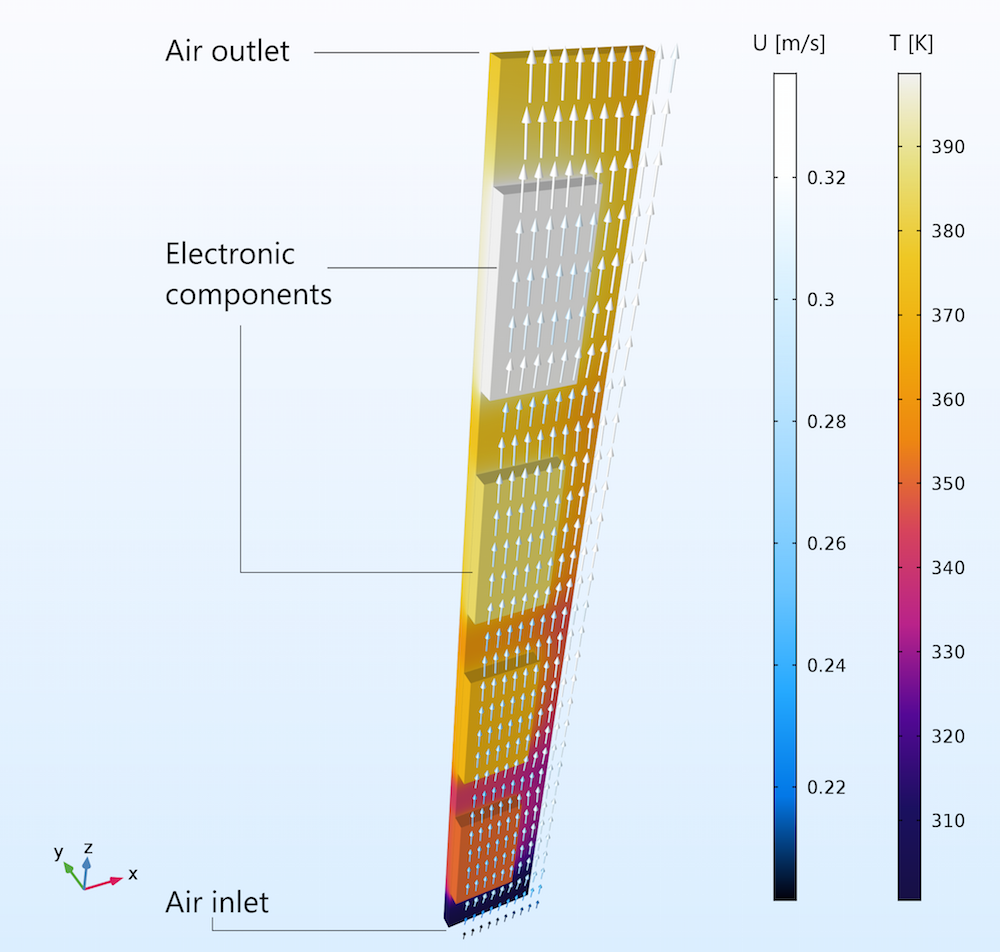
垂直回路基板間の浮力駆動流れ. 膨張は矢印の色の凡例に表示されており, 流速は入口で約 0.2 m/s, 出口で約 0.3 m/s です.
ブシネスク近似による非圧縮性流
膨張が速度場に与える影響に関して密度の変化が無視できる場合は, 自然対流にブシネスク近似 とともに非圧縮性流オプションを使用できます. これは, 流体を非圧縮性として扱うことで, 連続方程式が弱圧縮性流オプションよりもさらに簡略化されることを意味します. この場合, 連続方程式は次のようになります:
(6)
代わりに, 密度の小さな変化は体積力で考慮され, 体積力は重力の反対方向, デフォルトでは z 方向の運動量方程式に導入されます. 密度の小さな変化は, 基準温度での流体の密度を線形化することによって得られます. 体積力の z 成分は次のようになります:
(7)
ここで, g は重力定数, \[{\rho _{{\text{ref}}}}\] は特定の基準温度での密度, α は流体の熱膨張係数, ΔT は基準温度に対して測定された温度差です.
浮力駆動流にブシネスク近似を使用する利点は, 流体流方程式の非線形性が低減され, 問題を数値的に解くのが容易になり, 反復回数が少なくなり, 時間依存の問題に対してより大きな時間ステップが可能になることです.
ブシネスク近似が流れを現実的に記述できる典型的な例は, 比較的小さな温度差にさらされた液体の水をモデル化する場合です. 下の図は, 下から加熱されたコップに入った水の自然対流を示しています. ここでは, コップの中央と底部付近で上向きの流れがあり, 垂直壁と中央の間で下向きの流れがある, 非常に複雑な流れパターンが得られます.
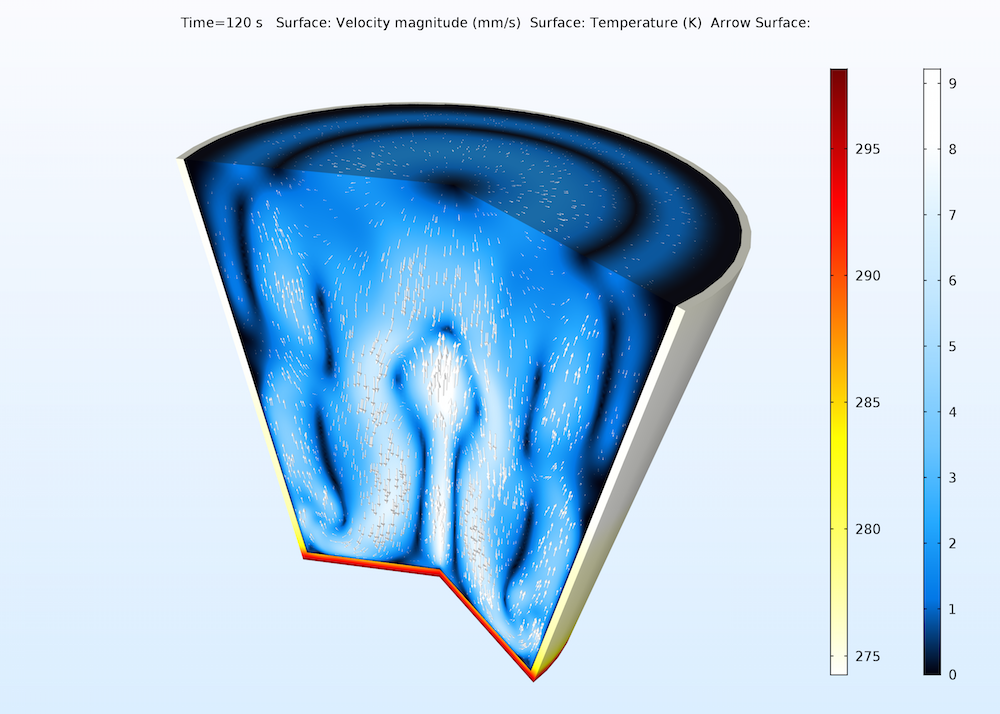
コップ一杯の水の自然対流. このプロットは, コップ内の速度場とコップの壁の温度分布を示しています.
COMSOL Multiphysics® の流体流れインターフェースで, 下図に示す設定を選択すると, 浮力駆動流れのブシネスク近似による非圧縮性流オプションを取得できます.
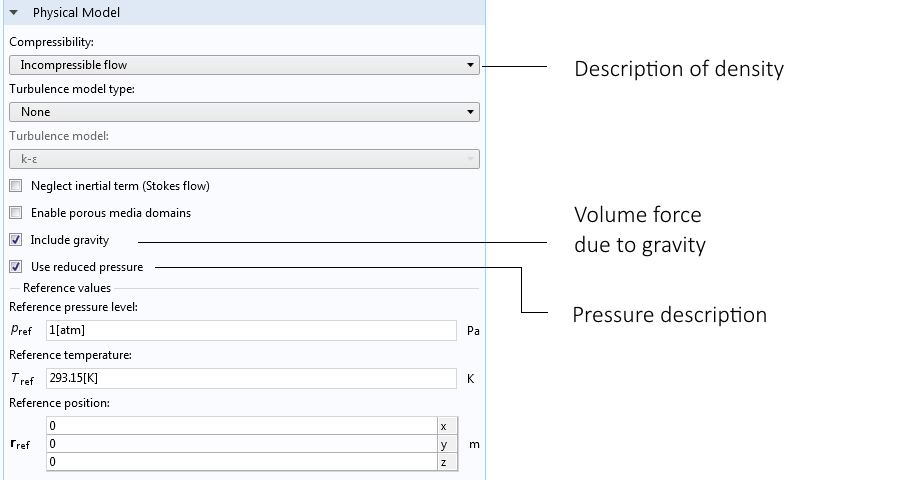
非圧縮性流オプション, 重力機能, および減圧を選択すると, 自然対流問題に対するブシネスク近似が得られます.
自然対流モデルにおける圧力方程式の制約
完全に圧縮可能な流れをモデル化する場合, 密度は圧縮性流体の圧力の関数であるため, 圧力の時間依存性が連続方程式に含まれます. これは, 境界で圧力を指定しない場合でも, 通常は圧力の初期条件を含めるだけで, 適切に設定された問題が得られることを意味します.
弱圧縮性および非圧縮性の流れの場合, 上記の説明に従って, 連続方程式の時間依存圧力項は無視されます. 圧力を設定する境界条件がない場合, 圧力場は, ドメイン内のどこかの点で設定しない限り, 不確定になります.
COMSOL Multiphysics® では, 不確定な圧力場を回避するために, いわゆる圧力ポイント拘束を使用できます. 基準圧力点がないと, 自然対流問題を解くときに収束の問題が発生することがよくあります.
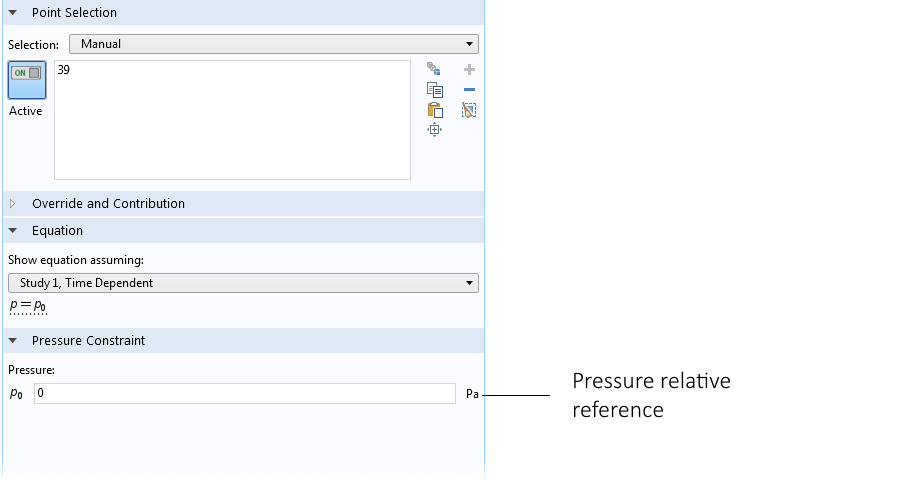
水ガラスの例における圧力ポイント拘束の設定.
連成/非連成による自然対流問題の求解
自然対流を記述する方程式には通常, 運動量方程式, 連続方程式, エネルギー輸送または質量輸送方程式が含まれます. 浮力が温度差によって駆動される場合, エネルギー方程式は流体流れ方程式 (ナビエ・ストークス方程式) と完全に連成されます. 自然対流の場合, この連成はかなり緊密です. つまり, 方程式を解く最も堅牢な方法は, COMSOL Multiphysics® の完全連成ソルバーを使用することです.
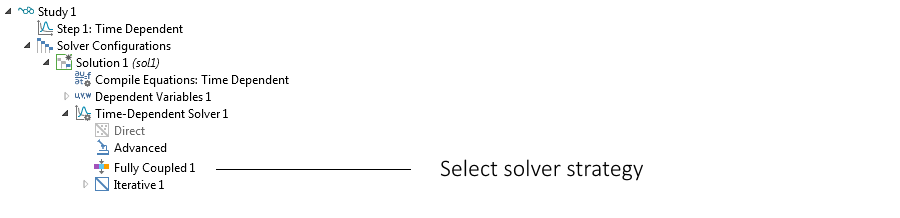
完全連成ソルバーオプションが設定されたモデルツリーのソルバーブランチ.
非常に大きな問題の場合, 分離アプローチが望ましい選択肢となる場合があります. たとえば, 化学種が多く, 浮力が化学組成による密度の変化によって引き起こされる場合, 分離アプローチは, 求解プロセスで適切なメモリ消費量を得るための唯一の実行可能な選択肢となる可能性があります.
おわりに
このブログをもう1つ自然対流の問題で締めくくりたいと思います. 私はよく葉巻を吸うときの自然対流について考えます. 喫煙を推奨するつもりはありませんが, 私のお気に入りの自然対流の問題は, 寒い冬の日に葉巻から出る煙です. 下の図は, 灰皿の上に置かれた火のついた葉巻と, 燃焼熱によって生じた流れの分布を示しています.
灰皿に置かれた火のついた葉巻の周りの自然対流 (小さな強制成分を含む).
火のついた葉巻によって引き起こされる流れの一部は, 実際には強制対流です. タバコの大部分が煙になり, 密度が約 500 ~ 1000 kg/m3 から 1 kg/m3 に変化するためです. これは, 灰と葉巻の周囲の空気の境界にある流れの入口と言えます.
その他の資料
- COMSOL ブログで自然対流と流体流れのモデリングについてさらに学ぶ:






コメント (0)