
半導体モジュールでは, COMSOL Multiphysics® ソフトウェアのバージョン 5.6 以降, シュレーディンガー方程式フィジックスインターフェースの機能が単一成分から多成分の波動関数に拡張されました. これにより, スピンを持つ粒子や 3 つの p 型軌道が混在する価電子帯構造など, より広範囲の系のシミュレーションが可能になります. このブログでは, シンプルなベンチマークモデルを使用して, この多成分波動関数機能の使用方法を説明します.
ハミルトン行列
波動関数が複数の成分を持つ場合, ハミルトニアンは波動関数の成分のベクトルに作用する行列となります. 例えば, 時間依存シュレーディンガー方程式は次のように表されます.
(1)
ここで, N は波動関数成分の個数を表します.
時間発展演算子の式の右側にあるマイナス記号は, COMSOL Multiphysics® のすべてのフィジックスインターフェースが, exp(i k x – i \omega t) という物理符号規則ではなく, exp(-i k x + i \omega t) という工学符号規則を採用しているためです. 後で, 運動量演算子の符号も, このためほとんどの教科書で見られるものと異なることがわかります.
一般に, ハミルトン行列\mathbf{H}_{mn}の各要素には, 0, 1, または2つの偏微分項が複数含まれることがあります:
(2)
\frac{+\hbar^2}{2\,m_e} \sum_{ i,j\in \{1,2,3\}} \left[
\frac{i\, \partial}{\partial r_i} \,A_{ij}^{mn}(\mathbf{r}) \, \frac{i\, \partial}{\partial r_j}
+ \frac{i\, \partial}{\partial r_i} \,H_i^{mn(1R)}(\mathbf{r})
+ H_j^{mn(1L)}(\mathbf{r}) \, \frac{i\, \partial}{\partial r_j}
+ H^{mn(0)}(\mathbf{r})
\right]
ここで, m_e は電子の質量; \mathbf{r} は位置ベクトル \mathbf{r}=\{r_1,r_2,r_3\}\equiv\{x,y,z\}; A, H^{(1R)}, H^{(1L)}, H^{(0)} は空間的に変化する可能性のある係数です.
最初の項では, 左側の微分演算子は係数 A と波動関数成分 \psi_{n} の両方に作用すると理解します. 同様に, 2 番目の項の微分演算子は H^{(1R)} と \psi_{n} の両方に作用します. 前述のように, すべての運動量演算子は通常の慣例とはマイナス符号が異なることに注意してください.
ハミルトン行列の要素数は, 波動関数の成分数の 2 乗に比例して増加します. 各要素には, 式 2 に示すように, さまざまな次数の偏微分項が含まれる場合があります. 限られたウィンドウサイズ内でこれらの項をグラフィカルユーザーインターフェースに柔軟かつ効率的に入力できるように, バージョン 5.6 以降ではいくつかの組み込み機能を作成しました. 以下のサンプル モデルでは, これらの機能の使用方法を示します.
モデル系
前述のように, ハミルトン行列要素のすべての係数は空間的に変化する可能性があります. これは, 量子細線や量子ドットなどのヘテロ構造やナノ構造に特に当てはまります. 簡単にするために, すべての係数が空間的に均一である, 均一に歪んだバルク結晶のモデルを選択しました. ただし, この単純なモデルは, ハミルトン行列要素をユーザーインターフェースに入力する手順を説明するという目的には役立ちます. さらに, この単純な系の解析解を使用して数値解を検証するためのベンチマークモデルとしても機能します.
窒化ガリウム(GaN)は, オプトエレクトロニクス, 高出力, 高周波用途の重要なワイドバンドギャップ半導体材料です. ChuangとChangは, 1996年にGaNを含むウルツ鉱型結晶の6×6ハミルトン行列の導出と計算を発表しました(文献 1). 論文の式45では, 6×6ハミルトン行列がブロック対角化されており, 左上の3×3行列は次のようになります.
(3)
F & K_t & -i H_t \\
K_t & G & \Delta-i H_t \\
i H_t & \Delta+i H_t & \lambda
\end{array}\right]
行列要素は文献1の式(34)と式(42)で与えられます. 例えば, 3行3列のハミルトン行列の(1,1)の位置にある要素は
(4)
最初の2つの項は数値であり, 他の2つには演算子と数値が含まれています:
(5)
(6)
論文の図 5 に示されている結果と比較するために, 結晶運動量 k_y の y 成分をゼロに設定します. シュレーディンガー方程式 インターフェースでは, 他の 2 つの成分 k_x と k_z は, それぞれ偏微分 i\partial / \partial x と i\partial / \partial z に置き換えられます (脚注を参照). 従って, 上の2つの方程式は次のようになります.
(7)
i\frac{\partial}{\partial z} A_1 i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} A_2 i\frac{\partial}{\partial x}
\right]+\lambda_\epsilon
(8)
i\frac{\partial}{\partial z} A_3 i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} A_4 i\frac{\partial}{\partial x}
\right]+\theta_\epsilon
最後に, ひずみから来る数は
(9)
(10)
となります. ここで, \epsilon はひずみ成分です.
エネルギーパラメーター \Delta_1 と \Delta_2, 有効質量パラメーター A_1~A_1, および変形ポテンシャル D_1~D_1 は, 文献 1 の表 III に記載されています.
式 4 を 3 行 3 列のハミルトン行列の (1,1) 位置の要素 F について展開し, 式 7 と 式 8 を用いると, 次の式が得られます.
(11)
\frac{\hbar^2}{2m_e}\left[
i\frac{\partial}{\partial z} (A_1+A_3) i\frac{\partial}{\partial z}
+ i\frac{\partial}{\partial x} (A_2+A_4) i\frac{\partial}{\partial x}
\right]
+\Delta_1+\Delta_2
+\lambda_\epsilon
+\theta_\epsilon
最初の項には演算子が集められており, 他の4つの項は数値です.
数値的および解析的方法
Ref. 1 の図 5 では, k_x および k_z 方向に沿った価電子帯分散が, k_y をゼロに設定して, 歪んでいない結晶と歪んだ結晶についてプロットされています. 検討中の系はバルク結晶であるため, k_x と k_z は単なる数値であり, ハミルトニアン (3) は, k_x と k_z の指定された値に対応する特定の数値の 3×3 行列に縮約されます. この行列の固有値を数値的に計算すると, 図に示すバンド構造が得られます. これは本論文で採用されている分析的アプローチであり, 次に議論される数値的アプローチを検証するために使用されます.
量子井戸や量子ドットなどの一般的な不均一構造では, 前述のように, 数値 k_x と k_z を偏微分 i\partial / \partial x と i\partial / \partial z に置き換え, xz 平面上のシュレーディンガー方程式を解いてバンド構造を取得します. これが数値アプローチです. もちろん, バルク結晶の単純な系ではこれはやりすぎになります. しかし, 教育と検証の目的で, この単純な系を選択しました. 物理特性を使用してこの単純なモデルを構築する方法を習得すると, 数値アプローチでのみ求解できるより複雑な系をシミュレートできるようになります.
COMSOL マルチフィジックスモデル
ハミルトニアンのサイズは 3×3 なので, モデルウィザードまたはフィジックスインターフェースの 設定 ウィンドウのいずれかで波動関数の成分数を 3 に設定するのは簡単です.
上で説明したように, モデルは x 方向と z 方向の 2D です. モデル表記を読みやすくするために, 下のスクリーンショットに示すように, 2 番目の軸の座標名をデフォルトの y から z に変更します.
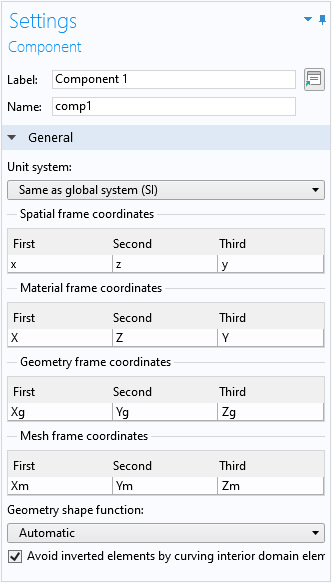
関心のある方向(xとz)に合わせて座標名を変更します.
ゾーン中心付近のバンド構造のみに関心があるため, 単位セルよりわずかに小さい単純な正方形領域を使用し, シュレーディンガー方程式にフロケ・ブロッホ周期境界条件を使用できます. この領域では, 問題は均一な連続体に近づき, 少数のメッシュ要素で十分です. (同じ手法を使用した機械モデルについては, 薄膜 BAW 構造のチュートリアルモデルを参照してください. )
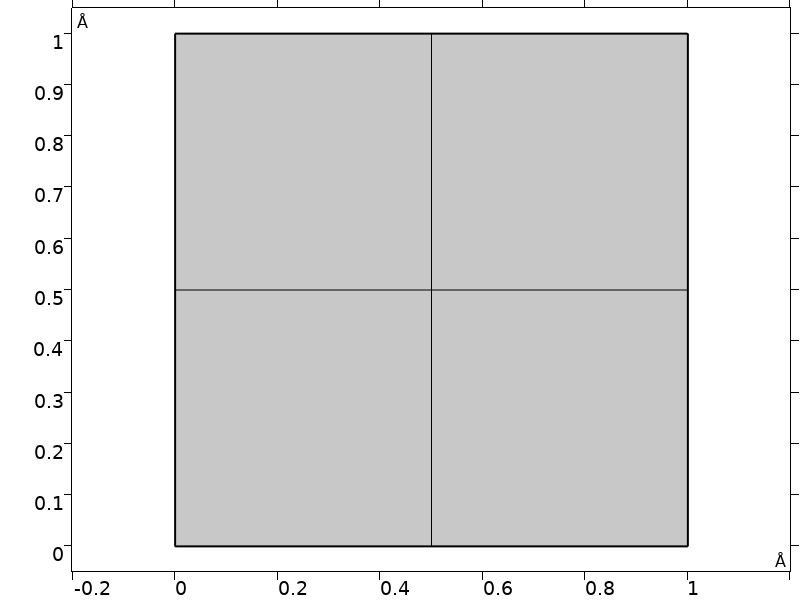
モデルのドメインとメッシュ.
論文の図 5 と比較するためのプロットを簡単に作成するために, 正の軸が kx 軸を表し, 負の軸が kz 軸を表すようにスイープパラメーター kp を設定しました. これを実現するには, 以下のスクリーンショットに示すように, パラメーター kx と kz の式で if ステートメントを使用します.
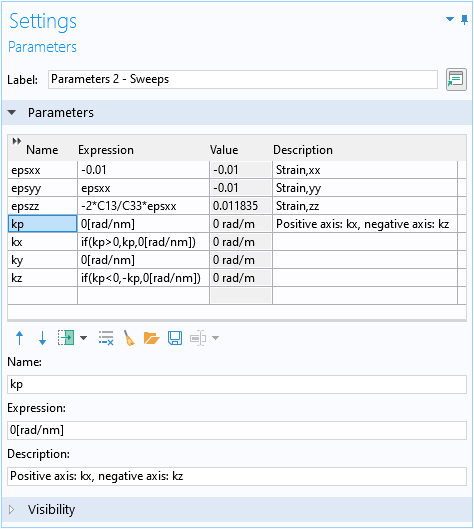
kx と kz の 2 軸 1D プロットのパラメーター kp を設定します.
解析解
解析的アプローチでは, 式 3 で示される 3×3 エルミート行列を対角化するグローバル方程式を設定します. グローバル方程式の固有値には予約名 lambda を使用します. ハミルトニアンは 1 meV のエネルギースケールでスケーリングし, ソース項がほぼ 1 のオーダーになるようにします. 固有エネルギーは meV 単位の固有値です. また, 行列の列を揃えるために式に空白をいくつか追加します.
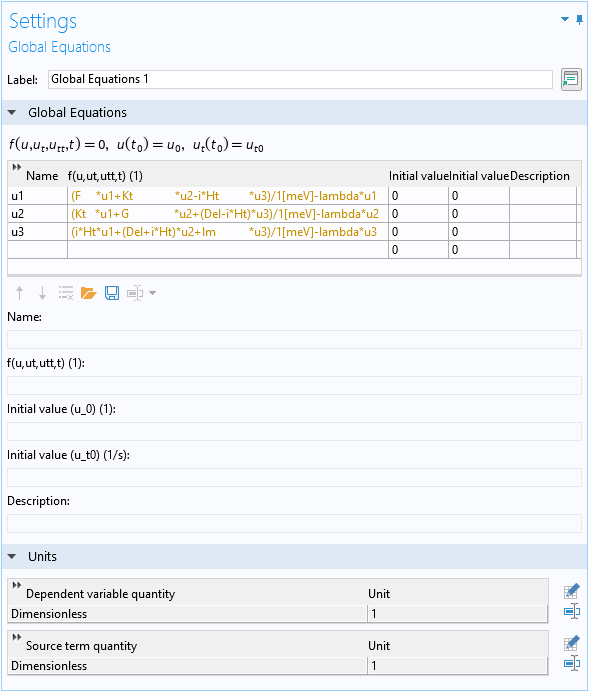
3×3 の固有値を見つけるためのグローバル方程式.
この時点では固有値変数 lambda がまだ定義されていないため, テキストは黄色になっています.
シュレディンガー方程式を解く
前述のように, 数値的アプローチではシュレーディンガー方程式を解きます. 論文の図 5 と比較するためのプロットを便利に作成するために, 固有値スケールを図の縦軸と同じエネルギー単位 (meV) に設定し, 固有値が同じ単位 (meV) の固有エネルギーの数値をとるようにします.
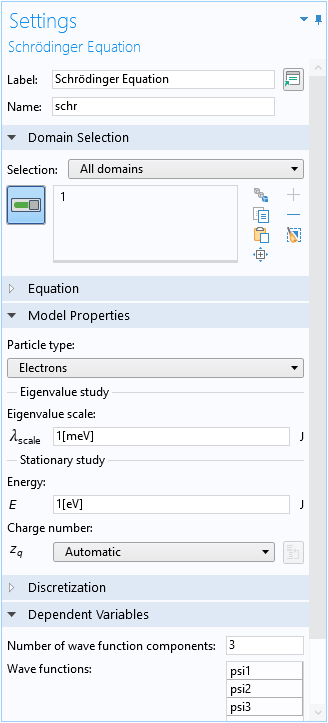
シュレーディンガー方程式フィジックスインターフェースの設定ウィンドウ.
ハミルトン行列入力
これで, 3×3 ハミルトニアンの行列要素を入力する準備ができました. ここでも, (1,1) 位置の要素 F を例として使用します. この要素への寄与は, 式 11 にまとめられています. 最初の項には 2 次導関数が含まれているため, 2 次ハミルトニアン ドメイン条件を追加します. この機能は, シュレーディンガー方程式 フィジックスインターフェースの複数成分波動関数を処理する機能とともに, COMSOL Multiphysics® 5.6 で導入されました.
このドメイン条件の 設定 ウィンドウの中心的な機能は, ハミルトン入力テーブルです. このテーブルの最初の2列は, 入力するハミルトン行列要素の行インデックスと列インデックス用です. 各インデックスはドロップダウンメニューから選択され, 1 から N (波動関数の成分数) まで自動的に入力されます. たとえば, ここでは N を 3 に設定しているので, ドロップダウンメニューには 1, 2, または 3 の選択肢があります. テーブルにデータを入力する前に, 必ず波動関数の成分数を決定して設定してください (以下の 既知の制限 セクションを参照してください).
3列目と5列目は, 2つの微分演算子用です. これらは, モデルの空間次元に応じて微分演算子が自動的に入力されるドロップダウンメニューとしても提供されます. ここでは, xz 平面に2Dモデルを設定しているため, 選択肢は i\partial / \partial x と i\partial / \partial z です.
4列目は有効質量パラメーター A 用です. COMSOL Multiphysics® のほぼすべての他の入力フィールドと同様に, 入力フィールドは数値, パラメーター, 変数, またはその他の数式を受け入れます. このタイプのドメイン条件には, 現在の条件, 1次ハミルトニアン, 左, 1次ハミルトニアン, 右, 0次ハミルトニアン など, 常に \hbar^2/2m_e の前因子が組み込まれています.
最後の列 説明 では, 入力テーブルの各エントリを文書化できます. ハミルトン行列の各要素, たとえば 式 11 で示される要素 F には, さまざまな種類の項が含まれており, 複数の異なる機能にわたって複数のテーブル行に入力されます. そのため, 説明 列に適切なコメントを入力して, 各テーブル行を追跡することが重要です.
以下のスクリーンショットは, ドメイン条件の 設定 ウィンドウを示しています. ここでは, 式 11 の最初の項が ハミルトニアン入力テーブル の最初の2行に入力されています. 行列要素 F の位置は (1,1) なので, 行インデックスと列インデックスは両方とも1です. テーブル内の2行の微分演算子と A パラメータは, 式 11 の角括弧内の2つの項に対応しています. 説明 列には, 寄与元が記録されます. この場合, 2行は元々 式 4 の F=\lambda+\theta 部分から取得されています.
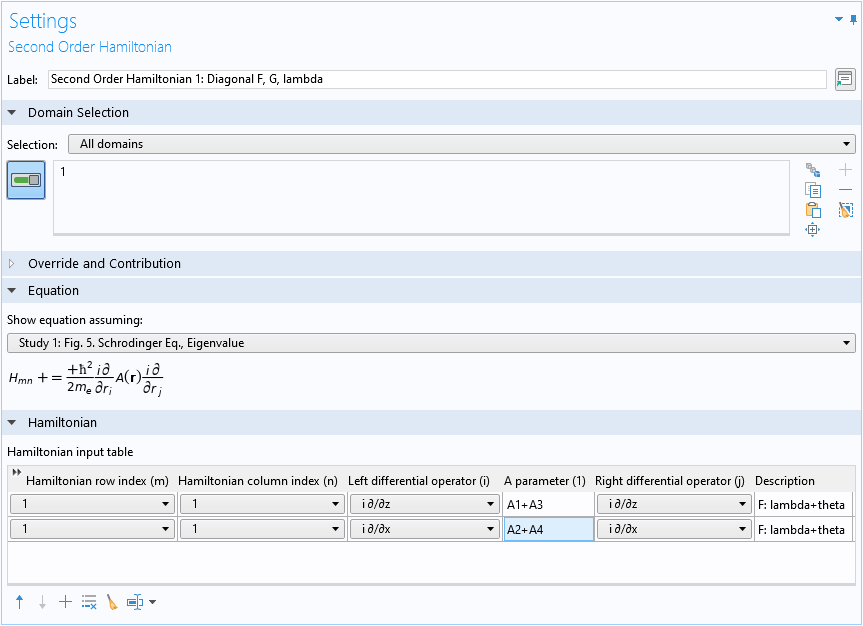
2次ハミルトニアンドメイン条件の設定ウィンドウ. 行列要素Fの最初の項が入力されています.
表の行をコピー/ペースト
(1,1) 要素 F の残りの項を入力する前に, (2,2) 要素 G の2次演算子部分が F のものと同じであることに気付きます. 文献 1 の式 34 から:
(12)
であり, したがって, 2 次ハミルトニアン (G=\lambda+\theta) への寄与は同じになりますが, 位置が異なります. つまり, (1,1) ではなく, (2,2) になります.
G の2行のデータを最初から入力する代わりに, F の2行をコピーして貼り付け, 行と列のインデックスを 2 に変更します. まず, マウスをクリックしてドラッグし, 表の2行を選択します:
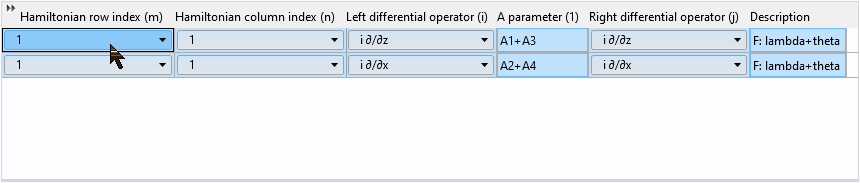
次に右クリックして選択した行をコピーします:
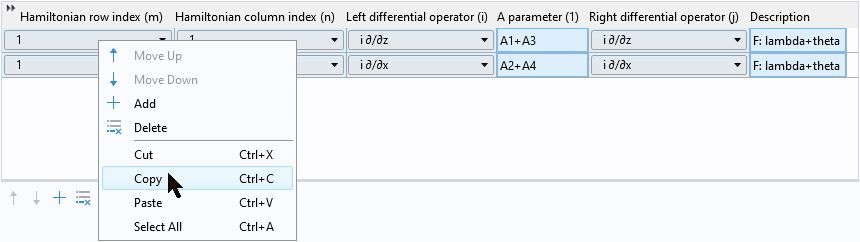
次に, 追加ボタンをクリックして新しい行を追加します:
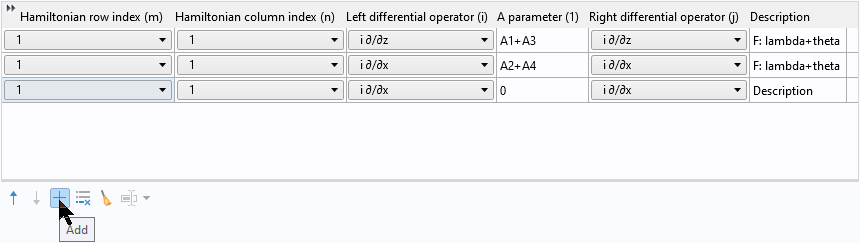
次に, 右クリックしてコピーした2行をテーブルに貼り付けます:
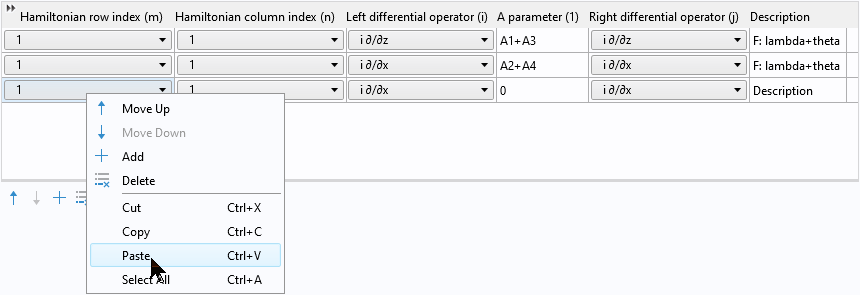
貼り付けた後, 同じ行が2組あります:
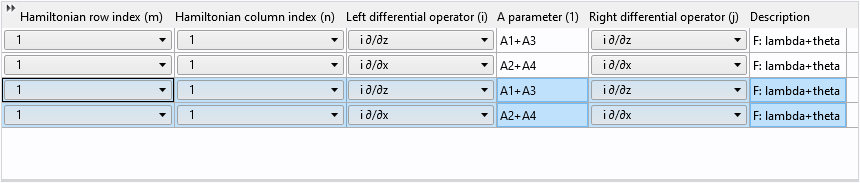
最後に, 行と列のインデックスを1から2に変更し, 説明を更新します:
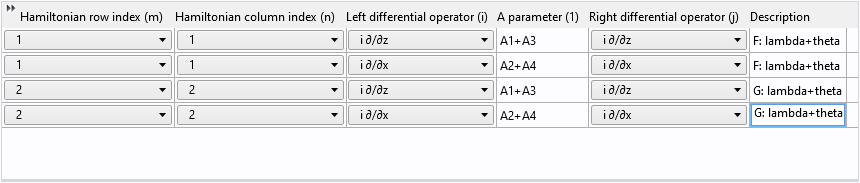
このようにテーブル行を再利用すると, 時間が節約されるだけでなく, 間違いを防ぐのにも役立ちます.
デフォルトの有効質量寄与を無効にする
対角要素について先ほど示した 2次ハミルトニアン ドメイン条件は, デフォルトの 有効質量 機能によって通常追加される運動エネルギー項に対応します. ハミルトニアンへの不要なデフォルトの寄与を除去するには, これを無効にする必要があります.
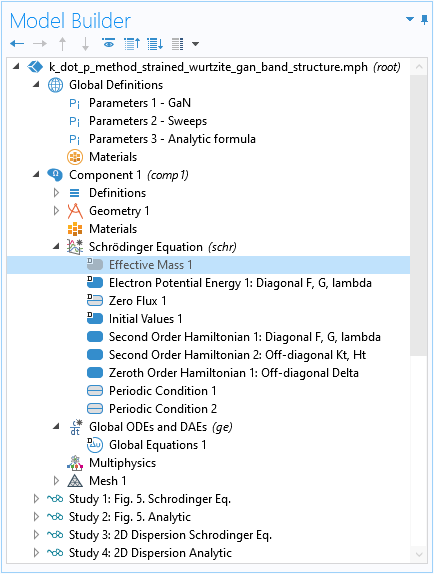
デフォルトの有効質量機能を無効にして, ハミルトニアンへの不要な寄与を削除します.
演算子のない項
(1,1) 要素 F (式 11 の最後の4つの項: \Delta_1+\Delta_2+\lambda_\epsilon+\theta_\epsilon) の残りの項 (単なる数値) を入力するには, 要素がハミルトン行列の対角線上にあるため, 以下のスクリーンショットに示すように, ゼロ次ハミルトニアン ドメイン条件, またはデフォルトの 電子ポテンシャルエネルギー ドメイン条件のいずれかを使用できます.
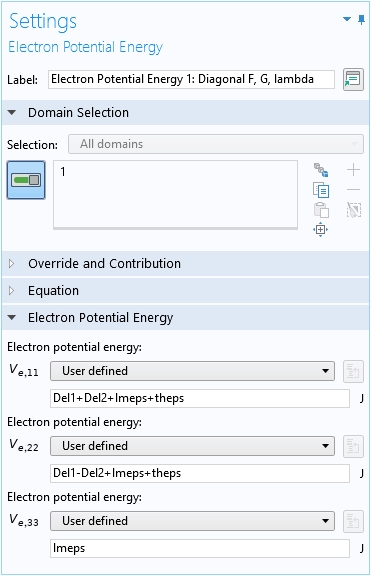
ハミルトン行列の対角要素のゼロ次項には, デフォルトの電子ポテンシャルエネルギー領域条件を使用します.
非対角要素
非対角要素については, 同じ手順で2次項のハミルトニアン入力テーブルを埋めていきます:

そしてゼロ次の項:

前述のように, 0次ハミルトニアンには \hbar^2/2m_e の前因子が組み込まれています. したがって, 入力量 (この場合は Del) がエネルギー単位である場合は, 前因子で割る必要があります.
既知の制限
ハミルトン行列入力テーブルにデータが入力された後に波動関数の成分数が変更されると, テーブル行が同期されなくなります. この時点で, テーブルをクリアして, 再度データを入力する必要があります. ハミルトン入力テーブルにデータを入力する前に, まずモデルで解析する特定のハミルトン行列を決定し, それに応じて波動関数の成分数を入力することをお勧めします.
他の設定
Floquet-Bloch 周期境界条件を設定して単純なマップメッシュを作成し, 固有値研究で特別に用意されたパラメーター kp を使用して波数ベクトルのスイープを構成するのは簡単です.
グローバル方程式で構成された解析的な 3×3 行列方程式を解くには, すべての固有値オプションを使用して, 3×3 行列方程式の 3 つの固有値すべてを取得します.
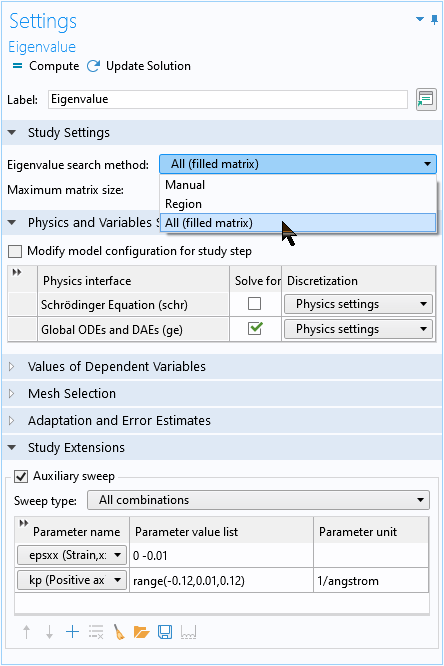
グローバル方程式の3つの固有値すべてを取得するには, すべての固有値オプションを使用します.
歪みのないウルツ鉱型結晶と歪みのあるウルツ鉱型結晶の計算されたバンド構造
以下の2つの図は, 正の kx 軸と負の kz 軸に沿った, 計算された非歪みおよび歪みのある重い正孔 (HH), 軽い正孔 (LH), および結晶場分裂正孔 (CH) の分散を示しており, 解析解 (丸) および 文献 1 の図 5 とよく一致しています.
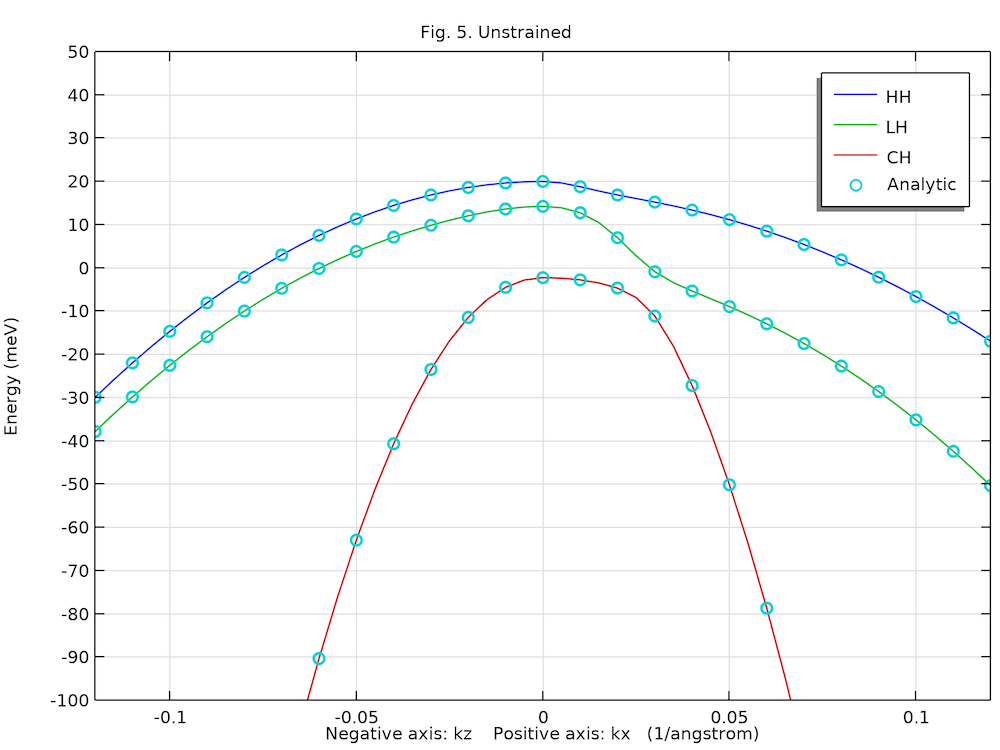
バルクGaNウルツ鉱結晶の非歪価電子帯構造.
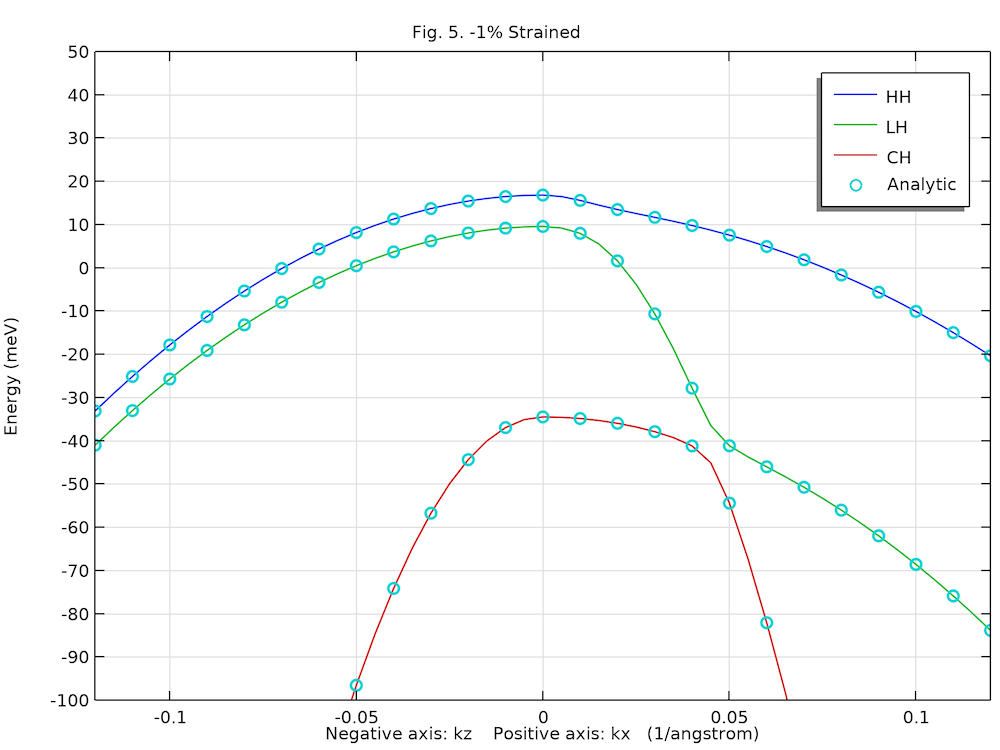
圧縮歪みを受けたバルク GaN ウルツ鉱型結晶の価電子帯構造.
以下のプロットは, 3つの価電子帯の x 方向と z 方向に沿った2D エネルギー表面を, 計算値 (カラー表面) と解析解 (灰色のワイヤーフレーム) の間で比較したものです. 一致も非常に良好です.
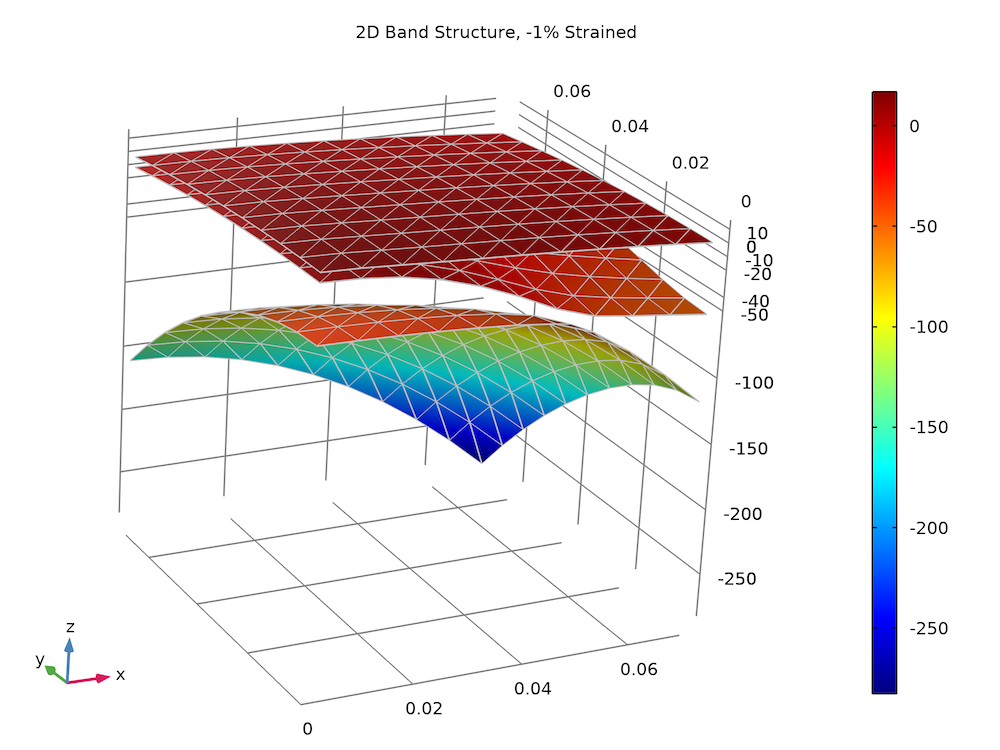
バルク GaN ウルツ鉱型結晶の歪んだ価電子帯構造.
結論
このブログでは, 単純なバルク結晶の例を使用して, 多成分波動関数を処理するための シュレーディンガー方程式 フィジックスインターフェースの新しい機能を示しました. ハミルトニアン行列は, 組み込み機能を使用してユーザーインターフェースに体系的に入力されます. 同じ方法論は, 量子井戸や量子ドットなどのより複雑な系にも適用できます. この新しい機能をシミュレーションプロジェクトにどのように使用しているか, ぜひお聞かせください.
自分で試す
下のボタンをクリックして, アプリケーションギャラリとダウンロード可能なMPHファイルにアクセスし, 歪みウルツ鉱型GaNバンド構造を自分でモデル化してみてください:
参考文献
- S.L. Chuang and C.S. Chang, “k·p method for strained wurtzite semiconductors,” Phys. Rev. B, vol. 54, p. 2491, 1996.
脚注
COMSOL® ソフトウェアの時間調和位相器の符号規則は exp(+i \omega t) であるため, 平面波は exp(+i \omega t-i k_x x) であることを思い出してください. したがって, 演算子 +i\partial / \partial x が使用され, -i\partial / \partial x は使用されません.



コメント (0)