
多相流には, 気体-液体, 液体-液体, 液体-固体, 気体-固体, 気体-液体-液体, 気体-液体-固体, または気体-液体-液体-固体の混合物の流れが含まれます. このブログシリーズでは, 主に気体-液体および液体-液体の混合物に焦点を当てていますが, 固体-気体および固体-液体の混合物についても簡単に説明します. また, CFD およびマイクロフルイディクスモジュールで使用できるモデルとモデリング手法についても確認します.
さまざまなスケールでの多相流モデリング
数学的モデリングによる多相流の研究は, いくつかのスケールで行うことができます. 最小スケールはマイクロメートルの数分の1程度ですが, 最大スケールは数メートルまたは数十メートルです. これらのスケールは約8桁に及ぶことがあり, 最大の長さスケールは最小スケールの1億倍になることがあります. これは, 最小スケールから最大スケールまでの多相流を, スケールの範囲全体にわたって同じメカニズムモデルを使用して数値的に解決することは不可能であることを意味します. このため, 多相流のモデリングは通常, 異なるスケールに分割されます.
より小さなスケールでは, 相境界の形状を詳細にモデル化できます. たとえば, 気泡と液体の間の気液界面の形状です. このようなモデルは, COMSOL® ソフトウェアでは分離多相流モデルと呼ばれます. このようなモデルを記述するために使用される方法は, 通常, 表面追跡法と呼ばれます.
より大きなスケールでは, 相境界を詳細に記述する必要がある場合, モデル方程式を解くことは不可能です. 代わりに, 異なる相の存在は体積分率などのフィールドを使用して記述され, 表面張力, 浮力, 相境界を越えた輸送などの相間効果は, いわゆる分散多相流モデルのモデル方程式でソースとシンクとして扱われます.
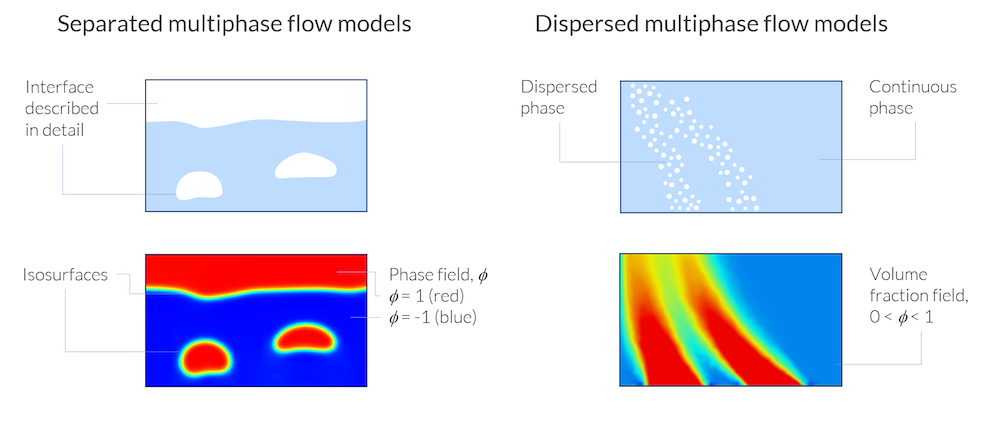
分離混相流モデルは相境界を詳細に記述しますが, 分散混相流モデルは連続相中に分散した1つの相の体積分率のみを扱います.
上の図は, 分離混相流モデルと分散混相流モデルに対する2つのアプローチの主な違いを示しています. どちらの例でも, 関数 Φ は気相と液相の存在を表すために使用されています. しかし, 分離多相流モデルでは, 異なる相は排他的であり, それらの間の相境界では, 相場関数 Φ が急激に変化します. 相場関数は, 相境界の位置を追跡すること以外に物理的な意味はありません.
分散多相流モデルでは関数 Φ は, 液体 (連続相) における気体 (分散相) の局所平均体積分率を表します. 平均体積分率は, ドメイン内のどこでも0と1の間の値をスムーズに見つけることができます. 均質化された領域に少量または大量の気泡がある場合. 言い換えれば, 分散多相流モデルでは, 気相と液相を空間と時間において同じポイントで定義できますが, 分離多相流モデルでは特定の時点と時間には, 気体か液体のいずれかが存在します.
分離多相流モデル
COMSOL Multiphysics® ソフトウェアには, 分離多相流モデル用の3つの異なる界面追跡方法があります:
- レベルセット
- フェーズフィールド
- 移動メッシュ
レベルセット法とフェーズフィールド法はどちらもフィールドベースの方法で, 相間界面はレベルセット関数またはフェーズフィールド関数の等値面として表されます. 移動メッシュ法は, 同じ問題に対するまったく異なるアプローチです. このアプローチでは, 相境界は2つのドメインを分離する幾何学的表面としてモデル化され, 対応するドメインの各側に1つの相があります.
場の問題は通常, 固定メッシュで求解されます. 移動メッシュの問題は, 当然ながら移動メッシュを使用して求解されます.
下のアニメーションは, T 字型マイクロ流路でエマルジョンが生成されるモデルの結果を示しています. このモデルでは, 問題はフェーズフィールド法で求解されます. このアニメーションでは, 相境界がメッシュの面やエッジと一致していないことがわかります. 相境界は, フェーズフィールド関数の等値面で表されます.
有限要素メッシュは, フェーズフィールド法とレベルセット法の2つの相間の相境界と一致する必要はありません.
対照的に, 下の図は, 移動メッシュを使用した上昇気泡の検証モデルを示しています. メッシュは相境界の形状に追従し, エッジはこの境界と一致します. 移動メッシュモデルの欠点も確認できます. 気泡は変形し, 2つの二次気泡が一次気泡から分離します. この時点で, 元の相境界を複数の境界に分割する必要があります. そのためのロジックは完全に単純ではなく, COMSOL® ソフトウェアにはまだ実装されていません. したがって, COMSOL® ソフトウェアの移動メッシュ法では, トポロジの変更に対応できません. フェーズフィールド法にはこの欠点がなく, 相境界の形状の変化に対応できます.
上昇気泡の検証問題. トポロジの変化は, 2つの二次バブルが一次バブルから分離するときに発生します.
フィールドベースの方法と移動メッシュの使い分け?
移動メッシュ法では, 特定のメッシュの精度が向上します. この点では, 力とフラックスを相境界に直接適用できるという利点があります. フィールドベースの方法では, この表面を定義する等値面を解決するために, 相界面の周囲に密なメッシュが必要です. 等値面を正確にたどる適応メッシュを定義することは困難であるため, 通常は等値面の周囲の大きなボリュームでメッシュを密にする必要があります. これにより, 同じ精度の場合, フィールドベースの方法のパフォーマンスは移動メッシュに比べて低下します. では, これらの異なる方法はいつ使用するのでしょうか?
- トポロジの変化が予想されないマイクロ流体システムの場合, 通常は移動メッシュ法が適しています
- トポロジの変化が予想される場合は, フィールドベースの方法を使用する必要があります:
- 表面張力の影響が大きい場合は, フェーズフィールド法が適しています
- 表面張力を無視できる場合は, レベルセット法が適しています
分離多相流モデルと乱流モデル
乱流モデルを使用する場合, 平均速度と圧力のみが解析されるため, 流れの詳細は失われます. これを念頭に置くと, 表面張力の影響も流れのマクロ的な説明にとってそれほど重要ではなくなります. 乱流は流れが表面でも比較的活発であることを意味するため, トポロジの変化を避けることはほとんど不可能です. したがって, 乱流モデルと分離多相流の組み合わせでは, レベルセット法が推奨されます. レベルセット法とフェーズフィールド法はどちらも, 下の図とアニメーションに示すように, COMSOL Multiphysics のすべての乱流モデルと組み合わせることができます.
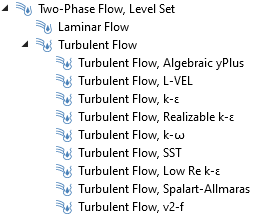
すべての乱流モデルは, COMSOL Multiphysics の二相流のフェーズフィールド法およびレベルセット法と組み合わせることができます.
レベルセット法と k-e 乱流モデルを組み合わせてモデル化した, リアクター内の水と空気の二相流.
分散多相流モデル
複雑なために相境界を解決できない場合は, 分散多相流モデルを使用する必要があります.
CFD モジュールは, 原則として4つの異なるモデルを提供します:
- 気泡流モデル
- 密度の高い相における軽い相の小さな体積分率用
- 混合モデル
- 分散相 (または複数の分散相) とほぼ同じ密度を持つ連続相における分散相の小さな体積分率用
- オイラー・オイラーモデル
- あらゆるタイプの多相流用
- 流動床など, 気体内の高密度粒子を含むあらゆるタイプの多相流を処理できます
- オイラー・ラグランジュモデル:
- 流体中に浮遊する比較的少数の (数十億ではなく数万) 泡, 液滴, または粒子の場合
- 各泡, 粒子, または液滴は, 流体内の各粒子の力のバランスを定義する方程式でモデル化されます
さまざまな分散流多相流モデル?
バブル流れ
バブル流れモデルは, 明らかに液体中の気泡に使用されます. 分散相からの運動量の寄与は無視されるため, モデルは分散相の密度が連続相よりも数桁小さい場合にのみ有効です.
混合
混合モデルは泡流モデルに似ていますが, 分散相の運動量の寄与を考慮します. これは, 液相中に分散した気泡または固体粒子をモデル化するためによく使用されます. 混合モデルは, 任意の数の分散相も処理できます. 混合モデルと気泡流モデルはどちらも, 分散相が連続相と平衡状態にあると想定しています. つまり, 分散相は連続相に対して加速できません. したがって, 混合モデルは気体中に分散した大きな固体粒子を処理できません.
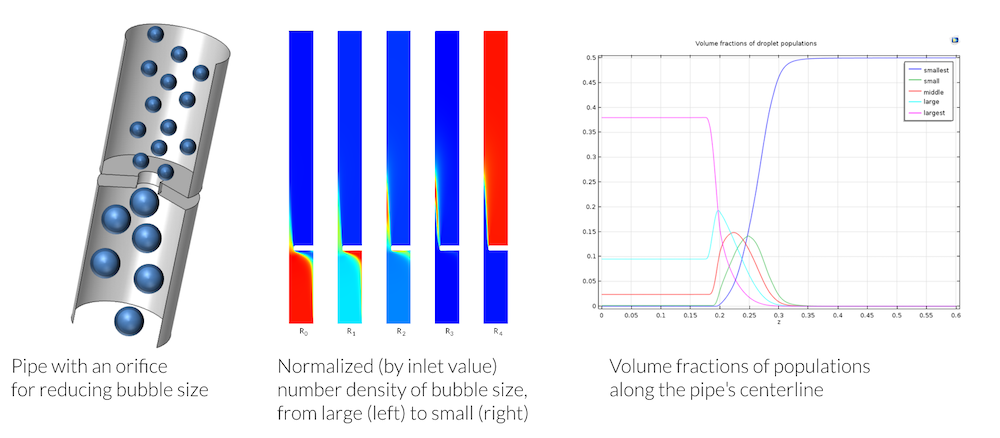
混合モデルは, 多相流混合物がオリフィスを通過する際に5つの異なるサイズの泡をモデル化するために使用されます. 流れのせん断により, 大きな泡が小さな泡に分解されます.
オイラー・オイラー
オイラー・オイラーモデルは, 最も正確な分散多相流モデルであり, 最も汎用性があります. あらゆる種類の分散多相流を処理できます. 分散相は加速することができ, 異なる相の体積分率に実際の制限はありません. ただし, 各相に対して1セットのナビエ・ストークス方程式を定義します.
実際には, オイラー・オイラーモデルは2相流にのみ適用可能で, その場合でも計算コスト (CPU 時間とメモリ) の点で高価なモデルです. また, 扱いが比較的難しく, 数値解の収束を得るには適切な初期条件が必要です.
オイラー・オイラー多相流モデルを使用してモデル化された流動床内の固体粒子の体積分率.
オイラー・ラグランジュ
連続流体に浮遊するごく少数 (数十万ではなく数万) の非常に小さな気泡, 液滴, または粒子がある場合, オイラー・ラグランジュモデルを使用して多相流システムをシミュレートできる場合があります. これらの方法には, 計算コストが比較的安価であるという利点があります. これらのモデルは, 数値的な観点からも 適切 です. したがって, 連続流体中に分散相の粒子が比較的少数である場合に好まれます.
なお, オイラー・ラグランジュ法では, 数十億の粒子を含むシステムを模倣できる相互作用項と体積分率を使用して, より多くの粒子を模倣する方法もあります. これらの方法は COMSOL Multiphysics で実装できますが, 定義済みの物理インターフェースでは使用できません.
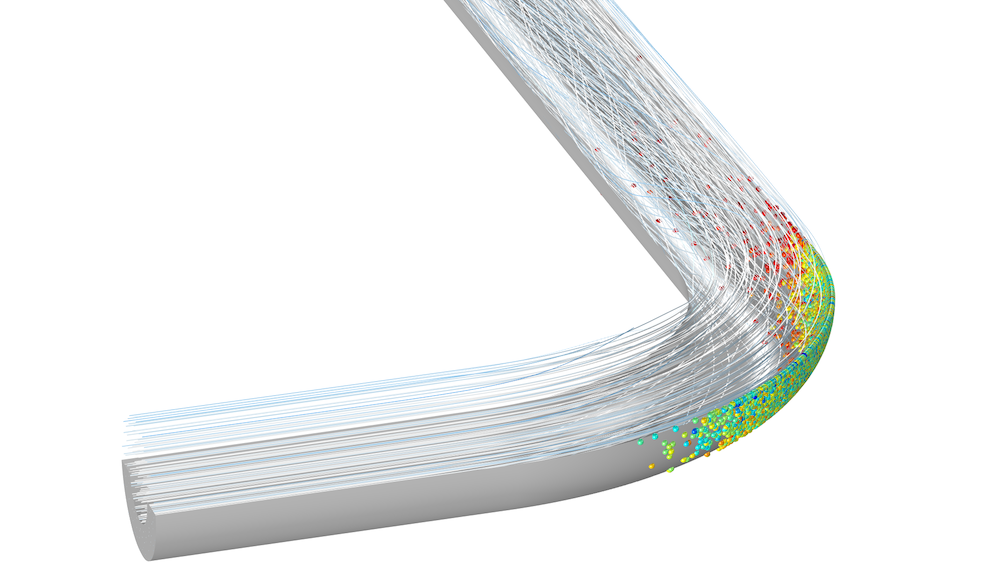
COMSOL Multiphysics のオイラー・ラグランジュ多相流モデルは, アドオン CFD モジュールと粒子追跡モジュール.
混合モデルは, あらゆる相の組み合わせを処理でき, 計算コストも低くなります. ほとんどの場合, このモデルから始めることをお勧めします. ただし, 流動床 (高密度で分散相の体積分率が高い大きな粒子) などのシステムを扱う場合は除きます. このシステムは, オイラー・オイラー モデルでのみモデル化できます.
分散多相流モデルと乱流
分散多相流モデルは本質的に近似的であり, 同じく近似的な乱流モデルと非常によく適合します. 分散相と連続相の間, および分散相内の気泡, 液滴, 粒子の間に相互作用を導入することが可能です. これらの相互作用は, 乱流モデルでモデル化された乱流渦に起因している可能性があります. 気泡流, 混合, およびオイラー・ラグランジュ多相流モデルは, COMSOL Multiphysics のすべての乱流モデルと組み合わせることができます. オイラー・オイラー多相流モデルは, 実現可能性制約のある標準 k-ε 乱流モデルに対してのみ事前定義されています.

混合モデルは, COMSOL Multiphysics の任意の乱流モデルと組み合わせることができます.
おわりに
多相流の数値モデル方程式を解くことは, スーパーコンピューターを利用できる場合でも, 非常に困難な作業になる可能性があります. コンピューターのパワー制限がなければ, 表面追跡法はあらゆる種類の混合物に使用されます. 実際には, これらのモデルはマイクロ流体工学と粘性液体の自由表面の研究に限定されています.
分散多相流法を使用すると, 数百万から数十億の気泡, 液滴, または粒子を含む系を研究できます. ただし, 最も単純な分散多相流モデルでも, 非常に複雑で困難なモデル方程式が生成される可能性があります. これらのモデルを, 特定の混合物の記述に適したバリエーションに発展させることで, エンジニアや科学者は比較的高い精度と妥当な計算コストで多相流を研究できるようになりました.
ブログでは多相流シミュレーションについて引き続き取り上げますので, どうぞお楽しみに!






コメント (0)