
モデリングとシミュレーションに関する室内音響の課題の1つは, 周波数範囲全体にわたって部屋を正確にモデリングすることです. このブログでは, COMSOL Multiphysics® ソフトウェアで室内音響をモデリングするためのハイブリッドアプローチについて説明します. このアプローチでは, 複数の方法の結果を1つのモデルに統合することで, 精度を向上させ, 実現可能性を維持します. その方法を学びましょう.
室内音響のレビュー
前回のブログ COMSOL Multiphysicsによる室内音響のモデリングでは, 音響モジュールで利用可能な複数の手法について説明し, 密閉空間の音響をモデリングする方法について説明しました:
- 圧力音響インターフェースによるモード動作
- 音線音響インターフェースによる高周波動作
- 音響拡散方程式インターフェースによる高周波動作
今日は, 最初の2つの方法を組み合わせて部屋の広帯域インパルス応答を取得する方法について説明します.
室内インパルス応答
空気で満たされた風船が部屋の中で破裂し, 部屋の別の場所にあるマイクが音圧を時間の関数として記録するところを想像してください. マイクは, 最初の波面からの直接音と, 部屋の壁, 床, 天井, その他の物体を伝わって跳ね返る波からのすべての反射信号の重ね合わせを受信します. 音は通常, カーペット, 家具, 天井タイルなどのさまざまな素材によって吸収されるため, 音は最終的に完全に消えて再び静かになります. マイクによって記録された音圧対時間信号は, その測定場所における室内インパルス応答と呼ばれます. これは, 部屋の音響特性を記述する非常に重要なもので, 部屋の音について多くのことを伝えます.
左: 音線音響モデルの結果は, 音源からマイクの位置までの音線の一部の経路を示しています. 右: 室内のインパルス応答の例.
部屋のモデリング
部屋の音響をモデル化する場合, モデリングアプローチの精度と実現可能性を判断するために, 音響スケールと幾何学的スケールの両方に注意を払う必要があります. 音響モジュールでは, 圧力音響 (周波数領域) インターフェースを使用して, 有限要素法で部屋の低周波のモーダル動作をモデル化できます. ただし, このアプローチはメッシュ要件のため, 高周波では計算コストが高くなります. 部屋の高周波の反響動作は, 音線音響インターフェースを使用して音線追跡法でモデル化できます. この方法は一般的に計算効率が高いですが, 音線追跡は波動ベースの方法ではないため, モーダル動作を捕獲しません. 部屋のインパルス応答を正確にモデル化するには, 両方のモデルをそれぞれの周波数範囲で実行し, 組み合わせて周波数範囲全体にわたる応答を取得します.
4.7 x 4.1 x 3.1 m の長方形の部屋を考えてみましょう. この例のすべての壁は, 周波数に依存する吸収係数でモデル化されています. このモデルの目的は, 座標 (3,3,2) m にあるマイクのインパルス応答を決定することです. 単極インパルス音源の場合, 軽い吸収壁を考慮すると, 部屋のどの点でも圧力の3次元解析解が存在することがわかります. 参考文献1および参考文献2では, 任意の点における圧力 P(r) は, グリーン関数 G(r,r_0) で表すことができます. これは, レシーバー (r) とソース (r0) の位置で評価された減衰のない室内モード形状と, 周波数依存の減衰項 \tau_{mnp} から構成されます. 式は次のとおりです:
ここで, \rho_0 は密度, \omega は周波数, Q は単極子領域の音源体積速度です. グリーン関数は, 3つの直交直交方向のモードの3重和を表し, インデックス m n p は異なるモードを表します. \psi は, モード k_{mnp} のモード形状 (コサイン関数の積) を表し, \Lambda_{mnp} は, 体積 V の部屋のモード整数係数です. 波数は k です. 解析解の完全な説明については, 参考文献1および参考文献2を参照してください. このモデリングシナリオでは, 解析解を定義する変数が コンポーネント1 > 定義 > 変数1 – 解析解 に追加されています.
この 以前のブログで説明したように, モードと残響のある部屋の動作の間には明確な遷移周波数はありませんが, Schroeder が提案した基準に基づいて推定できます (参考文献3, 4). この場合, Schroeder 周波数は 370 Hz に近く, グローバル定義 > 音線パラメーター で計算されます. 上記の解析解は, 数値モデルと比較するための参照解として機能します.
圧力音響
理想的には, 全周波数範囲にわたって波動ベースの方法を使用して部屋をモデル化したいのですが, メッシュ要件のため, 高周波数では実現できない可能性があります. 個々のモードの寄与が Schroeder 周波数以下の部屋の応答を支配することがわかっているので, Schroeder 周波数よりも少し高い最大周波数 (この場合は最大 500 Hz) を使用して圧力音響を解くことを選択します. 圧力音響モデルの設定は以下の通りです:
- 圧力音響 (周波数領域) インターフェースを備えた3Dコンポーネント
- 一定電力の単極点音源
- 周波数依存インピーダンス条件 (吸収係数) が規定された壁
- 500 Hz の空気中の波長を分解する体積メッシュ
- 周波数領域スタディ
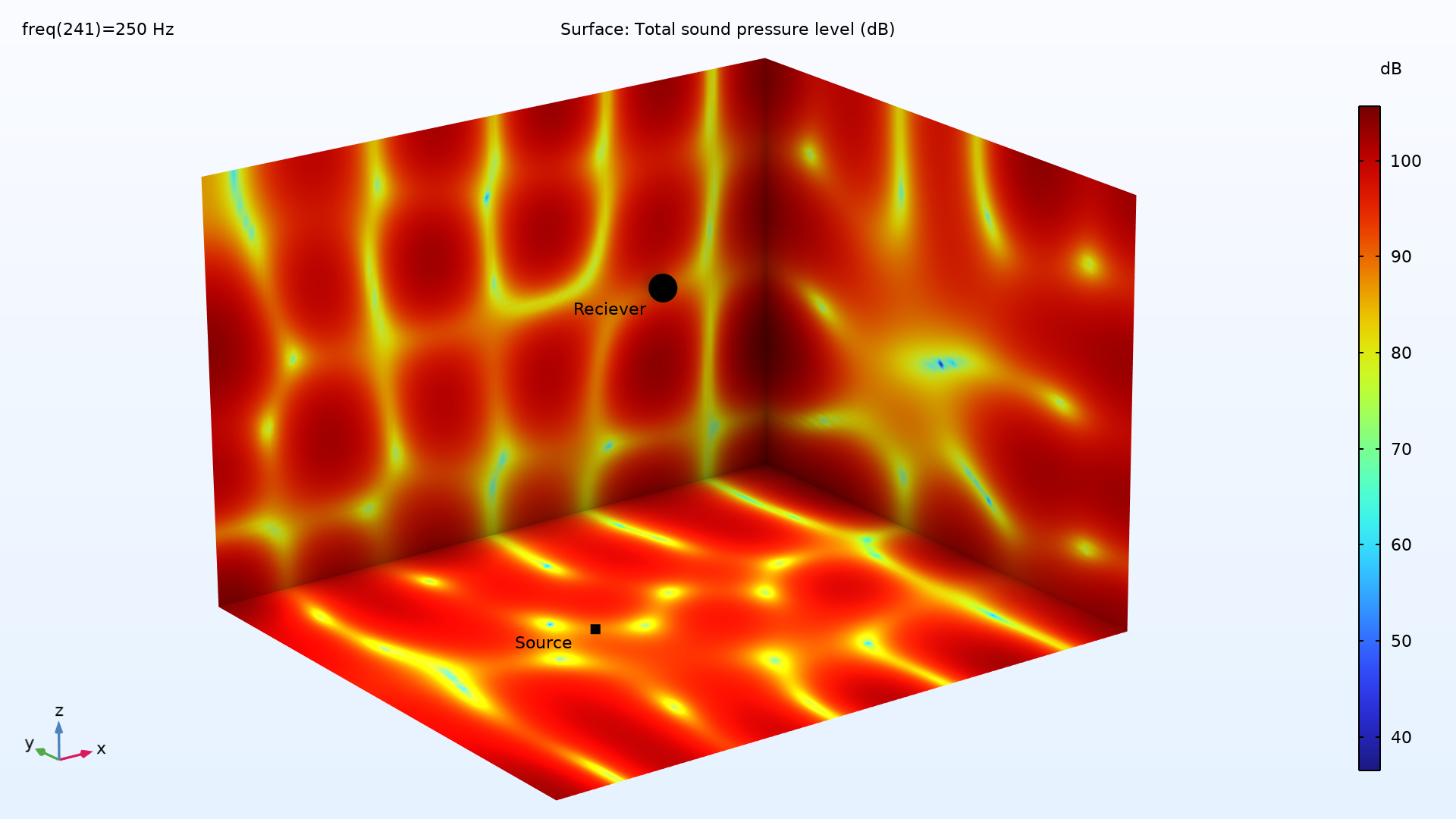
250 Hz における長方形の部屋の3つの壁の音圧レベル (dB ref. 20 µPa).
上のグラフは, 部屋の壁の一部における音圧レベル分布の例を示しています. この方法を使用すると, 部屋の低周波 (500 Hz以下) の挙動がモデル化されました. 部屋の高周波の挙動をモデル化するには, 音線音響に切り替えます.
音線音響
音線音響モデルは次のように設定されています:
- 音線音響インターフェースを備えた3Dコンポーネント
- 周波数依存の吸収係数が規定された壁
- 規定されたパワーでソースポイントから8000本の音線を出射するグリッドから出射条件
- パワーレベルがしきい値を下回った場合に音線の追跡を停止する (これにより自由度が減少する) 音線追跡中止基準
- 4000 kHz までの 1/3 オクターブバンド周波数にわたるパラメトリックスイープによる音線追跡スタディ
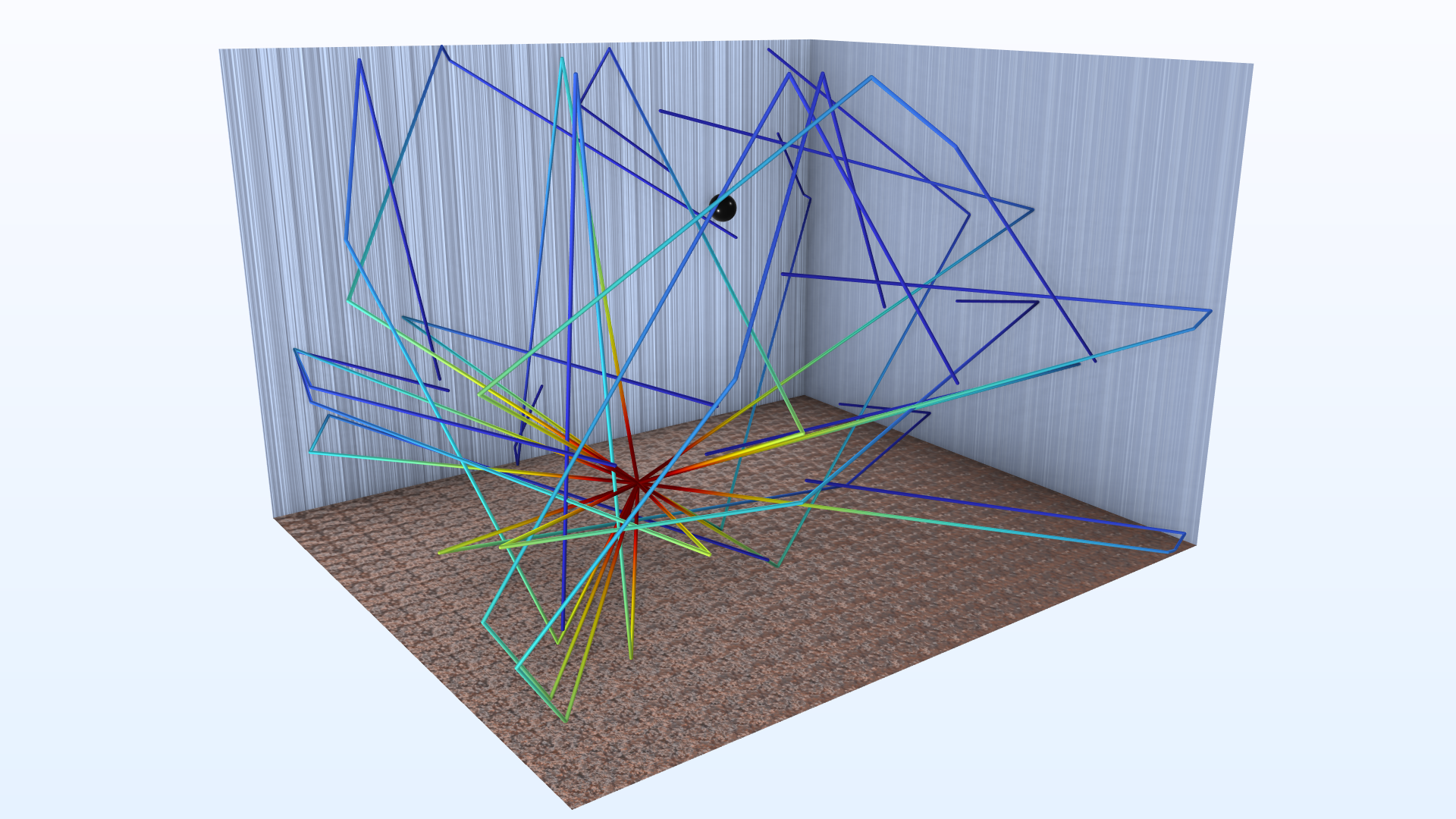
下の画像は, 点光源から放出された光線のスナップショットです. 視覚化のため, 光線の一部のみが下に示されていることに注意してください (光源の位置より小さい y 座標を持つ光線は非表示になっています).

3 ms での音線の軌跡は, 単極点音源からの音線の出射を示しています. カラースケールは Pa での音線圧力を表します.
音線追跡スタディは, 周波数の細かいステップでは実行されません. では, インパルス応答はどのように計算されるのでしょうか. COMSOL Multiphysics には, このための専用のレシーバーデータセットとインパルス応答1Dプロットグループがあります. このプロットグループは, 音線パワー, 周波数, 反射数, 流体特性などの 1/3 オクターブバンド入力を受け取り, 周波数に対するインパルス応答を再構築します. 目標は, 入力オクターブバンドで平均化したときに, 実際の信号と同じエネルギー内容を持つ新しい信号を取得することです. これは, 選択した IR フィルターカーネル (デフォルトは, カイザーウィンドウを使用したブリックウォール) でインパルス信号を畳み込み, すべての周波数バンドのすべての音線からの寄与を合計することによって行われます. 再構成の詳細については, 音響モジュールユーザーガイドを参照してください.
下のグラフは, マイクの位置での音圧レベルを示しています. 単極点音源は時間内のインパルスを表すため, 音源が周波数上の広帯域励起である周波数領域で室内インパルス応答を解釈することもできます (時間内のディラックデルタ関数のフーリエ変換は, 周波数の定数関数です).
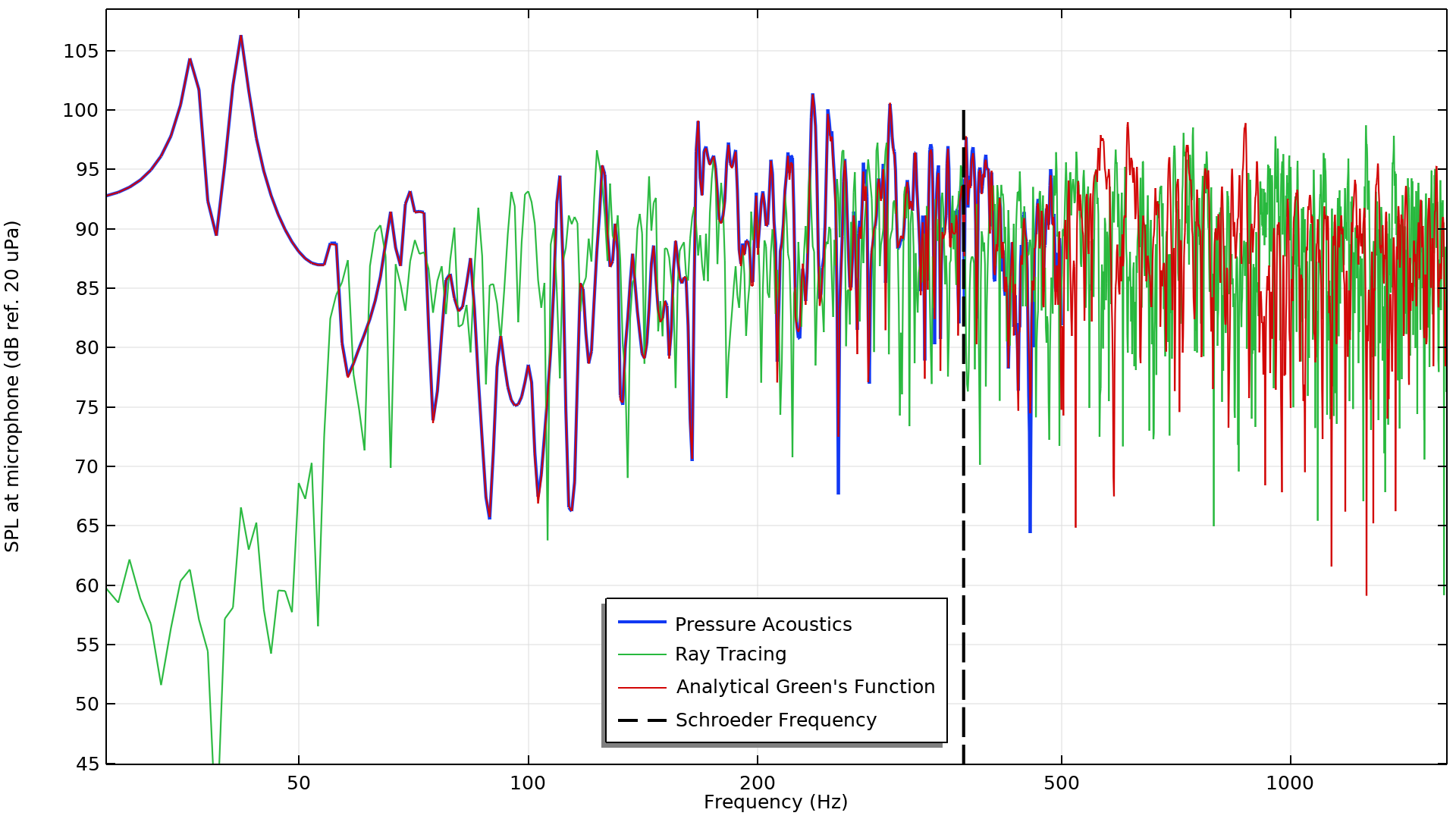
圧力音響スタディ, 音線追跡スタディ, および解析式によって計算されたマイクロフォンでの音圧レベル. 黒の破線は Schroeder 周波数を表します.
このプロットに基づいて, いくつかの重要な結論を導き出すことができます. まず, 解析結果は, そのスタディの最大周波数である 500 Hz まで, 圧力音響スタディの結果とよく一致しています. この結果は, モデルが正しく設定されていることを示す優れたベンチマークとして役立ちます.
音線追跡の結果を他の結果と比較すると, 低周波の音圧レベルが一致していないことは明らかです. 音線追跡は本質的に波ベースの方法ではなく, 低周波で支配的なモード動作を捕獲しないため, これらの結果は予想どおりです. このモデルでは, 音線追跡の結果は低周波, 特に 50 Hz 未満では正確ではないと結論付けることができます.
圧力音響プロットの最初の2つの共鳴ピークは, 衝撃音源によって励起され, 音響エネルギーが壁によって強く吸収されていない2つの異なるモードに対応しています. モデルでは音吸収を考慮しているため, ここでのモードは音響ハード壁を持つ部屋のモードとほぼ等しくなります. 参考文献5は, 剛性境界条件を考慮して, 同じサイズの部屋 (4.7 x 4.1 x 3.1 m) の最初の20モードを導出して計算しています (参考文献5の表 3.1 を参照). 最初の2つのモードは, 36.17 Hz の (1,0,0) モードと 41.46 Hz の (0,1,0) モードです. これらは, それぞれ x 方向と y 方向の最初のモードに対応し, 上のプロットの最初の2つのピークとよく一致しています.
117 Hz 未満には20のモードがあり, 周波数が増加するにつれて, 部屋の反響動作に寄与するモードの数が増えます. 低周波数では, モードの間隔は広く, モードの帯域幅は重なりません. 高周波数では, モードは重なり, ノイズの多い周波数応答になります. 音線追跡は波動ベースの方法ではないため, 音線追跡の結果は, Schroeder 周波数以上でも解析結果と完全に一致するとは予想されません. ただし, 音線追跡と解析結果はどちらも, Schroeder 周波数以上では同様の特性と音圧レベルの範囲を示しています. つまり, Schroeder 周波数以上の音線追跡の結果を使用して, 入力オクターブバンドで平均化したときに実際の信号と同じエネルギーコンテンツを維持するという基準に基づいて, インパルス応答を正確に推定できます.
組合わせ法
圧力音響モデルと音線音響モデルの結果を組み合わせて, 広帯域のインパルス応答信号を作成できます. 参考文献6で説明されている方法と同様に, これは, ローパスフィルターされた圧力音響応答を取得し, それをハイパスフィルターされた音線音響応答に追加することで実行できます. この方法では, フーリエ変換の線形特性を活用します.
使用するフィルターの種類と信号をフィルターする場所の指定は, 工学標準としては設定されていません. 実装されたデジタル信号処理手法は, 業界固有の慣行または工学的判断に基づいて選択できます. このモデルは, Schroeder 周波数で信号をフィルターする単純な理想的なステップフィルターを使用して, 組み合わせの概念を示しています.
信号の組み合わせは次のように設定されます:
- グローバル ODE および DAE インターフェースを備えた0Dコンポーネント
- 音線音響モデルの結果はファイルにエクスポートされ, 補間曲線としてコンポーネント3にインポートされます
- 圧力音響モデルの結果は, スタディ設定の従属変数の値を使用してスタディ3に渡されます
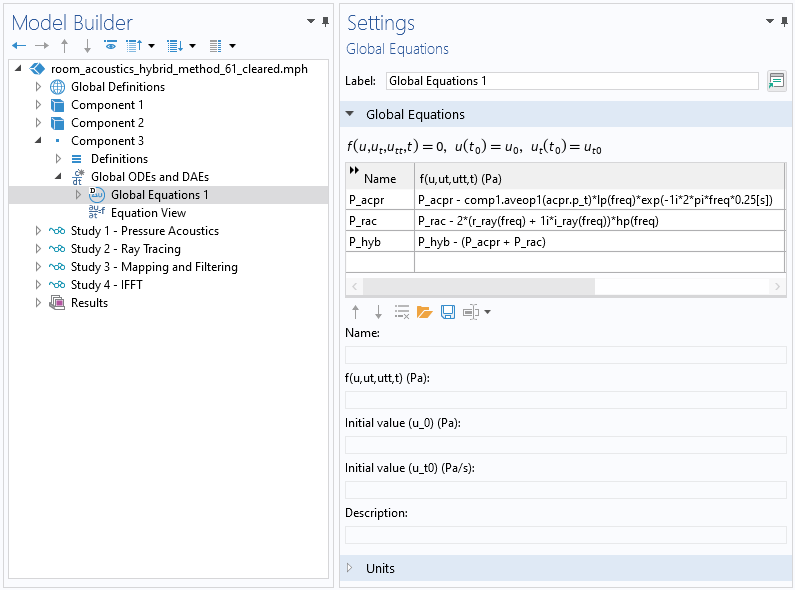
次のグローバル方程式がコンポーネント3に追加されます:
ここで, P_acpr はレシーバーでの体積平均圧力です. 式は, 圧力がローパスフィルターされ, 後で比較できるようにインパルス応答プロットタイプの規則に一致するように時間的にシフト (0.25秒ずつ) されることを示しています. P_rac は, インパルス応答高速フーリエ変換 (FFT) の補間関数からの圧力です. P_rac 式は, 補間関数 r_ray と i_ray (音線追跡スタディ スタディ2からの圧力の実数部と虚数部) を使用します. 圧力式は, 音線圧力がハイパスフィルターされ, 2倍になることも示しています. 係数が2なのは, 補間値がフルスペクトル用であるのに対し, スタディ3では正の周波数のみが計算されるためです. 最後に, P_hyb は, ローパスフィルターされた圧力音響応答とハイパスフィルターされた音線追跡応答の合計です (参考文献6で使用されているものと同様のアプローチを使用).
以下のプロットは, コンポーネント3のみを使用して周波数領域スタディを実行した後の元の信号と結合信号の比較を示しています. ここでは, 圧力音響と音線追跡の両方の結果を組み合わせることで, ハイブリッド応答に正しい周波数コンテンツが含まれていることがわかります.
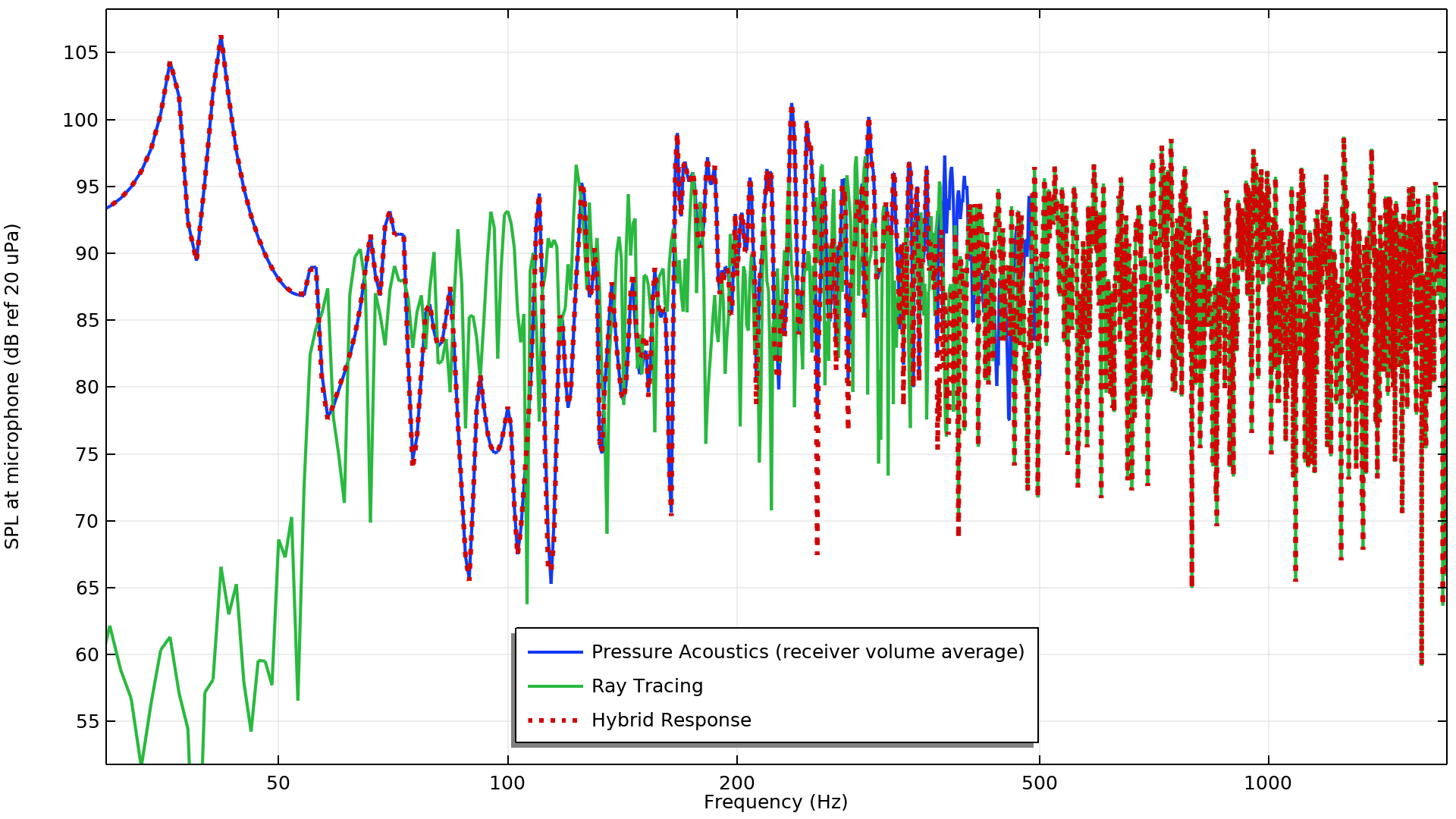
圧力音響, 音線追跡, ハイブリッド法によって計算されたマイクでの音圧レベル.
理想的なフィルターは, ハイパスフィルタ hp(freq) では0から1にステップし, ローパスフィルタ lp(freq) では1から0にステップするステップ関数を使用して実装されます. 両方の関数に 50 Hz の滑らかな遷移ゾーンが含まれており, ステップ遷移の位置は Schroeder 周波数に設定されています. これらの関数は両方とも, コンポーネント3 > 定義 の下に追加されます. Schroeder 周波数付近のハイブリッド応答を詳しく見ると, 次の図のようになります. このプロットから, 理想的なフィルターの特性を分析できます. 特に, 理想的なフィルタは両方とも Schroeder 周波数でゲイン係数が -3 dB であるため, ここでの応答は両方の平均です. 他の場所では, ハイブリッド応答は周波数に応じて両方の応答の加重組み合わせです. フィルターの合計はすべての周波数で 0 dB です.
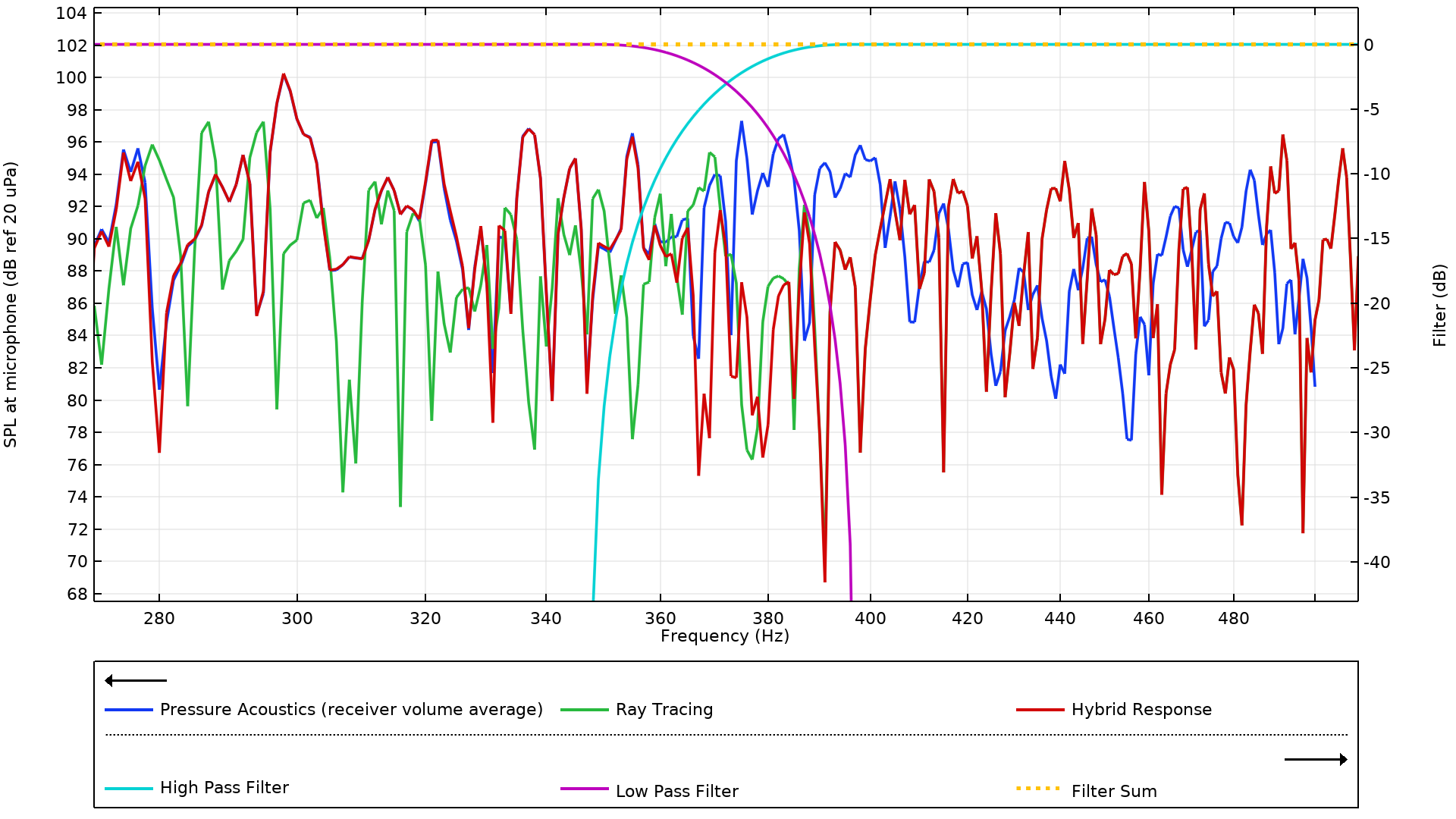
Schroeder 周波数付近のフィルター平均ハイブリッド圧力.
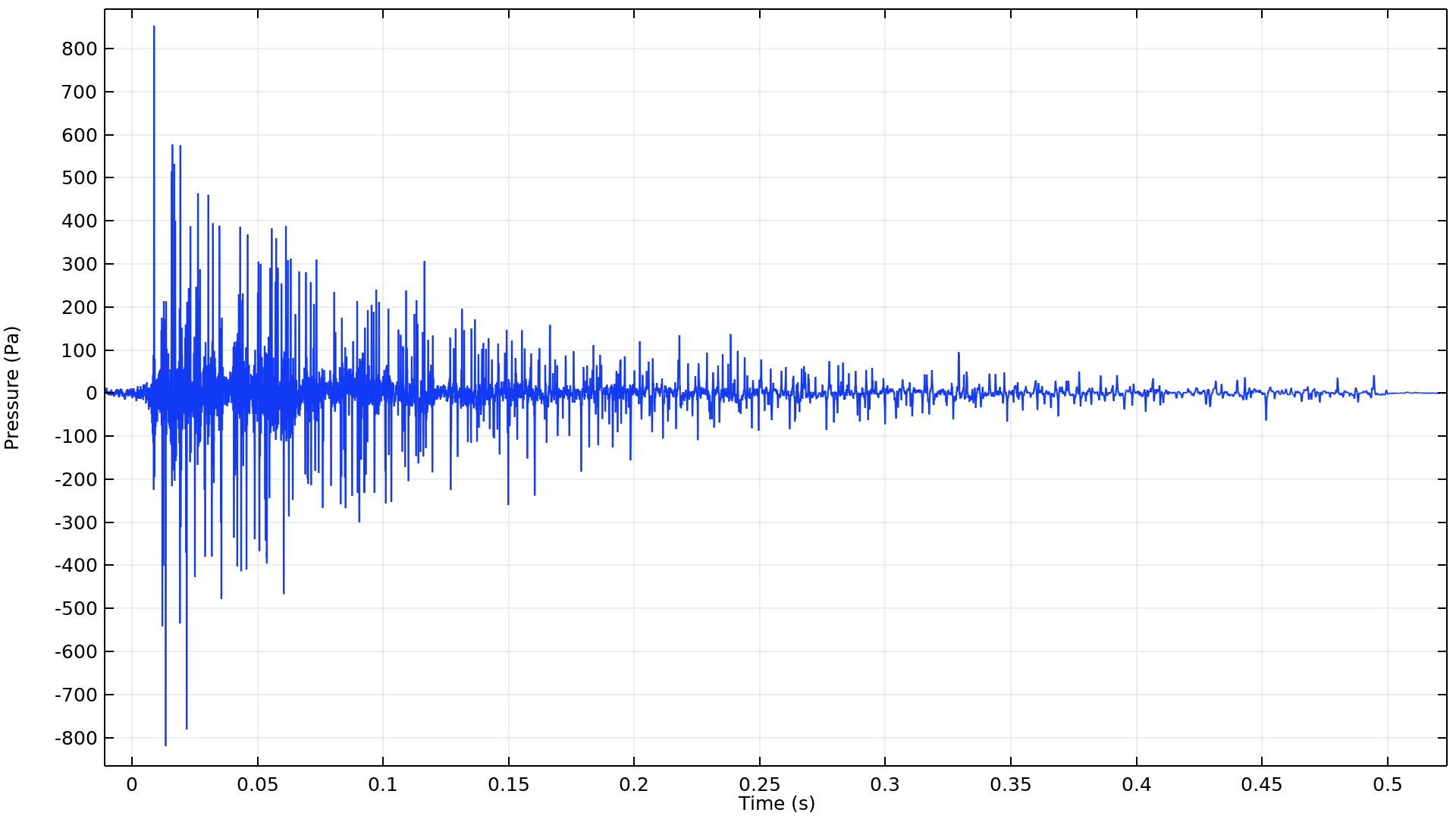
応答を時間領域に戻すために, 周波数から時間への FFT ステップを含む4番目で最後の調査が実行されます. このステップでは, Tukey ウィンドウ関数を使用して逆 FFT (IFFT) を帯域制限します. ハイブリッド信号と元の音線追跡信号の比較を以下に示します. 時間領域でいくつかの違いが見られますが, 周波数スペクトルを直接確認すると違いを見つけやすくなります. ここで計算されたハイブリッド圧力対時間信号は, 周波数範囲全体にわたって純粋な音線追跡信号よりも正確であることは明らかです. この精度は, ハイブリッド信号を使用して明瞭度, 残響時間, 音声伝達指数などの他の室内メトリックを計算したり, 部屋の可聴化用の外部分析ツールで使用するためにエクスポートしたりできることを意味します.
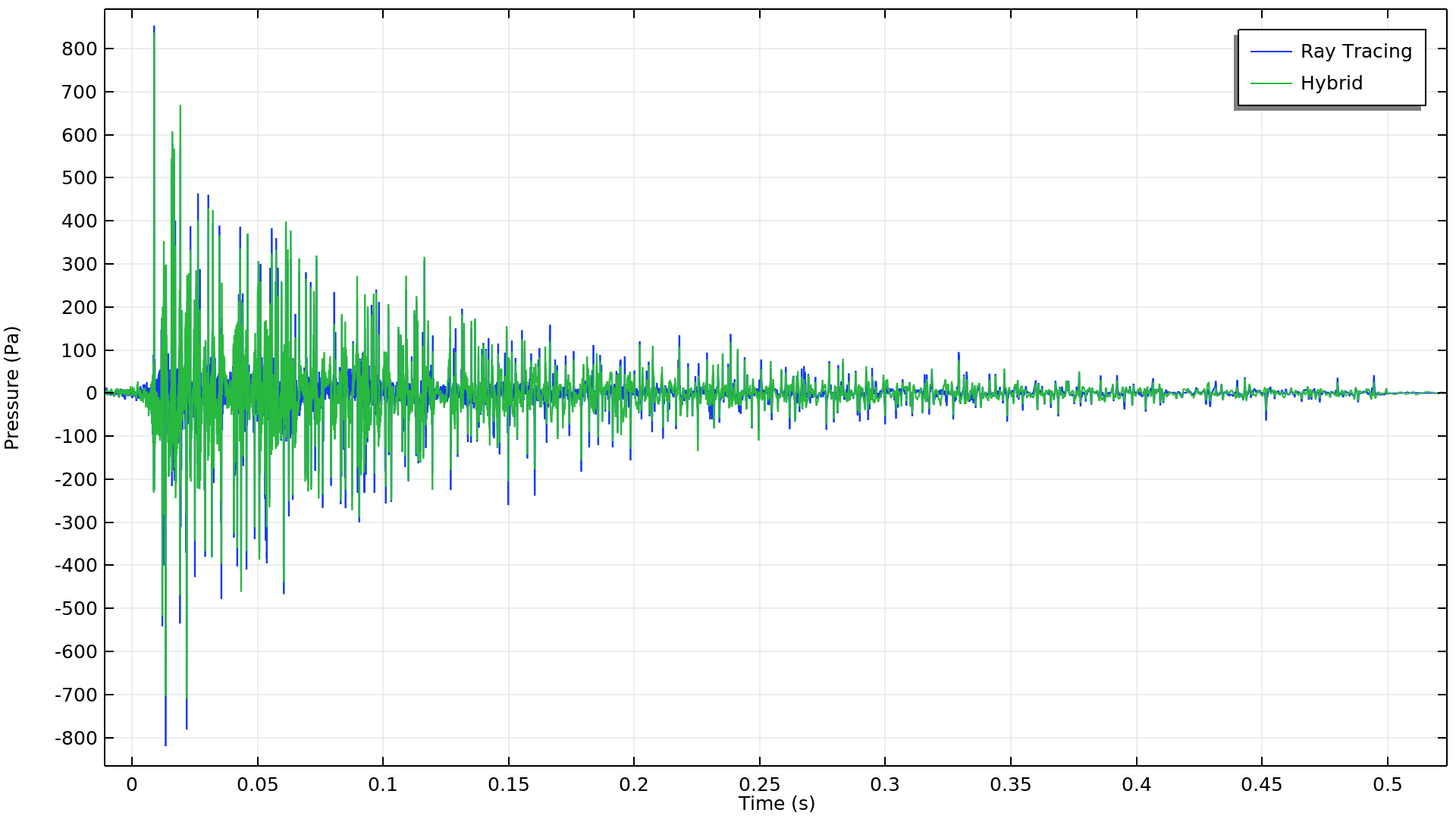
音線追跡法とハイブリッド法の圧力対時間インパルス応答の比較.
自分で試す
ここでは, 音線追跡と有限要素法を組み合わせて広帯域インパルス応答を得るための1つのアプローチを示しました. すべてのモデリングは COMSOL Multiphysics で完了し, ソリューションは1つのモデルに統合されています. このアプローチは, 高周波で完全波動法を使用することが必ずしも実現可能ではない大きな部屋で特に役立ちます. 下のボタンをクリックして, アプリケーションギャラリからモデルファイルをダウンロードして, 自分で試してみてください:
他の参考文献
より多くの室内音響モデルをご覧になりたい場合は, アプリケーションギャラリで関連モデルをご覧ください:
- 室内楽ホール: ベルリンコンツェルトハウスの小ホールの音響を音線追跡でシミュレートする.
- 車室内音響 – 周波数領域解析: 車室内の音響は圧力音響を使用してモデル化します. 反復ソルバーを使用して, 4 kHz までのモデルを解きます.
参考文献
- Morse, Philip McCord, and K. Uno Ingard. Theoretical Acoustics. Princeton University Press, 1986.
- Okoyenta, Augustus R., et al. “A Short Survey on Green’s Function for Acoustic Problems.” Journal of Theoretical and Computational Acoustics 28.02 (2020): 1950025.
- M. R. Schroeder, New Method of Measuring Reverberation Time, J. Acoust. Soc. Am., 37 (1965).
- M. R. Schroeder, Integrated-Impulse method measuring sound decay without using impulses, J. Acoust. Soc. Am., 66 (1979).
- Kuttruff, Heinrich. Room Acoustics. CRC Press, 2016.
- Aretz, Marc, et al. “Combined broadband impulse responses using FEM and hybrid ray-based methods.” EAA Symposium on Auralization, 2009.



コメント (0)