地球上のすべての生命は, リボ核酸 (RNA) またはデオキシリボ核酸 (DNA) という2つの密接に関連した高分子によってコード化されています. ある意味では, 地球上には1種類の生命しか存在しないと言えます.
ウイルスは生命と呼べる限界の生き物です. ウイルスは RNA や DNA を持っていますが, 独自の成分を生成することはできず, 他の生細胞の外で繁殖することはできません.
ウイルスが繁殖するには, 生細胞と接触し, 宿主細胞の受容体に適合し, 宿主細胞の膜を開く必要があります. その後, ウイルスは RNA または DNA を注入し, 宿主細胞の代謝を乗っ取って新しいウイルス粒子を生成します.
ウイルス粒子は生細胞外で生存する能力が非常に限られているため, 拡散の主なメカニズムは生物間の接触です. 新型コロナウイルス感染症 COVID-19 の原因ウイルスである SARS-CoV-2 の場合, 直接的または間接的にヒトからヒトに伝染する必要があります. COVID-19 は世界保健機関 (WHO) によってパンデミックに分類されています.
しかし, パンデミックの進行状況を把握することは可能でしょうか? 感染者は何人になるでしょうか? 死亡者は何人になるでしょうか? そのようなモデルがどのようなものになるか見てみましょう.
COVID-19 の数学的モデル
ヒトからヒトへの感染を合理的に予測できる最も単純なモデルの1つは, いわゆる SEIR モデルです. このモデルは, 1920年代頃に最初の形で公開されました (文献 1, “The SIR model and the Foundations of Public Health“). このモデルは, 流行中の人口を4つの異なるコンパートメントに分割し, 各コンパートメントの個人の数に異なる変数を設定します:
S = 感受性
E = 感染
I = 感染性
R = 回復し免疫がある
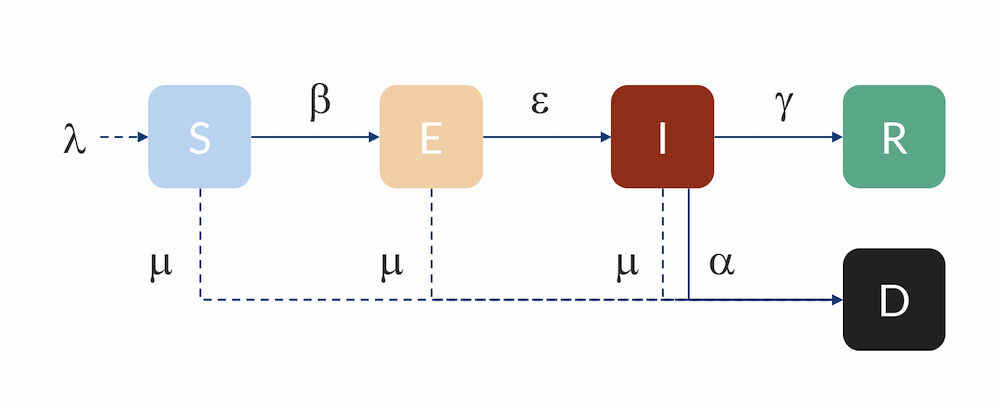
コンパートメントモデル: 個体は, S コンパートメントから E コンパートメントに速度 β で, E コンパートメントから I コンパートメントに速度 ε で, I コンパートメントから R コンパートメントに速度 γ で流れます. 個体は, I コンパートメントから D (死亡) に速度 α で流れることもあります. R コンパートメントの個体は, ここでは免疫があると想定されており, モデルの期間中は S コンパートメントに戻りません. 新生児の流入は λ で表され, 自然死亡率は μ で表されます.
S, E, I, R 変数の単位は個体数です. 感受性区画内の個体が感染するには, 感染者と何らかの接触をする必要があります. このような感染の確率は, 感染者の割合と集団内の感受性者の数の積に関係しています. 整理すると, 感染率は次のようになります.
(1)
ここで, β は感染率です.
β (単位: 1/日) は, 感染者が平均して感染させる人数 R0 と, 人が感染力を持つ平均日数 (隔離または自己隔離する前) nid に関連しています:
(2)
R0 は 基本再生産数 (無次元) と呼ばれ, 感染者が感染しやすい人と接触するたびに (集団に免疫がまったくない場合) その人が回復するまでの病気の広がりを表します. あらゆる緩和策や封じ込め策は, 感染率 β を下げるか, 感染者が隔離されるまでの時間を短縮することによって, 再生産数を減らすことを目指します.
より短い (季節性のない) 流行シミュレーションでは, 自然死と出生が均衡している一定の人口を想定できます. すると, 感染しやすい人の数は, 新しい感染例の増加とともに減少します. ここで, N は人口の大きさを表します:
(3)
同様に, 上記の式の右側の項は, 感染者数 E の式のソース項です. ただし, この式には, 感染者が E コンパートメントを離れて感染性になるという負の項もあります.
(4)
ここで, ε は, 曝露後に感染性に進行する速度を1日あたりの単位 (1/日) で表します. 速度は潜伏期間の長さに反比例します.
感染者数 I は, 1日あたりの εE とともに増加しますが, 個人が隔離, 回復, または死亡する速度とともに減少します. 速度係数 γ は, 人々が隔離または回復する速度を表します. この率は, 感染している日数に反比例します.
(5)
感染者が病気で死亡する率を表す用語 αI もあり, 感染変数 I の式は次のようになります:
(6)
感染しにくい個体数を表す R の変数の式は次のとおりです:
(7)
死亡する個体数 D の式は次のとおりです:
(8)
曲線の平坦化
まず, 曝露の変数を考慮しない, より単純なモデルを見てみましょう. つまり, 感受性の高い個体が感染した個体と出会い, 感染します. このモデルでは, これは ε の非常に大きな値に相当します. 次に, 同じ方程式を解いた Michael Höhle のブログと比較することができます (文献 2, “Flatten the COVID-19 curve“). 入力データは次のとおりです:
N = 100 万人
R0 = 2.25, 基本再生産数
nid = 5 日
最後に, 初期条件が必要です:
S0 = N – I0 感受性者
I0 = 10 人の感染者
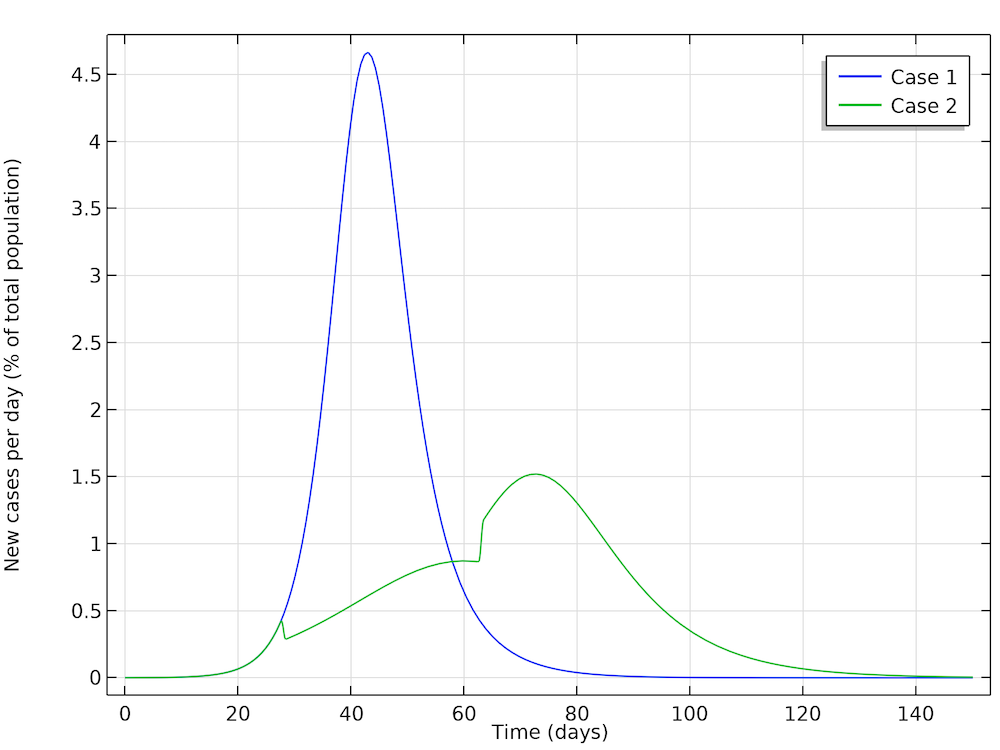
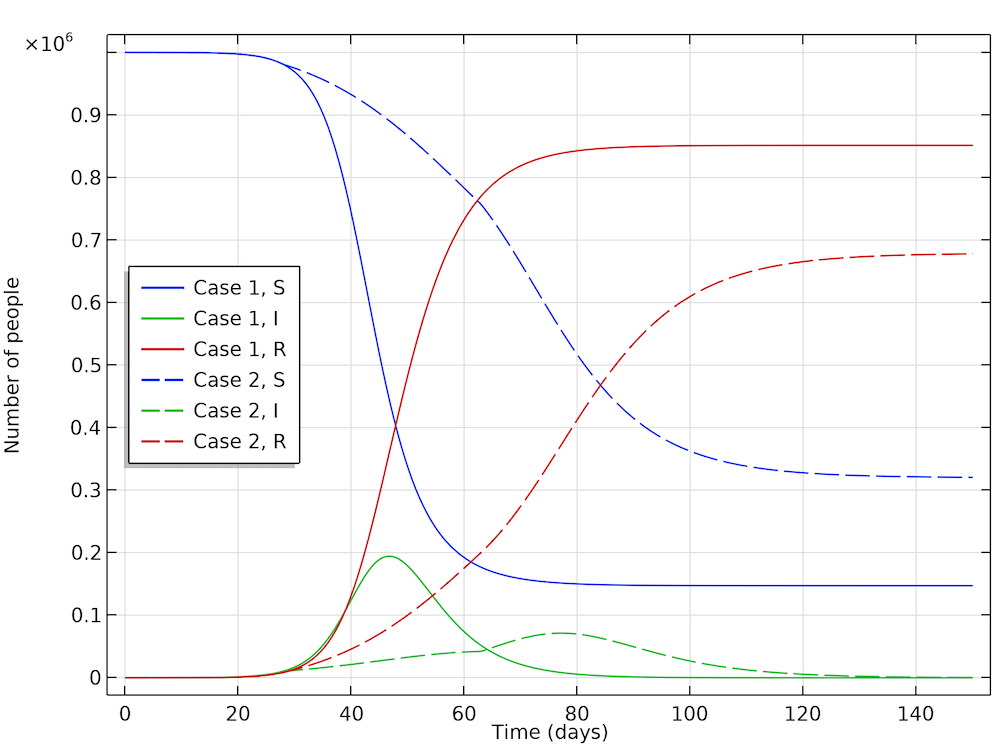
最初のケースでは, Höhle は, 人口の社会的距離の制限なしに流行が進行することを許可したシミュレーションを実行します. 2番目のケースでは, Höhle は, 人口100万人の都市の当局が, たとえば大規模なグループの集まり (スポーツイベント, コンサートなど) を許可しないなど, 再生産数を減らすための措置を講じると想定しています. 最初のステップは, 社会的交流の制限を導入することで, 流行の28日後に基本再生産数を 1.35 まで下げることです. この下げ幅は5週間維持され, その後対策が緩和され, 再生産係数は再び 1.8 まで上昇します. 下の図は, ケース1 (対策なし) とケース2 (R0 の減少) の2つのケースを示しています. Höhle の結果と非常によく一致していることがわかります.
Höhle が定義した2つの事例. ここで得られた結果は, Höhle の結果と非常によく一致しています. 再生産数を減らすために講じられた措置は, 28日後に緑の曲線で新規症例が急激に減少し, その後突然増加するという形で表されます.
ケース2 (Höhle 氏) の興味深い結論は, 新規症例の再生産を減らすために講じられた措置は, 特定の時点での新規症例数を減らすだけでなく, 流行が終息する前に感染する人の数も減らすということです. 結果は下の図に示されています. ケース1では流行が終息する前に感染する人口の割合は 85% ですが, ケース2では 68% にすぎません. つまり, 措置は医療システムへの負荷を一時的に軽減するだけでなく, 流行全体を通して患者総数も減らします.
対策を講じなかった場合に感染する集団の割合は 85% で, 回復曲線 (赤, 実線) に示されています. 一方, 対策を講じた場合, 68% が感染します (赤, 破線).
流行の進行中の人口分布の考慮
湖北省, スウェーデン, 米国については, もう少し高度なモデル, いわゆる Erlang–SEIR モデルを使用できます (文献 3, “Discrete Stochastic Analogs of Erlang Epidemic Models“). E および I コンパートメントをサブコンパートメントに分割すると, 各コンパートメント内の個人の滞在時間は, 指定された平均滞在時間を持つアーラン分布に従います. 平均滞在時間は, サブコンパートメントの数 kE および kI に比例し, サブコンパートメント間の移動率 ε および γ に反比例します. このモデルは, たとえば, 感染した症例が国のさまざまな地域でさまざまな時間に入国するため, さまざまなコンパートメント間の流れに分布があるという事実を説明できます. サブコンパートメントの数を増やすと, 分布は平均の周りに集中し, 実質的に E から I へ, および I から R および
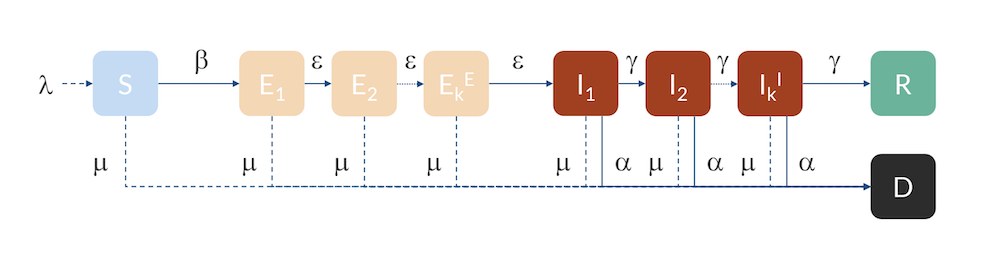
E と I のサブコンパートメントを備えた Erlang–SEIR モデル.
中国がロックダウン
このモデルを使用して, 流行が始まった湖北省のデータに対して パラメーター推定を実行 できます. 感染者数は信頼できるデータではないことはわかっています. なぜなら, 大多数の人は検査を受けておらず, COVID-19 と診断されていないからです (文献 4, “Estimates of the severity of coronavirus disease 2019: a model-based analysis“). 最も信頼できるデータはおそらく死亡者数でしょう.
死亡率を 0.66% (文献 4), 隔離前の感染期間の平均を3日, 症状の発現から死亡までの期間を平均18日と仮定すると, 流行の開始, 感染率, 曝露状態の平均時間を湖北省から報告されたデータにエルラン分布で当てはめることができます.
1月22日に当局はロックダウンを実施し, その月末の測定では基本再生産数が明らかに減少していることが示されています (文献 5, “Early dynamics of transmission and control of COVID-19: a mathematical modelling study“).
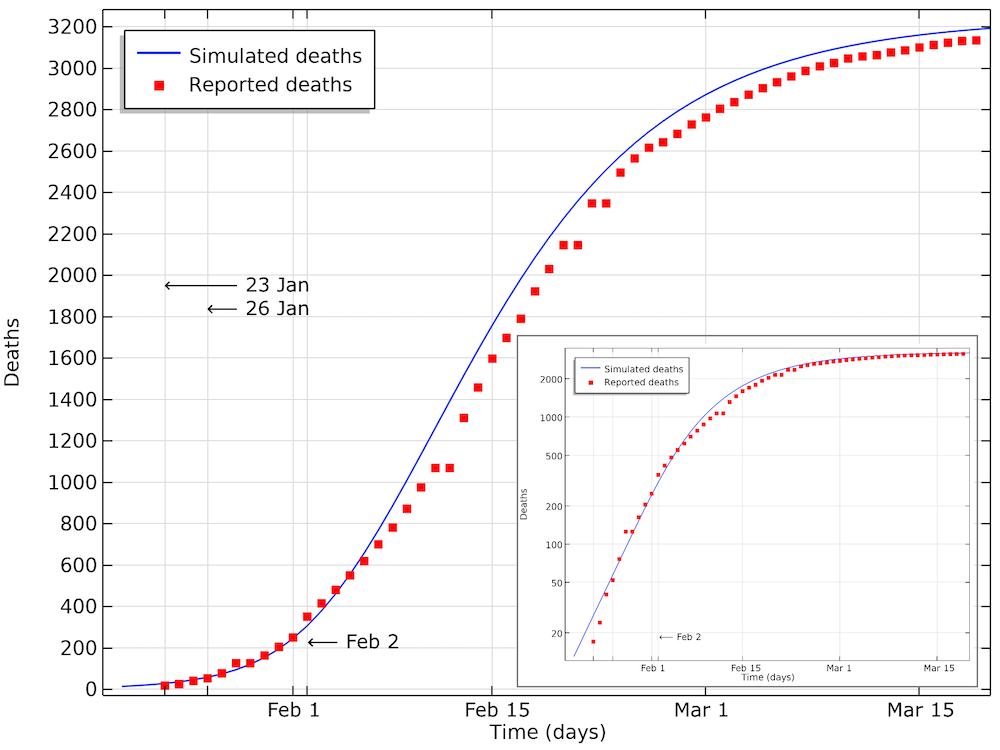
このような削減を実施し, その削減の影響を1月23日の発症に当てはめると, 以下の結果が得られます.
湖北省で報告されたデータと比較した死亡者数のモデルデータ. モデルはデータとよく一致しており, 半日か1日のわずかなずれがあることがわかります. このずれは, 死亡者数の増加に伴う報告の遅れによって説明できます. 小さい方のグラフは, 同じデータを y 軸の対数スケールで示しています.
上のグラフでは, 累積死亡者数が2月2日までに約400人になるまで, 対数プロットで直線的に指数関数的に増加していることがわかります. 2月3日以降, 死亡者数の増加率は低下し, 増加は指数関数的ではなくなります. これは, 社会的接触の制限によるものです. COVID-19 の再生産数を制限する免疫症例の影響は, この段階ではまだ見られません.
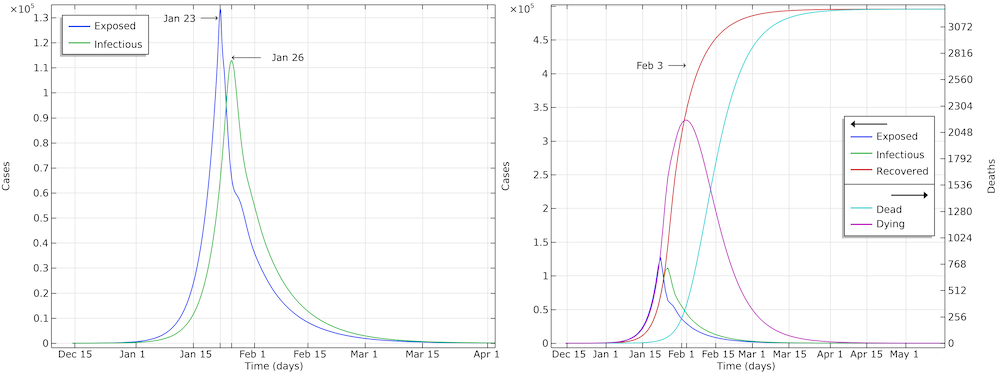
下のグラフは, 感染者数, 感染者数, 回復者数, 死亡者数における流行の進展を示しています. 対策が実施された1月23日, 感染者数が最大となった1月26日正午, および重篤な状態にある人が最大となった2月3日に, 追加のグリッド線を挿入しました. 回復した症例数は, もはや感染力がなくなり回復している症例を指すことに注意してください. 病院では, そのような患者は1週間から2週間後まで退院しないことになっていました.
湖北省での流行の進行. 時間の経過とともに予測される感染者数は50万人近くで, 報告された確定症例数の7倍以上です.
回復した症例をさらに見てみると, 流行から90日後にウイルスに感染しているか感染していた人が50万人近くになるとモデルが予測していることがわかります. これは確定症例数の7倍以上です. これは他の調査とも一致しており, 武漢の感染者のうち登録されたのはわずか 15% 程度 (文献 6, “Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2)“) であり, 感染者の多くは症状を報告していないか, COVID-19 の検査を受けてません.
湖北省のデータに対するパラメーター推定から得られた基本再生産数は 3.03 で, これは WHO の報告よりも高いが, 他の研究で報告された範囲内である (文献 7, “The reproductive number of COVID-19 is higher compared to SARS coronavirus“). 社会的距離の確保により, 再生産数は約 0.56 まで低下しましたが, これは死亡曲線に当てはめて得られた値です. この数値は他の場所で報告されている数値よりも低いですが, 現地での流行が急速に終息したことと一致しています.
スウェーデン人は互いに距離を保つ
スウェーデンは湖北省や他のほとんどの国とは異なる戦略を選択しました. 社会的交流には制限がありますが, 湖北省で実施されたような完全なロックダウンからは程遠いものでした. そのため, モデル化は湖北省の場合とは少し異なります. また, 最初の感染者と感染者がイタリアとオーストリアから輸入されたためでもあります. 冬休みに関連した入国者の分布を使用しました. 冬休みは国内のさまざまな地域で3週間にわたって分布しています. ただし, 旅行者の大半は, ストックホルム地域の住民が帰宅した2月17日から3月1日までの2週間に, 指数関数的に拡大するイタリアの流行にさらされた可能性があります.
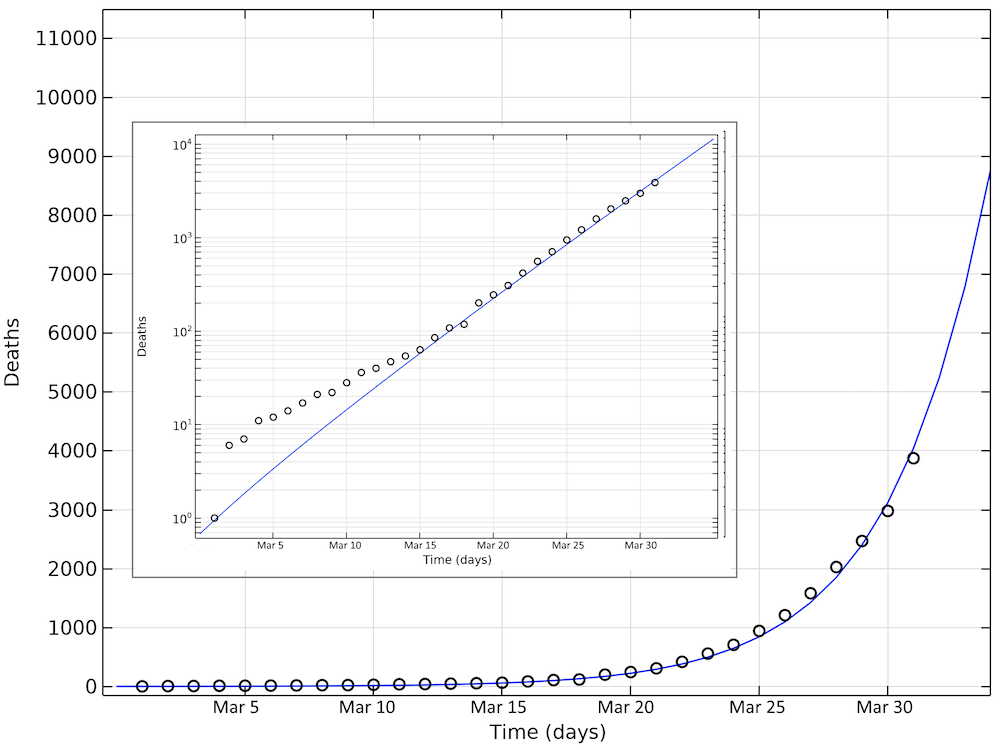
以下は, 報告された死亡者数と比較したシミュレーションによる死亡者数です. 4月2日も症例の増加は指数関数的です (対数グラフでは線形).
スウェーデンにおける COVID-19 による死亡者数. 33日目に最後に報告された値は4月2日に対応します. 小さい方のグラフは, 同じデータを対数スケールで y 軸に表示しています.
スウェーデンのデータに対するパラメーター推定から得られた基本再生産数は 2.95 で, 湖北省で得られた値 (3.03) と一致しています. 輸入症例の総数は約500件と推定されています.
社会的交流の制限は3月16日頃から実施されていますが, そのほとんどは推奨事項の形で実施されており, すぐに効果が出る可能性は低いため, 死亡者数にはまだ影響が見られません. このモデルでは, 制限が3月20日に完全に実施されたと想定しました.
2つのシナリオを想定してみましょう. 1つ目のシナリオでは, 社会的交流の減少が係数 0.35 で減少し, 2つ目のシナリオでは, この減少が係数 0.30 です. 最初のケースでは, 再生産数が 1.03 に減少します. つまり, 感染者1人あたり平均 1.03 人に感染します. 2番目のケースでは, 再生産数が 0.88 に減少します. これは1を下回り, 感染者10人のうち, 回復する前に “入れ替わる” ことができるのは (平均して) ほぼ9人だけであることを意味します.
どちらの場合も, 減少は湖北省の制限ほど劇的ではありませんが, これはスウェーデンが完全なロックダウンを実施していないため, 妥当な想定です.
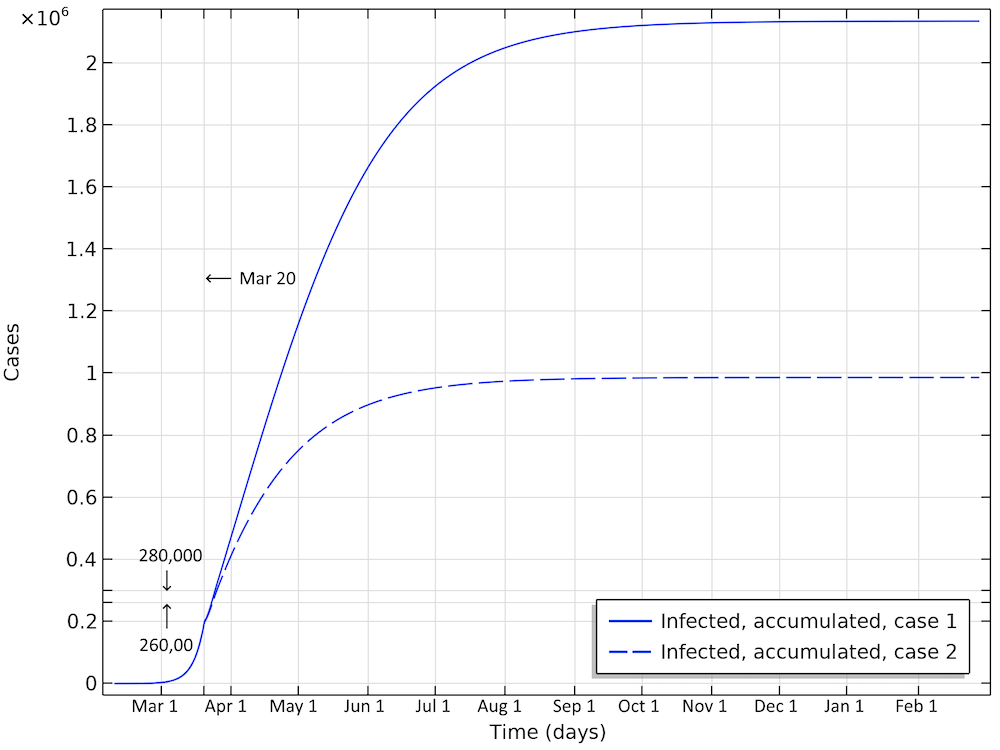
最初のシナリオでは, 約210万人が感染しており, これは人口の約 20% に相当します (下の図を参照). 4月2日時点で感染している, または感染したことのある人の数は28万人で, 確認された症例のほぼ60倍になります. 2番目のケースのシナリオでは, 4月2日時点で約26万人が感染していますが, 流行の進行は大幅に遅くなり, 阻止されているため, 流行が終息する前に, ある時点でウイルスに感染した人は100万人弱になります.
スウェーデンの2つのケースのシナリオにおける感染者総数. これは, 流行の進行全体を通じて感染するすべての個人の合計です.
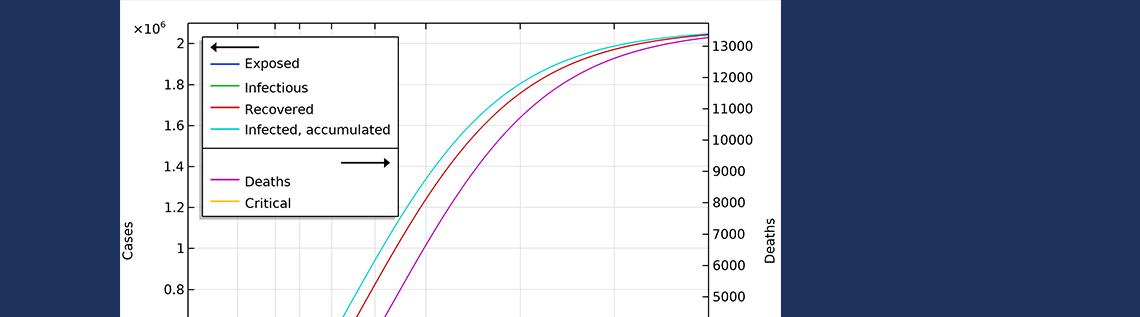
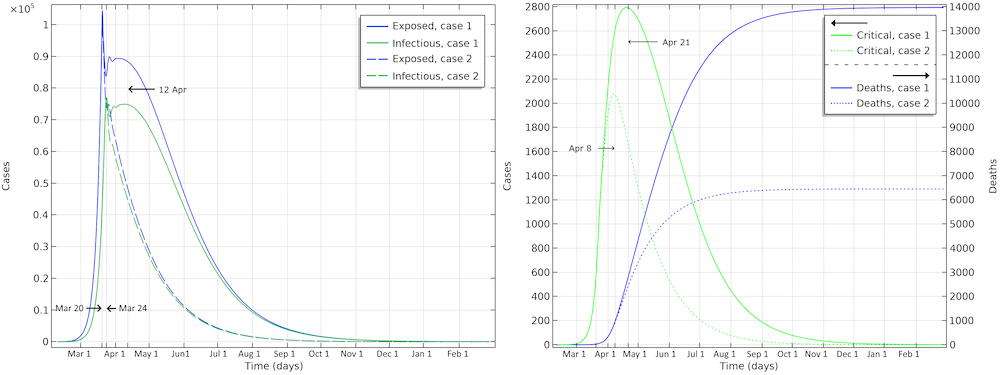
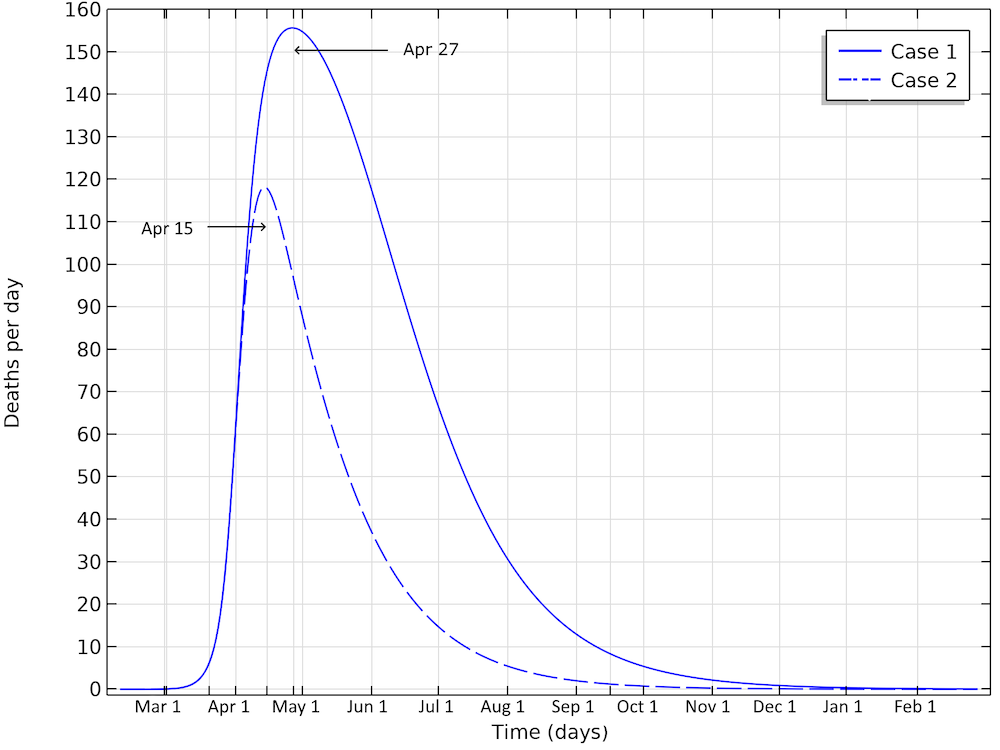
最初のシナリオでの最終的な死亡者数は13,000人以上です. また, 重症者数と1日の死亡者数のピークは4月21日に達し, 下の図に示すように, 1日あたりの死亡者数は155人でピークに達します. 2番目のシナリオでは, 死亡者数は約6,500人となり, 4月15日頃に死亡者数がピークに達し, 1日あたり約115人が死亡します.
3月12日から16日頃に実施された措置を考慮した, スウェーデンにおける流行の予測展開. 当局が講じた措置の効果は湖北省で講じられた措置よりも効率が低いと想定.
スウェーデンの死者数は, ケース1は4月27日頃, ケース2では4月15日頃にピークを迎えるでしょう.
再生産数を 1.03 から 0.88 に下げると, 社会的距離のわずかな違いで劇的な違いが生まれます. それでも, 流行が終息するまでにスウェーデンでは6500人近くが死亡することになります.
隔離された米国
私たちの小さな調査では, 感染者の数と米国への流入は, 海外からの感染者の分布を想定すると, 適切なパラメーターです. パラメーター推定は, 3月31日までの死亡データを使用して行われます. 米国特有の問題は, スウェーデンや湖北省と比較して, 流行の進行に地域差が大きいことと, 州によって異なる時期に異なる対策が取られていることです.
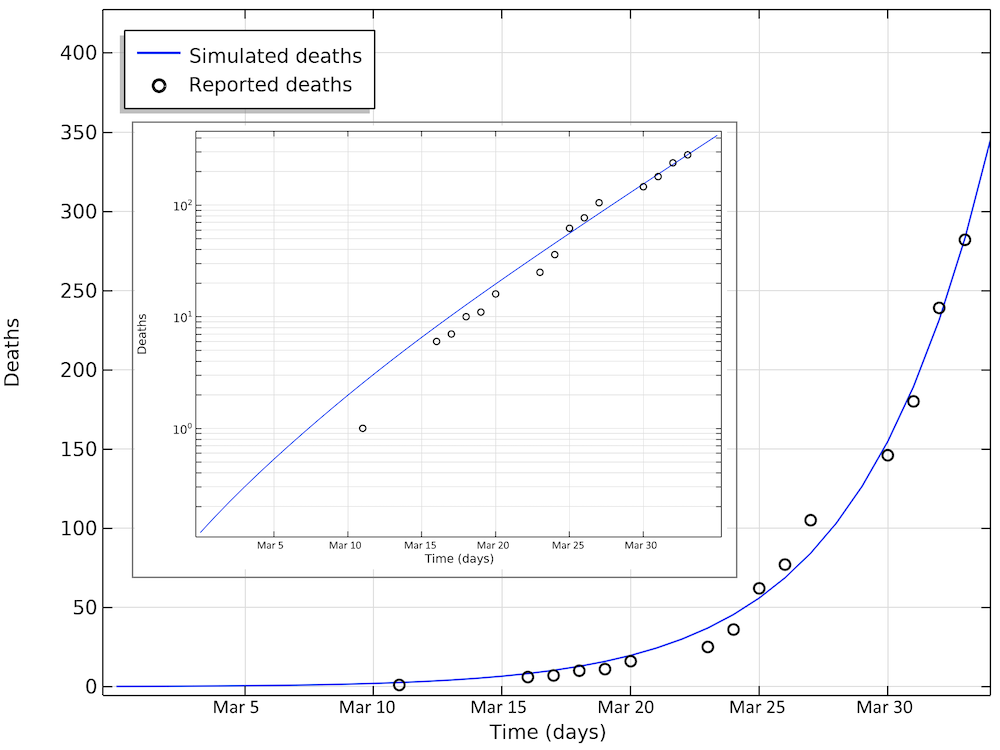
下の図は, グラフの31日目である3月31日時点でのシミュレーションによる死亡者数と報告された死亡者数を示しています. また, この場合, 対数グラフの線形増加に対応して, 死亡者数が指数関数的に増加していることがわかります.
3月31日時点の米国における死亡者数のシミュレーション値と報告値. 対数グラフでは, 死亡者数が小さい場合のモデルと報告された症例の偏差が, 大きい場合よりも大きくなっていることに注意してください. 小さい方のグラフは, 同じデータを対数スケールで y 軸に表示しています.
米国のデータに対するパラメーター推定から得られた基本再生産数は 2.97 で, スウェーデン (2.95) と湖北省 (3.03) に適合した値と一致しています. 輸入症例の総数は約8000件になります.
米国でも, 2つのシナリオを想定できます. 1つはスウェーデンの場合と同様に社会的交流を係数 0.3 で減らすシナリオ, もう1つは上記の湖北省の場合 0.185 まで交流レベルを下げるシナリオです. これも妥当です. 米国はスウェーデンと湖北省の中間の制限を課しているからです. つまり, 完全なロックダウンではなく, 社会的交流に関してスウェーデンよりも厳しい制限を課しています. この場合, 再生産数はそれぞれ 0.89 と 0.55 になります.
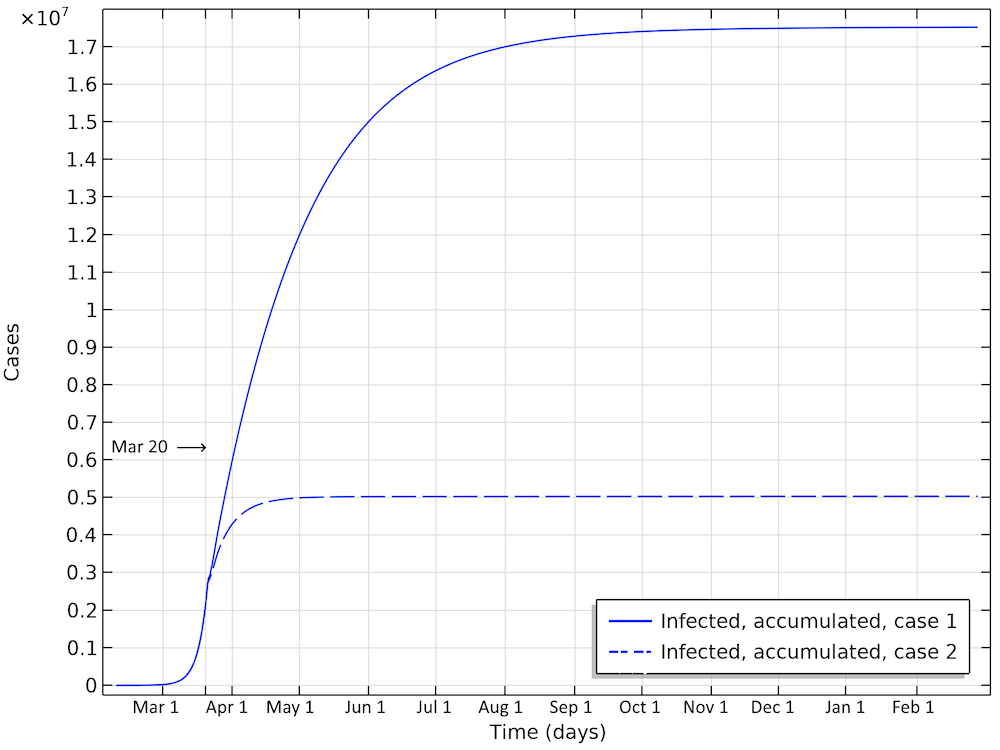
最初のシナリオでは, 流行が終息するまでに約2000万人のアメリカ人が感染すると予測されています (下の図を参照). 4月1日時点の感染者数は600万人になります. 2番目のケースでは, 約500万人が感染していることになります. これは, 報告された確認症例数の約25倍であり, 人口のごく一部しか検査されていないため, これも高い数字のように思えますが, あり得ない数字ではありません.
米国における2つのケースのシナリオでの累積感染者数. これは, 流行の進行全体を通じて感染するすべての個人の合計です.
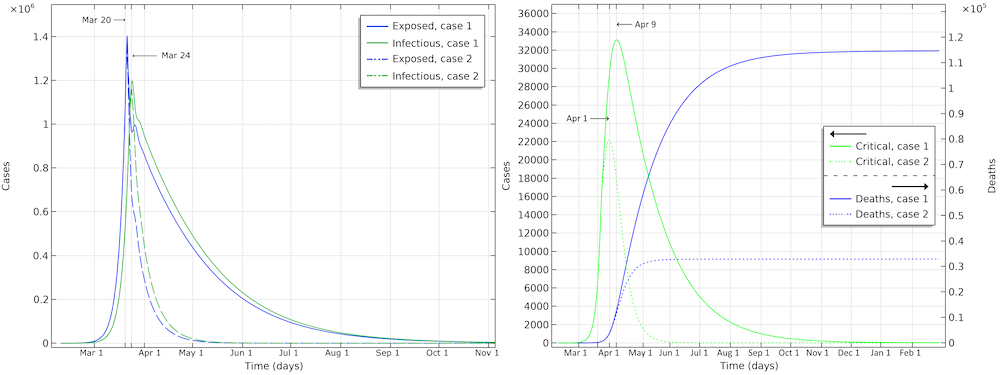
最初のシナリオでは, 米国の死者数は11万5000人になります (下図参照). 感染者数は3月24日ごろがピーク. 集中治療室の重症者数は4月9日がピーク. 湖北省と同じ制限を課す2番目のケースでは, 集中治療室の患者数は4月1日ごろがピーク. 流行が終息するまでの死者数は約3万3000人.
2つのケースのシナリオにおける曝露, 感染, 重篤, 死亡. 1つは再生産数が 0.89 まで減少した場合 (ケース1), もう1つは再生産数が 0.55 まで減少した場合 (ケース2).
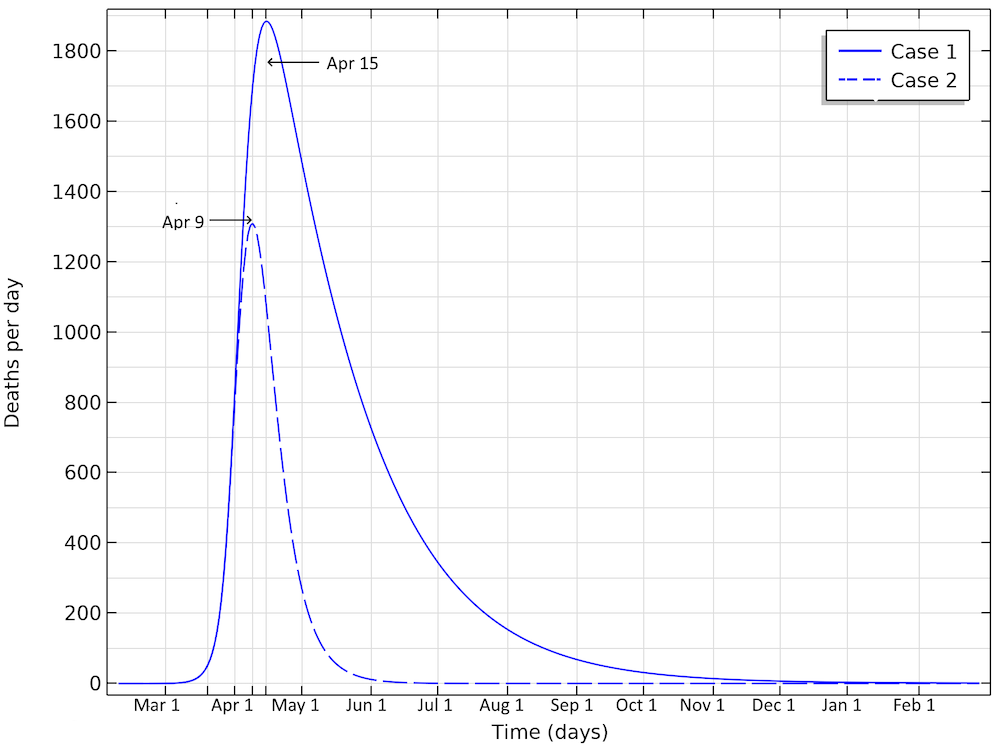
当社のモデルによると, 米国の死亡者数は, ケース1では4月15日頃, ケース2では4月9日頃にピークを迎えます.
1日あたりの死亡者数は, ケース1では4月15日頃, ケース2では4月9日頃にピークを迎えます. これは, 2つのケースでそれぞれ1日あたり1900人弱または1300人弱の死亡者に相当します. ケース1では, 1日あたりの死亡者数が多く, 期間がはるかに長いことがわかります. また, 数字は急速に悪化する可能性があります. 再生産数を 1.04 (係数 0.35) に下げると, つまり, 上記のケース1をわずかに上回ると, 流行が終息するまでに35万人の死者が出ることになります. モデルは, 流行中の1日あたりの重篤な状態にある人の数だけでなく, 流行が終息するまでの感染者総数も大幅に減少していることからも, 社会的距離戦略の影響が大きいことを明確に示しています.
新たな流行が発生したら何が起こるか?
厳しい制限を課して流行を迅速に鎮圧することの問題は, 人口が依然としてウイルスに対して非常に感受性が高いことです. 新たな感染例が発生した場合, 人口のごく一部のみが免疫を持ち, 流行は2回目の流行で再び指数関数的に拡大します. つまり, そのような社会は, 新たな流行に対して非常に迅速に行動を起こす準備ができていなければなりません. 制限を少なくすると, 最初の流行で死亡者数は多くなりますが, 人口の大部分が免疫を持つようになり, そのような人口は次の流行に対して脆弱ではなくなります. このような戦略を実施する場合, 高齢者など, 死亡率が高いリスクのある人口の一部を保護することが重要です. 2回目の流行では, これらの人々は免疫のある個人の緩衝材によって保護されます.
モデルの使用方法
ここで提示された結果は予測として解釈されるべきではありません. これらは現実を単純化したモデルからの結果です. 人口統計は考慮されていません. たとえば, 人口の年齢分布は, 病気の死亡率に大きな影響を与えます.
流行の進行が異なる段階にある研究対象国における地理的変動も, 正確に考慮されていません. 人々が国内のさまざまな地域間を移動する方法も, 流行の進行に影響を与えます.
さらに, 中国, スウェーデン, 米国の人々が取った行動がモデルへの入力に与える影響を予測することは非常に困難です. 中国疾病予防管理センター, スウェーデン公衆衛生局, 米国疾病予防管理センター (CDC) などの政府機関は, 年齢分布, 流行が発生した場所, 都市間の移動データ, 国内および国外への移動, その他の人口統計データを考慮した, より洗練されたモデルを持っています. また, さまざまな条件や年齢分布での潜伏期間や再生産数など, ウイルスや病気自体に関するより優れたデータも持っています.
しかし, ここで紹介したモデルを使用することは依然として興味深いことです. これらのモデルは, 流行のダイナミクスを理解するのに役立ちます. また, これらのモデルは, 社会的距離を保ち, 不必要な社会的交流を避けることで COVID-19 の再生産数を減らし, 集中治療室の感染患者のピークを減らし, 流行の全体的な影響を減らすことがいかに重要であるかについての直感も与えてくれます. さらに, Erlang-SEIR モデルは, 公衆衛生に携わる国内外の機関によって開発された都市や国向けのより洗練されたモデルの重要なコンポーネントおよび構成要素です.
モデルとアプリファイルをダウンロード
以下のボタンから, COVID-19 流行モデルの SEIR モデルとデモアプリケーションをダウンロードしてください.
参考文献
- H. Weiss, “The SIR model and the Foundations of Public Health”, MATerials MATemàtics, vol. 2013, no. 3, pp. 1–17, 2013.
- M. Höhle, “Flatten the COVID-19 curve”, Theory meets practice…, 2020.
- W.M. Getz and E.R. Dougherty, “Discrete Stochastic Analogs of Erlang Epidemic Models”, Journal of Biological Dynamics, vol. 12, pp.16–38, 2018.
- R. Verity, L.C. Okell, I. Dorigatti, P. Winskill, C. Whittaker, et al., “Estimates of the severity of coronavirus disease 2019: a model-based analysis”, The Lancet Infectious Diseases, 2020.
- A.J. Kucharski, T.W. Russell, C. Diamond, Y. Liu, J. Edmunds, S. Funk, R.M. Eggo, “Early dynamics of transmission and control of COVID-19: a mathematical modelling study”, The Lancet Infectious Diseases, 2020.
- R. Li, S. Pei, B. Chen, et at., “Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2)”, Science, 2020.
- Y. Liu, A.A. Gayle, A. Wilder-Smith, and J. Rocklöv, “The reproductive number of COVID-19 is higher compared to SARS coronavirus”, Journal of Travel Medicine, vol. 27, no. 2, 2020.
これは査読済みの出版物ではなく, 疫学者によって, または疫学者と協議して, 疫学基準に従って作成されたものではありません. さらに, 知られていないさまざまな状況が, 特に将来の進行に関して, ここで議論されているモデルの正確性に影響を与える可能性があります.



コメント (0)