
シュレディンガー・ポアソン方程式マルチフィジックスインターフェースは, 量子井戸, 量子ワイヤー, 量子ドットなどの量子閉じ込め電荷キャリアを持つ系をシミュレートします. ここでは, GaAs ナノワイヤーのベンチマークモデルを調べて, COMSOL Multiphysics® ソフトウェアのアドオン製品である半導体モジュールでこの機能を使用する方法を示します.
シュレディンガー・ポアソン方程式マルチフィジックインターフェース
COMSOL Multiphysics® バージョン 5.4 以降で利用可能なシュレディンガー・ポアソン方程式マルチフィジックスインターフェースは, 静電気インターフェースとシュレディンガー方程式インターフェースの間に双方向の連成を作成し, 量子閉じ込め系の電荷キャリアをモデル化します. 静電気からの電位は, シュレディンガー方程式の位置エネルギー項に寄与します. シュレディンガー方程式の固有状態からの確率密度の統計的に重み付けされた合計は, 静電気の空間電荷密度に寄与します. すべての空間次元 (1D, 1D軸対称, 2D, 2D軸対称, および 3D) がサポートされています.
シュレディンガー・ポアソン系の解法
シュレディンガー・ポアソン系は, 静電気に対して定常解析が必要であり, シュレディンガー方程式に対して固有値解析が必要であるという点で特殊です. 双方向結合系を解くには, シュレディンガー方程式とポアソン方程式を, 自己無撞着な解が得られるまで反復的に解きます. 反復手順は, 次の手順で構成されます:
ステップ 1
反復処理に適切な初期条件を与えるために, 電位 V についてポアソン方程式
(1)
を解きます. ここで, \epsilon は誘電率, \rho は空間電荷密度です.
この初期化ステップでは, \rho は物理的な議論から得られる最良の初期推定値によって与えられます. たとえば, トーマス・フェルミ近似を使用します.
ステップ 2
前のステップの電位 V は, シュレディンガー方程式の電位エネルギー項 V_e に寄与します
(2)
ここで, q はキャリア粒子の電荷で, 次式で与えられます
(3)
ここで, z_q は電荷数, e は電荷です.
ステップ 3
式 2で与えられた更新されたポテンシャルエネルギー項を使用して, シュレディンガー方程式を解き, 固有エネルギー E_i と, それに対応する正規化された波動関数 \Psi_i を生成します.
ステップ 4
粒子密度プロファイル n_\mathrm{sum} は, 確率密度の統計的に重み付けされた合計を使用して計算されます.
(4)
ここで, 重み N_i は, 面外連続状態のフェルミ・ディラク分布を積分することによって与えられます (したがって, モデルの空間次元に依存します).
(5)
(6)
(7)
ここで, g_i は縮退係数, E_fはフェルミ準位, k_B はボルツマン定数, T は絶対温度, m_d は状態密度有効質量, F_0 および F_{-1/2} はフェルミ・ディラク積分です.
簡単にするために 式 4 の加重合計では, 合計のインデックス i が1つだけ示されています. もちろん, 合計には複数のインデックスがある場合があります. たとえば, ここで説明するナノワイヤーモデルでは, 合計は方位量子数と固有エネルギーレベルの両方 (方位量子数ごとに) にわたって行われます.
ステップ 5
粒子密度プロファイル n_\mathrm{sum} が与えられたら, 空間電荷密度 \rho を再推定し, ポアソン方程式を再度解いて, 新しい電位プロファイル V を取得します. 新しい空間電荷密度の簡単な式
(8)
は, ほとんどの場合, 反復の発散につながります. はるかに優れた推定値は, 次の式で得られます
(9)
ここで, V_\mathrm{old} は, 前の反復からの電位であり, \alpha は追加の調整パラメーターです. 式 9は, ソルバーシーケンスによって空間電荷密度 \rho を計算するために使用されます.
この式は, 粒子密度 n_\mathrm{sum} が V_\mathrm{old} の結果であり, ポアソン方程式が再度解かれて新しい V が得られると変化するという観察に基づいています. 言い換えると, 式 8 は, より明示的に次のように記述できます.
(10)
これは, n_\mathrm{sum} が V_\mathrm{old} の結果であり, \rho はポアソン方程式を再度解いて新しい V を取得するために使用されるためです.
自己無頓着な解を得るには, 次の式の方がよいでしょう
(11)
この時点では, n_\mathrm{sum,new} は, 次の反復におけるシュレディンガー方程式の解から得られるため, 不明です. ただし, ボルツマン統計を使用して予測を立てることができます. ボルツマン統計は, ポテンシャルエネルギー V_e=qV と粒子密度 n_\mathrm{sum} の間に単純な指数関係を提供します.
(12)
これにより, \alpha=0 の場合の 式 9 が得られます. これは, ボルツマン統計が適切な近似値となる高温でうまく機能します. 低温では, \alpha を正の数に設定すると, 収束が加速されます.
ステップ 6
ポアソン方程式を再度解いて新しい電位プロファイル, V が得られたら, それを前回の反復の電位 V_\mathrm{old} と比較します. 2つのプロファイルが目的の許容範囲内で一致する場合, 自己無頓着性が達成されます. それ以外の場合は, ステップ 2 に進み, 反復を続行します.
専用のシュレディンガー・ポアソンスタディタイプを使用すると, ソルバーシーケンスで上記の手順を自動的に生成できます.
ベンチマークの例: ナノワイヤーモデル
GaAs ナノワイヤーチュートリアルモデルは, J.H. Luscombe, A.M. Bouchard, および M. Luban による “量子ナノ構造における電子閉じ込め: 自己無撞着ポアソン・シュレディンガー理論” という論文に基づいています.
無限の長さと円筒対称性を前提として, 1D軸対称空間次元を選択します. 次に, 半導体ブランチのシュレディンガー・ポアソン方程式マルチフィジックスインターフェースを選択します. これにより, モデルビルダーに, シュレディンガー・ポアソンマルチフィジックスカップリングとともに, シュレディンガー方程式および静電気インターフェースが追加されます.
ナノワイヤーモデルのシュレディンガー・ポアソン方程式インターフェースを選択します.
論文の説明に従って, ナノワイヤーの半径は 50 nm に設定されています. 電子有効質量は自由電子質量の 0.067 倍に設定され (論文のフェルミ温度の結果で示唆されているように), 誘電率は 12.9 と想定されています. モデルのフェルミエネルギーレベルは 0 V に設定され, 壁の電位は研究者によって説明されているフェルミレベル固定境界条件と一致するように -0.7 V に設定されています. 論文の図2および3と比較するために, 温度 10 K で 2·1018 cm–3 の均一なイオン化ドーパントの場合をモデル化します. 上記の数値は, モデルのグローバルパラメーターとして入力されます.
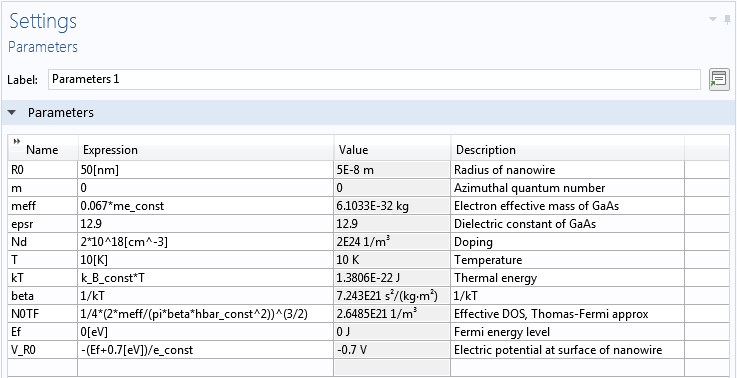
ナノワイヤーモデルのグローバルパラメーター.
論文のアプローチに従って, まずトーマス・フェルミ近似解を解き, それを完全連成シュレディンガー・ポアソン方程式の初期条件として使用します. トーマス・フェルミ近似の式は, モデル内のローカル変数として入力されます.
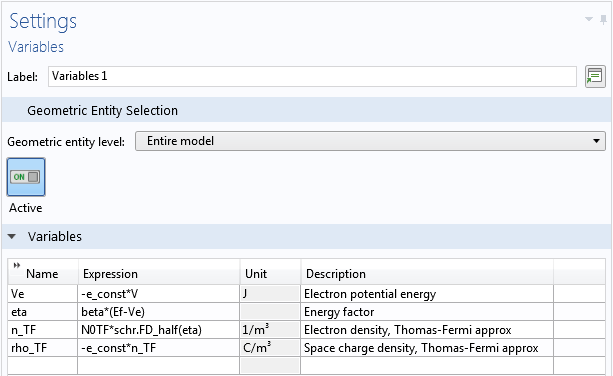
ナノワイヤーモデルのローカル変数.
グローバルパラメーターとローカル変数が定義されているので, モデルビルダーのジオメトリ, 材料, フィジックスノードのさまざまな入力フィールドにそれらを使用して簡単に入力できます. いくつか注意すべき点があります:
- 方位角量子数 m は, 前述のとおり, その値をスイープして合計できるようにパラメーター化されており, シュレディンガー方程式フィジックスノードの設定ウィンドウに入力されています
- 以前のブログの超格子のバンドギャップの計算で, 固有値スケール λscale が, 固有エネルギー E_i (E_i = λscale を生成するための無次元固有値 λ の乗算係数として機能することを思い出してください.)
- たとえば, λscale が 1 eV の場合, 固有値が 1.23 であれば, 固有エネルギーは 1.23 eV であることを示します
- 静電気インターフェースでは, 前述のように, ナノワイヤーの壁の値を設定するために, 電位境界条件が追加されます
- さらに, 2つの空間電荷密度ドメイン条件が追加されます. 1つはイオン化ドーパント用, もう1つは トーマス・フェルミ 近似用です (後者はシュレディンガー・ポアソンスタディではオフにする必要があります)
シュレディンガー・ポアソンマルチフィジックスカップリングの設定
シュレディンガー・ポアソンカップリングマルチフィジックスノードの設定ウィンドウで, 方程式セクションを展開して, このノードに実装されている方程式を確認します. 上記のシュレディンガー・ポアソン系の求解セクションを読んでいれば, 見覚えがあるはずです. 設定のカップリングインターフェースセクションでは, 2つのカップリングフィジックスインターフェースを選択できます. モデル入力セクションでは, 以下のスクリーンショットに示すように, 系の温度を設定します:
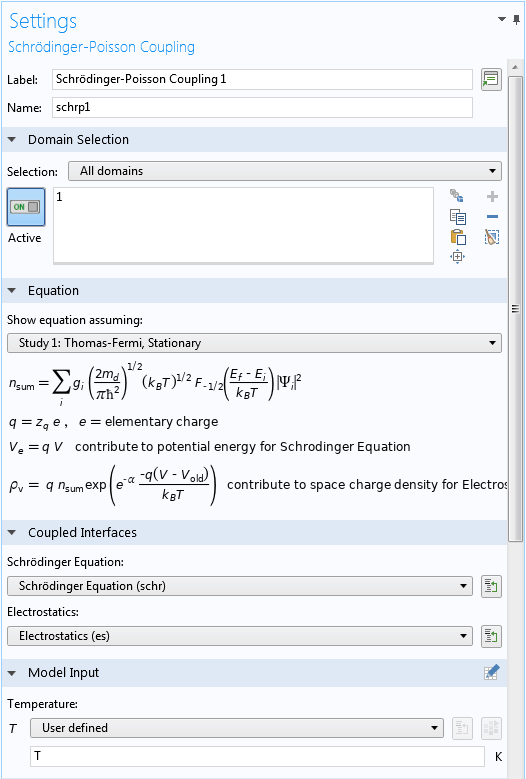
シュレディンガー・ポアソンカップリングノード の設定ウィンドウの上部
粒子密度計算セクション (下のスクリーンショット) では, 式 4 で説明されているように, 確率密度の統計的に重み付けされた合計を指定します. フェルミ・ディラク統計, 放物線バンドのデフォルトオプションが選択されている場合は, 式 5 ~ 式 7 を使用して重み N_i が計算されます. 重みに異なる式を入力するためのユーザー定義オプションも利用できます.
縮退した方位量子数のペア (m = ±1, ±2 など) を考慮するために, 縮退係数 g_i に式 1+(m>0) を使用します. これは, m = 0 の場合は 1, m > 0 の場合は 2 と評価されます.
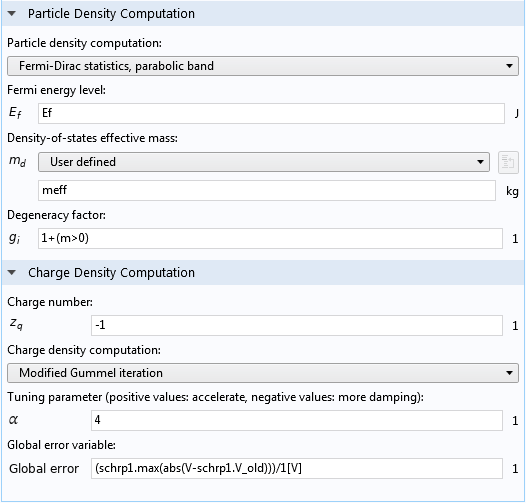
シュレディンガー・ポアソンカップリングノードの設定ウィンドウの下部.
電荷密度計算セクション (上のスクリーンショット) は, 式 3 の電荷数, z_q の入力を受け取ります. 修正 Gummel 反復のデフォルトオプションが選択されている場合は, 式 9 を使用して新しい空間電荷密度, \rho を計算します. 独自の数式を入力できるユーザー定義オプションなど, その他のオプションも利用できます.
グローバルエラー変数の既定の式 (schrp1.max(abs(V-schrp1.V_old)))/1[V] は, 最新の2回の反復からの電位場間の最大差を V 単位で計算します. 前置名 schrp1 はシュレディンガー・ポアソンカップリングノードの名前入力フィールドと一致し, 変数名 V は静電気インターフェースの従属変数名と一致している必要があることに注意してください. これらの名前は, より複雑なモデルでは既定の名前から変更される可能性があり, 名前が一致しない場合は式が黄色に変わります. この場合, 手動で編集する必要があります.
シュレディンガー・ポアソンスタディステップの設定
スタディ2の専用のシュレディンガー・ポアソンスタディステップは, ソルバーシーケンスで自己無撞着反復を自動的に生成します. 反復スキームは, 上記のシュレディンガー・ポアソン系の求解で概説されています.
まったく新しい問題を扱っている場合は, スタディ設定セクションの固有周波数検索方法メニューで, 固有エネルギーの範囲を見つけるためにデフォルトの手動検索オプションを使用する必要があることがよくあります. 範囲が見つかったら, 範囲と固有値の数を適切に設定した領域検索オプションに切り替えて, すべての重要な固有状態がソルバーによって確実に見つかるようにすることができます. このチュートリアルでは, 推定エネルギー範囲は -0.15 ~ 0.05 eV です. これは, 前述したように, 単位のない固有値の -0.15 ~ 0.05 に相当します.
入力フィールドの実数部と虚数部は, それぞれ固有値の実数部と虚数部を指します. 束縛状態の固有エネルギーを探すために, 実数部の入力フィールドを予想されるエネルギー範囲に設定し, 虚数部の入力フィールドを0付近の小さな範囲に設定して, 数値ノイズまたはわずかに漏れのある準束縛状態を捕獲します (以下を参照):
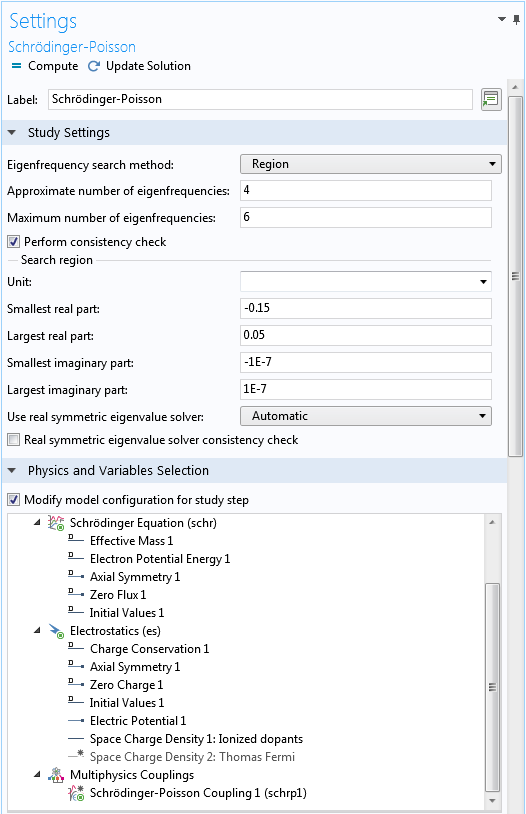
シュレディンガー・ポアソンスタディステップの設定ウィンドウの上部
前に述べたように, 2番目の空間電荷密度ドメイン条件は, スタディ1のトーマス・フェルミ近似解にのみ使用されます. したがって, 上のスクリーンショットに示すように, フィジックスと変数の選択セクションでは無効になっています.
反復セクションの終了方法ドロップダウンメニューの既定のオプションはグローバル変数の最小化です. これにより, 解プロセス中の各反復の後に, グローバルエラー変数の履歴を表示する結果テーブルが自動的に更新されます. 組み込みのグローバルエラー変数 schrp1.global_err は, シュレディンガー・ポアソンカップリングマルチフィジックスノードで既に設定されているように, 最新の2回の反復からの電位場間の最大差を V 単位で計算します. (前置名 schrp1 は, シュレディンガー・ポアソンカップリングノードの名前入力フィールドと一致する必要があることに注意してください. ) したがって, 許容値を 1E-6 に設定すると, 最大差が 1 uV 未満になると反復が終了することを意味します. これらの設定については, 以下のスクリーンショットを参照してください:
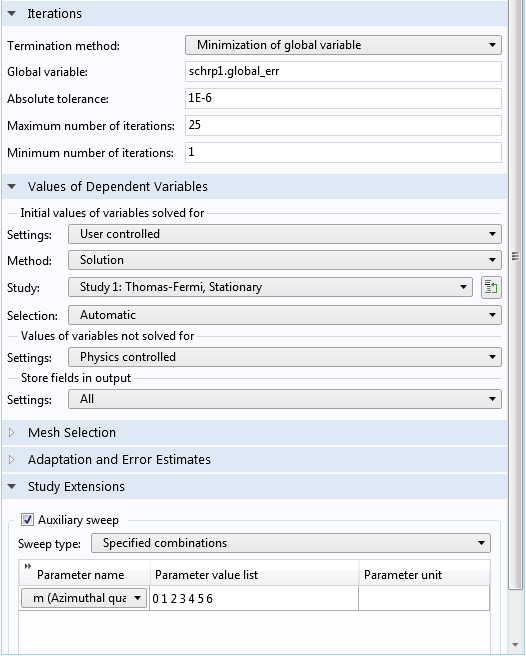
シュレディンガー・ポアソンスタディステップの設定ウィンドウの下部.
従属変数の値セクションでは, スタディ1のトーマス・フェルミ近似解をこのスタディの初期条件として選択します. 次に, 補助スイープ機能を使用して, 非負の方位量子数 m のリストを求めます. 負の数は, 前述のとおり, 縮退係数 g_i の式 1+(m>0) を使用して考慮されます. 専用のソルバーシーケンスは, すべての固有状態の確率密度の統計的に重み付けされた合計を自動的に実行します.
自己無頓着性の結果の検証
ソルバーは, トーマス・フェルミ近似によって提供される良好な初期条件と, 式 9 によって与えられる空間電荷密度の良好な前方推定値のおかげで, 8回の反復で収束します.
電子密度, ポテンシャルエネルギー, および部分軌道寄与のプロットは, 参考文献で公開されている図とよく一致しています.
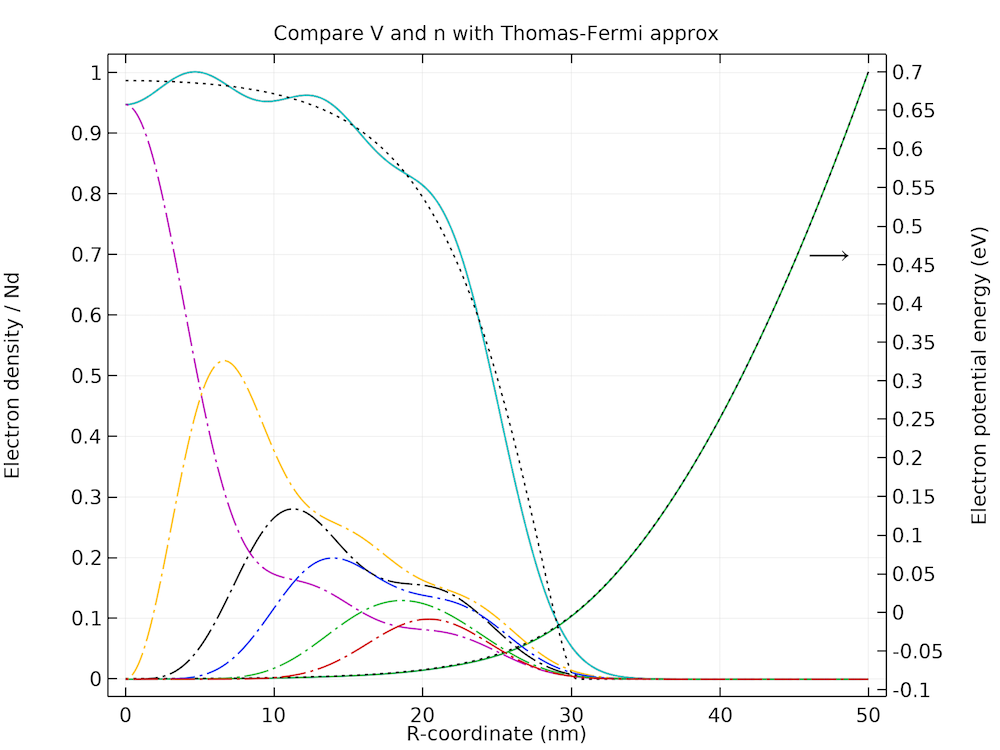
電子密度, 位置エネルギー, および部分軌道寄与と参考論文で公開された図との比較.
下のグラフは, 電子密度と位置エネルギーの両方のプロファイルに存在するフリーデル型の空間振動を示しています.
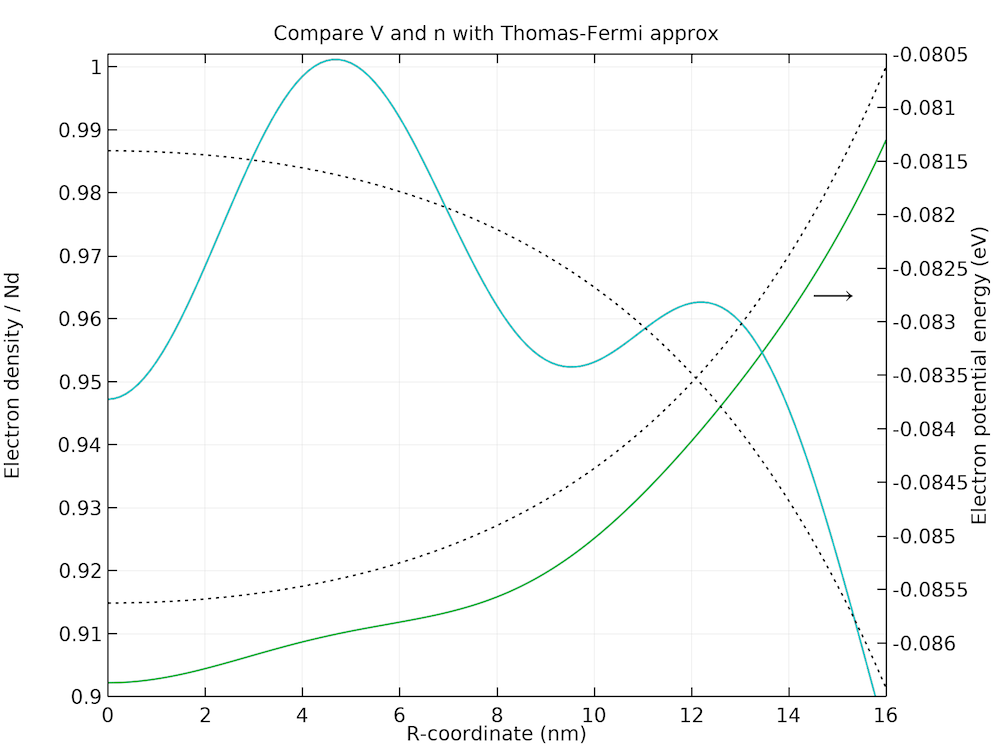
電子密度とポテンシャルエネルギープロファイルにおける Friedel 型空間振動の拡大プロット.
次のステップ
このブログでは, シュレディンガー・ポアソン方程式インターフェースと, シュレディンガー・ポアソンスタディタイプを使用すると, GaAs ナノワイヤーの自己無撞着シュレディンガー・ポアソン結果ベンチマークモデルを例として, シュレディンガー・ポアソン系を簡単に設定して解くことができることを説明しました. このモデルを自分で試すには, 下のボタンをクリックしてアプリケーションギャラリに移動し, このチュートリアルの説明書と MPH ファイルをダウンロードしてください.
参考文献
- J.H. Luscombe, A.M. Bouchard, and M. Luban, “Electron confinement in quantum nanostructures: Self-consistent Poisson-Schrödinger theory,” Phys. Rev. B, vol. 46, no. 16, p. 10262, 1992.



コメント (0)