COMSOL Multiphysics® ソフトウェアのバージョン 5.6 以降, 半導体モジュールでは, シュレーディンガー方程式フィジックスインターフェースに多成分波動関数を処理する機能が導入されました. 前回のブログでの説明に続き, 均一な磁場内のシリコン量子ドットのモデルを例として, この機能について引き続き検討します.
量子ドットとは
量子ドットはナノテクノロジーに不可欠な要素であり, 太陽電池, LED, ディスプレイ, 光検出器, 量子コンピューティングへの応用が期待されています. 最後の応用分野に関する論文の 1 つは, スピン軌道量子ビットをテーマにした Jock ら (参考文献 1) によって発表されています. この論文の補足ノート 1 で, 著者らは均一な磁場内のシリコン量子ドットを表す定式化を示し, 補足図 1 に数値解を示しました. この数値解は, このモデルによって再現されます.
定式化
参考文献 1の補足注1の式1は, スピン軌道相互作用を含まない均一磁場\mathbf{B}内のシリコン量子ドットの単一電子ハミルトニアンを与えます:
(1)
+\frac{P_y^2}{2 m_\perp}
+\frac{P_z^2}{2 m_\parallel}
+V(\mathbf{r})
+\mu_B \mathbf{B} \cdot \sigma
ここで, m_\perp と m_\parallel はそれぞれ横方向と縦方向の有効質量です. V は量子ドットの閉じ込めポテンシャルエネルギーです. \mu_B はボーア磁子です. \mathbf{\sigma} はパウリ行列のベクトルです. 磁気回転比テンソルは, 論文に従って値 2 のスカラーであると仮定されます. そして, 運動量 \mathbf{P}は
(2)
によって与えられます.
ここで, e は素電荷, \mathbf{A} は, \mathbf{A}(\mathbf{r})=\frac{1}{2}\mathbf{B}\times\mathbf{r} で与えられるベクトルポテンシャル. COMSOL Multiphysics® の全てのフィジックスインターフェースでは, exp(i k x – i \omega t) ではなく, exp(-i k x + i \omega t) という工学の符号規約を採用しているので, 虚数単位 iの前の符号にはマイナス記号はありません.
閉じ込めポテンシャルエネルギー項V(\mathbf{r})は, 次の論文中の式9で与えられます:
(3)
+\frac{1}{2} m_\perp \omega_y^2 y^2
+q F_z z
+U_0 \Theta(z)
ここで, 最初の 2 つの項は, 横方向の異方性調和トラッピングポテンシャルを表し, トラップ角周波数は x 方向と y 方向でそれぞれ \omega_x と \omega_y です. 3 番目の項は z 方向の電場 F_z を表します. q は粒子の電荷です (電子の場合は q=-e). 最後の項は, z = 0 のシリコン酸化物界面における高さ U_0 の電位障壁です.
パラメーターと変数
モデリングパラメーターは以下の表の通りです:
|
名前 |
式 |
値 |
説明 |
|---|---|---|---|
|
mxy |
0.19*me_const |
1.7308E-31 kg |
横有効質量 |
|
mz |
0.98*me_const |
8.9272E-31 kg |
垂直有効質量 |
|
wx |
1[meV]/hbar_const |
1.5193E12 rad/s |
x 方向のトラップ周波数 |
|
wy |
3*wx |
4.5578E12 rad/s |
y 方向のトラップ周波数 |
|
Fz |
10[MV/m] |
1E7 V/m |
電場 |
|
U0 |
3[eV] |
4.8065E-19 J |
酸化エネルギー障壁 |
|
uB |
e_const*hbar_const/2/me_const |
9.274E-24 m2·A |
ボーア磁子 |
|
B |
1[T] |
1 T |
磁束密度 |
磁場を除くすべてのパラメーターは論文に記載されており, 磁場については推定値 1[T] が使用されています.
ベクトルポテンシャル\mathbf{A}(\mathbf{r})=\frac{1}{2}\mathbf{B}\times\mathbf{r}は, 均一な磁場がy方向を指していると仮定して, 変数を使用して指定されます:
|
名前 |
式 |
単位 |
説明 |
|---|---|---|---|
|
Ax |
z*B/2 |
Wb/m |
ベクトルポテンシャル |
|
Ay |
0[Wb/m] |
Wb/m |
ベクトルポテンシャル |
|
Az |
-x*B/2 |
Wb/m |
ベクトルポテンシャル |
フィジックス設定
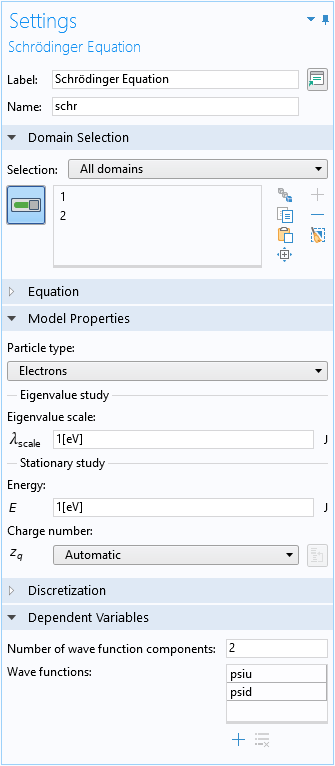
シュレーディンガー方程式フィジックスインターフェースは, スピンアップとスピンダウンの2つの波動関数成分, psiuと psidで設定されています:
デフォルトの 有効質量 ドメイン条件は, 横方向と垂直方向の有効質量を指定するために使用されます:
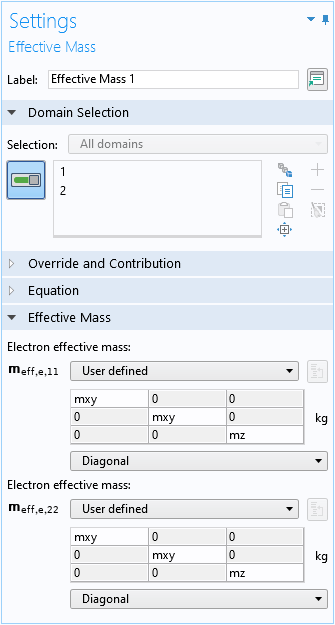
このモデルでは, 2 つの波動関数成分が同じ有効質量を共有していますが, 一般的なケースでは, ユーザーインターフェースによって, 異なる波動関数成分に異なる値が許可されます.
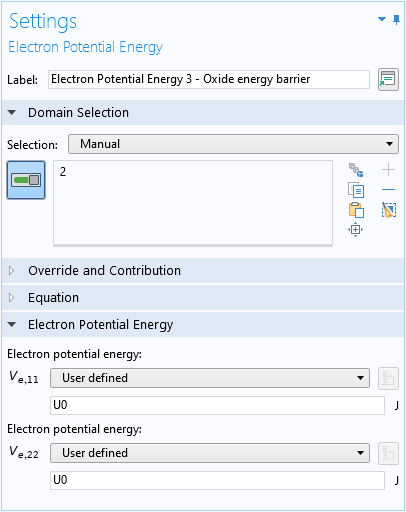
3つの電子ポテンシャルエネルギー領域条件は, 横方向調和トラッピングの閉じ込めポテンシャルエネルギー項V(\mathbf{r}) (式3)を設定するために使用されます:
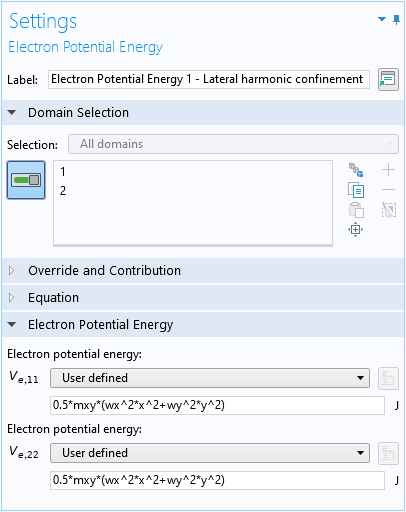
電場に関して:
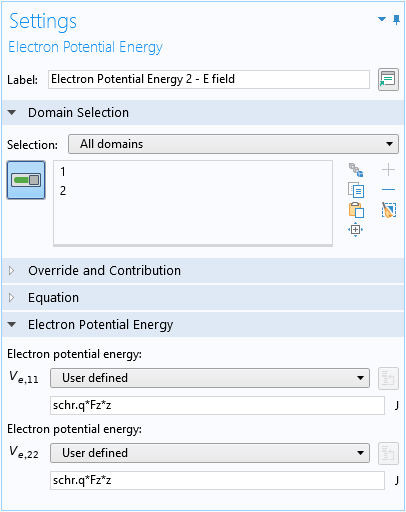
酸化障壁:
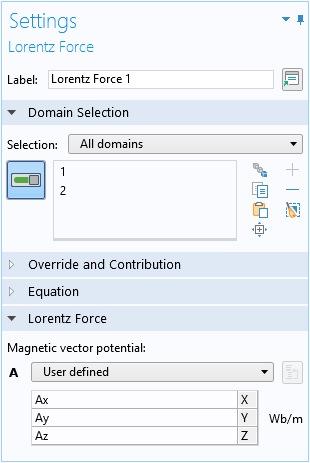
ベクトルポテンシャルからの運動量への寄与(式2の2番目の項)は, ローレンツ力ドメイン条件を使用して実装されます:
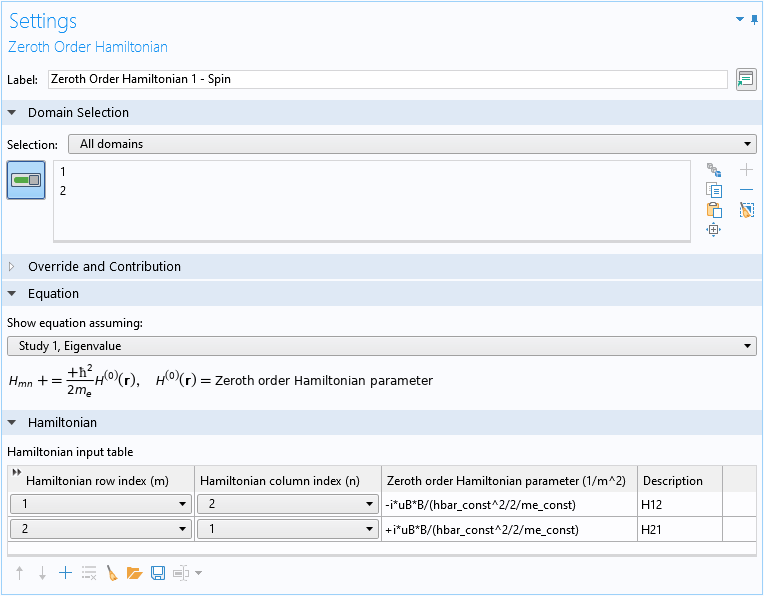
最後に, スピンアップ成分とスピンダウン成分の磁気結合(式1の最後の項)は, ゼロ次ハミルトニアン領域条件で実装されます:
ドメイン条件によって想定される係数 \hbar^2/2m_e は入力で補正される必要があることに注意してください. その結果, 最終的な結果は 式 1 の最後の項になります:
(4)
= \mu_B B \, \mathbf{n}_y \cdot \mathbf{\sigma}
= \mu_B B \sigma_y
= \left( \begin{array}{cc}
0 & -i\, \mu_B B \\
+i\, \mu_B B & 0 \end{array} \right)
上記の”ゼロ次ハミルトニアン”ドメイン条件の設定ウィンドウのスクリーンショットでは, ”ハミルトニアン入力テーブル”の最初の行は”式 4”の行列の (1,2) 要素を実装し, ”2 行目”は (2,1) 要素を実装しています.
単純なスイープメッシュが作成され, 固有値スタディを使用して最初のいくつかの固有状態が検索されます.
結果の考察
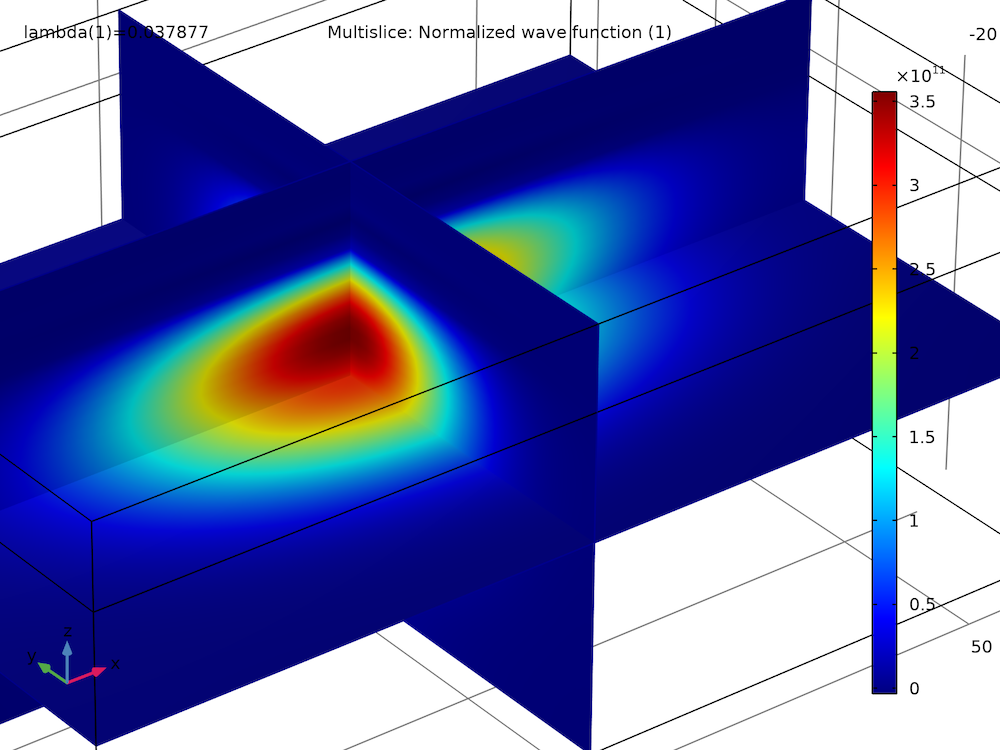
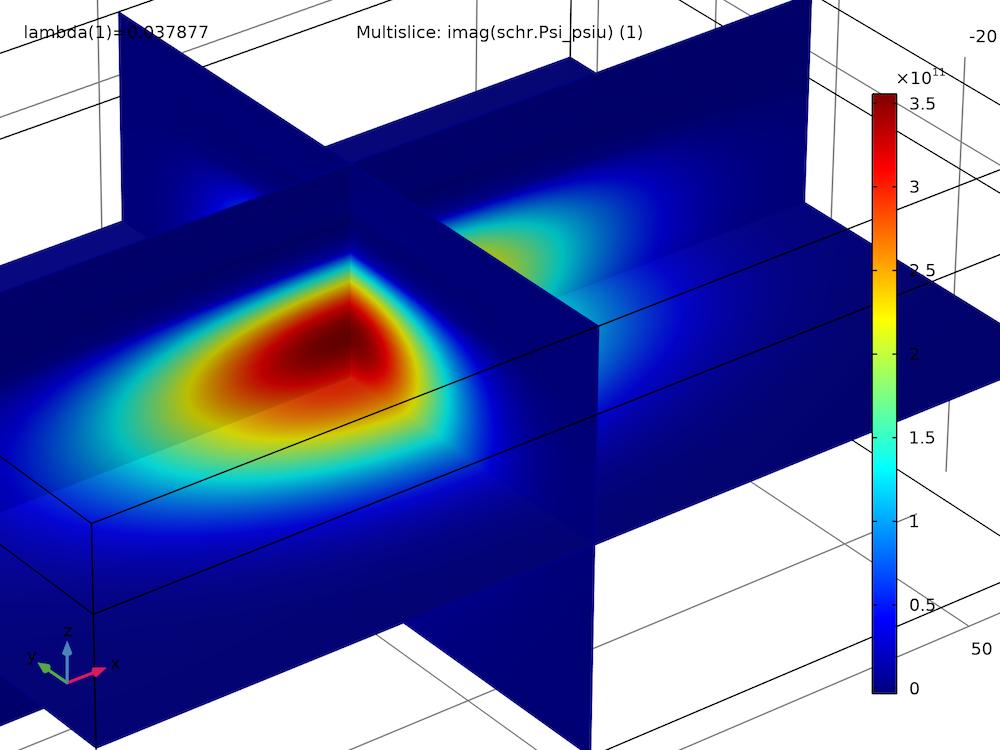
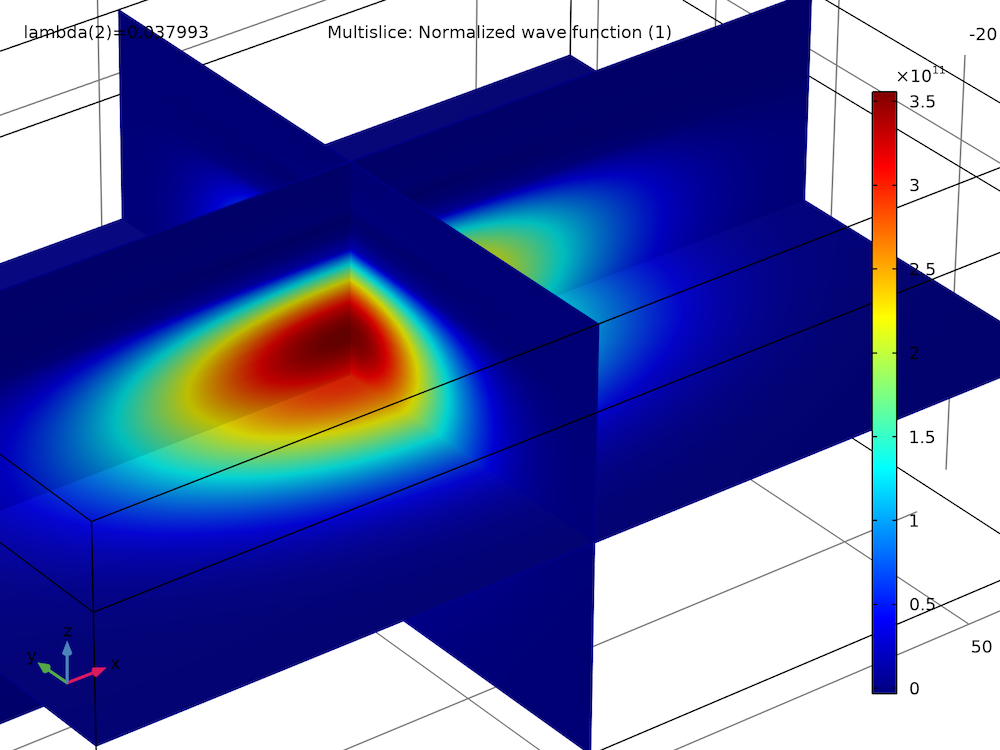
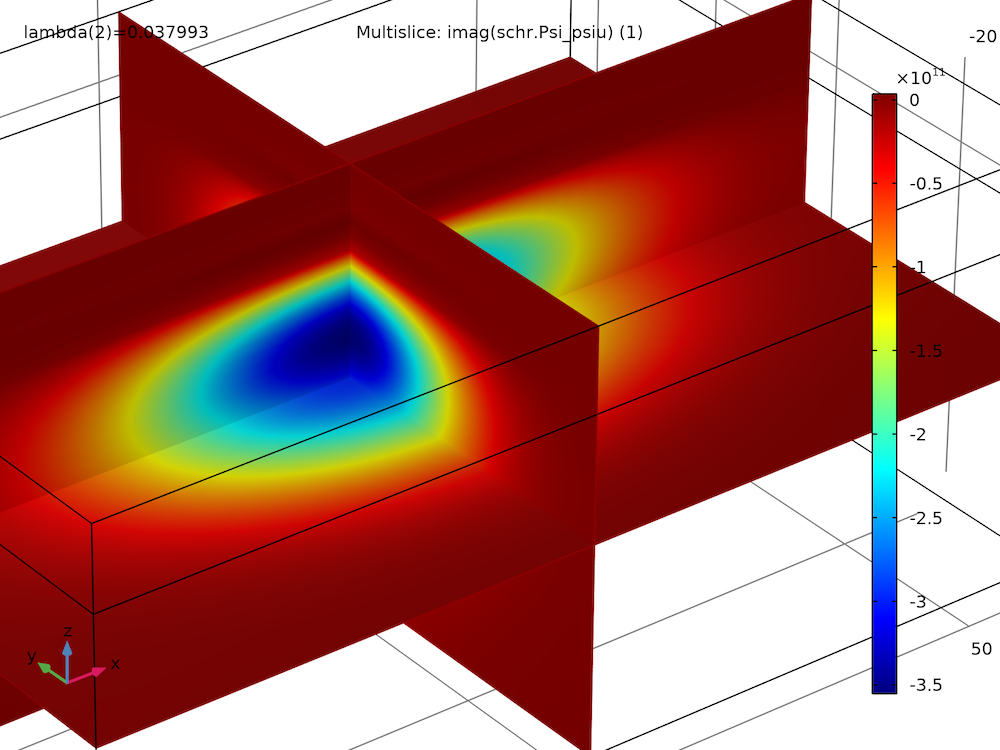
最初の2つの固有状態のスピンアップ波動関数成分の実部と虚部をプロットすると, いくつかの符号反転を除いて, それらは同様の大きさと形状を持っていることがわかります:
|
スピンアップ波動関数成分 |
|
|---|---|
|
|
|
|
基底状態, 実部 |
基底状態, 虚部 |
|
|
|
|
第一励起状態, 実部 |
第一励起状態, 虚部 |
スピンダウン波動関数の成分にも, スピンアップ成分と比較して, またそれら自身においてもこの傾向があります.
この観察を理解するために, ピーク密度点付近の波動関数成分を評価します:
|
固有値 |
up (1), Point: (0, 0, -2) |
down (1), Point: (0, 0, -2) |
|---|---|---|
|
0.03788 |
1.000+1.000i |
1.000-1.000i |
|
0.03799 |
1.000-1.000i |
1.000+1.000i |
基底状態(上記の結果表の最初の行)では, 全体のスケーリング係数が約 3.6e11 まで, スピンアップ成分の振幅は 1+i=(1)(1+i), スピンダウン成分の振幅は 1-i=(-i)(1+i) であることがわかります. したがって, 2 つの成分によって形成されるベクトルは \left(\begin{array}{c}1\\-i\end{array}\right) に比例し, これは y スピン演算子 S_y のスピンダウン固有状態として認識されます. これは, 磁場内の電子の低エネルギー状態ではスピン磁気モーメントが磁場と平行であり, したがってスピンは磁場と反平行であるという直感的な図と一致しています.
同様に, 最初の励起状態については, 全体のスケーリング係数が約 3.6e11 まで, スピンアップ成分の振幅は 1-i=(1)(1-i) で, スピンダウン成分の振幅は 1+i=(+i)(1-i) です. したがって, 2 つの成分によって形成されるベクトルは \left(\begin{array}{c}1\\+i\end{array}\right) に比例し, これは y スピン演算子 S_y のスピンアップ固有状態として認識されます. これは, 磁場内の電子の高エネルギー状態は, スピン磁気モーメントが磁場と反平行であり, したがってスピンが磁場と平行であるという直感的な図と一致しています.
この観察結果は, 計算された2つの固有状態間のエネルギー差を, 均一磁場(2\, \mu_B B)内のスピンアップ電子とスピンダウン電子間の予想されるエネルギー差と比較することで, さらに確認することができます:
|
固有値 |
計算されたエネルギー差 (meV) |
正しいエネルギー差 (meV) |
|---|---|---|
|
0.03788 |
0.1158 |
0.1158 |
最初の 2 つの固有状態間の計算されたエネルギー差と正しいエネルギー差は非常によく一致しており, 両方とも 0.116 meV という同じ値に評価されます.
確率密度と運動量密度
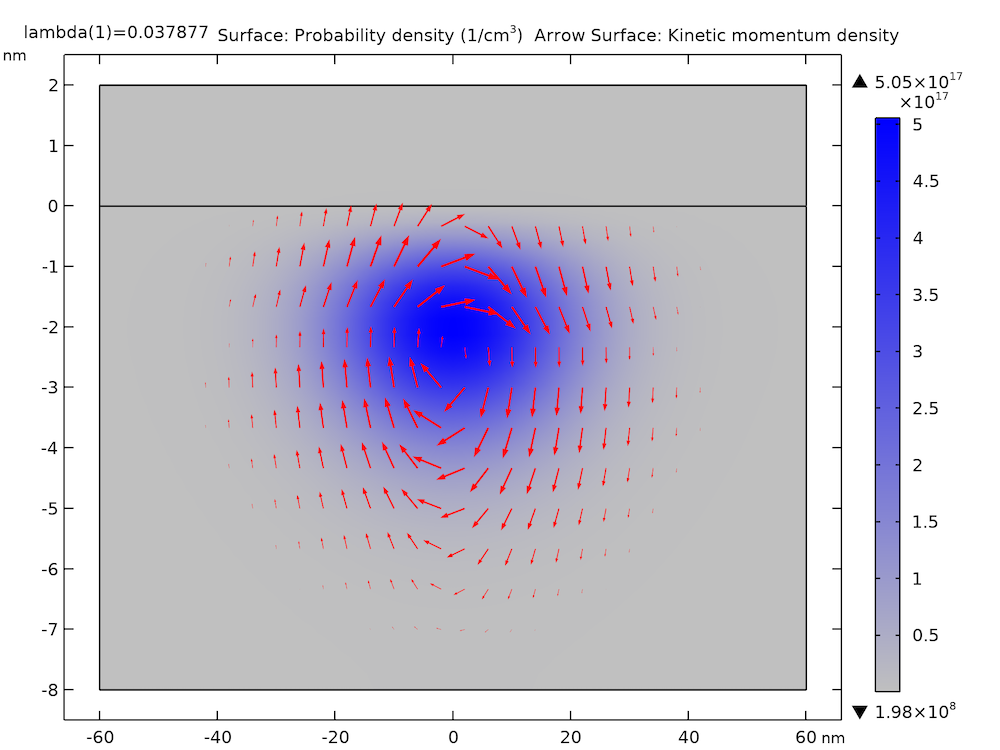
下のグラフは, xz平面上の基底状態の確率密度 (青灰色の勾配) と運動量密度 (赤い矢印) を示しています. これは論文の補足図 1 とよく一致しています.
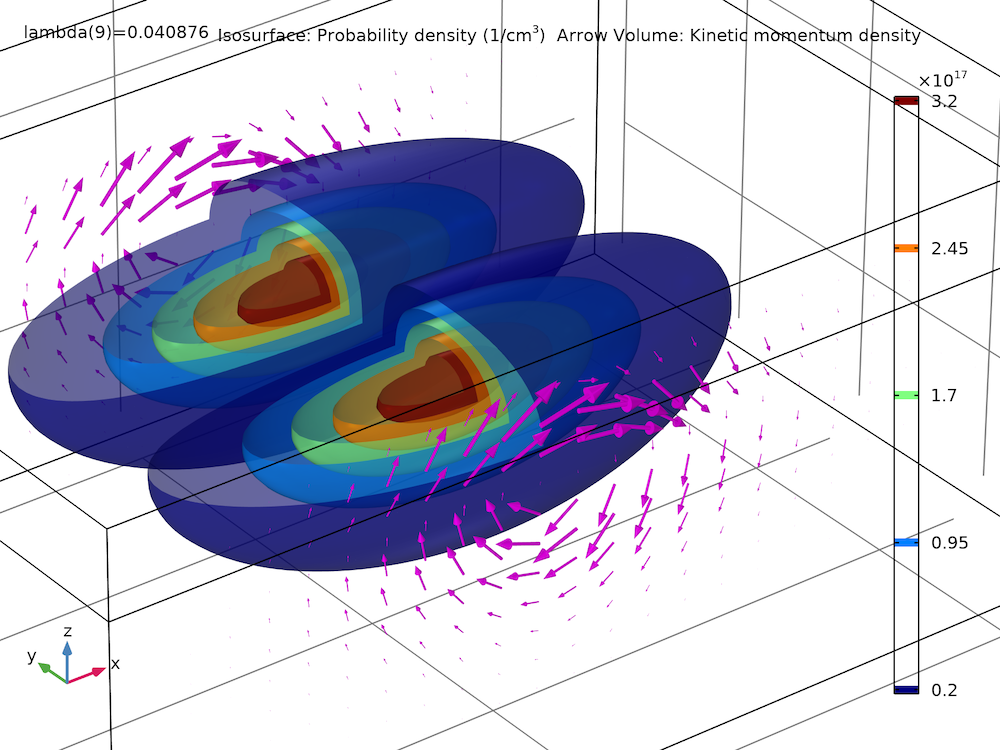
下のプロットは, モデルサムネイルの 8 番目の励起状態の確率密度 (等値面) と運動量密度 (矢印) を示しています. 確率密度の等値面は, COMSOL Multiphysics® バージョン 5.6 以降で利用可能な 透明度 サブノードを使用して部分的に透明になっています.
次はあなたの番です…
この投稿と前回の 歪みウルツ鉱 GaN バンド構造の k • p 法に関するブログ では, 多成分波動関数の シュレーディンガー方程式 フィジックスインターフェースの機能について説明しました. シミュレーション作業でこれらの機能をどのように使用しているか, ぜひお聞かせください.
下のボタンをクリックして, 均一な磁場内でシリコン量子ドットをモデル化してみてください. アプリケーションギャラリに移動し, MPH ファイルをダウンロードできます.
参考文献
- R.M. Jock et al., “A silicon metal-oxide-semiconductor electron spin-orbit qubit,” Nature Communications, 9:1768, 2018.



コメント (0)