小さな自動時間ステップに対抗するための戦略

以前のブログでは, BDF時間ステッピングスキームの時間ステップと離散化次数を選択するために使用されるメカニズムについて説明しました. これらのメカニズムは, 効率と堅牢性の間のトレードオフを伴う, 既定の許容誤差に従って解の精度を保証するように設計されています. このフォローアップでは, 小さな自動時間ステップが発生した場合にシミュレーション効率を向上させるためにどのような対策を講じるべきかを説明します. いくつかの例を見て, どのソルバー設定を調整できるかについて説明します.

ソルバーログでの時間ステップと離散化次数の追跡

BDF時間ステッピングスキームを使用して時間依存シミュレーションのソルバーログを検査する場合, BDFスキームの次数と時間ステップは, 前のブログで説明されているメカニズムによって異なります. 3つの潜在的なシナリオの1つに自分自身に当てはまるかもしれません:

シナリオ 1: 時間ステップと離散化次数の変更

ソルバーログから, NLfail = 0および Tfail = 0（時間依存ソルバーおよび代数ソルバーの失敗は記録されません）であることがわかりますが, 時間ステップと離散化次数の両方が変化しています.

これは典型的なシナリオであり, 正常に動作するモデルで予想される動作です. 局所切り捨て誤差が小さい場合, 時間ステップサイズは大きくなります. 離散化次数の増加は, 高次の時間微分が単調に減衰する滑らかな解を示します. 非線形性の影響は代数ソルバーによって処理され, いくつかの追加の代数ソルバーの反復またはいくつかの追加のヤコビアン更新によって反映されますが, これは時間ステップには影響を与えません.

いつもではありませんが, 通常, ソルバー設定の調整は必要ありません. ただし, 目前の問題に対して許容誤差が大きすぎて, 解の中のある効果や詳細が失われるリスクが常にあります. つまり解が十分に解像されていないことがあります. これは, すべての時間ステップで誤差推定値が満たされている場合でも発生する可能性があります. したがって, 許容誤差を減らしてシミュレーションを繰り返すことをお勧めします. これにより, 時間ステップが小さくなり, CPU時間が長くなる代わりに, 解の精度が向上します. また, 代数的終了基準は時間ソルバーの許容値に直接関連しているため, 許容値が大きすぎると, 時間離散化誤差だけでなく, 代数的問題の反復を終了することによるエラーにも影響を与えるリスクがあることに注意してください. .

したがって, 場合によっては, 許容値を下げると, 解の詳細の解像度が向上し, 誤差推定がスムーズになり, 時間ステップが大きくなる可能性があります. これらの場合に許容値を下げると, より効果的な（より速い）時間ステッピングにもつながるため, これはやや直感に反します.

例: 1次元粘性バーガーズ方程式

次のバーガーズ方程式を考えてみましょう.

ここで, 初期値は平滑化ステップ関数, 拡散係数c=0.001, 対流係数\alpha=1, 非線形対流係数\beta=1.

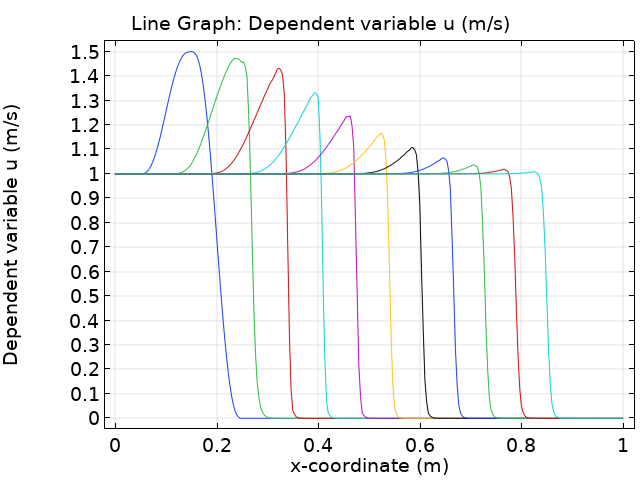
デフォルトのソルバー設定を使用して, 均一なディリクレ境界条件を持つ区間で2次ラグランジュ要素離散化(0,T] \times (0,1)を使用して解きます. 非線形性のため, 粘性衝撃プロファイルが形成されています. 妥当なメッシュサイズと許容誤差を特定するために, 最初にメッシュ収束解析を実行します.

参照解u_{\rm ref}は時間T=0.15まで計算され, 最大要素サイズh_{\rm max} = 1e-6( 自由度2e6に対応), 相対誤差 R=1e-5, 855 時間ステップ. 最大点誤差を次で定義e_{P1} := {\rm max}_{t \in (0,T]} |u(t,0.2)-u_{\rm ref}(t,0.2)|, e_{P2} := {\rm max}_{t \in (0,T]} |u(t,0.35)-u_{\rm ref}(t,0.35)|, 積分誤差を次で定義e_I := {\rm max}_{t \in (0,T]}\int_0^1 |u(t,x)-u_{\rm ref}(t,x)|dx. メッシュが粗すぎるか, 相対許容誤差が大きすぎる場合, 解に視覚的なスパイクがあります（下の表の赤い値を参照. スパイクは e_{P2}によってのみ反映されます）.

# は時間ステップ数を表します.

最初の列から, 相対許容誤差が大きすぎる場合, メッシュを細かくしても誤差を減らすことができないことがわかります. デフォルトの許容値を減らす必要があります. また, 許容誤差を小さくしても, メッシュが粗すぎる場合の誤差は減少しないことがわかります. 許容誤差が小さい場合でも, 特定のメッシュサイズで誤差が飽和します. 許容誤差が低くなると, 時間ステップの数が増加します（絶対許容誤差は相対許容誤差と関係していることに注意してください）. シミュレーションの過程で, 時間ステップは最初の数ステップでサイズが小さくなり, 最後までわずかに増加します. この例では, 許容される最大の許容誤差があります. 許容誤差が十分に小さい場合, 誤差の大きさはR= 0.0001メッシュの解像度に依存します. より細かいメッシュはより多くの時間ステップを与えないことに注意してください.

さらに, 許容係数を1から0.1に減らすことで, 実行される時間ステップの数を減らすことができることがわかります（表には示されていません）. その理由は, この設定では代数ソルバーの許容誤差が低くなり, 代数誤差による過渡誤差の汚染が少なくなるためです. ソルバーログから, シミュレーションが終了するまでBDFの次数は5のままであることがわかります（そうでない場合, 代数的誤差のために減少します）. 測定された誤差の合計は, 計算される時間ステップが少ない場合とほぼ同じレベルのままです. これは, 許容誤差を厳しくすると, より効率的な（より速い）時間ステッピングが得られることを示す良い例です. これは, 偏微分方程式を解くときに空間誤差と時間誤差の両方をどのように考慮する必要があるかを示す良い例でもあります.

この例では, TfailまたはNLfailに障害は記録されておらず, BDFの次数は1から5に急速に増加し, その後2から5の間で変化し続けます（許容係数が減少しない場合）. この簡単な例では, 代数ソルバーがうまく機能しています. このソルバーがはるかに高価なヤコビアン更新戦略（反復ごと）を使用している場合でも, 定数（ニュートン）から自動（ニュートン）に切り替えて同じ動作を取得することもできます. ただし, 自動高非線形（ニュートン）ソルバーの場合, NLfailが急速に増加し, 平均して1つおきのステップで失敗することがわかります. その理由は, このソルバーは控えめな減衰係数で始まり, 通常, 良性の問題であっても4回の反復で収束しないためです. これらの障害がどのように時間ステップを1e-3sではなく約1e-5sに短縮するかを確認することは説明になります. （100倍以上のステップが必要です！）これは, 時間ステッピングのパフォーマンスの劇的な低下です. 非線形ソルバーの失敗とより小さな時間ステップは, 完全連成ソルバーの最大反復回数を4から6に増やすことで修正できます（代数ソルバーがその仕事をする機会が与えられるように）.

非線形ソルバーで頻繁に失敗するのは, 減衰係数\omega=0.5と最大反復回数が2に制限された定数（ニュートン）の選択でも観察されます. 時間ステップが以前よりも小さくなることがわかります. 許容係数を10に増やすと, NLfailとTfailに障害が記録されます. 代数ソルバーを台無しにするのは奇妙に見えるかもしれませんが, それは時間依存の解法プロセスを台無しにする不適切に設定された代数ソルバーの例証として役立ちます. これらの誤差は, \beta=0が使用された場合にも持続します（線形問題）. 許容係数をさらに大きくすると, Tfailの誤差のみが発生します（代数ソルバーは大きな誤差を受け入れます）.

シナリオ2: ゼロより大きいNLfail

ソルバーログからNLfail > 0であることが分かります.

時間依存ソルバーは, 各時間ステップで, おそらく非線形の代数的問題の解を計算します. 代数ソルバーが失敗するたびに, NLfail列がインクリメントされます. 代数的反復のヤコビアン（またはヤコビアン）は, 計算に比較的コストがかかります. したがって, デフォルトでは, ヤコビアンの再評価は可能な限り実行されません（ヤコビアンの更新は最小限です）. 代数ソルバーが収束しない場合, 時間ステップが短縮され, ヤコビアン（またはヤコビアン）が再計算され, 代数問題が再度求解されます. これはかなり高価です. 時間ステップはヤコビ行列の一部であるため, 最小ヤコビ行列戦略でも線形問題の収束に失敗する可能性があることに注意してください.

時間ステップが大きくなりすぎて代数ソルバーが失敗し, それが何度も発生する場合は, 時間ステップ設定内で非線形コントローラーを有効にすることで状況を改善できます. これにより, 高度に非線形な問題では特に, より保守的な時間ステップ制御が可能になります.

それでも代数ソルバーが失敗する場合は, 最大反復回数を増やします. 次に, ヤコビアンの更新を 反復ごとにオンに変更します（または少なくとも 時間ステップごとに1回に変更します）. 次に, さまざまな加速またはロバスト化の方法を試すことができます. アンダーソン加速は, 分離代数ソルバーと一緒に使用すると便利です. 代わりに, 完全連成ソルバーに切り替えると役立つ場合があります（使用可能なメモリの量が許す場合）. 完全連成ソルバーの場合, 一定の減衰係数を下げるか, 自動減衰法を使用すると便利です.

それでも代数ソルバーが収束しない場合は, ソルバーログを詳細に変更して, 個々の従属変数の誤差推定値を取得できます（COMSOL Multiphysics®バージョン5.5以降）. この情報は, ログビューに出力されるだけでなく, 別の収束プロットウィンドウにも表示されます. この情報を使用して, どの変数が代数的誤差を支配しているかを追跡できます. これにより, 収束の問題についての洞察が得られます. 従属変数の誤差の重みは, その変数のスケーリングと絶対許容誤差の選択の両方の影響を受けることに注意してください.

代数ソルバーの終了に直接影響するもう1つの重要なパラメーターは, 許容係数です. 値1は, 代数的問題の終了基準が局所時間ステップ誤差の場合とほとんど同じであることを意味します. 一部のフィジックスインターフェースは, この係数をより小さな数に変更します. この係数を増やすと, 収束基準を簡単に満たすことができますが, 同時に, 代数的誤差が解を汚染するリスクがあります. この要素を選択するときは, 注意が必要です.

代数ソルバーの失敗は, 線形ソルバーの失敗によっても発生する可能性があります. 線形ソルバーには, 代数ソルバーが終了するのを防ぐ自動エラーチェックメカニズムがあります. これは, ログウィンドウのLinErrまたは LinRes, あるいはその両方の列の数値が小さくない場合に問題になる可能性があります. これが実際に当てはまることを確認するために, 線形ソルバーの誤差推定値のチェックをはいに設定できます（エラーセクションの下）. これにより, 要求された精度で求解できない線形行列の問題が発生するとすぐに, 時間ステッピングが停止し, エラーが発生します.

直接線形ソルバーの場合, 反復改良（直接線形ソルバーのエラーセクションを参照）とオプション非線形ソルバーで使用を有効にすることで, 状況の改善を試みることができます. 反復線形ソルバーの場合, 誤差推定の係数を増やすことで終了基準を緩めることができますが, そうしないと, 解を汚染する代数的誤差が増える可能性があるため, これは注意して行う必要があります.

反復線形ソルバーの場合は, LinErrと LinResの数値に注意してください. これらの数値が十分に小さくない場合, 問題は, 前処理行列が, 解かれる行列に対して十分な品質ではない可能性があります. 前処理行列を微調整する代わりに, 線形反復ソルバー設定が実際に解かれる行列を対象としているかどうかを最初に確認できます（デフォルトソルバーを表示を使用）.

例: マルチターンコイルの磁場

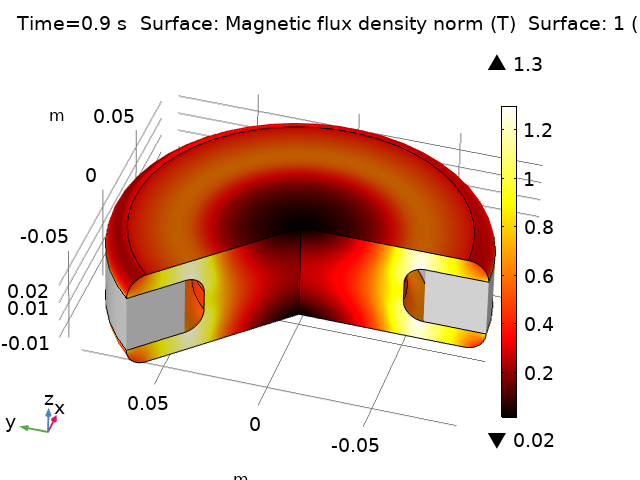
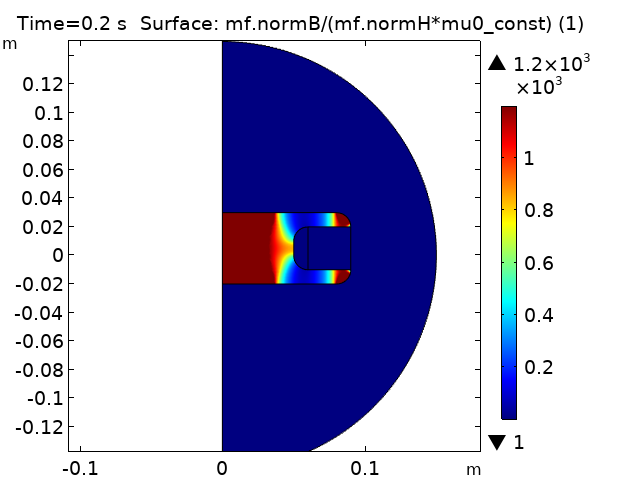
2次要素を備えた磁場インターフェースを使用して, 正弦波電流によって励起された銅マルチターンコイルの時間依存磁場を調べてみましょう. 銅コイルは空気に囲まれ, 非線形の構成関係（非線形のB-H曲線）を持つ軟鉄片で吊り下げられています.

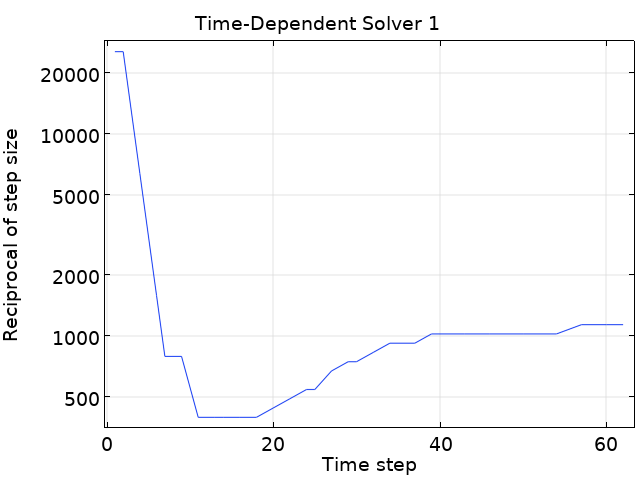
時間依存ソルバーの時間リストをrange(0,0.1,10)に設定し, デフォルトのソルバー設定（完全連成, 定数（ニュートン）, 直接, および最小ヤコビアン更新）と10 Aの正弦波コイル励起を使用して, 5つの時間区間（終了時間10秒）にまたがる解は, 約100の時間ステップで達成されることがわかります. この種のフィジックスのデフォルトの時間ステッピングスキームは, ソルバーが実行するステップの中間設定を使用していることに注意することが重要です. 結果として, 指定された出力時間は, 時間ステップに0.1秒の上限を設定します. これは, ソルバーログを調べることで確認できます. 励起が30Aに増加する場合, 出力時間による上限時間ステップ制約を下げる必要があります（たとえば, 合計で約200時間ステップで0.05秒に）. それ以外の場合, 収束した解はありません.

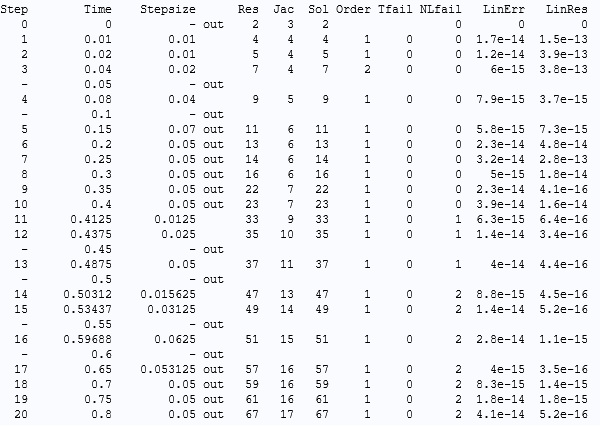
40 Aのコイル励起の時間ステッピング動作をより詳細に調べてみましょう. 出力時間によって最大ステップ制約を下げる戦略は生産的ではないようです（ステップ制約0.001秒でも機能していません）. range(0,0.05,10)に等しい時間の場合, NLfailの失敗がいくつか見つかり, ソルバーは実際には109時間ステップ後にエラーメッセージを出して求解をあきらめます:

…

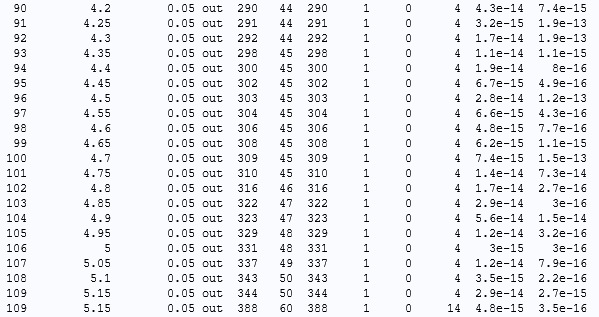
マルチターンコイルモデルの磁場の出力間隔0.05秒の励起40Aおよびデフォルト設定のソルバーログ.

失敗の理由は最後の行にあります：10回繰り返されるNLfail. 10回失敗すると, ソルバーは次のステップに進む前に諦めます. この時点で, 時間ステップは1/4の10分の1に短縮されています. これは, 1,000,000分の1の時間ステップに相当します. ここでは, ステップサイズは問題ではない可能性があります. 試行ごとに, 非線形ソルバーは最大反復回数内に収束しません.

コイル電流の5つの全周期である10秒をシミュレートしています. コイル電流がゼロの場合, ベクトルポテンシャルはゼロなので, スケールについて少し考える必要があります. ログを調べると, 磁場のポテンシャルに1の自動スケールが与えられていることがわかります. ソルバーが停止したときのベクトルポテンシャルをプロットすることにより, 電流のゼロ交差ではなく, 磁気ベクトルポテンシャルのスケールを約1e-2 Wb/mと見積もることができます. 自動スケーリングのデフォルトは, 解のノルムに基づいて絶対許容誤差を更新することであるため, ベクトルポテンシャルの手動スケーリングに変更することをお勧めします.

ソルバー設定変更戦略

上記のシナリオ2で提案された手順に従いましょう.

1. 磁気ベクトルポテンシャルの手動スケーリングを1e-2に変更します. 再試行しても, 改善はありません.
2. 完全連成ソルバーの最大反復回数を10に変更します. 再試行しても改善はありません. これはかなり非線形の問題のようです.
3. ヤコビアン更新戦略を時間ステップごとに1回に変更します. もう一度試してみると, NLfailの障害は報告されずに約200の時間ステップで解決策が達成されていることがわかります（ただし, 時間ステップの制約を緩和することはできません）.
4. ヤコビアン更新戦略を反復ごとに変更します. もう一度試してみると, これが本当に違いを生むことがわかります！これで, 28時間ステップの自由時間ステップでも求解できます（わずかに大きな誤差がありますが, 誤差推定は規定の許容範囲を満たしています）.
5. 次に, 中間時間ステップと最大ステップ0.05秒の結果が正確な結果であるかどうかを自問する必要があります. ベクトルポテンシャルは, 約1e-16 Wb/mであるゼロ交差（t = 0.5 sの倍数）を除いて, 約1e-2 Wb/mと計算されます. スケーリングは正しいようです. 参照用に解のコピーを作成し, より厳しい許容誤差で新しい計算を行います.
6. スタディの相対許容値を0.0001に変更して, 収束チェックを行います. これは絶対公差の引き締めにも対応していることに注意してください. 100分の1の許容誤差の問題を求解することにより, モデルのロバスト性テストを行います. 再び約200時間ステップかかり, 代数的反復が約5％多くなります. NLfailと Tfailの障害はありません. この計算結果とコピーの名目上の差は1e-5Wb/mのオーダーであるため, 時間離散化には小さな誤差があると結論付けることができます. このブログでは, 空間誤差は考慮されていません.
7. 100 Aの励起の場合, ソルバー設定が調整され, 最大時間ステップが0.05秒の解でも, 中間時間ステップとデフォルトの許容誤差で1％未満の誤差の結果が得られます.

この実験では, デフォルトのソルバー設定が10 A励起に対して完全に適切であることがわかりました. 励起をオンにすると, 非線形効果がはるかに強くなります. ソルバーにとって, これは低コストと堅牢性の間のトレードオフです. より非線形な領域では, ロバスト性を手動で上げる必要があります. 一方, より堅牢な設定では, 励起が低い場合にパフォーマンスが低下します.

シナリオ3: ゼロより大きいTfail

ソルバーログからTfail > 0が分かります.

時間依存ソルバーがとる時間ステップの失敗は, 許容誤差に関して制限された誤差が満たされないことを意味し, 時間ステップはより小さなステップサイズで繰り返す必要があります. 新しいステップサイズは, 前に概説したメカニズムによって決定されます. 失敗するたびに, Tfail列がインクリメントされます. これは, 局所エラーの変化を正しく予測しないため, 時間ステップコントローラーの障害と見なす必要があります.

時間ステップの短縮とステップの再計算は緊急操作です. これが（非常に一時的な性質のために）予測が容易ではなかった解の一時的なものが原因で発生した場合, これを改善するのは難しい可能性があります（実行する手順をさらに制御する必要があります）. 一方, これが定期的に発生し, 解の遷移がない場合は, 改善の余地があります.

一般的な原因の1つは, 誤差推定がスムーズでないため, ステップごとに大きく異なることです. これは, （BDFソルバーで）使用される低次数によって明らかになります. 場合によっては, 相対許容誤差を減らすか, 代数的許容係数を減らして代数的誤差を抑制することが解決策になります. 偏微分方程式の問題を解く場合, 空間メッシュが粗すぎることが原因である可能性もあります. 解決策は, メッシュを改良するか, より空間的な安定化を導入することです. このシナリオの最後の手段は, 代わりに手動タイムステッピングを使用することです（Tfailは不可能ですが, エラー制御もありません）. その他のオプションには, より小さな初期ステップの使用, または時間ステップセクションでの最大ステップ制約の適用が含まれます.

NLfailと Tfailの両方も増加する可能性があります. 代数ソルバーの誤差は, 時間ステップ選択メカニズムの失敗に関連している可能性があります. このようなシナリオでは, 代数ソルバーと時間ステッピングメカニズムの両方を調整する必要があります. ただし, この戦略は, 問題が適切に設定されている場合にのみ成功します. それ以外の場合は, すべての賭けが無効になります.

例: 流体ダンパー

流体ダンパーの例では, 衝撃を遮断したり, 地震による揺れや風による振動を抑制したりするためのデバイスをモデル化しています. このモデルは, デバイス内の粘性加熱の現象をシミュレートします.

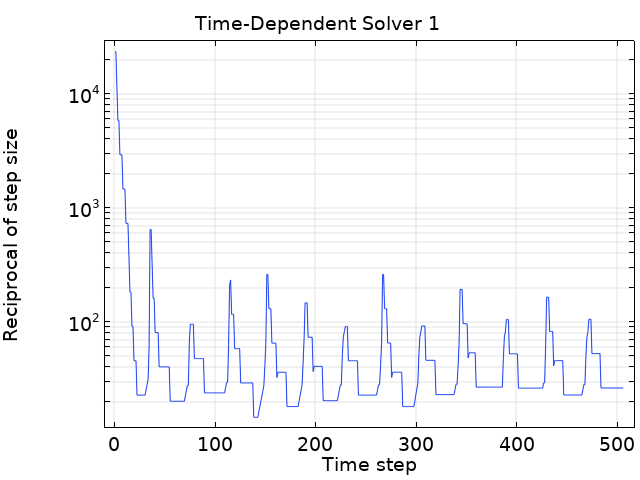
このモデルは, シミュレーションの過程で時間ステップがどのように変化するかを示す良い例です. デフォルトのソルバー設定では, Tfailについていくつかの失敗が記録されます.

これらの障害を防ぐ方法と, シミュレーションのパフォーマンスを向上させる方法を見てみましょう. 周期的な負荷により, 流体は交互に上下に移動します. これは, 速度と圧力勾配の場が方向を変え, ゼロ交差を通過することを意味します（短時間のすべてのDOF）. この場合, 絶対公差はターニングポイントの近くで非常に小さい値になるため, 絶対公差の自動更新は複雑になる可能性があります. ログを調べて定期的なピストン変位と比較すると, これらのポイントの近くでTfailが発生していることがわかります. 一方, スケールは大きく異なります.

最初のアイデアは, 絶対許容値セクションの時間依存ソルバーのスケーリングされた絶対許容値を更新するチェックボックスをオフにすることです. これは動作しません. 代数変数設定セクションでは, 誤差推定が代数を除外するように設定され, 圧力の許容係数（comp1.pが0.05に設定されていることに注意してください.

従属変数ノードの下の変数ノードで手動スケールを使用してみましょう. スケーリングセクションの方法を手動に設定し, 圧力にスケール1e7, 温度に1e2, 速度場に1e1を使用します. さらに, 圧力と温度には0.1の許容係数を使用し, 速度には0.5を使用します. Tfailはもうありませんが, 代わりに6つのNLfailがあります. 主な利点は, 1300ではなく約400の時間ステップのみが使用されることです. たとえば, 分離ノードの最大反復回数を15に設定し, アンダーソン加速の反復空間の次元を8に設定することで, NLfailを減らすことができます. これらの変更により, 計算時間が大幅に節約されます.

例: 増幅回路のインダクター

増幅回路のインダクターの例は, 電気回路シミュレーションと有限要素シミュレーションを組み合わせる方法を示しています. このブログのコンテキストでは, これは, 時間ステッピングスキームの動作を最適化するために許容係数を調整する例です. この場合, 作業を節約するには, ヤコビアン更新の最小設定を使用した追加の代数的ステップで十分です. モデルに保存されているソルバー設定を使用すると, 定常で時間依存のスタディ2の解は, 170ステップ, 10 TFail, 1 NLfail以内であることがわかります.

許容係数を0.1に下げ, 最大反復回数を6に増やすと, ヤコビアン更新の設定に触れることなく, ステップ数が2TFailと0Nfailで127に減少することがわかります. 残りの Tfailは, 最初のステップから発生します. これらは, たとえば, 最初のステップを1e-9sに下げることによっても回避できます. ただし, これによるメリットはわずかです. この例では, 許容誤差が厳しくなると, 求解プロセスが大幅に効率化されます.

自動時間ステップと次数選択についてのまとめ

このブログでは, ソルバー設定のコツと, 時間依存のソルバーログから何を読み取るかについての戦略を示しました. これらのトピックの詳細については, COMSOLのナレッジベースを参照してください.

関連資料

COMSOLナレッジベースのこれらの記事で詳細をご覧ください:

• 非線形時間依存モデルの収束改善
• 過渡モデルの収束改善
• 時間依存ソルバー時間ステップの制御