波動光学計算のための非近軸ガウシアンビーム公式

以前のブログでは, 近軸ガウシアンビーム公式について説明しました. 今日は, COMSOL® ソフトウェアのバージョン5.3 a で利用可能な, ガウシアンビームのより正確な定式化について説明します. 平面波展開に基づくこの定式化は, 従来の近軸定式化よりも非近軸ガウシアンビームをより正確に処理できます.

ガウシアンビームの近軸性

よく知られているガウシアンビームの公式は, 近軸ガウシアンビームにのみ有効です. 近軸とは, ビームが主に光軸に沿って伝搬することを意味します. 量的な意味での近軸性について論じている論文がいくつかあります (参考文献1を参照).

大まかに言えば, ビームのウエストサイズが波長に近い場合, ビームは焦点に対してより大きな角度で伝播します. したがって, 近軸性の仮定は成り立たず, 定式化はもはや正確ではありません. この問題を軽減し, 一般的なガウシアンビームのより一般的で正確な定式化を提供するために, 非近軸ガウシアンビーム定式化を導入しました. ユーザーインターフェースでは, これは平面波展開と呼ばれます.

この方法は平面波の角スペクトルに基づいており (参照2), 角スペクトル法と呼ばれることもあります (参照3).

平面波の角スペクトル

2D での近軸ガウシアンビーム式を簡単に確認しましょう (視覚と理解を深めるため).

時間調和場を仮定したマクスウェル方程式から始めます. そこから, 波長 \lambda における面外偏光の電場に関する次のヘルムホルツ方程式が得られます.

ここでk=2 \pi/\lambda.

平面波の角スペクトルは, 次の単純な事実に基づいています. 上記のヘルムホルツ方程式を満たす任意の場は, 次の平面波展開で表すことができます.

ここで, A(k_y)は任意の関数です.

積分経路は, 実数の k_x と k_y の半径 k の円です. (複素数 k_x および k_y の場合, 積分領域は複素平面に拡張されます.) 関数 A(k_y) は角スペクトル関数と呼ばれます. この E_z は, 直接代入によってヘルムホルツ方程式を満たしていることを証明できます.

この定式化が常にヘルムホルツ方程式の正確な解を与えることがわかったので, 視覚的に理解してみましょう. k_x^2+k_y^2=k^2 という条件から, k_x=k cos(\varphi) と k_y=k sin(\varphi) とし, 上記の方程式を次のように書き直すことができます.

上記の式の意味は, 波数 k がすべて同じで, さまざまな方向に伝播する多くの波で構成される和または積分として波を構成するということです. これを次の図に示します.

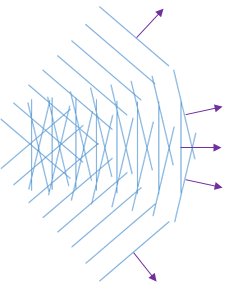
平面波の角スペクトルの可視化.

k_y で書き直されたの公式に戻って, この式を使用して実際に問題を解くには, 境界条件を満たす角スペクトル関数 A(k_y) を見つければよいだけです. 横方向の場のプロファイル（伝搬方向, つまり光軸に垂直）もガウシアン形状であると仮定すると (参照4を参照), A(k_y) = \exp(-k_y^2 / w_0^2) を導出できます. ここで, w_0 はスペクトル幅です.

さらに数学的操作により, スペクトル幅 w_0 とビームウエスト半径の関係が得られます. たとえば, 平面波は, 角スペクトル関数がデルタ関数である極端な場合です. 低角ガウシアンビームの場合, 角スペクトルは狭くなります. 広角ガウシアンビームの場合, 角スペクトルは広くなります.

これは, 非近軸ガウシアンビームの基礎となる理論の簡単な要約でした. これまでに示したことを要約するために, 極座 x=r \cos \theta, \ y = r \sin \theta: を使用して式をもう一度書き直してみましょう.

これは, Born と Wolf (参照2) が使用している定式化です.

3D の公式はより複雑で, 異なる偏光表現のために色々な定式化がありますが, 基本的な考え方は上記の参考文献に見られるものと同じです. また, エバネッセント波を考慮するかどうかによっても異なる式になる場合があります. 波動光学モジュールと RF モジュールで使用される平面波展開法は, 角スペクトル理論に基づいていますが, 数値計算として適用されています.

平面波展開: 設定と結果

新しい機能である平面波展開を, 以前に利用可能だった機能である近軸近似と比較してみましょう. 両方の方法をカバーする設定ウィンドウを以下に示します.

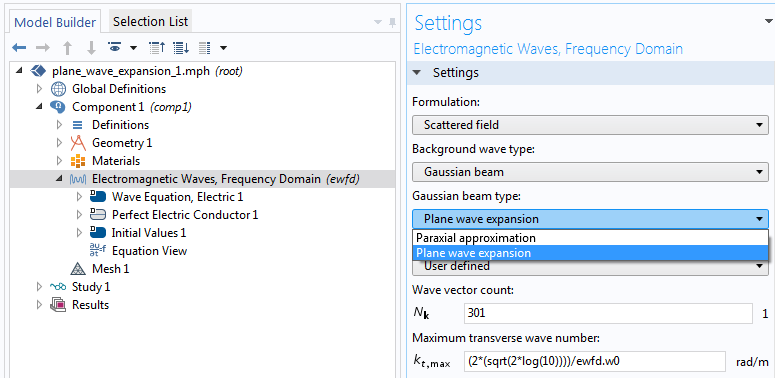
平面波展開機能の設定

新機能では, 自動設定で十分な概算が得られない場合, 2つのオプションがあります.

1. 波数ベクトルカウント
2. 最大横波数

最初のオプションは, ガウシアンビームをどの程度細かく表現するかに応じて, 離散化レベルの数を決定します. 平面波が多いほど, 細かくなります. 2番目のオプションは, 前の式の積分限界に関連しています. つまり, -\pi/2 \le \varphi \le \pi/2 この積分境界は, 可能な最小のスポットサイズの場合は最大 \pi/2 になり, ガウシアンビームの収束/発散角度に応じて, 低角のビームの場合はより小さくなります. より広角な (タイトフォーカスの) ビームを表すには, より大きな横波数を持つ, より角度のある平面波が必要です.

次の結果は, スポット半径が \lambda/2 であり, かなり非近軸である場合の2つの式を比較しています. 前のブログと同様に, シミュレーションは散乱場定式化で行われ, ドメインは完全一致層 (PML) に囲まれています. このように, 散乱場は正確なヘルムホルツ解からの誤差を表します.

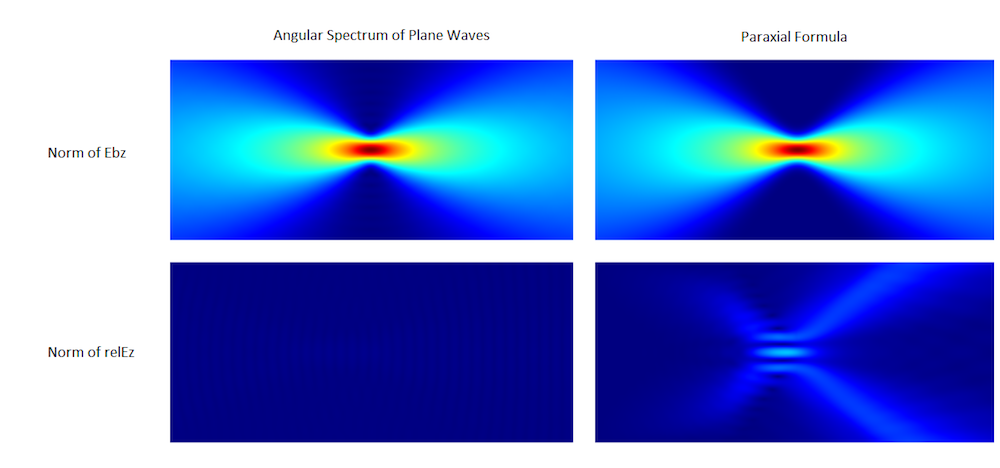
下の左の画像は新機能を示し, 右の画像は近軸近似を示しています. 上の画像は, 計算されたガウシアンビームの背景場 ewfd.Ebz のノルムを示し, 下の画像は, 正確なヘルムホルツ解からの誤差を表す散乱場 ewfd.relEz を示しています. 明らかに, ヘルムホルツ解からの誤差は, 非近軸法で大幅に減少します.

平面波角スペクトル法と近軸式の比較.

まとめ

新しい平面波展開オプションを使用した非近軸ガウシアンビームの近似法の理論と結果について説明しました. この定式化は非常に正確ですが, それでも仮定の下での近似値であることを忘れないでください. まず, 焦点面の場の形状を仮定しました. 次に, エバネッセント場がゼロであると仮定します. 高角ガウシアンビームの焦点領域近くのナノ構造への場の結合に関心がある場合は, エバネッセント場を計算する必要があります. 非近軸ガウシアンビームのエバネセント成分について詳しくは, 以前のブログ: 非近軸ガウシアンビームのエバネセント成分をご覧ください.

次のステップ

下のボタンをクリックして, COMSOL® ソフトウェアで光学的に大きな問題をモデル化するために利用できる定式化と機能の詳細をご覧ください.

注: この機能は, RF モジュールにも搭載されています.

参考文献

1. P. Vaveliuk, “Limits of the paraxial approximation in laser beams”, Optics Letters, vol. 32, no. 8, 2007.
2. M. Born and E. Wolf, Principles of Optics, ed. 7, Cambridge University Press, 1999.
3. J. W. Goodman, Fourier Optics.
4. G. P. Agrawal and M. Lax, “Free-space wave propagation beyond the paraxial approximation”, Phys. Rev. a. 27, pp. 1693–1695, 1983.