特定のモデリング問題は, 特に優れたソリューションにつながることがあります. 最近, そのようなケースの1つとして, 非線形電気回路に関する問題に対する時間周期定常解を見つけるというケースが挙げられます. このケースを詳しく見て, ソフトウェアのコア機能のいくつかが効率的な実装にどのように役立つかを見てみましょう.
モデリングのシナリオ: 非線形トランスフォーマー
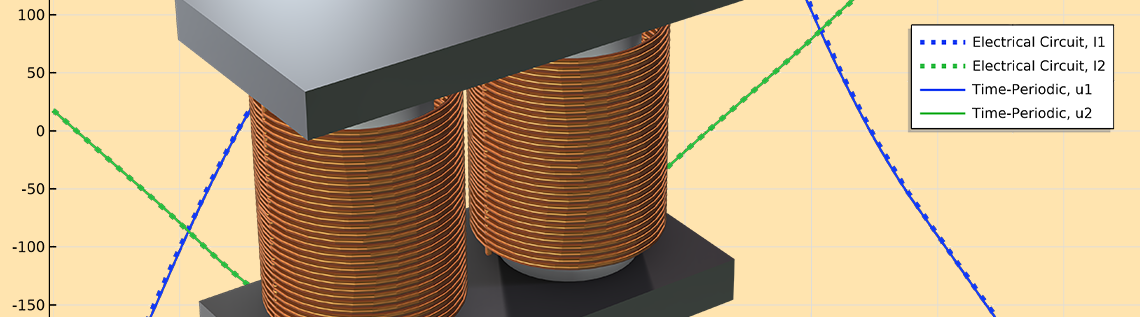
以前のブログ差動インダクタンスとコイル機能の使用で, 非線形コア材料の周りに巻かれた2つのコイルで構成される変圧器のケースについて検討しました. 正弦波の AC 電圧を印加すると, 一次コイルと二次コイルに電流が流れますが, 電流が十分に高い場合, 材料の非線形性によって差動インダクタンスが大幅に変化し, 誘導電流は非正弦波になります. この動作は, デバイスの完全忠実度モデルを作成するか, 非線形差動インダクタンスを考慮した等価電気回路モデルを作成することでモデル化できます. 非線形性により, 時間的には非正弦波ではあるものの, 周期的な電流が発生します. この緩やかな応答は, 過渡モデルを多くの期間実行することで観察できます.
非線形コアの周りに巻かれた2つのコイルで構成される変圧器. 差動インダクタンスは有限要素モデルから抽出され, 等価回路モデル内で使用できます.
等価回路モデルを多数の周期にわたって実行した結果, 時間周期的な定常状態に徐々に近づいていることがわかります.
結果を見ると, 多くの期間にわたってシミュレーションする必要があることは明らかであり, 時間周期的な定常解のみに関心がある場合は, 生成されたデータの大部分は実際には必要ありません. 理想的には, この状況では, 時間周期的な解に直接つながる方法が必要であり, それがここで取り上げるものです.
等価回路を時間から空間へと再定式化
電気回路モデルを詳しく見てみると, 時間とともに変化する未知数は2つだけであることがわかります. I_1 と I_2 は, 一次側と二次側を流れる電流です. 回路図を見ることから, 2つの電流ループの各要素の電位降下という観点から見てみましょう.
ここで, 差動インダクタンスはすべて両方の電流の関数です: \partial L_{ij} (I_1,I_2) . この一連の連立常微分方程式は, 色々な方法で解くことができます. ここでは, 印加電圧 V_{AC} と, 解が1周期 T_0 にわたって時間周期的である場合に限定します.
これは, 電流の時間微分を除いて, ほぼ非線形代数方程式であることがすぐにわかります. しかし, これを空間微分に置き換えたらどうなるでしょうか? それが私たちをどこに導くかを見てみましょう!
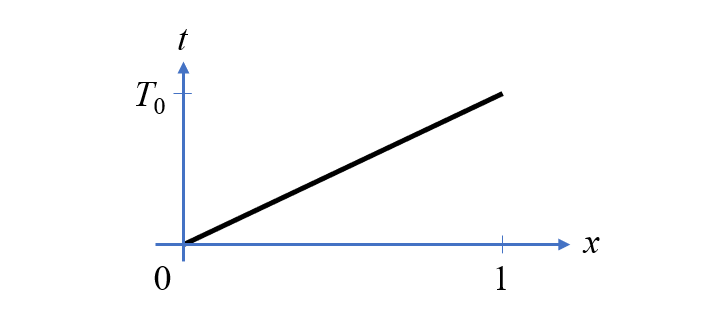
1D単位領域に沿った位置の関数としての時間.
1D領域 (単位長さの直線) を考えてみましょう. ここでは長さに沿って線形に変化する準時間変数を定義します. この直線に沿って2つの空間的に変化する変数 u_1 と u_2 を定義し, この直線に沿ってメッシュを導入すると, COMSOL Multiphysics® ソフトウェアは微分演算子 d (u1,x) を介して空間微分 \partial u_1 / \partial x を取得できます. ただし, 空間次元を時間次元として考えているため, これは実際には時間微分です. これを念頭に置いて, 単位長さの直線上で定義された Domain ODEs and DAEs インターフェースを使用して, 場の代数方程式を構築できるようになりました. インターフェースは以下に示されており, 2つの未知数が定義されています. これらの場にはラグランジュ要素を使用します. これにより, 連続場が自動的に保証され, 場とソースの単位を適切に設定できます. 読みやすさのために, 以下のスクリーンショットに示すように, 回路モデルの各部品による電圧降下を表す一連の変数を定義することもできます.
ドメイン常微分方程式と微分代数方程式のインターフェースを設定すると, 場の変数に名前が付けられ, 形状関数が選択され, 単位が設定されます.
時間空間領域での印加電圧, 電流の微分, および回路のさまざまな部品間の電圧降下を定義する変数.
これらの変数は, ドメイン ODE および DAE インターフェースの代数方程式機能内で使用されます. この機能には, 常にゼロに等しくなければならない方程式用の場が2つあります. ここでは, 2つの電流ループの電位降下の合計とソースを入力します. これらは, 前に示した方程式です. 最後に, 2つのポイント拘束がドメインの一方の端のポイントに追加されます. ここでの拘束は, もう一方のポイントで定義された積分機能に基づいています. u1-intop1 (u1) と u2-intop1 (u2) の拘束は, 周期性条件を強制します.
単位領域に沿った時間空間のどこでも満たされる方程式を設定.
ポイント拘束と積分機能を介して周期条件を定義.
この定常問題を解くには, デバイスが非線形領域に駆動されるときに, ドメインに沿って比較的細かいメッシュが必要です. したがって, 単位線に沿ったメッシュサイズは, この非線形定常モデルを解くときに検討する必要がある1つのパラメーターです. 結果は以下にプロットされ, 過渡結果と比較されていますが, 優れた一致を示しています. 実際, 過渡モデルをさらに厳しい許容値で解くと, 小さな相違は減少します. これにより, このような小さなモデルでも計算コストが実時間で1分程度増加しますが, 定常問題はほぼ瞬時に求解されます.
電気回路モデルから計算された過渡結果と時間周期アプローチからの定常結果の比較.
空間内の1周期にわたる解により, 空間 FFT データセットを介して周波数成分を抽出することもできます. この機能の設定は, 下のスクリーンショットに示されており, 配列1Dデータセットが強調表示されています. これは, 時間空間解ｓを定期的にパターン化して, 結果がより滑らかに見えるようにします. 適切に正規化された量をプロットすることで, 印加電圧が増加すると周波成分がどのように増加するかを確認できます.
空間 FFT データセットは, 時間方向に沿って定常結果を繰り返す配列1Dデータセットを入力として受け取ります.
AC 電圧が増加するにつれて周波数内容が変化するグラフ.
おわりに
このブログでは, 一連の代数方程式で記述できる系の時間周期的定常状態を解く場合に特に魅力的なアプローチについて説明しました. このアプローチでは, 滑らかで時間周期的な解が存在する限り, 正弦波強制関数だけでなく, あらゆるタイプの適用信号が許容されることに注意してください. 設定は非常にシンプルで, COMSOL Multiphysics® のコア機能を活用しているため, このアプローチは電気回路だけでなく, あらゆるタイプの問題に役立ちます. これは, COMSOL ユーザーが持っていると便利なテクニックです.
これに関連するサンプルモデルはここからダウンロードできます:
コメント (0)