
COMSOL Multiphysics® ソフトウェアでは, 隣接する領域に異なる不連続メッシュを使用できることをご存知でしたか? ソフトウェアの通常のデフォルト動作では, 整列したメッシュを使用しますが, 共役熱伝達をモデル化する場合など, 不連続メッシュを使用する方がよい場合もあります. このトピックをさらに詳しく調べ, これらのメッシュが, ほんの少しの労力で初期モデル開発の時間とメモリを節約できる方法を見てみましょう.
場の連続性を維持し, 整列した要素間の流束のバランスをとる
有限要素法 (FEM) の基本理論については, これまで何度も取り上げてきました (この 弱形式に関するブログなど). そのため, ここですべてを網羅することはしません. 代わりに, 重要なポイントを 1 つ確認します. 異なる有限要素間のインターフェースでは何が起きるのでしょうか. 簡単に言うと, 標準 FEM を使用すると, 隣接する整列した要素は同じノード ポイントを共有します (ノード ポイントは, 問題の解が計算されるポイントです). これらの要素はノードを共有するため, 解く場 (温度, 固体変位, 流体速度など) は自動的に連続します.
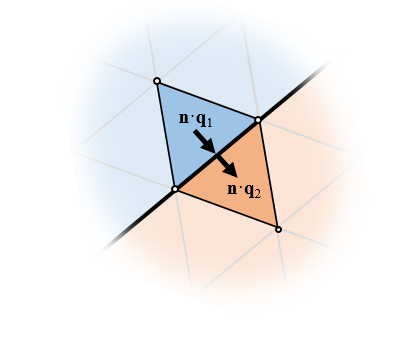
異なるドメインの要素間で流束が自動的にバランスされ, これらの要素は同じノードを共有するため, 場は連続的になります.
さらに, 流束は自然に等しくなるように強制されます (ただし, これには FEM の導出に関するもう少し徹底した理解が必要です). ここで, 流束という用語は, 扱う物理法則に応じて, さまざまな量を指すことがあります. 簡潔にするために, 熱伝達についてのみ考えます. ここでは, 自然に熱流束(熱伝導率と温度場の勾配の負数を掛けたもの, つまり \mathbf{q} = -k \nabla T) と呼びます. 要素間の境界では, FEM は自動的に (つまり, ユーザー入力や追加の内部方程式を必要とせずに) \mathbf{n \cdot q_1 =n \cdot q_2 } という条件を強制します. ここで, \mathbf{n} は要素間の境界に対する法線ベクトルです. つまり, 標準 FEM は, 場の連続性を自然に強化し, 流束のバランスをとります. これに関係なく, モデルの全体的な精度に自信を持つためには, 常に メッシュ細分化スタディ を実行する必要があることに注意してください.
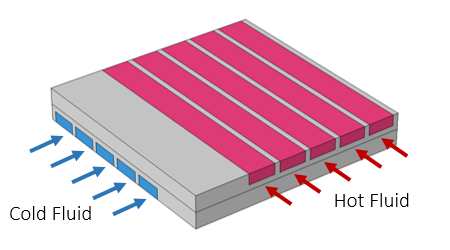
交差流れ熱交換器のサブモデルの概略図.
ここで, アプリケーションギャラリのサンプル モデルである 交差流れ熱交換器 を見てみましょう. このモデルは, 上に図解されています. これは, 直線の長方形流路で構成される, より大きな熱交換器のサブモデルです. 流路を通る流体の流れがモデル化され, 流体と周囲の固体の温度場もモデル化されます. 温度場は下にプロットされています. 温度は, 流れ流路の長さに沿った代表的な線に沿ってもプロットされています. これらのプロットから, 流れ流路に沿った温度変化は, 長さに沿っては非常にゆっくりと変化し, 流れ流路の断面では急速に変化し, 金属部分では非常に複雑な方法で変化していることがわかります.
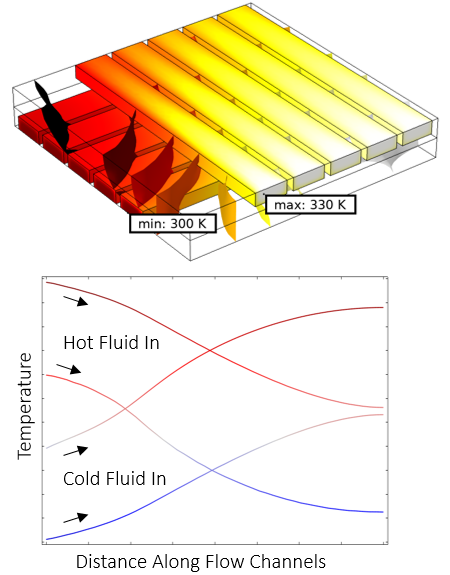
壁面の温度場と固体内の温度等値面 (上), および流路方向に沿った温度のプロット (下).
メッシュは以下にプロットされており, 流体領域と固体領域の間で連続していることがわかります. メッシュは主に四面体要素で構成されており, 流路壁の流体側に境界層メッシュが適用され, 壁近くの高速度と温度勾配を求解します.
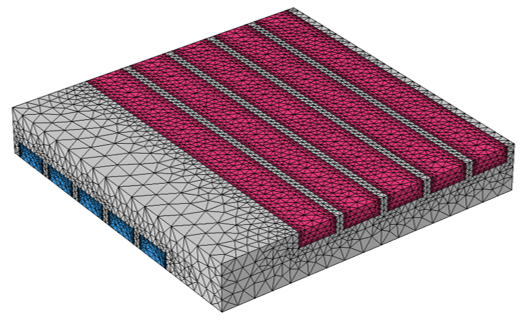
流体と固体の間で連続する交差流れ熱交換器のデフォルトメッシュ.
現在, このデフォルトのメッシュは, ユーザーの操作なしで生成されています. しかし, メッシュを手動で構築したい場合, またメッシュを不連続にしたい場合はどうなるでしょうか. その場合は何ができるでしょうか. それを実装する方法を説明する前に, ソフトウェアで何を行う必要があるかを見てみましょう.
磁場の連続性を維持し, 非整列要素間の流束のバランスをとる
下の画像に示すように, 2 つの隣接するドメインに要素の集合があるとします. 要素には隣接する境界がありますが, ノードは整列していません. この種類のメッシュは, アセンブリ ジオメトリの最終処理 ステップを使用すると自動的に生成されます. 個別のオブジェクトのメッシュは接続されないため, 結果として, この境界を越える場は不連続になり, ドメイン間の流束は発生しません.
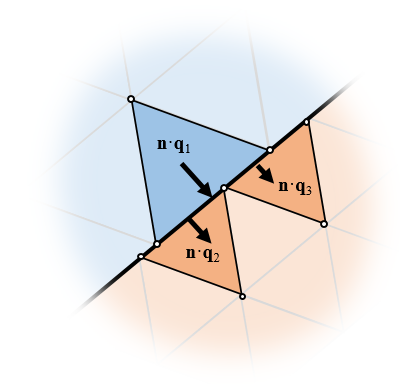
非整列メッシュの場合, 流束と場を近似的にバランスさせるために追加の方程式を導入する必要があります.
ただし, アセンブリ 操作では, オブジェクト間の隣接境界にいわゆる アイデンティティペア を自動的に作成することもできます. 各フィジックス内で, これらのペア境界に境界条件を適用できます. フィジックスインターフェースに応じて, さまざまな境界条件を使用できますが, すべてのケースで ペア連続性 条件を使用できます. この条件は, 境界を越えた場と流束の連続性を, 要素平均の意味で強制します. これは, 舞台裏で追加の方程式セットを追加することによって行われますが, ここでは詳しく説明しません. 要素が正確に整列していないため, 場と流束は点ごとに連続することはできません. これは欠点ですが, 隣接するドメインに異なるメッシュを持つことができるため, 利点があります. この交差流れ熱交換器の場合にこれがどのように役立つかを見てみましょう.
前に見たように, 流路に沿った温度変化は非常に緩やかです. 流れは層流で, 流路の断面は均一なので, 流れ場は流れの方向に沿ってほぼ不変であることもわかっています. したがって, 下の図に示すように, 流路に流れの方向に沿ってスイープメッシュを適用できます. 流れ方向で使用される要素が大幅に少なくなり, 以前のメッシュと比較して精度がわずかに低下するだけで問題のサイズが縮小されることがわかります.
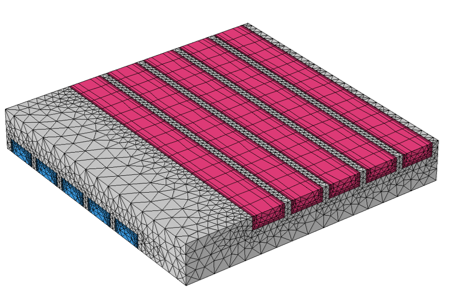
アセンブリメッシュでは, 流体流路内のスイープメッシュにより, 要素数が少なく, 細長いメッシュを作成できます.
さて, このメッシュを設定するために, 手動で行う必要がある手順がいくつかあります. まず, ジオメトリ シーケンス内で, 2 つの異なるオブジェクトを定義する必要があります. 最初のオブジェクトは金属部品, つまり流体が流れる固体です. 2 番目のオブジェクトは, すべての流体流れドメインの組み合わせです. つまり, ジオメトリ シーケンスのブール演算 ユニオン によって作成された, 複数の異なるドメインで構成される単一のオブジェクトです. フォームアセンブリの最終処理操作を有効にするには, これらのドメインが重複していないことを確認する必要があります. そうすることで, ソフトウェアはこれらのオブジェクト間のすべての対向面をアイデンティティペアとして自動的に認識します.
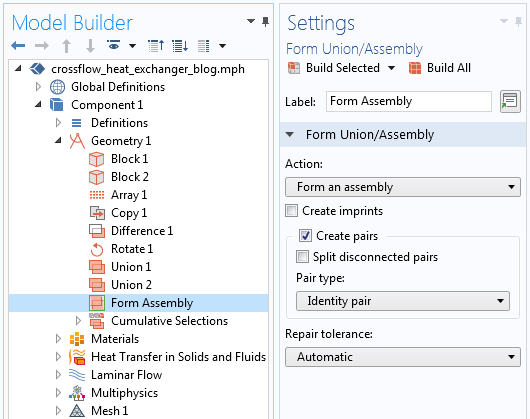
アセンブリのジオメトリの最終処理により, アイデンティティペアが自動的に作成されます.
次に, 固体と流体の伝熱インターフェース内で, ペア連続性境界条件を追加する必要があります. 隣接するオブジェクトは 2 つ (固体とすべての流体ドメイン) しかないため, この条件は 1 つの 同一境界ペアにのみ適用する必要があります. 物理的特性に対するその他の変更は必要ありません.
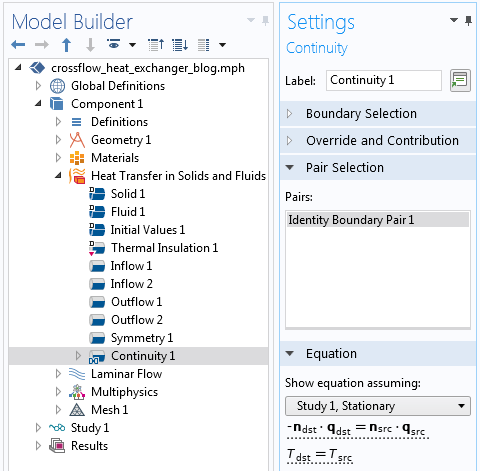
ペア連続性は, 場の連続性を強制し, 流束のバランスをとる境界条件です.
最後に, メッシュシーケンスを手動で変更する必要があります. デフォルトのメッシュシーケンスでは, ペア境界の合わせ面の要素がコピーされますが, これを無効にして, 流れ流路の長さに沿って引き伸ばされたスイープメッシュを適用します. この方向では解がかなり緩やかに変化することがわかっているため, 変更は正当化されます. 前に示した自動生成されたメッシュと比較して, メッシュにその他の大きな変更は加えられません.
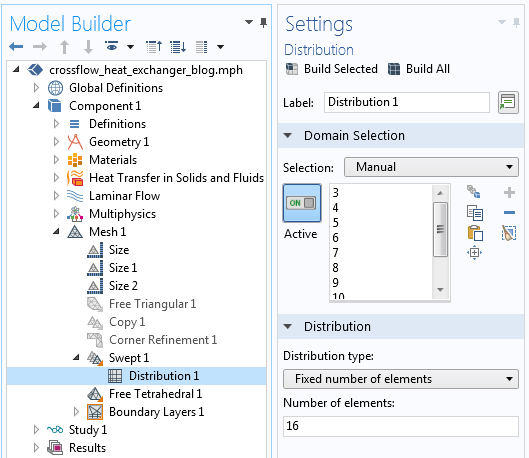
流路内の流れ方向に沿った要素の数を制御するために使用されるメッシュシーケンス.
温度場と温度場の差が以下にプロットされています. スイープメッシュを使用したモデルは当然異なります. この場合, 温度場は, 前のケースと比較して, 一部の領域で約 2°C 異なります. この差は, 主にインターフェース全体のメッシュの差によるものです. 追加のペア連続方程式によるものではありません. メッシュの細分化の限界では, 両方のアプローチは同じ解に収束します. アセンブリメッシュを使用する主な利点は, 比較的粗いメッシュから始めても妥当な結果が得られることです. これにより, 初期モデル開発の時間と計算リソースを節約できます.
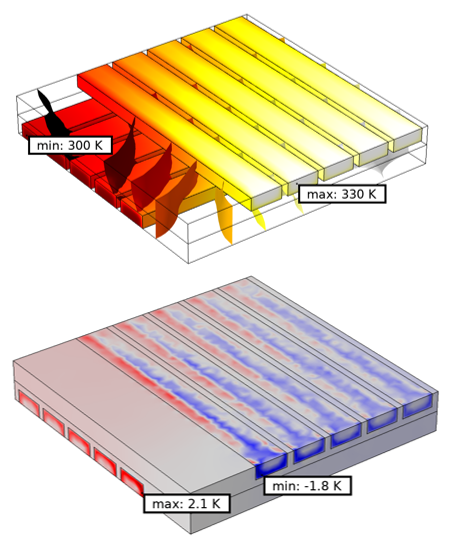
アセンブリメッシュを使用した温度場 (上) と, この温度場 (下) と既定のメッシュの差.
このジオメトリの場合, 別の方法でジオメトリを分割することもできます. 下の図に示すように, 流れ流路間の平面に沿ってモデルを 2 つのオブジェクトに分割できます. これで, 要素数をさらに減らすことができます. すべてのジオメトリがこの細分化に適しているわけではありませんが, このアプローチにより, 要素数をさらに減らすことができます.

別のメッシュ作成戦略では, 流体と固体の境界ではなく, 固体内にアイデンティティペアを導入します.
おわりに
ここでは, アセンブリメッシュがメッシュ要素の数を減らすのに便利な手法であることを説明しました. これは, 共役熱伝達問題に特に適しています. これらの問題には, スイープ メッシュに適した比較的均一な流れ流路が含まれることが多いためです. ここでは層流を含むモデルを検討しましたが, このアプローチは乱流問題にも有効です. ただし, この手法は予備モデル開発にのみ適用されることに注意してください. 通常, これらのモデルを合同メッシュのモデルと比較して検証し, もちろんメッシュの改良研究を常に実行する必要があります. 主な利点は, 予備分析をより迅速に実行できることです.
アセンブリメッシュ機能を使用したモデルはここからダウンロードできます:



コメント (0)