
今回は, 非線形問題を解くための完全連成アプローチと組み合わせて使用される COMSOL Multiphysics® ソフトウェアのモデルにゴール探索方程式をご紹介します. このアプローチは, 以前に紹介した分離アプローチよりも計算コストが高くなりますが, 堅牢性の点でいくつかの興味深い利点があり, COMSOL® ソフトウェアのコアの強みの1つを強調しています.
背景
分離ソルバーへのゴール探索の導入に関する以前のブログで説明したように, 特定の出力が達成されるように,モデルへの入力を更新する方法を定義する追加のグローバル方程式でマルチフィジックスモデルを拡張できます. このアプローチにより, 分離解法アプローチを利用して, 問題の一部を次々に求解し(さまざまなフィジックスを求解し), グローバル方程式を介して入力を更新できます.
このアプローチは非常に計算効率が高いですが, 分離ソルバーを使用しているため, 問題の基礎となる物理学の知識を使用して構築する必要があるアドホック更新方程式に依存しています.
ここでは, ソフトウェアが導関数をシンボリックに計算できるようにする方程式に基づいて, 入力の方程式が更新される代替アプローチを紹介します. このアプローチは, はるかに堅牢で一般的ですが, 計算コストがかかります. まず, このやり方を実装する方法を見てから, 相対的なメリットについて説明しましょう.
ここでは, 前に検討したのと同じ例を見ていきます. これは, 介在物のある媒体に適用された2つの電極のジュール加熱問題です. 材料の電気伝導率と熱伝導率は, 温度に対して非線形です. このモデルの目的は, 3ワットが介在物内で消費されるように, 上部電極と接地電極の間の電位差を調整することです.
完全連成ソルバーによるゴール探索を導入
以前のブログと同様に, これは グローバル方程式 を介して実現できますが, 今回は影響を受けるフィジックス内に グローバル方程式 を追加します. ただし, 前者の場合, この追加の方程式は, 個別の分離ソルバー反復内でアドホックスケーリングを使用して適用されるポテンシャルを更新することを思い出してください. ここでは, 影響を受けるフィジックスと同時に解かれたときにヤコビ行列に項を与える方程式を使用します.
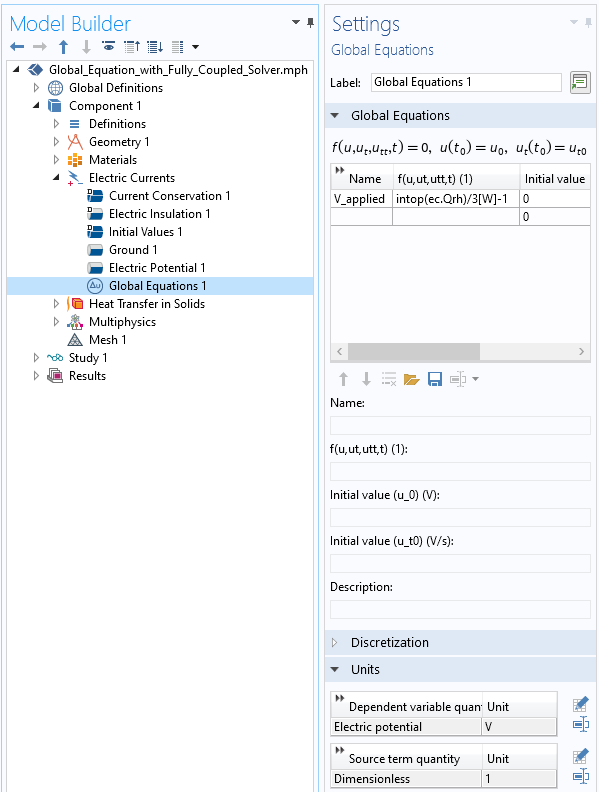
フィジックスインターフェース内でのグローバル方程式の導入
前の例を変更して説明しましょう. 印加電位 V_applied の グローバル方程式 を導入する必要がありますが, 電位の方程式と同時に満たされ, 解かれる方程式が必要になります. そのために, 電流 フィジックス内に グローバル方程式 機能を追加します. 求解点でゼロに等しくする残差方程式を入力していることに注意してください. 入力する方程式は次のとおりです.
intop(ec.Qrh)/3[W] – 1
ここで, intop() は, 含まれる領域に対して定義された 積分演算子 です. この方程式の無次元化にはいくつかの利点があることが後でわかります. 書き直すと, これは次と同等です.
intop(ec.Qrh) = 3[W]
これは次のように読み取ることができます. 含まれる領域における損失が3ワットに等しくなるようにV_appliedの値を計算します. この残差方程式が何を表すかを書き出すこともできます.
ヤコビアン寄与を計算するとき, モデル内のすべての未知数に関して, これのシンボリック導関数を取ります. 調べてみると, 次のことがわかります.
一方, 電位の導関数, \partial r / \partial V, および温度場に関する導関数,\partial r / \partial T, は非ゼロになります.
これは, グローバル方程式がヤコビアンの対角線にゼロを導入しますが, 対応する行に多くの非ゼロ項を導入することを意味します. これは, 非線形反復内で使用する必要がある線形系ソルバーの種類に影響します.
本当に興味深く有用な貢献であるのは, これらの追加の項です. これらの項は, グローバル方程式がゼロになるように V_applied を更新する方法を非線形ソルバーに指示します. つまり, ソフトウェアは V_applied への更新を自動的に把握します. (以前のアプローチでは, フィジックスの知識に基づいて独自の更新方程式を作成する必要があったことを思い出してください.)
非ゼロ勾配の導入
ただし, これらの追加条件にはコストがかかります. それらは, グローバル方程式と電位方程式を同時に解く必要があります. また, 非対角項と対角にゼロの両方が導入されるため, 電位場とグローバル方程式を解く場合は, 完全連成アプローチで直接線形系ソルバー を使用する必要があります. さらに, 上記の導関数は初期条件で非ゼロである必要があります. そうでない場合, ヤコビアンの行全体がゼロになります. この場合, 指定された初期値で電位にゼロ以外の勾配がなければならないという点で, これは少し重要であることがわかります.
電位にゼロ以外の勾配を導入する方法は2つあります. 最も簡単な方法は, 以下のスクリーンショットに示すように, 電流 フィジックスで空間的に変化する初期条件を指定することです. これは, 少なくともこの場合は簡単に実行できますが, 非物理的な初期値を導入するため, 常に機能するとは限りません.
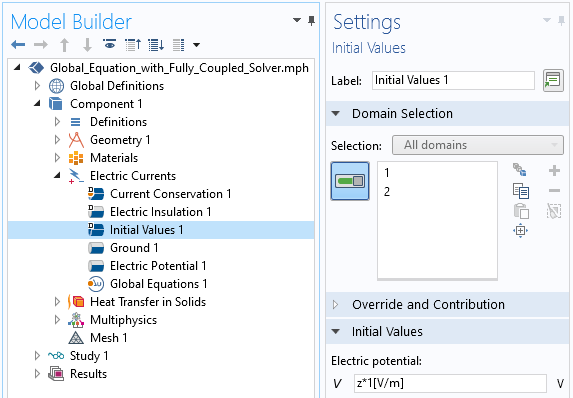
電位場にゼロ以外の勾配をもたらす初期値を電流フィジックスに導入する
より洗練されたアプローチは, 方程式を解く V_applied の グローバル方程式 の変分を導入することです.
V_applied/1[V] – 1
この方程式は,V_appliedを 1 [V]に等しく設定するだけで, ソフトウェアは連立方程式を解き, 一貫した電位場を計算します. これが, 無次元化された残差方程式があると便利な理由であることに注意してください. これは, 以下のスクリーンショットに示されています.
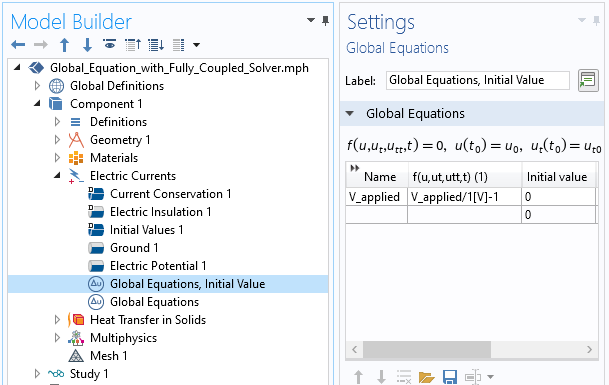
初期値を見つけるための追加のグローバル方程式の導入
グローバル方程式のソルバー設定の調整
V_appliedのこの固定値を解くと, 元のグローバル方程式の使用に戻ったときに, この問題の解を初期値として使用できます. これは, スタディステップのモデル構成を変更するチェックボックスをオンにしてから, 2つのスタディステップ内で2つの異なるグローバル方程式 を有効/無効にすることで実現できます. つまり, 最初の解析ステップでは, V_applied を指定するだけで, 2番目のステップでは, 包含内に目的の散逸があるように V_applied が求解されます. これは, 以下のスクリーンショットに示されています.
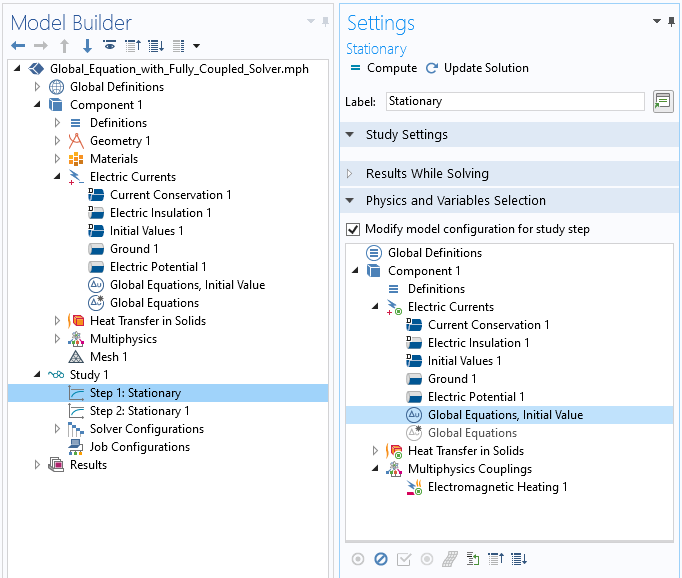
初期値のグローバル方程式 が解かれる最初のスタディステップのモデル構成を変更します. 2番目のステップでは, 反対の設定が適用されます
この2番目のステップでは, デフォルトのソルバー設定を調整する必要があります. 2つの選択肢があります.
- 問題全体に対して完全に連成されたアプローチを使用し, 直接ソルバーを使用します. これにより, ソルバー設定の変更は最小限で済みますが, 直接ソルバーを使用 して大規模な連立方程式を解くには, 大量のメモリが必要になります
- 分離ソルバーを使用しますが, グローバル方程式と電位方程式を1つのステップに結合します. これは, 自動ニュートンアプローチと直接ソルバーを使用して収束するように解かれます. 温度解は, 反復ソルバーを使用して分離された方法で求解できます. このアプローチでは, 設定をさらに変更する必要がありますが, 求解するために必要なメモリは少なくなります. この分離により, \partial r / \partial T 項が無視されることになり(存在する場合), 収束に悪影響を与える場合があることに注意してください. これらの設定の変更は, 以下のスクリーンショットに示されています.
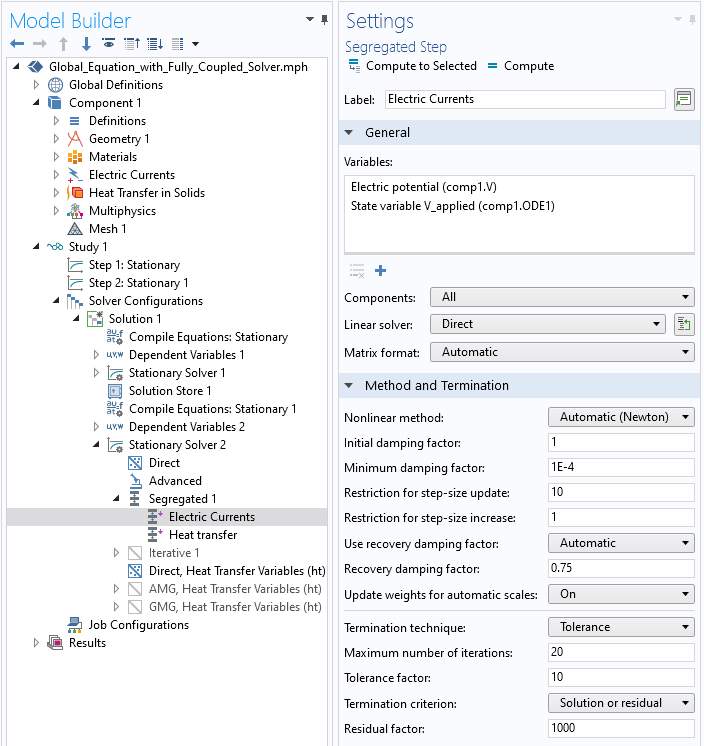
グローバル方程式と電位は, 直接ソルバーを使用して同時に解く必要があります
メモリ要件が高すぎる場合は, 最初のアプローチから始めて, 2番目のアプローチを試すことをお勧めします. 3Dモデルの場合, 直接ソルバーのメモリ要件は, 問題のサイズとともに非常に急速に増加することに注意してください. これが主な制限です.
結論
ここに示すアプローチは, プログラミングに頼ることなくGUI内のゴール探索の問題に対処するために使用できるいくつかのアプローチの1つです. 以前の投稿 で説明した, このクラスの問題を求解するための他のアプローチは次のとおりです.
- 最適化モジュールの使用
- パラメトリックスイープを使用し, おおよその目標値を手動で特定する
- 追加の更新方程式で分離ソルバーを拡張する
ここに示すアプローチの重要な利点は, メモリ要件が高いにもかかわらず, 迅速かつロバストに収束することです. この手法は, 各時間ステップでグローバル方程式が満たされる限り, 時間領域でも使用できることに注意してください.
このロバストで迅速な収束は, ヤコビ行列内の追加の項の結果であり, 高度に非線形な連成マルチフィジックス問題を求解するための COMSOL Multiphysics の長所を強調しています. この手法は, 前述の手法とともに, アナリストがツールベルトに組み込むための優れたツールです.


コメント (0)