
波動電磁気学の問題を解くとき, 境界が開いているドメイン, つまり, 電磁波が反射することなく通過する計算ドメインの境界をモデル化したい場合があります. COMSOL Multiphysics には, このためのいくつかの解決法があります. ここでは, 散乱境界条件と完全整合層を使用したドメインの切り取りについて説明し, それらの相対的な利点について解説します.
なぜドメインを切り取るのか?
自由空間におけるアンテナなどの放射物体のモデル化する必要があることがあります. その目的は, 深宇宙にある人工衛星に搭載されたアンテナをシミュレートするためかもしれませんし, 無響試験室に取り付けられたアンテナをシミュレートするためかもしれません.
無限の自由空間にあるアンテナ. モデル化したいのはアンテナの周りの小さな領域だけです.
このようなモデルは, RFモジュールまたは波動光学モジュールの電磁波 (周波数領域) 定式化を使用して構築することができます. これらのモジュールは, 有限要素法を用いてマックスウェル方程式の周波数領域形式を解くための同様のインターフェースを提供します. (これらのモジュールの主な違いについては, 私の以前のブログ“計算電磁気学モデリング, どのモジュールを使うべきか ?”をご参照ください.)
このブログでは, 電磁波がx-y平面上を伝搬し, 電場がz方向に偏光している2次元の問題のみを見ていきましょう. さらに, モデリングドメインは純粋な真空であると仮定すると, 周波数領域のマックスウェル方程式は以下のようになります:
ここで, E_zは電場, \mu_r = \epsilon_r = 1は真空中の比透磁率と比誘電率, k_0は波数です.
有限要素法で上記の方程式を解くには, 有限サイズのモデリングドメインと一連の境界条件が必要です. 放射に対して透過的な外側に沿った境界条件を使うのが理想的です. そうすることで, 切り取ったドメインを自由空間の合理的な近似とすることができるからです. また, モデルサイズを小さくすることで計算コストを削減できるため, この切り取りドメインはできるだけ小さくする必要があります.
次に, COMSOL Multiphysics シミュレーション環境で使用できる, モデリングドメインを切り取るための 2 つのオプション, 散乱境界条件と完全整合層について説明します.
散乱境界条件
波動型問題に対して定式化された最初の透明な境界条件の一つは, ゾンマーフェルト輻射条件であり, 2次元場に対して次のように記述できます:
ここで, rは動径座標です.
この条件は, 我々のモデリング領域の境界がソースから無限に離れているとき, 正確に非反射となりますが, もちろん無限に大きなモデリングドメインは不可能です. したがって, ゾンマーフェルト条件を厳密に適用することはできませんが, 合理的な近似を適用することはできます.
ここで, 次の境界条件を考えてみましょう:
この条件とゾンマーフェルト条件の類似点がよくわかります. この境界条件は, より正式には一次散乱境界条件 (SBC)と呼ばれ, COMSOL Multiphysics で実装するのは簡単です. 実際には, 複素数値の係数を持つロビン境界条件に他なりません.
この境界条件に従ってゼロから実装された2D波動方程式の例を見たい場合は, 回折パターンのモデル例をご覧ください.
さて, この条件には重大な制限があります. それは, 入射輻射が境界に対して正確に垂直に入射している場合にのみ, 非反射となることです. 非垂直入射でSBCに入射した波は, 部分的に反射されます. さまざまな入射角で一次SBCに入射する平面波の反射係数を以下にプロットします.
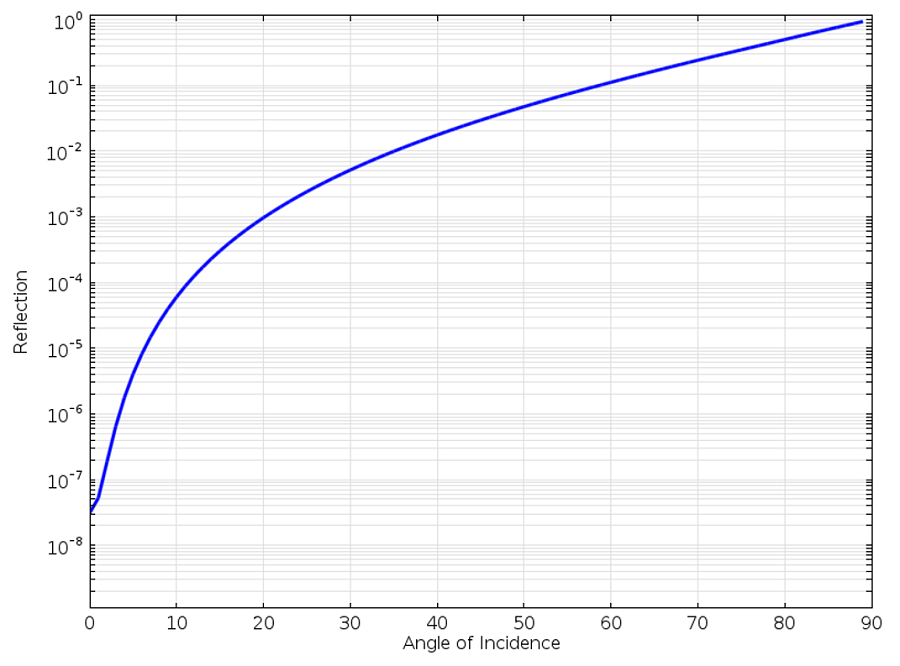
入射角に対する一次SBCでの平面波の反射.
上のグラフから, 入射する平面波がかすめ入射に近づくにつれて, 波はほぼ完全に反射されることがわかります. 入射角が60 °の場合, 反射率は約10%であり, より良い境界条件が必要であることは明らかです.
COMSOL Multiphysics には (バージョン 4.4 以降) 2 次 SBC も含まれています:
この方程式には, 境界に沿って電場の 2階接線微分2 番目の項が追加されます. これは, COMSOL ソフトウェアアーキテクチャー内で実装することも非常に簡単です.
1次SBCと2次SBCの反射係数を比較してみましょう:
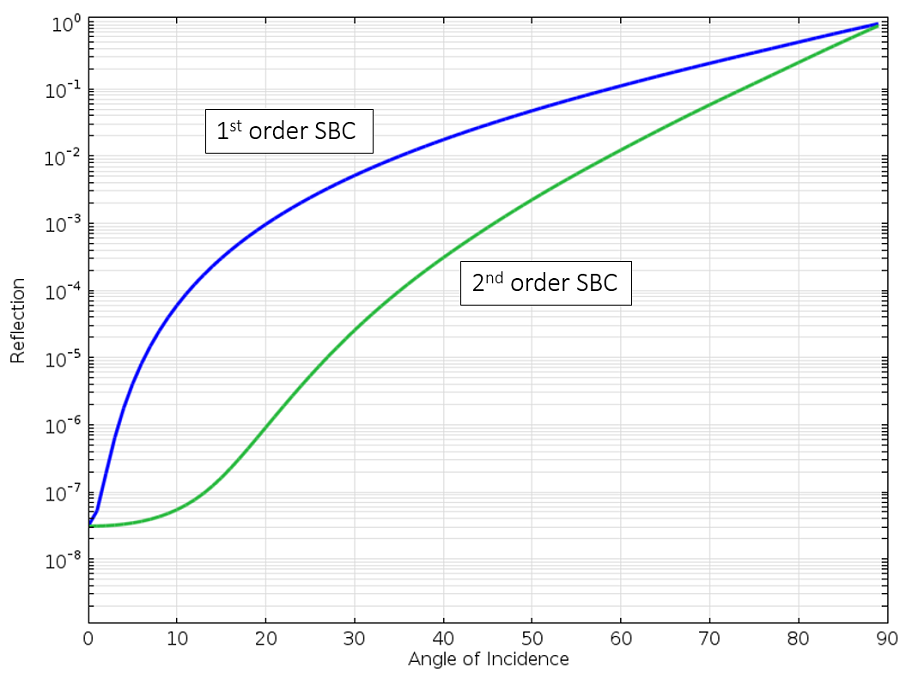
入射角に対する1次および2次SBCでの平面波の反射.
2次SBCの方が一様に優れていることがわかります. 反射が10%になる前に, 約75 °の入射角に達することができます. これで改善はされましたが, まだベストではありません. 次に, 境界条件から移って, 完全整合層を見てみましょう.
完全整合層
まず, 無響試験室内のアンテナなどの状況をシミュレートしようとしていることを思い出してください. 無響試験室とは, 壁に放射を吸収するピラミッド型のくさびがあり, 反射された信号を最小限に抑える部屋です. これはアナロジーですが, 実際に完全整合層 (PML) は境界条件ではなく, すべての発信波を吸収する, モデルの外側に沿って追加するドメインです.
数学的に言えば, PMLは単に異方性で複素数値の誘電率と透磁率を持つドメインです. これらのテンソルの完全な導出のサンプルについては, 電磁場の理論と計算をご参照ください. PMLは理論的には無反射ですが, 数値離散化 (メッシュ) により若干の反射を示します. この反射を最小にするために, 材料特性の異方性と一致するメッシュを使用したいと考えます. 2D円形ドメインと3D球形ドメインについて適切なPMLメッシュを以下に示します. 直交および球面PMLとその適切な使用法については, マニュアルでも説明しています.
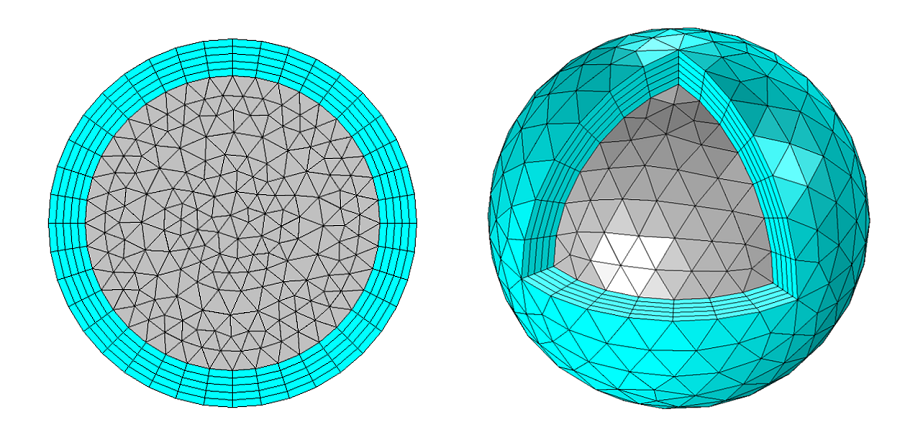
2D および 3D 球面 PML に適切なメッシュ.
COMSOL Multiphysics 5.0 では, こちらのビデオで紹介しているように, フィジックス制御メッシュを使用して, 3D問題に対してこれらのメッシュを自動的に設定することができます.
ここで, SBCと比較して, 入射角に関するPMLからの反射を見てみましょう:
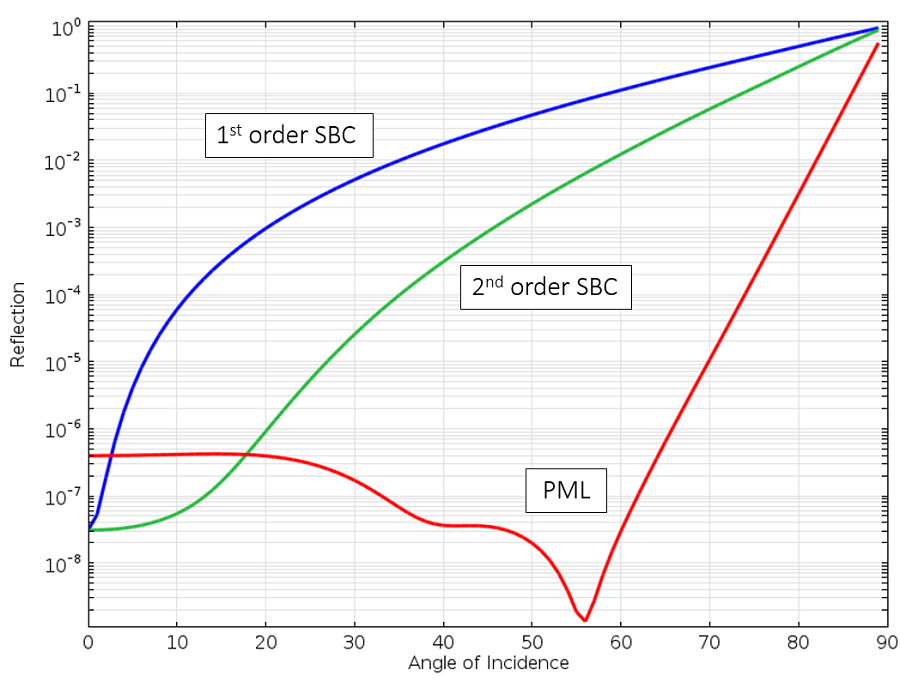
1次, 2次SBCとPMLでの平面波の入射角に対する反射.
PMLは, 最も広い範囲で最も反射が少ないことがわかります. 波が境界とほぼ平行に伝搬している場合はまだ反射がありますが, そのようなケースは実際にはかなり稀です. PMLのもう1つの特徴は, ここでは詳しく説明しませんが, 伝搬波だけでなく, あらゆるエバネッセント場も吸収することです. つまり, 物理的な観点からは, PMLはほぼ完璧な吸収性を持つ物質と考えることができるのです.
では, どのオプションを使うべきか?
PMLがここで説明したアプローチの中で最も優れているのは明らかです. しかし, PMLはSBCに比べてより多くのメモリを消費します.
したがって, モデリングプロセスの初期段階で, もう少し計算量の少ないモデルを構築したい場合には, 2次SBCが良い選択肢となります. また, SBCでの反射が, 確実に問題の結果に大きな影響を与えない場合にも使用できます.
現在のところ, 旧バージョンとの互換性を考慮して 1 次 SBC がデフォルトとなっていますが, COMSOL Multiphysics のバージョン 4.4 以上では 2 次 SBC を使用することをおすすめします. ここでは平面波形式の SBC のみを紹介しましたが, 円筒波形式および球面波形式 (3D) の 1 次および 2 次 SBC も利用可能です. これらはメモリ使用量は少ないですが, いずれもPMLに比べて反射が大きくなります.
SBCとPMLは, 事前によく分からない開いた境界には適切な条件です. 一方, 導波路を表す境界のように, 場が特定の形式を持つことが分かっている開いた境界をモデル化したい場合は, ポート境界条件と集中ポート境界条件がより適切です. これらの条件については, 今後のブログで説明します.



コメント (0)