
トレビュシェット は, 中世やファンタジー世界を舞台にした映画などで見たことがある大型の攻城兵器です. この兵器は, 位置エネルギーを運動エネルギーに変換し, 発射物を長距離にわたって投げつけるという発想に基づいています. 一見シンプルですが, トレビュシェットは複雑な力学システムです. このブログでは, マルチボディダイナミクスモジュールを用いて, カウンターウェイトトレビュシェットの簡略化されたモデルを構築し, その設計上の特徴をいくつか検証します.
War Wolf: 究極の攻城兵器
トレビュシェットは, スイングアームを用いて標的に向けて発射物を投げつける長距離兵器です. トレビュシェットといえば, 城壁に巨石を投げつけて崩すというイメージが一般的ですが, Greek fire を投げつけて, あらゆる大混乱を引き起こすためにも使われてきました. トレビュシェットは, 映画やテレビ番組にも登場しています. 例えば, The Return of the King (2003), Marco Polo (2014–2016), Monty Python and the Holy Grail (1975) では, 城壁の中から牛が放たれ, 何も知らないアーサー王に向かって飛んでいきました!
ノンフィクションで歴史的にも有名なトレビュシェットの一つに, War Wolf (当時のイギリス兵からは “Ludgar” と呼ばれていました) があります. 1304年, スコットランド征服を企む遠征のさなか, エドワード1世はスターリング城を包囲し, 技師たちに巨大なトレビュシェットの建造を命じました. War Wolf は史上最大のトレビュシェットであり, 約150キログラムの巨石を200メートル以上も飛ばしたと伝えられています. 
War Wolf の小型レプリカ. スイングアームの先端に岩石を固定するスリングを備えたカウンターウェイト式トレビュシェット. 画像提供: Ron L. Toms. CC BY 3.0 ライセンス, Wikimedia Commons 経由.
この種の大型トレビュシェットは通常, 発射物の約10倍の重量のカウンターウェイトを備えており, War Wolf のカウンターウェイトは約1.5トンにもなります. War Wolf の攻撃を生き延びる見込みが低いため, 城内にいたスコットランド軍は降伏を申し出ました. しかし, 国王は新しいトレビュシェットを試してみたかったため, これを受け入れませんでした. 国王はスコットランド軍を城内に留まらせ, 包囲を再開しました. War Wolf はその真価を証明し, 残りは言うまでもなく歴史の通りです.
トレビュシェットの動作原理は単純だ. カウンターウェイトを上げ, トレビュシェットをコッキングする. トレビュシェットが発射されると, カウンターウェイトが下がり, システムの位置エネルギーが運動エネルギーと位置エネルギーの組み合わせに変換される. 弾丸は揺動運動し, 軌道上の適切な位置で放たれる. これは, スリングの一端がスイングアームの先端から外れることで起こる.
カウンターウェイトトレビュシェットのマルチボディ解析の実行
ここでは, マルチボディダイナミクスモジュールと COMSOL Multiphysics® ソフトウェアバージョン 5.3 を使用して, 基本的なトレビュシェットの計算モデルを構築します.
このモデルでは, 以下の仮定と物理的寸法を採用しています.
- すべてのコンポーネントは剛性であると仮定 (スリングを含む)
- すべてのヒンジジョイントは摩擦がないと仮定
- ペナルティ剛性によって, 発射体が地面をすり抜けて落下するのを防止
- キャリッジを表す長さ L5 = 3.5 m の垂直梁は固定
- カウンターウェイトの質量 (M = 2000 kg) と発射体の質量 (m) の比は 100
- カウンターウェイトは長さ L4 = 1 m の梁から吊り下げる
- スイングアームの全長は 6 m で, L1 = 1 m
- スリングの長さは L3 = 3 m
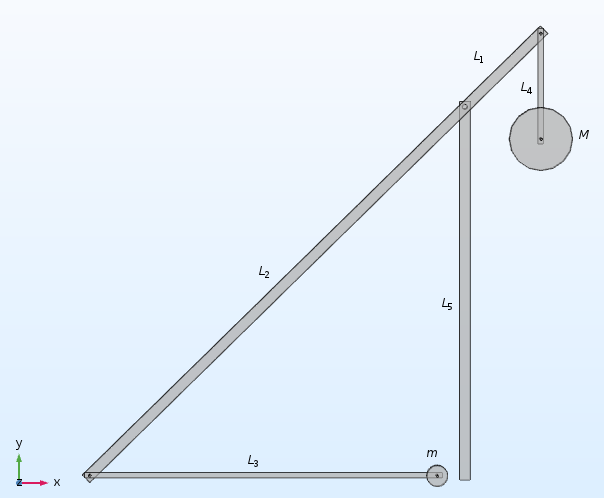
カウンターウェイトトレビュシェットモデルの概略図.
投射物がスイングアームによって振り回されると, 速度が変化する複雑な運動をします. 投射距離を最大限に伸ばすようにトレビュシェットを設計する場合, 次のような疑問が生じます. 投射物の軌道上のどの時点で投射すべきでしょうか? 初等力学によれば, 空気抵抗と発射体が投下される地面からの高さを無視すれば, 発射体の投下距離 s (正の x 方向に測定) は次のように表すことができます.
ここで, v0 と α はそれぞれ発射時の速度と角度, g は重力加速度です.
したがって, 最大投下距離を求めることは, s を最大化する v0 と α の組み合わせを求めることと同じです. 直感的には, 投下角度は α = 45° であると考えるかもしれません. これがトレビュシェットモデルにも当てはまるかどうか見てみましょう.
下のアニメーションは, トレビュシェットが発射される様子を示しています. s という値は投射物の軌道に沿って表示されており, この軌道上の特定の地点で投射物を投射した場合に得られる投射距離を表しています.
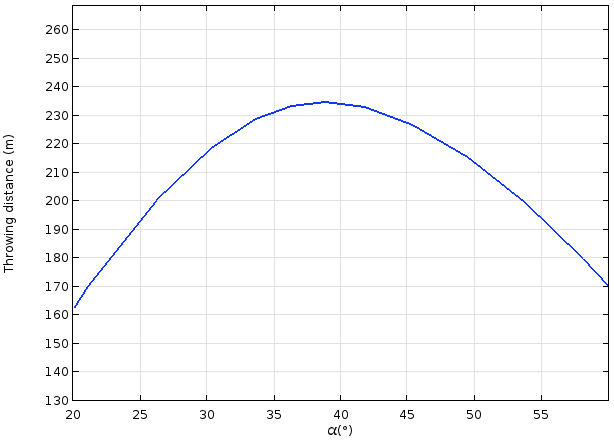
以下の結果では, 投擲距離が発射角度 α の関数としてプロットされています. 投擲距離が最大になるのは, 発射体が α ≈ 38° で発射された場合です. プロットから, この最適値から 5° 程度のずれがあっても, 投擲距離への影響は数メートルにとどまることがわかります. つまり, 発射角度がおおよそ正確であれば, トレビュシェットは意図したとおりに機能します.
では, パラメトリックスイープを用いてスリングの長さを ±10% 変更した場合に何が起こるかを見てみましょう. 下のグラフは, 得られる最大投擲距離がスリングの長さに大きく影響されることを示しています. 中世の王様のためのトレビュシェットを設計するなら, この設計パラメーターに注意を払う必要があります.
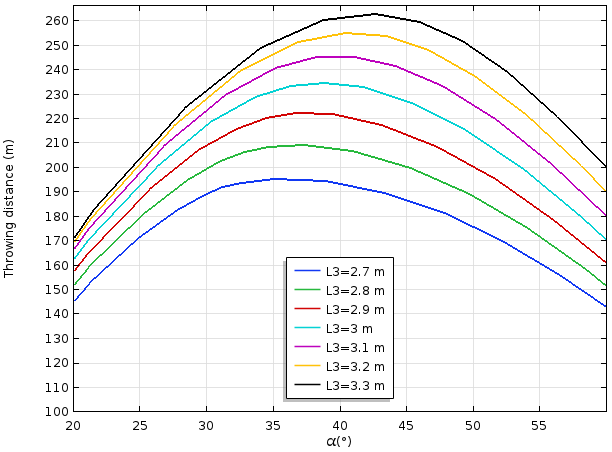
パラメトリックスイープを使用すると, モデル内の他の物理的な長さを変更した場合の影響を簡単に調べることができます (一貫性を保つためにカウンターウェイトの高さは固定したまま). アプリケーションギャラリからモデルファイルをダウンロードして, ご自身でお試しください.
まとめ
このブログでは, マルチボディダイナミクスモジュールを使用して, カウンターウェイトトレビュシェットのシンプルなモデルを作成できることを示しました. マルチボディダイナミクスモデリングについてさらに詳しく知りたい方は, 以下のブログをご覧ください:
War Wolf が Ludgar とも呼ばれていたのはなぜでしょうか? どうやら, フランス語の Loup de Guerre (wolf of war) という名前がイギリス兵にとって長すぎるため, “Ludgar” に短縮されたようです.



コメント (0)