
COMSOL Multiphysics®ソフトウェアのバージョン6.2のリリースをはじめに, 電気的分散モデリング機能が, 時間領域と周波数領域の両方のモデリングをサポートする電流インターフェースに拡張されました. この機能は, 絶縁体や生体組織を含む幅広い材料の正確なモデリングに特に重要です. ここでは, 分散とは何かを簡単に解説し, COMSOL モデルに分散を含める方法と, 分散が重要である理由についてご説明します.
背景
心筋アブレーション, エレクトロポレーション, 神経刺激など, 生体組織に印加される高速電流パルスをモデル化する際には, 電気絶縁体だけでなく, 組織の分散性を考慮する必要があります.
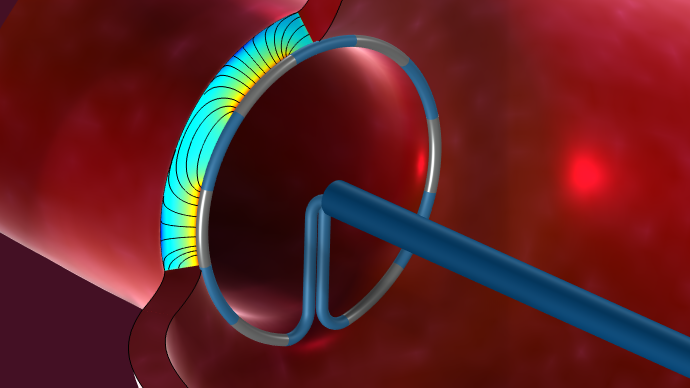
すべての材料は電気分散性であり, 比誘電率は励起周波数によって変化します. 誘電率は, 電場下で材料がどのように応答するか, つまり分極するかを示す尺度です. この応答の大きさは, 材料内の原子や分子, およびそれらの構造が異なるため, 周波数によって変化します. これはまた, 材料が時間的に変化する信号にさらされたときに, どれだけの電気エネルギーが熱に変換されるか, あるいは失われるかを示す尺度でもあります. このような損失は, 原子や分子が時間変化場の中で振動する際の相対運動によって生じます. 周波数領域で作業する場合, 比誘電率は複素数\epsilon_r =\epsilon_r^{‘}- i \epsilon_r^{”}で表され, 実数成分と虚数成分は Kramers–Kronigの関係式で表されます. このような2つの分散曲線が下図に示されており, それぞれ絶縁材料と生体組織を表しています. 前者は比較的単純な曲線で, 広い周波数帯域にわたって特性がほぼ均一であるため, 必ずしも分散を考慮する必要がないことがわかります. 一方, 特性に大きなばらつきがある周波数帯域も必ず存在するため, その場合は分散を考慮する必要があります.
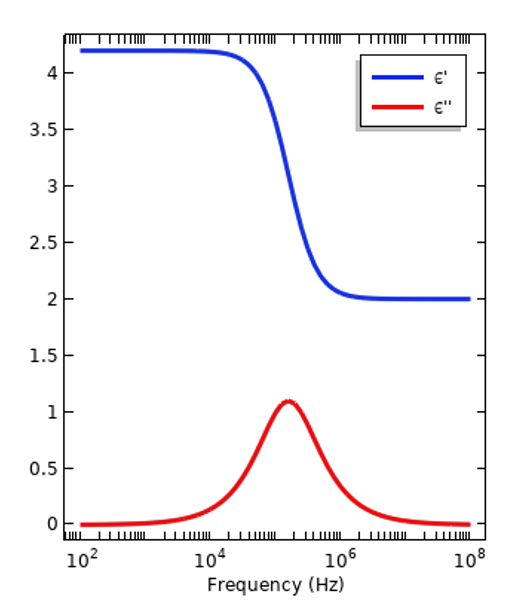
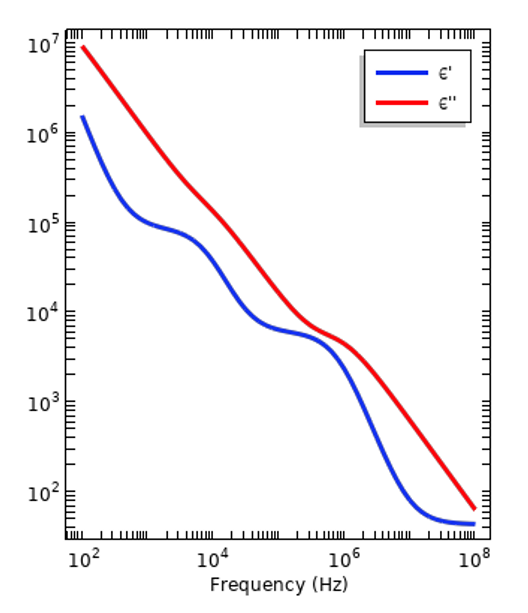
絶縁体 (左) とヒト組織 (右) の代表的な分散曲線. 比誘電率の実数値成分と虚数値成分の大きさがプロットされています.
これらの周波数依存損失に加えて, 静電場における電気的損失もあり, これらは直流電気伝導率 (DC) によって定量化されます. すべての材料はある程度の直流導電性がありますが, これは非常に小さい場合があります. これは分散損失とは別の損失メカニズムです. メカニズムに関係なく, すべての材料損失を全導電率\sigma_{tot} =\sigma_{DC} + 2\pi f \epsilon_0\epsilon_r^{”}で表すと便利です. これは, 同じ2つの材料について以下にプロットされています. ただし, 周波数依存の導電率は, DC成分を含まない\sigma(f) = 2\pi f \epsilon_0\epsilon_r^{”}として表すこともでき, \sigma_{DC}は別個に記述することも可能であることにご注目ください.
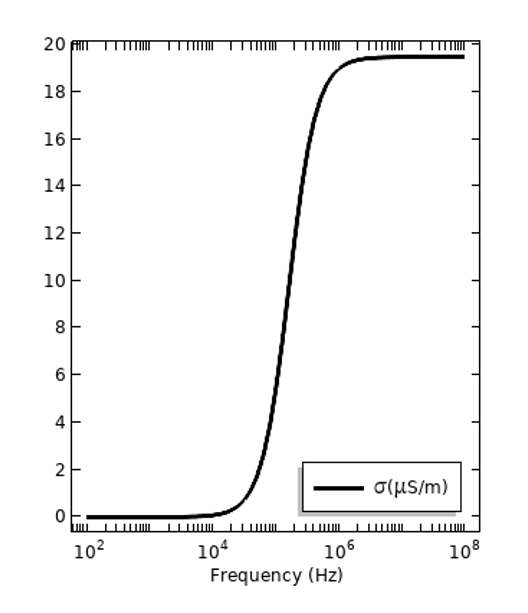
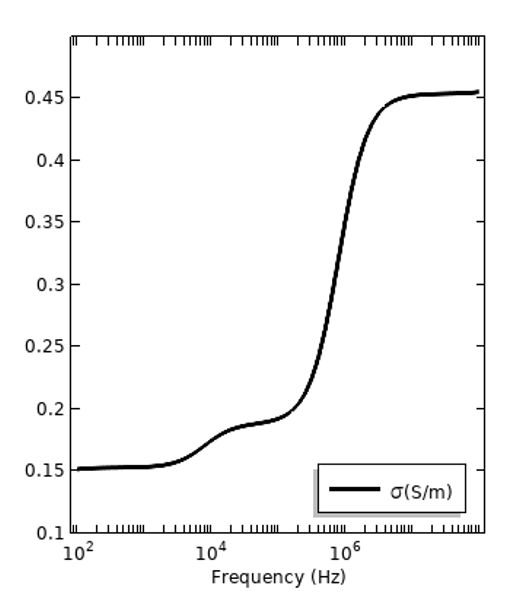
全導電率で表された同じ2つの材料の損失. DC伝導率は分散損失への寄与として示されています.
材料特性は実験的に決定されますが, 実験データには不確実性があり, Kramers–Kronig関係を満たさないため, 非因果的なモデルになってしまうので, 実験データを直接使用することは望ましくありません. その代わりに, すでにKramers–Kronig関係を満たしている関数をデータに当てはめ, その当てはめた関数の係数を使用して材料の挙動を記述します. 現在, ソフトウエアは多極デバイモデルをサポートしています. このモデルは, 極の数Nを入力とし, 各極mは緩和時間\tau_mと比誘電率寄与\Delta \epsilon_r_mを持ち, これらから複素値の誘電率を次のように定義します.
ここで \epsilon_\inftyは, 低周波極限\epsilon_\infty \rightarrow \epsilon_{rS}-\Sigma \Delta \epsilon_r_mまたは高周波極限\epsilon_\infty \rightarrow \epsilon_{rS}のいずれかに基づいています. さらに, 緩和時間は, Volger-Fulcher, Arrhenius, Williams-Landel-Ferry, Tool-Narayanaswamy-Moynihanのいずれかのシフト関数, またはユーザー定義のシフト関数を使用して, 温度の変化により任意にシフトすることができます.
または, 誘電率の実数成分と虚数成分の実験データがあり, それにデバイモデルをフィッティングしたい場合, COMSOL® バージョン 6.2 の部分分数フィッテイング機能を使用して行うことができます. この機能の使用方法については, ラーニングセンターの記事“デバイ分散モデルの実験データへのフィッティング”をご参照ください.
電流インターフェースの使用
電流モデルに分散を含めるには, わずか数ステップで済みます. まず, 電流保存ドメイン機能を追加し, 関連するドメインに適用します. その機能内で, 材料タイプを固体に設定します. これは, 流体が変形しないと仮定して, 流体のモデル化にも使用できます.
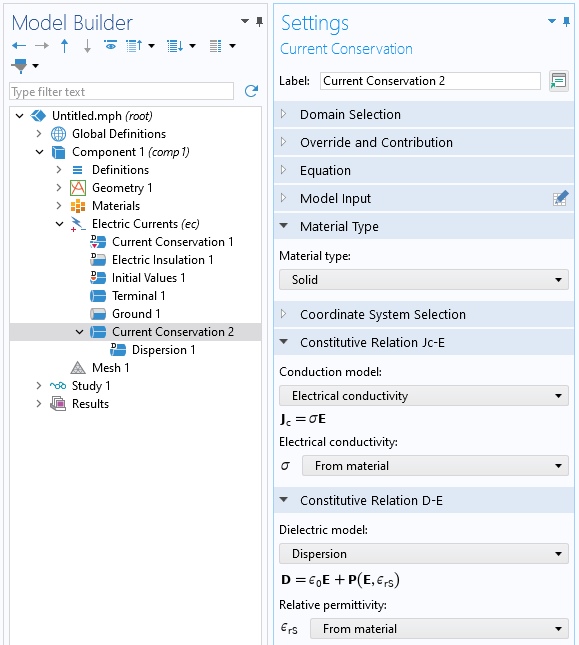
分散誘電モデルを選択できる電流保存機能.
誘電モデルのオプションを分散に変更すると, 追加のサブ機能が表示されます. この機能では, 以下のスクリーンショットに示すように, 多極子デバイモデルの分岐と限界挙動が入力されます. 極や分岐を入力する代わりに, 損失正接, 中心周波数, 帯域幅を入力とする定損失正接モデルを使用して緩和データを指定することもできます. これらの入力から, ソフトウェアは極の数, 緩和時間, 比誘電率の寄与を自動的に決定します. 極が1つしかない, より単純なデバイモデルを使用することも可能です. 緩和時間のシフトを引き起こす熱効果は, 熱効果設定でオプションで有効にすることができます.
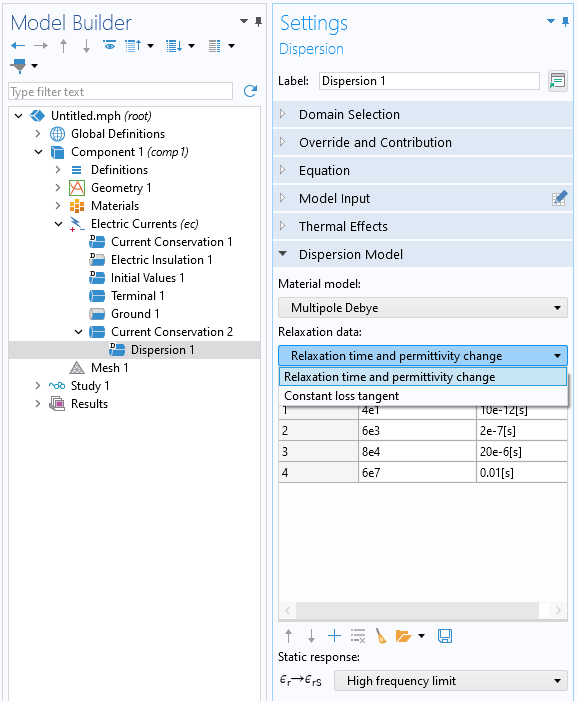
多極デバイモデルの分岐が入力され, 限界挙動が指定される分散サブ機能.
結果を見る
分散が, 周波数領域で動作する平行平板コンデンサーのような単純な系の応答にどのような影響を与えるかを調べ, 内部に挟まれた2つの異なる材料を試してみることができます. 以下のプロットから, インピーダンスの実数成分と虚数成分が周波数によってどのように変化するかを見ることができます.
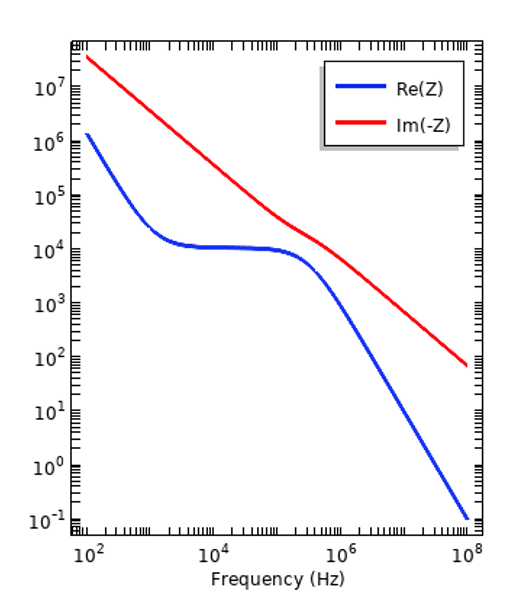
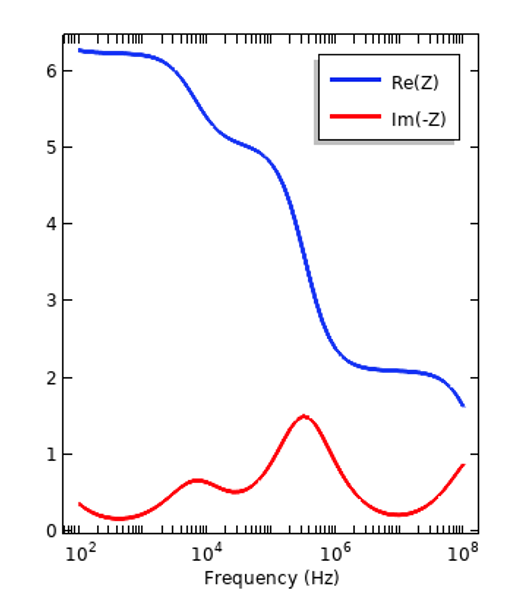
内部に絶縁体 (左) と組織 (右) のサンプルを備えた平行平板コンデンサのインピーダンス. インピーダンスの負の虚数成分がプロットされていることにご注目ください.
同じモデルを使用して, 同じ系の時間ドメイン励起の結果を調べることもできます. 周波数に対する応答の変化がより劇的であるため, ここではサンプル組織材料のみを見ていきます. 分散材料の設定は同じですが, このような系を励起するさまざまな方法を復習することをおすすめします. まず, 印加電流の平滑化されたステップでシステムを励起し, 10nsにわたって0-1Aまで上昇させ, 端子で感知された電圧をプロットすることによって100μsにわたる応答を計算します (下図参照). 結果は時間経過とともに対数スケールでプロットされます.
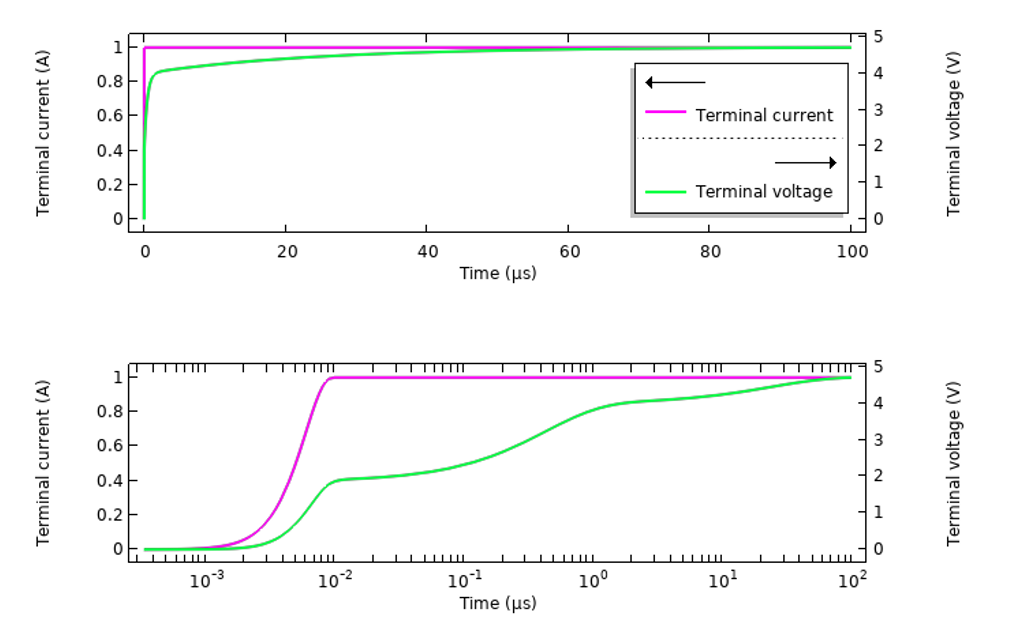
電流を印加したサンプル組織材料の経時的な過渡応答.
これらの結果を, 伝送線路に沿って伝搬する同様に平滑化ステップ電圧信号によって励起されるモデルと対比すると興味深いです. 以下の図は, 電流と電圧の測定値による応答を示しています. ここでプロットされた電圧信号は, 入射平滑化ステップ電圧信号と, 構造と材料からの反射信号の和であることにご注目ください. この総信号は, 分散材料に起因する時変挙動を示します.
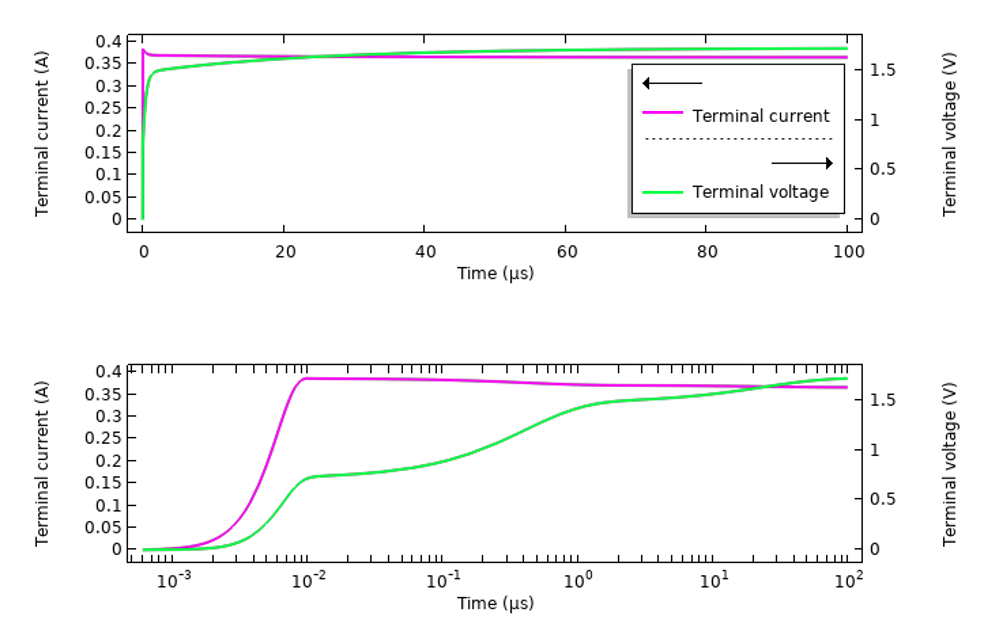
ステップ電圧信号により, 伝送線を介して励起されたサンプル組織材料の過渡応答.
おわりに
電流インターフェース内での電気的分散のモデリングが可能になり, 簡単に設定できるようになりました. この材料モデルは, 周波数領域と時間領域の両方のモデルにおいて, 損失だけでなく, 真の電気的応答をより正確に捉えます. この機能は, 多くの材料のモデリングに役立ちます.
電気的分散のモデリングは, 静電インターフェースを介してでも実行可能であり, バージョン6.0以降では, 主に損失性の圧電材料のモデリングを目的としています. さらに, より高い周波数でモデリングする場合のために, RFモジュールと波動光学モジュールには, 他の分散モデルが含まれています.






コメント (0)