
量子力学は, 特に 20世紀の最初の数十年間に, 現代物理学の時代を切り開きました. 私たちの現実の理解をこれほど大きく揺るがした理論は他にないと言っても過言ではありません. このブログでは, 量子力学のおそらく最も重要な正確な結果を見ていきます. 水素原子の基底状態と最初のいくつかの励起状態 – また, COMSOL Multiphysics® ソフトウェアを使用してこれらの結果を再現する方法について説明します.
量子力学と原子構造
原子の存在と安定性は, 正電荷を持つ原子核と負電荷を持つ電子の雲で構成されていますが, 古典物理学では説明できませんでした. 原子核の周りを回る電子のように, 加速度的に運動する荷電粒子は, 電磁波を発生させ, 徐々にエネルギーを失い, 必然的に電子は原子核に崩壊していくはずです. 量子力学は, 結合した電子はある一定のエネルギー値しか持たないことを証明し, 放射線によるエネルギーの漸減を禁止することで, この難問を解きました. これは数学的には定在波に似ています. 波は一値でなければならず, それはある一定の波長, すなわちエネルギーに対してのみ可能なのです.
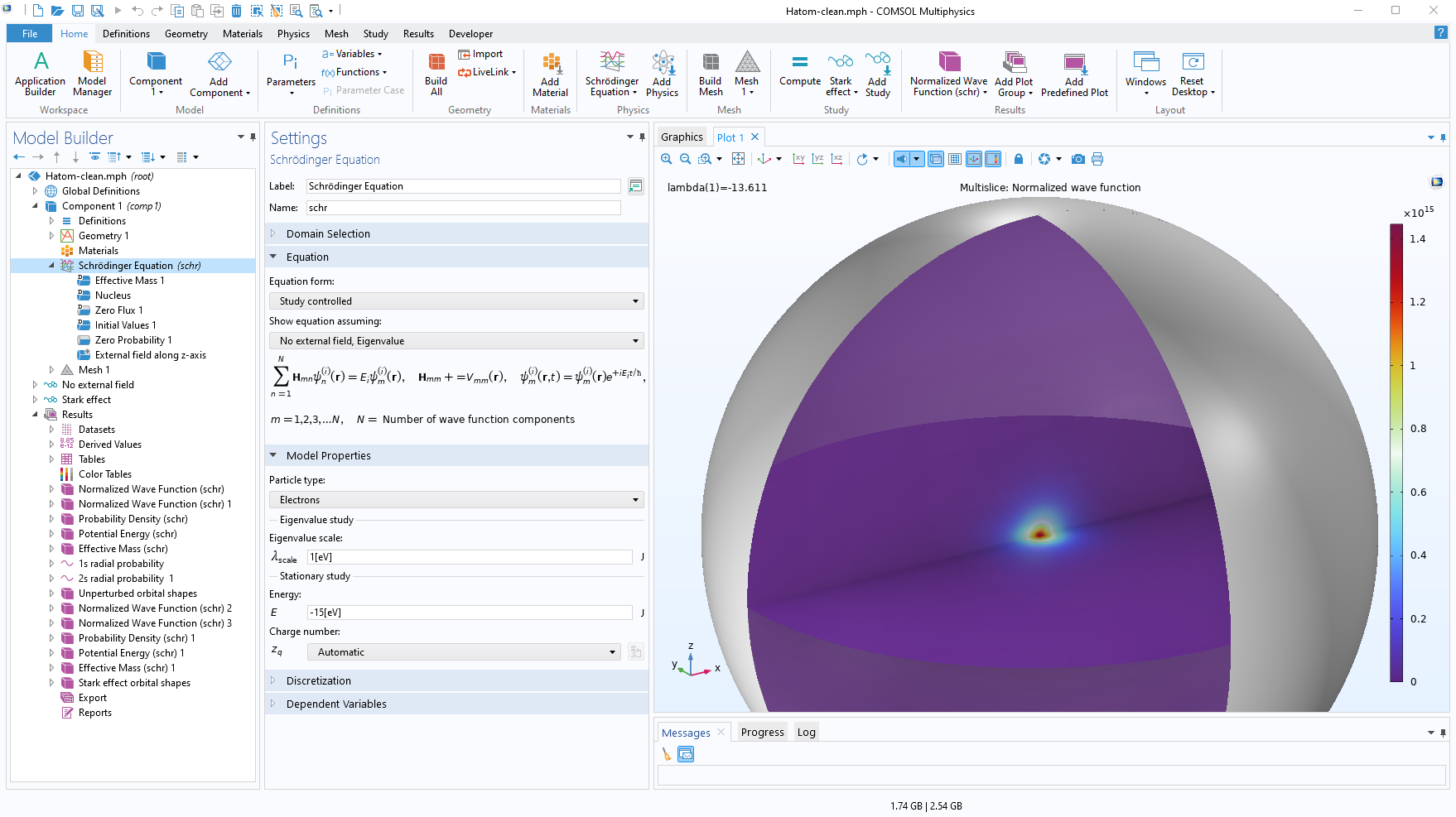 水素原子モデルを表示するグラフィックスウィンドウを備えた COMSOL Multiphysics® ユーザーインターフェース. これについては, 次のセクションで詳しく説明します.
水素原子モデルを表示するグラフィックスウィンドウを備えた COMSOL Multiphysics® ユーザーインターフェース. これについては, 次のセクションで詳しく説明します.
量子力学の力の初期の実証の 1 つは, 分光測定による水素の結果 (下記参照) の実験的確認でした. それ以来, 量子力学は物理学で最も検証された理論となっています.
多電子原子とは異なり, 単一電子を持つ 水素原子は, 非常に優れた性質を持っています. 時間に依存しないシュレーディンガー方程式 (TISE) で記述される近似:
ここで, \hbar, m_e, e および \epsilon_0 は換算プランク定数, 電子質量 (換算質量), 素電荷, そして真空の誘電率です. 解くべき従属変数 \psi(\mathbf{r}) は波動関数です. つまり, ノルムが である複素スカラー場です. |\psi(\mathbf{r})|^2 は, \mathbf{r} で電子が見つかる確率を示します. 左側の演算子 \hat{H} はハミルトニアンであり, 基本的にシステムの総エネルギーに対応します. ラプラシアンは電子の運動エネルギーを与えますが, ポテンシャル エネルギーは原点にある正に荷電した原子核 (この場合は単一の陽子) によるクーロンポテンシャルによって単純に与えられます. TISE は, 未知の総エネルギー E の固有値問題の形式であり, 変数の分離と級数展開という通常のツールによって正確に解くことができます. 結果として得られる固有状態は, 3つの整数, つまり量子数 n, l, および m によってラベル付けされます. ここで, n,l\in \mathbb{N}, l \leq n および m=-l, \cdots, 0,\cdots,l. \theta と \phi はそれぞれ極角と方位角を示す球面極座標を示し (COMSOL® で使用される定義と同じ), 次のように表現できます.
ここで, R_{nl} は動径波動関数, Y_l^m(\theta, \phi) \propto P_l^m(\cos\ theta) e^{im\phi} は, ルジャンドル多項式 P_l^m(\cos\theta) で表され, 球面調和関数として知られています. 固有エネルギーは主量子数, n にのみ依存します.
ここで, R_H\about13.6057\,\mathrm{eV} はリュードベリ定数として知られています. 最初のいくつかの固有状態の明示的な式を以下の表に示します.
| Eigenstate | R_{nl}(r) | Y_l^m(\theta, \phi) |
|---|---|---|
| \psi_{100} | \frac{2}{a_0^{3/2}}e^{-\frac{r}{a_0}} | \frac{1}{2\sqrt{\pi}} |
| \psi_{200} | \frac{1}{2\sqrt{2}a_0^{3/2}}\left[ 2-\frac{r}{a_0}\right]e^{-\frac{r}{2a_0}} | \frac{1}{2\sqrt{\pi}} |
| \psi_{210} | \frac{1}{2\sqrt{6}a_0^{3/2}}\frac{r}{a_0}e^{-\frac{r}{2a_0}} | \frac{\sqrt{3}}{2\sqrt{\pi}}\cos\theta |
| \psi_{21\pm1} | \frac{1}{2\sqrt{6}a_0^{3/2}}\frac{r}{a_0}e^{-\frac{r}{2a_0}} | \pm\frac{\sqrt{3}}{2\sqrt{2\pi}}\sin\theta e^{\pm i\phi} |
ここでは, 便利な長さのスケールとしてボーア半径 a_0 \equiv \frac{\hbar^2}{m_ee^2}\about 52.9\,\mathrm{pm} を使用しました. 上の表から, より高い主量子数では, 同じエネルギーを持つ複数の状態が存在することがわかります. この縮退は, ポテンシャルの対称性の高い形式から生じます.
水素を超えて進むと, 事態は大幅に複雑になります. 正確な結果は存在せず, 摂動計算は非常に面倒になるため, 数値計算が最も現実的な方法です. 原子および分子構造の従来の数値研究は,
電子のフェルミオン的な性質を扱う方法と組み合わせた, 例えば, Hartree–Fock 法 のような 変分法に基づいています. 固有状態を展開するために一連の基底関数を選択し, 展開係数にわたるエネルギーを最小化する必要があります.
COMSOL Multiphysics® の水素原子
水素原子の場合, TISE は単に 3D の複素数値スカラー場の PDE であるため, 固有値問題の FEM ベースの解決策が可能になります. COMSOL Multiphysics® のアドオンである 半導体モジュール は, シュレーディンガー方程式 インターフェース (別名: schr(以下の表に示すとおり))を含み, 水素原子モデルの構築に使用できます. 必要な設定は非常に簡単です.
半径 A_0\equiv 15a_0 の球を設定し, シュレーディンガー方程式 インターフェースでデフォルトのノード (有効質量と電子のポテンシャルエネルギー) を使用して, 有効質量が m_e に等しくなるようにします (このモデルには周期格子がありません). そして電子のポテンシャルエネルギーは原子核のクーロンポテンシャルに等しくなります. ここで必要な境界条件は, r\rightarrow \infty のときに \psi \rightarrow 0 になることだけです. すなわち, 基底状態を求めているので, 球を薄い層で囲み, 無限要素領域として定義します. 計算速度を向上させるために, 半径方向に徐々に粗くなるメッシュを使用します. 最後に, エネルギースケールを eV として指定し, 固有値検索の開始点として -15 eV を推定します.
下の表は, 最初の2つの主量子数について得られた固有エネルギーとその理論値を示しています.
| n | Analytical Method (-R_H/n^2 (\mathrm{eV})) |
COMSOL® (E_n(\mathrm{eV}) from schr) |
|---|---|---|
| 1 | -13.6057 | -13.6108 |
| 2 | -3.4014 | -3.4013 |
固有値は使用するメッシュに依存するため, 信頼できる結果を得るためにメッシュ細分化スタディを実行することを常にお勧めします. 固有状態または軌道の形状を把握するために, 以下の図に示す 3D 等値面プロットを使用して固有状態をプロットします.

一連の変位した 3D 等値面プロットを使用して可視化した, 摂動のない水素の軌道形状.
原子物理学で広く使用されているラベル付け, 1\mathrm{s}, 2\mathrm{s}, 2\mathrm{p}_x,\cdots を採用します. s 状態は放射対称であるのに対し, 各 p 状態は 3 つの相互に垂直な軸の 1 つに沿って円筒対称であることがわかります. 波動関数が球対称である s 状態の場合, 動径確率密度は次のように定義される単純な解析形式になります.
解析結果とシミュレーション結果の比較を以下に示します.
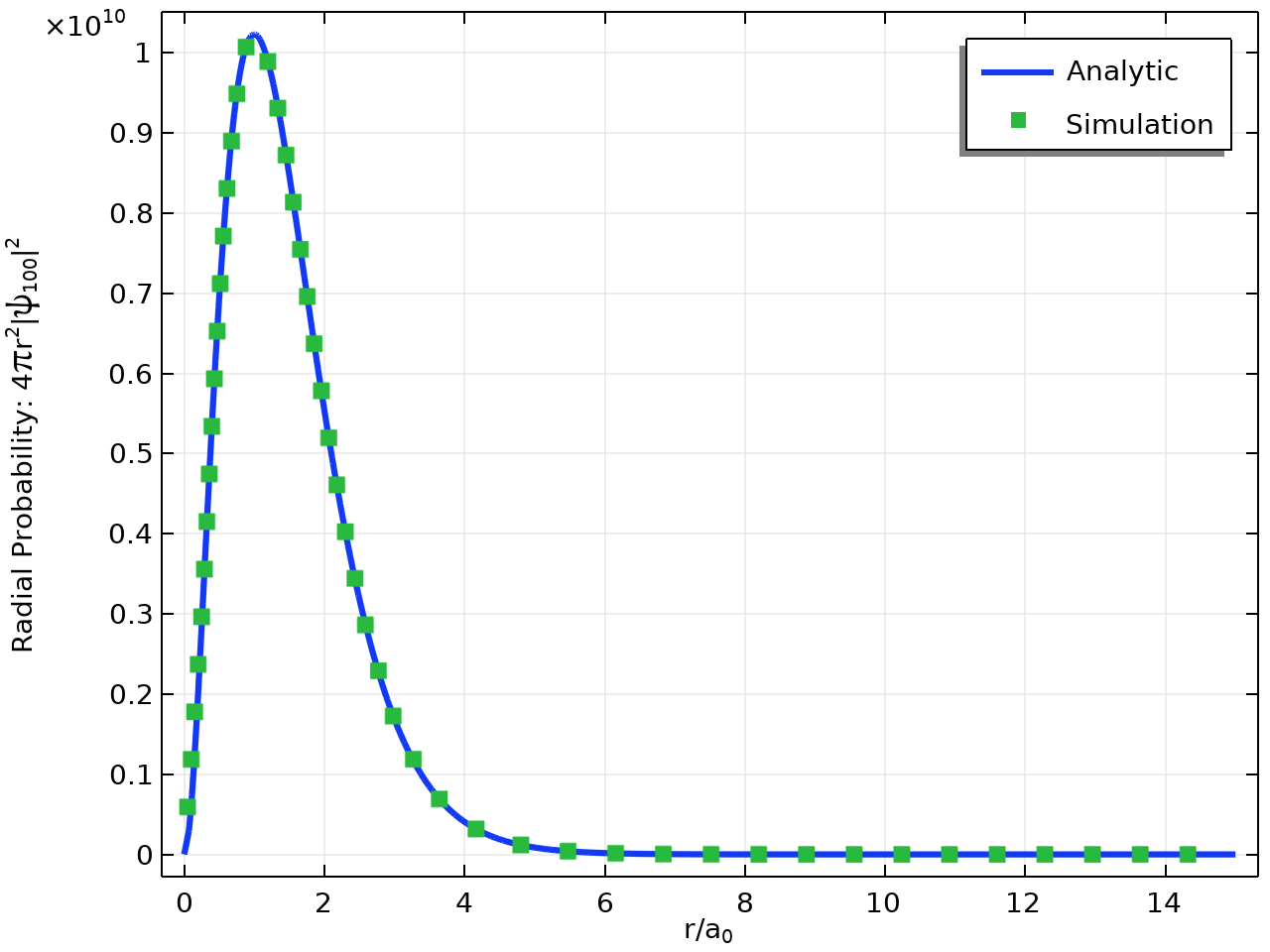
1\mathrm{s} 状態 (基底状態) の動径確率: 厳密解 (線) と, COMSOL® を使用して得られた数値結果 (点) .
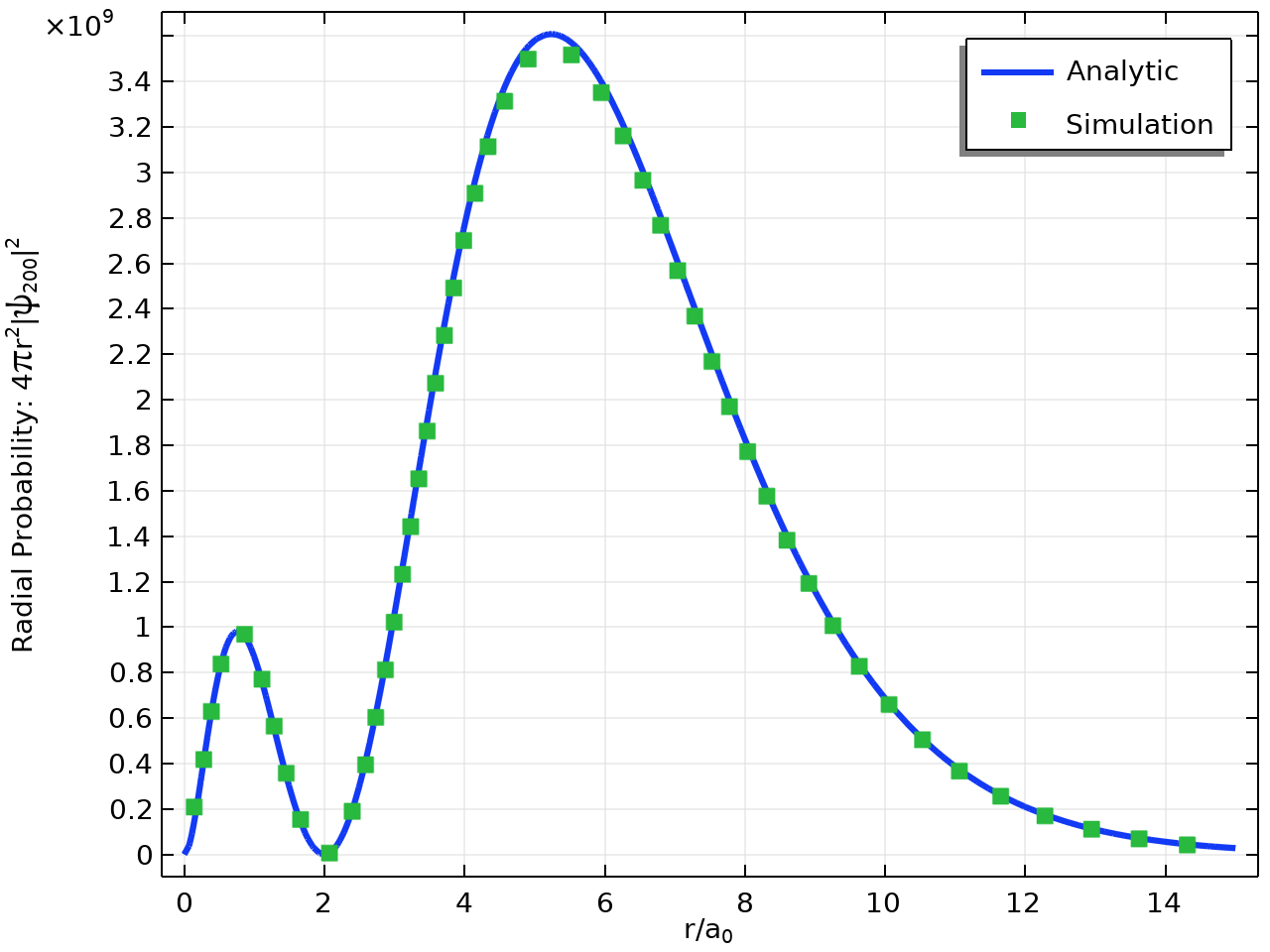
2\mathrm{s} 状態 (第一励起状態) の動径確率: 厳密解 (線) と, COMSOL® を使用して得られた数値結果 (点).
シュタルク効果
たとえばz 軸に沿った外部電場は, 以前に説明した縮退の一部を解除します. 次の項をハミルトニアンに追加する必要があります.
結果として生じる TISE はもはや正確に解くことができないため, 摂動理論に頼らなければなりません. 一次近似で, 1\mathrm{s}, 2\mathrm{p}_x, および 2\mathrm{p}_y 状態はエネルギー (または形状) が変化しません. ただし, 外部場は 2\mathrm{s} 状態と 2\mathrm{p}_z 状態の間の混合を引き起こし, その結果, 2つの準位に分かれます. これはシュタルク効果の一例であり, 実験的な検査測定によって観察できます. エネルギー準位の補正は次のように計算できます.
一方, COMSOL® を使用してシュタルク分割を数値的に見つけることは, 外部場がない場合と同じくらい簡単です. 別の電子ポテンシャルエネルギーノードをモデルに追加するだけで, 次のようになります. 分割されたエネルギー準位と対応する軌道形状を容易に取得できます. 効果をはっきりと見えるようにするために, \sim2\times10^{8}\mathrm{V/m} という非常に高い外部場を使用しました.
| 分割エネルギー準位 | 摂動理論 (eV) | COMSOL® (eV) |
|---|---|---|
| E_2+\Delta E_{\mathrm{Stark}} | -3.3714 | -3.3715 |
| E_2-\Delta E_{\mathrm{Stark}} | -3.4314 | -3.4315 |
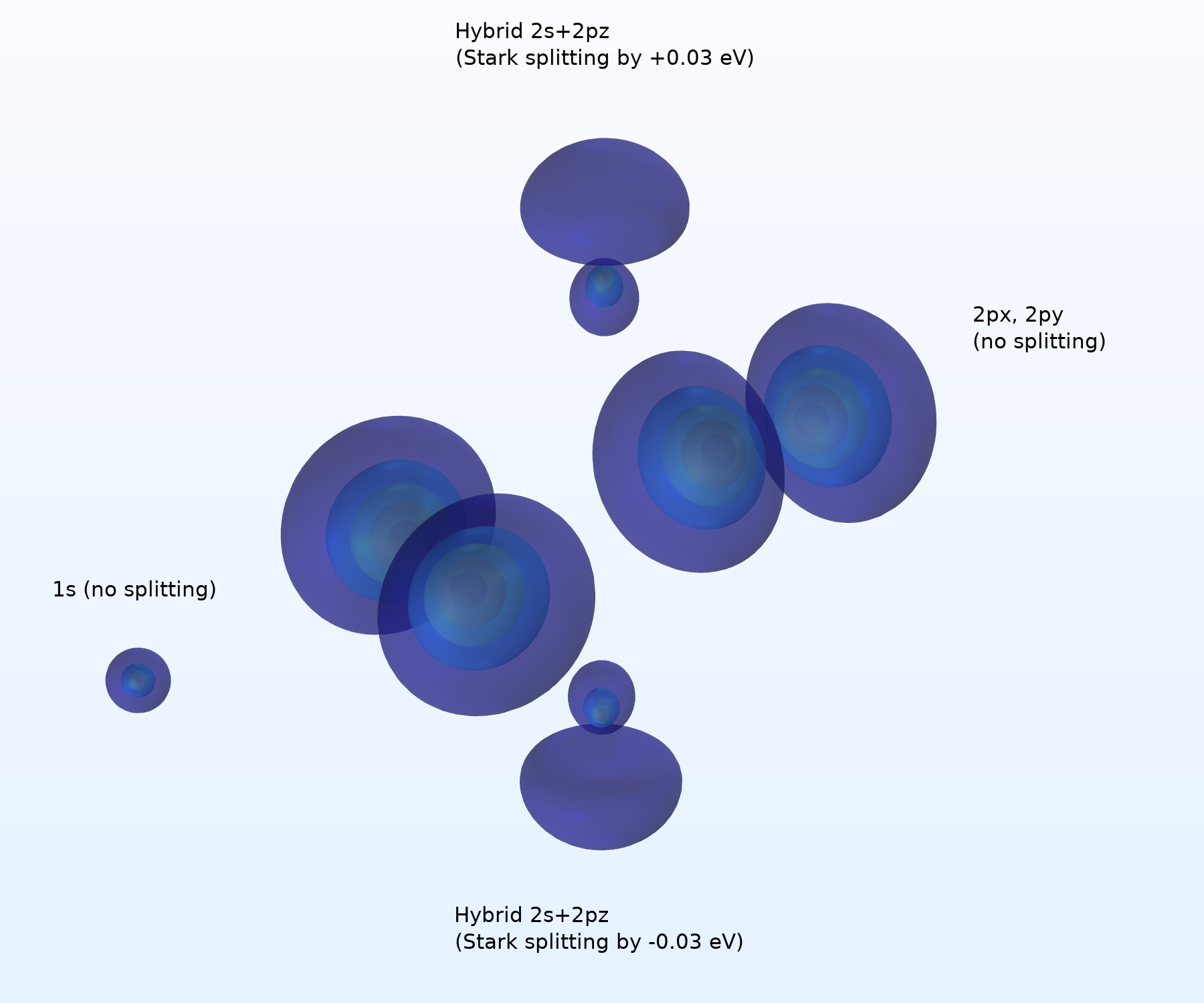
z 軸に沿った外部電界が存在する場合の軌道形状
まとめ
このブログでは, 水素原子を通して量子力学の基礎をいくつか説明し, COMSOL Multiphysics® のシュレーディンガー方程式 インターフェースを使用して結果を再現する方法を説明しました. ただし, ここで紹介したモデルは単に教育学的に興味深いものではありません. ソフトウェアの機能の有用な検証例として機能し, ドーパント状態が水素のような波動関数を使用してモデル化されることが多い半導体物理学に直接関連しています. このモデルとブログは, COMSOL® でより正確な量子力学的シミュレーションを作成するためのリファレンスとして使用できます.
水素原子をさらに詳しく調べることに興味がある場合は, 以下のボタンをクリックして, ここで説明されているサンプルモデルをダウンロードしてください:
その他の参考文献
量子力学についてもっと知る:



コメント (0)