ボーズ・アインシュタイン凝縮体における渦格子形成モデル

ボーズ・アインシュタイン凝縮は, 光子やヘリウム 4 などの巨視的数のボーズ粒子が同じ量子状態を占める量子力学的現象であり, 超流動, 超伝導, レーザーなどの効果をもたらします. 最近では, 閉じ込められた希薄冷却原子で実現されています. このような系が全体として回転するのではなく, 回転摂動を受けると, 渦格子が形成されます. ここでは, 渦格子形成の魅力的なプロセスをシミュレートするためのモデルを紹介します. このモデルは, COMSOL Multiphysics^® ソフトウェアのバージョン 5.6 以降で使用できます.

シュレディンガー方程式フィジックスインターフェース

シュレーディンガー方程式フィジックスインターフェースは, COMSOL Multiphysics^® のアドオンである半導体モジュールで使用できます. 最も単純な使用例では, ポテンシャルエネルギーランドスケープの影響下にある非相対論的粒子のダイナミクスを記述します. (文献 1) エンベロープ関数近似を使用すると, 量子井戸, ワイヤー, ドットなどの量子閉じ込め固体系をモデル化するために使用できます. (文献. 2) Gross-Pitaevskii 方程式の形にキャストすると (文献. 3 および 4), このブログ投稿で示すように, ボーズ凝縮システムをシミュレートするためにも使用できます.

渦格子形成実験

Madison, Chevy, Bretin, Dalibardは 2001 年に実験研究を発表し (文献 5), 回転するレーザー場によって撹拌されたボーズ・アインシュタイン凝縮原子の閉じ込められた雲内での渦格子の核生成と形成を鮮明に示す一連の印象的な画像 (論文の図 3) を示しました. 同じ図で, 彼らは楕円率 |\tilde\alpha| の時間発展もプロットしました (以下の 式 (7) を参照). これは, 系が動的不安定性の期間を経て渦格子の低エネルギー状態に落ち着くときに, 最初の振動に続いて |\tilde\alpha| がほぼゼロに崩壊することを示しました.

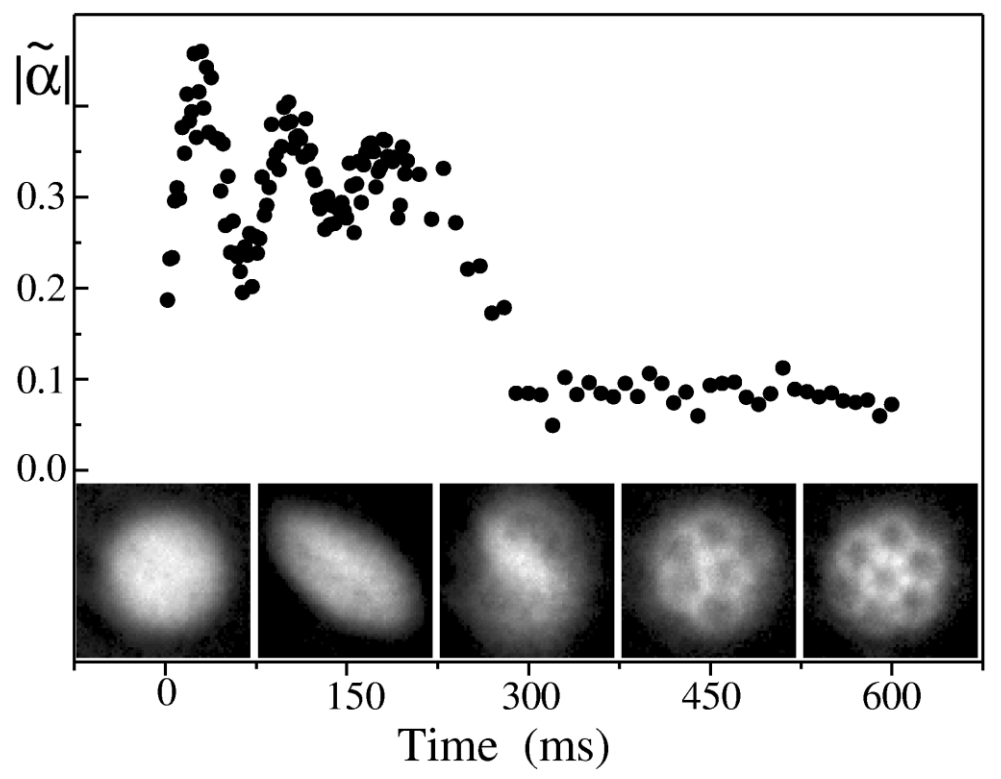
図3はMadisonらによる実験論文より（文献 5）.

主なトラッピングポテンシャルは, 横方向および縦方向のトラッピング周波数 \omega_t と \omega_z によって特徴付けられます:

ここで, m は原子質量です.

トラッピング周波数の比 \lambda\equiv\omega_t/\omega_z は, 文献 1 の図3のキャプションに示される通り, 9.2です.

回転レーザー場からの光ポテンシャルは次のように近似できます.

(2)

ここで, X および Y 軸は周波数 \Omega で, z 軸周りを回転します.

総ポテンシャル V_{trap}+V_{laser} は, トラッピング周波数 \omega_{X,Y}^2\equiv\omega_t^2(1+\epsilon_{X,Y}) と \omega_z によって特徴付けられます.

レーザーを調整することで, 次のように定義されるアスペクト比\epsilonの異なる値を生成することができます.

(3)

特性周波数パラメーター \bar\omegaは, 回転周波数 \Omega: \Omega\equiv\tilde\Omega \bar\omegaの参照として次のように定義されます.

(4)

たとえば, 文献 1 の図 3 は, \tilde\Omega = 0.7 で作成されています. さらに, \bar\omega は, 楕円率 |\tilde\alpha| を定量化するためにも使用されます. これについては, 後ほど詳しく説明します. ただし, この実験は, アスペクト比 \epsilon が時間経過とともに増減する状態で実行されました. したがって, 定義 (4) が \epsilon_X と \epsilon_Y の任意の組み合わせに使用される場合, \bar\omega の値も時間経過とともに増減します.

回転周波数 \Omega と楕円率 |\tilde\alpha| の確実な基準として \bar\omega の定数値を維持するために, モデルで \bar\omega を評価するときに, \epsilon_X と \epsilon_Y に定数値 0.03 と 0.09 を使用します. 基準値 0.03 と 0.09 は, 文献. 2 で引用されている同じグループによる以前の実験論文に基づいています.

最後に, 楕円率|\tilde\alpha|は次のように定義されます. トラップされた凝縮体の密度プロファイルは, Thomas–Fermiプロファイルによってよく近似されます:

(5)

ここで, \mu_{TF} が化学ポテンシャル (Thomas–Fermi 近似の範囲で), g=4\pi\hbar^2a/m は散乱長 a (|F=2, mF=2> 基底状態の⁸⁷Rb で=5.5 nm) で設定される結合定数です.

パラメーター\alphaは, 上記の式(5)で与えられる密度プロファイルの横方向のサイズ(R_XとR_Y)によって定義されます:

(6)

楕円度パラメーター\tilde\alphaは次のように定義されます.

(7)

理論

このモデルでは, Tsubota ら (文献 2) の理論的アプローチに従い, 回転座標系で Gross-Pitaevskii 方程式を現象論的減衰とともに解くことで, この壮大な時間発展プロセスをシミュレートします (文献 3):

(8)

ここで \gamma は減衰係数, \mu は凝縮原子数を常に保存するために調整するための化学ポテンシャルパラメーター, -\Omega L_z=i\hbar\Omega(x\partial_y-y\partial_x) は回転座標系での遠心力項です.

Choiら（文献 3）は, 減衰係数\gammaを推定する式を示しました:

(9)

ここで, K_1 は修正ベッセル関数であり, 凝縮体とその周囲の熱原子の間に平衡があると仮定しています.

Thomas–Fermi 近似は, 減衰係数\gammaなどの多くの重要なパラメーターの良好な推定値を提供します. 円筒対称トラップのピーク密度とサイズパラメーターは, 以下のようにまとめられています:

(10)

ここで, N は凝縮体の原子数です.

渦格子形成のモデリング

モデルパラメーター

Gross-Pitaevskii 方程式 (8) は, 半導体モジュール の シュレーディンガー方程式 フィジックスインターフェースを使用して簡単に実装できます. モデルを構築する際, モデルパラメーターを 文献 1 の実際の実験条件と一致させることに特に注意を払ったため, シミュレートされた時間変化は公開されたデータとよく一致しました.

Bretin の論文によると, 撹拌レーザーは瞬時にオンにされ, その後アスペクト比 \epsilon は 20 ms で上昇し, その後 300 ms 一定に保たれます. したがって, モデルでは, 撹拌レーザー場を常にオンにし, アスペクト比 \epsilon を時間依存にします. 時間依存スタディと定常スタディで同じ式を共有するには, 時間依存スタディの組み込み時間パラメーターと同じ名前 t を使用して時間パラメーターを定義します. 20 ms のランプ持続時間と 300 ms のオフ時間は, それぞれパラメーター tau と t_off として定義されます. 次に, 同じ 20 ms のランプダウン期間を想定して, アスペクト比 \epsilon を上昇および下降させるステップ関数を定義します.

epst=0.032*step1((t+tau)/tau)*(1-step1((t-t_off)/tau))

ランプアップが -20 ms で始まり, t = 0 の時点で終了するように設定されています. \epsilon の大きさは 0.032 に設定されています. これは, 文献 1 と Bretin の論文の両方のテキストに基づいています.

論文からは, レーザー場の長半径と短半径がアスペクト比 \epsilon によってどのように変化するかは明らかではありません. しかし, ランピングの間, 楕円の面積は一定であると仮定するのが妥当と思われます. したがって, 攪拌レーザー場からの光学ポテンシャルの \epsilon_X および \epsilon_Y パラメーターについて, 次の式が得られます:

epsX=(epst+sqrt(0.03*0.09+epst^2-0.03*0.09*epst^2))/(1-epst),

epsY=(-epst+sqrt(0.03*0.09+epst^2-0.03*0.09*epst^2))/(1+epst).

これらのアスペクト比パラメーターが準備できたら, 実験セクションで説明されているようにトラッピングパラメーターを入力します. 凝縮体の原子数は 1.5e5 に選択されます. これは実験の範囲と一致し, 実験の渦の数に最もよく適合します. 減衰係数 \gamma を推定するために, 文献 1 に基づいて 100 nK の温度が使用されます.

3D 凝縮体を近似するために 2D モデルを使用するので, Thomas–Fermiの式 (10) を使用して, 妥当な面外厚さを計算します. 2D モデルのピーク密度が 3D のThomas–Fermiのピーク密度と一致するように面外厚さの基準を選択すると, 面外厚さ L の次の式が得られます:

(11)

初期定常条件

まず, 関連するモデル例 Bose–Einstein 凝縮の Gross–Pitaevskii 方程式 と同じ方法で, 2 つのスタディを使用して凝縮体の定常状態を解きます. これにより, 後続の過渡スタディの初期条件が生成されます.

(8)の相互作用エネルギー項g|\psi|^2については, 組み込み変数schr.Prを面外厚さLで割って, 3Dの粒子密度を求めます. (schr.Pr の意味は, 通常のシュレディンガー方程式の意味で通常の ”確率密度” とは異なることに注意してください. ここで, 従属変数 \psi はGross–Pitaevskii凝縮秩序パラメータを表し, schr.Pr (\equiv |\psi|^2) は 2D 原子密度を表します. ) 定常スタディにおける波動関数の正規化のためのグローバル方程式 N=\int|\psi|^2 では, 全エネルギーはThomas–Fermi化学ポテンシャル \mu_{TF} によってスケーリングされるため, 解くべきグローバル変数は 1 のオーダーになります.

下の図は, 結果として得られた X 軸上の粒子密度プロファイルを Thomas-Fermi 近似によるものと比較したものです. 予想どおり, 両者はよく一致しています.

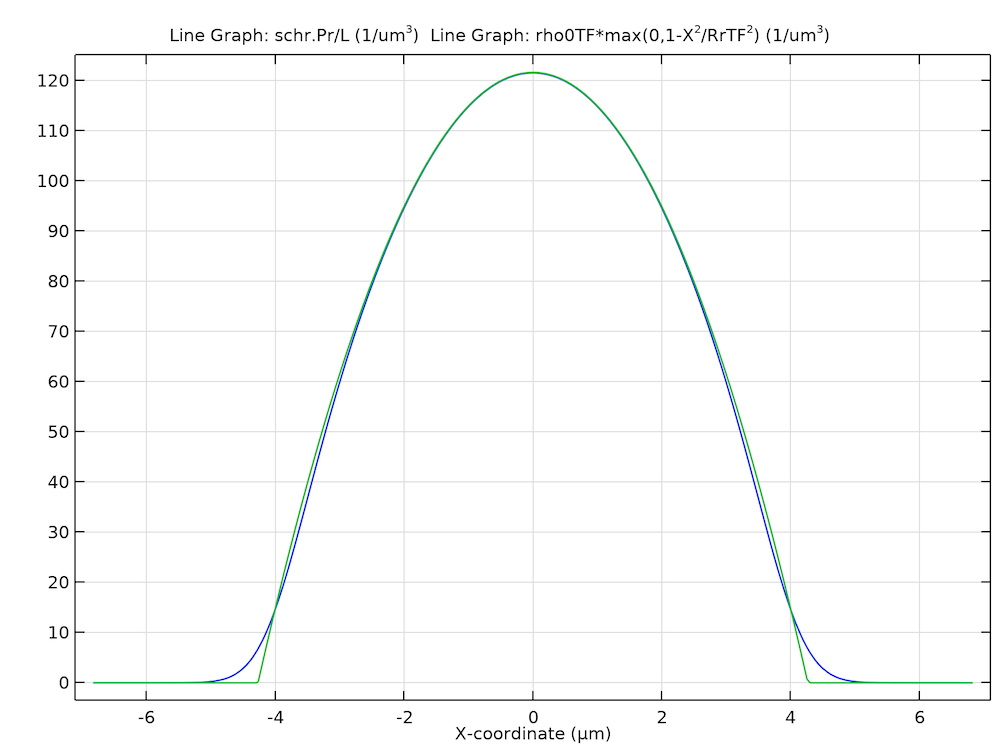
X軸上の粒子密度プロファイルの計算された定常解（青）とThomas-Fermi近似からの定常解（緑）.

回転座標系, 散逸, 正規化

定常解が得られた後, 時間依存スタディのためにさらに多くの物理機能が追加されます. 特に, COMSOL Multiphysics^® バージョン 5.6 で利用可能な 2 つの機能が使用されます. 1 つは, 下のスクリーンショットに示すように, 回転座標系機能です.

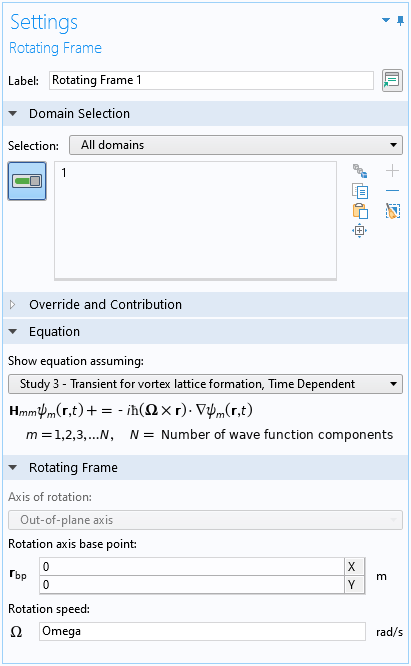
回転座標系機能の設定ウィンドウ.

このような 2D モデルの場合, 回転軸は平面外方向に固定されます. 3D モデルの場合, ユーザーは任意の方向の軸を選択できます.

もう 1 つは, 現象論的減衰のための 散逸 機能です. これは, 系が渦格子の低エネルギー状態に緩和するために重要です. 下のスクリーンショットを参照してください.

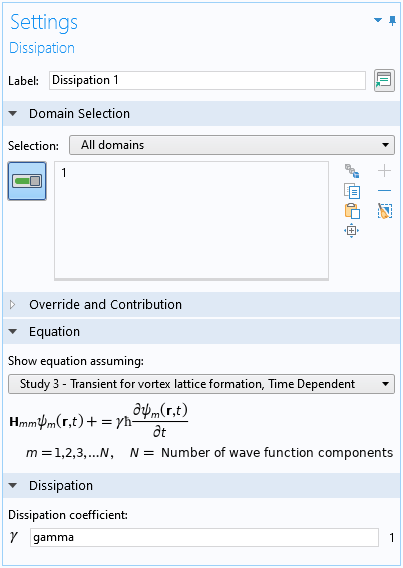
散逸機能の設定ウィンドウ.

文献 2 に従い, 定常スタディと同様に, 化学ポテンシャルを調整することで凝縮体中の原子数を維持するためにグローバル方程式が使用され, 解かれるグローバル変数は, Thomas-Fermi 化学ポテンシャル \mu_{TF} のエネルギースケールで 1 のオーダーにスケーリングされます.

動力学的不安定性

系は, 低エネルギーの渦格子状態に落ち着く前に, 動力学的的不安定性の期間を経ます. この物理プロセスの確率的性質により, 実行ごとにシミュレートされた時間履歴に大きな変化が生じます. 結果として生じる格子内の渦の数も変化する可能性があります. 数値収束を改善するために, ソルバー設定にいくつかの調整が行われます. 初期条件は定常スタディからの物理的解であるため, 整合的初期化の設定を無効にすることができます. これは, エラー制御から代数状態を除外するのに役立つことがよくあります. 多数の反復を伴う自動ニュートン法は, 非線形性が深刻な不安定期間を乗り切るのに役立ちます.

以下のアニメーションは, 計算された粒子密度プロファイルを時間の関数として示しています. 凝縮物の初期の振動/回転期間の後, 渦が周辺に形成され始めます. その後, 渦がランダムに動く動力学的不安定期間が続きます. (この期間中, アニメーションは遅くなります. ) 最終的に, 系は渦格子の低エネルギー状態に落ち着きます. ショーをお楽しみください!

時間の関数として計算された粒子密度プロファイル.

下のグラフはアニメーションのスナップショットのいくつかを示しています.

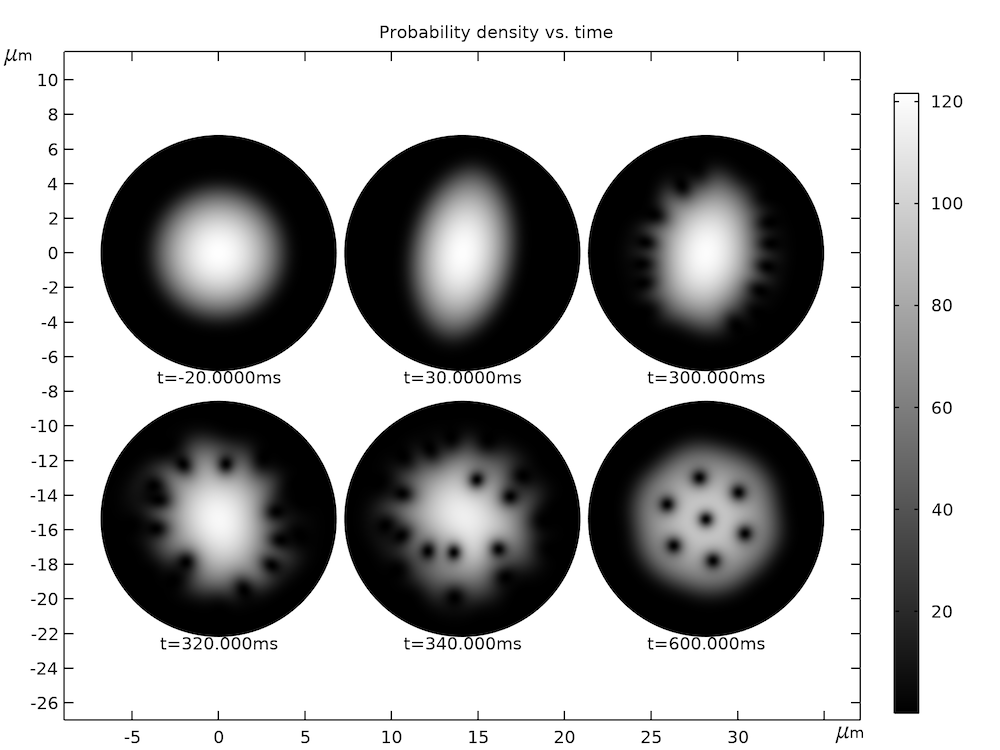
時間の関数として計算された粒子密度プロファイル.

実験セットアップの光学画像システムの実際的な制限により, 原子がまだトラップされている間に, 上のグラフに示されているような密度プロファイルの画像を取得することはできません. 代わりに, 実験では, 原子をトラップから解放し, 雲を 25 ms の間自由に膨張させて, 約 300 um のサイズにします. 雲のアスペクト比も, 自由膨張の前後で劇的に変化します. 最初の葉巻形は, 膨張の前後で長辺と短辺が入れ替わり, 最終的にパンケーキ形になります. シミュレートされたトラップ内密度プロファイルと, 膨張後の原子雲の公開画像を比較する場合は, この点に留意する必要があります.

結果の解析

上のアニメーションとグラフに示されている時間発展のプロセスは, 単一の楕円率パラメーター |\tilde\alpha| に要約できます. これは, 粒子密度プロファイルを単純な関数にフィッティングして楕円の長軸と短軸 R_X と R_Y を抽出し, 次に 式 (7) を適用することによって得られます. 上のグラフに示されているシミュレートされたトラップ内密度プロファイルの場合, Thomas–Fermi 近似は適切なフィッティング関数を提供します. これを各時点の密度プロファイルにフィッティングすることで, 楕円率パラメーター |\tilde\alpha| を時間の関数として計算できます. 下のグラフはその結果を示しています (青い点). |\tilde\alpha| の初期振動と最終的な崩壊の時間スケールは, 文献 1 の図 3 に示されているデータとよく一致しています. 大きさはわずかに異なりますが, これは, 上で説明したように自由膨張の前後で形状が変化する可能性があることを考えると理解できます.

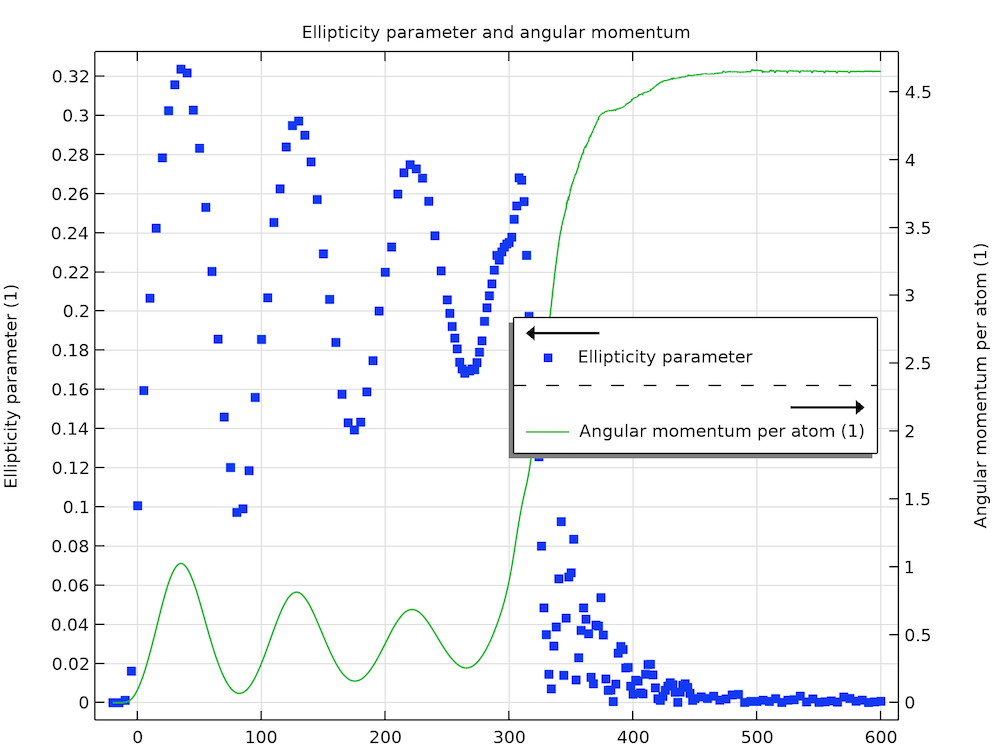
楕円率パラメーターと原子あたりの角運動量（単位は \hbar）.

振動/回転する完全な雲から渦格子への遷移を特徴付けるもう 1 つの重要なパラメータは角運動量で, これも上のグラフにプロットされています (緑の曲線). 初期の振動と, 最終的に渦の数に比例して一定の角運動量を獲得するという一般的な動作は, Tsubota らによるシミュレーション結果と一致しています (文献 2 の図 3). ただし, ここでは, 結果の時間スケールが実験データにかなり近くなっています.

最適化

最適化モジュールは, 粒子密度プロファイルのフィッティングに使用されます. フィッティングの品質を確認するには, 下のグラフに示すように, フィッティング データの等高線 (シミュレートされた密度プロファイル) とフィッティング関数の等高線 (Thomas-Fermi 密度プロファイル) を一緒にプロットして比較します.

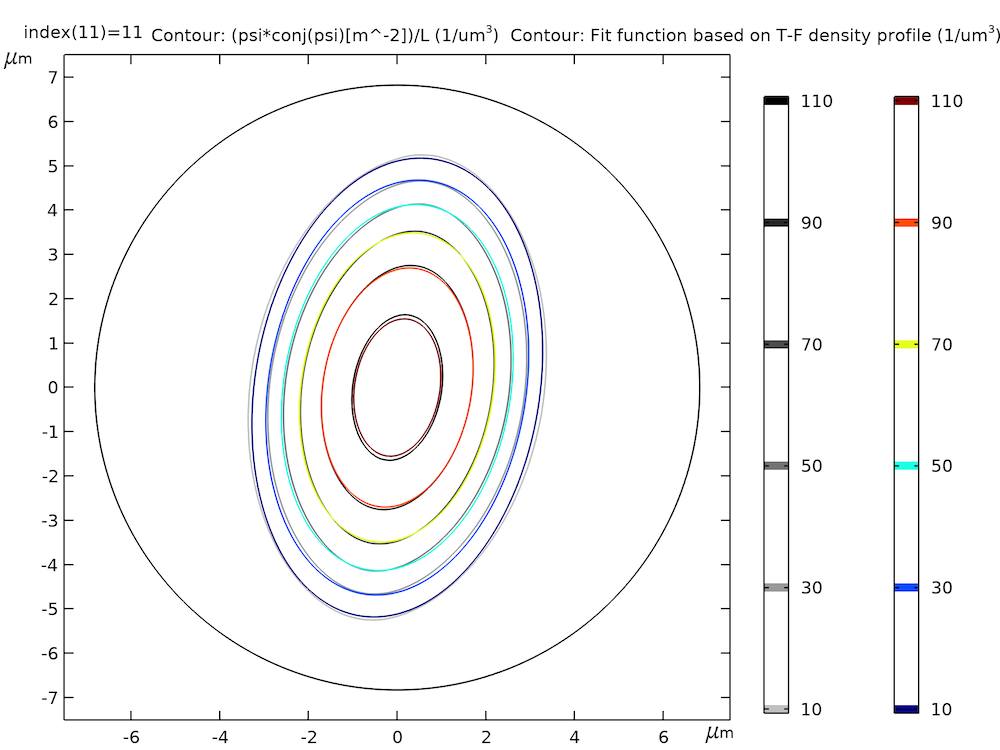
フィットデータ（シミュレートされた密度プロファイル, グレースケール）とフィット関数（Thomas-Fermi密度プロファイル, カラー）.

最適化スキームの設定は, 以下のスクリーンショットに示すように, 適合パラメータの定義から始まります.

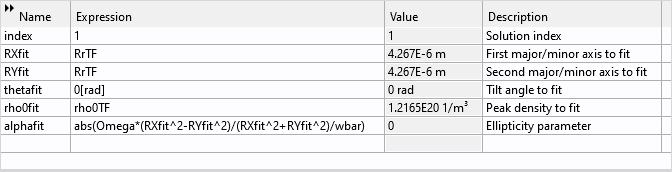
最適化スキームの適合パラメーター.

これらは, 第 1 軸 RXfit, 第 2 軸 RYfit, 傾斜角 thetafit, および適合密度プロファイルのピーク密度 rho0fit です. また, 解参照のインデックスパラメーター index と, 適合パラメーターと 式 (7) を使用して計算された楕円率パラメーター alphafit の適合値も定義されています.

Thomas-Fermi 密度プロファイルに基づく適合関数は, 変数 fit_fn として定義されます. 次に, 計算されたデータと適合関数の差を 2 乗してシミュレーション領域で平均化し, 最適化スタディによって最小化される目的関数として使用します. 目的関数の大きさが大きくなりすぎて最適化で処理できなくなるのを防ぐため, 結果の目的関数が 1 のオーダーに近くなるように, 差を Thomas-Fermi ピーク密度 (式 (10) の \rho_0) でスケーリングします. これは, 下のスクリーンショットで変数 q0 として定義されています.

最適化スタディによって最小化される密度プロファイルと目的に適合する.

次に, 目的関数 q0 と 4 つのフィッティングパラメーターを最適化スタディ設定で使用します. フィッティングパラメーターにはそれぞれ, Thomas-Fermi 近似値を使用して適切な初期値, スケール, 境界が与えられます. 下のスクリーンショットを参照してください.

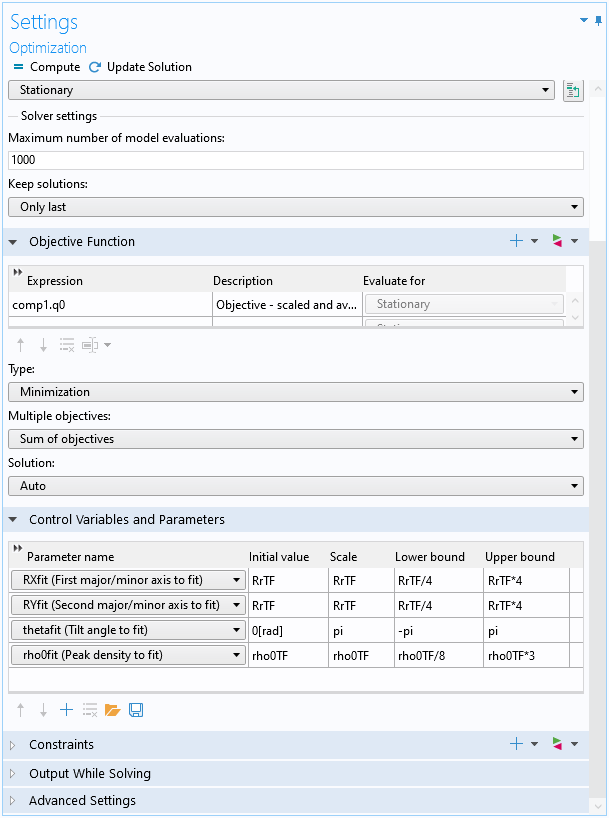
最適化スタディ設定.

各時点の解は, 最初にパラメーター index を使用してパラメトリックスイープを設定することによってフィッティング用に選択され, 次にダミーの定常スタディステップで, 非求解変数の値 セクションが, index パラメーターを使用して各時間ステップで時間依存解を選択するように設定されます. 以下のスクリーンショットを参照してください.

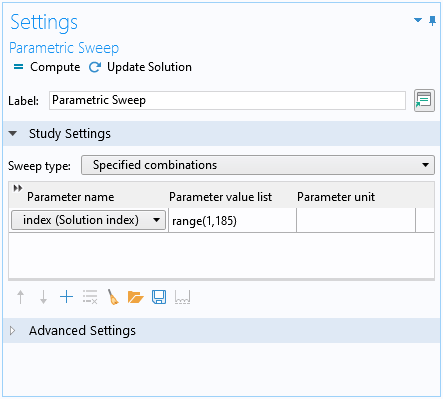
パラメーター index を使用したパラメトリックスイープ.

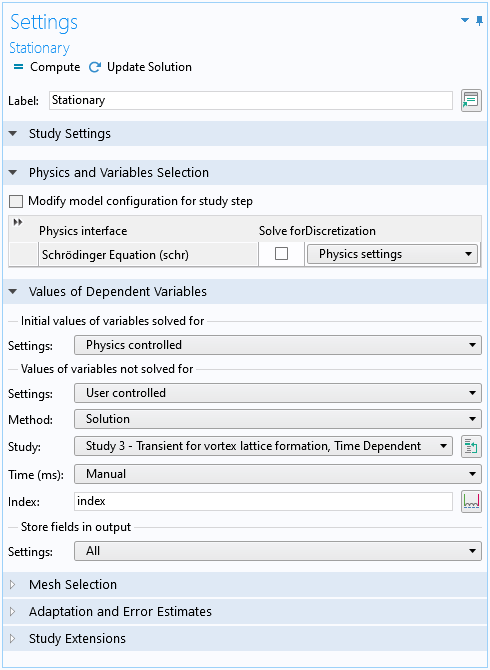
非求解変数の値のセクションを含むダミーの定常スタディステップでは, index パラメーターを使用して各時間ステップで時間依存解を選択するように設定されています.

おわりに

閉じ込められた冷たい原子によって形成されたボーズ・アインシュタイン凝縮体内の渦格子形成の動的プロセスのモデルを使用して, シュレーディンガー方程式フィジックスインターフェースを実証しました. このフィジックスインターフェースを他の興味深い現象にどのように使用したかを, 以下のコメント欄でぜひお聞かせください.

自分で試す

下のボタンをクリックして, 回転するボーズ・アインシュタイン凝縮体の渦格子形成をモデル化してみてください. アプリケーションギャラリに移動し, MPH ファイルをダウンロードできます.

参考文献

1. L. I. Schiff, Quantum Mechanics, McGraw Hill, ed. 3, 1968.
2. P. Harrison, Quantum Wells, Wires and Dots, Wiley, ed. 3, 2009.
3. E.P. Gross, “Structure of a quantized vortex in boson systems”, Il Nuovo Cimento, vol. 20, no. 3, pp. 454–457, 1961.
4. L.P. Pitaevskii, “Vortex lines in an imperfect Bose gas”, Sov. Phys. JETP, vol. 13, no. 2, pp 451–454, 1961.
5. K. W. Madison, F. Chevy, V. Bretin, and J. Dalibard, “Stationary States of a Rotating Bose-Einstein Condensate: Routes to Vortex Nucleation”, Phys. Rev. Lett., 86, 4443, 2001.
6. M. Tsubota, K. Kasamatsu, and M. Ueda, “Vortex lattice formation in a rotating Bose-Einstein condensate”, Phys. Rev., A 65, 023603 (2002).
7. S. Choi, S. A. Morgan, and K. Burnett, “Phenomenological damping in trapped atomic Bose-Einstein condensates”, Phys. Rev., A 57, 4057, 1998.