
COMSOL Multiphysics® ソフトウェアおよびアドオンの音響モジュールでは, 線形化ナビエ・ストークスインターフェースを使用して, 流れと音響の複雑な相互作用の詳細なモデリングが実現されています. バージョン 5.3 のリリースでは, 新しい安定化スキームが追加され, 機能がさらに拡張されました. これにより, 自動車の排気系など, 乱流背景流によって変更されるか, 乱流背景流に依存する音響特性を持つ系の堅牢なシミュレーションが可能になります. ここでは, 重要なモデリングコンセプトを紹介し, アプリケーション例を示します.
航空音響モデリングの概要
定常背景流と音響場の複雑な相互作用は, 音響モジュールの線形化ナビエ・ストークスフィジックスインターフェースを使用してモデリングできます. このインターフェースにより, 乱流と非等温の両方である可能性のある流れが, さまざまな系の音響場にどのように影響するかを詳細に分析できます. これには, 背景流が音響場と相互作用して音響場を変更するすべての線形効果が含まれます. 線形化ナビエ・ストークスインターフェースは, 流れによって引き起こされるノイズ源項を誘発しません. 基本的に, 方程式は, 質量, 運動量, エネルギー保存という CFD の一般方程式に対する完全な線形摂動を解きます.
背景流が音響場に及ぼす影響の詳細をモデル化してシミュレートできることは, 多くの業界やアプリケーション領域で重要です. 自動車業界では, 排気系と吸気系の音響特性は, 流れが通過するときに変化します. たとえば, マフラーの透過損失は, バイパス背景流の大きさに応じて変化します. 航空宇宙アプリケーションでは, 流れが存在するときにライナーと穿孔部が音響的にどのように動作するかの研究は, 非常に興味深いものです. これらのサブ系の詳細な音響特性 (吸収, インピーダンス, 反射係数) は, たとえばジェットエンジンの系レベルの動作に影響します.
マフラーとライナーの例では, 背景流に存在する乱流による音響信号の減衰も, 線形化されたナビエ・ストークス方程式で捉えることができます. さらに, これらのモデルの背景の流れは, 非等温の性質を持つことがよくあります.
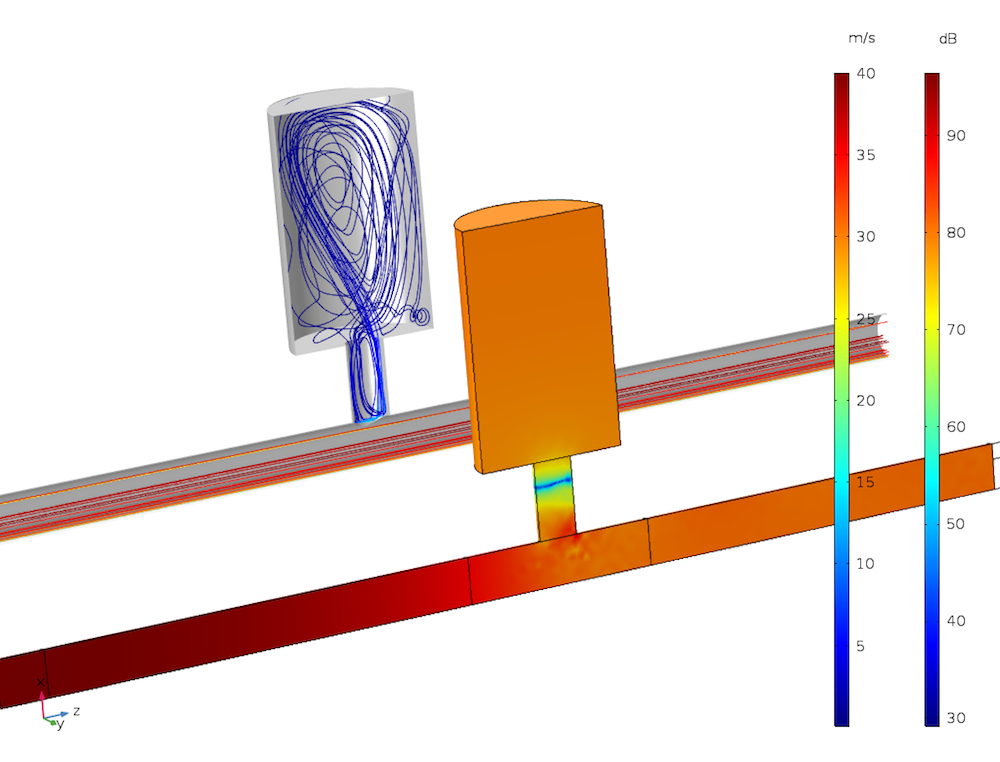
自動車用途の例. 以下に示す流れの例によるヘルムホルツ共振器の結果. 前面のカラーサーフェスプロットは音圧レベルです. 背面の流線は背景の流れです.
線形化ナビエ・ストークスインターフェースには, 構造へのマルチフィジックスカップリングが組み込まれています. これにより, 周波数領域 (または時間領域の線形領域) で流体構造相互作用 (FSI) モデルをすぐに設定できます. 流れ, 音響, 構造振動の相互作用は, 多くのアプリケーションで重要です. 1つのアプリケーション例は, コリオリ流量計の流れ検知です. 一般に, これらのインターフェースは, 背景流れによる流体負荷がかかったときの構造の変化した振動挙動の分析に適しています.
周波数領域での FSI の例: 基本周波数で作動するコリオリ流量計の動き. 表面は構造変形を示しており (位相と振幅は可視化のために大幅に誇張されています), パイプの開いた切り抜き部分はパイプの内面の音圧を示しています.
線形化ナビエ・ストークスインターフェースのその他の用途には, 燃焼不安定性や一般的なダクト内音響の研究, および流れ不安定性の開始の分析や笛吹きが発生しやすい領域の調査などのより学術的な用途があります.
インターフェースには現在, ガラーキン最小二乗法 (GLS) 安定化スキームが含まれており, より堅牢なシミュレーションが可能です. この新しいデフォルト設定により, 支配方程式に含まれる対流項と反応項によってもたらされる数値的および物理的不安定性がより適切に処理されます. さらに, 再定式化された滑り境界条件は, 反復ソルバーを使用してモデルを解くときに適するようになりました. これは, 大規模な産業問題を求解する必要がある場合に重要です.
線形化ナビエ・ストークス方程式
線形化ナビエ・ストークス方程式は, 圧縮性, 粘性, 非等温の流れの支配方程式の完全なセット (ナビエ・ストークス方程式) の線形化を表します. これは, 圧力, 速度, 温度, 密度 (p0, u0, T0, ρ0) によって定義される定常背景流の周りの1次摂動として実行されます. これにより, 従属変数である圧力, 速度, 温度 (p, u, T) の小さな摂動の伝播の支配方程式が得られます. 摂動論では, これらの変数が1次摂動であることを表すために下付き文字 1 が使用されることがあります. 支配方程式 (背景フィールドの下付き文字 0) は次のようになります:
(1)
& \frac{\partial \rho}{\partial t}+\nabla\cdot(\rho_0 \mathbf{u}+\rho \mathbf{u}_0)=M \\
& \rho_0 \left[ \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}\cdot\nabla)\mathbf{u}_0 + (\mathbf{u}_0\cdot\nabla)\mathbf{u} \right] + \rho (\mathbf{u}_0\cdot\nabla)\mathbf{u}_0 = \nabla\cdot\mathbf{\sigma} + \mathbf{F} -\mathbf{u}_0 M \\
& \rho_0 c_p \left[ \frac{\partial T}{\partial t} + \mathbf{u}\cdot\nabla T_0 + \mathbf{u}_0\cdot\nabla T \right] + (\rho c_p)\mathbf{u}_0\cdot\nabla T_0 \\
& \qquad -\alpha_p T_0 \left[ \frac{\partial p}{\partial t} + \mathbf{u}\cdot\nabla p_0 + \mathbf{u}_0\cdot\nabla p \right] -(\alpha_p T)\mathbf{u}_0\cdot \nabla p_0 = \nabla \cdot (\kappa \nabla T) + \Phi + Q
\end{align}
ここで, Φ = ∇u : τ0 + u0 : τ は粘性散逸関数です. M, F, および Q は, 考えられるソースタームを表します. κ は熱伝導係数です (SI 単位: W/m/K). αp は (等圧) 熱膨張係数です (SI 単位: 1/K). βT は等温圧縮率です (SI 単位: 1/Pa). p は定圧における比熱容量 (単位質量あたりの熱容量) です (SI単位: J/kg/K).
周波数領域では, 時間微分は通常どおり, iω との乗算に置き換えられます. 応力テンソルの構成方程式と線形化された状態方程式(密度摂動)は次のように表されます:
(2)
\mathbf{\sigma} & = -p\mathbf{I}+\mathbf{\tau}=-p\mathbf{I}+\mu \left( \nabla \mathbf{u}+(\nabla \mathbf{u})^\textrm{T} \right) + \left( \mu_B -\frac{2}{3}\mu \right)(\nabla\cdot\mathbf{u})\mathbf{I}\\
\rho & = \rho_0 (\beta_T p -\alpha_p T)
\end{align}
ここで, τ は粘性応力テンソル (ストークス式), μ は動粘度 (SI 単位: Pa s), μB は体積粘度 (SI 単位: Pa s) です.
エネルギー方程式ではフーリエ熱伝導の法則が使用されます. 方程式の詳細な導出については, 音響モジュールユーザーガイド を参照してください. 方程式は, 線形化ナビエ・ストークス (過渡) インターフェースまたは 線形化ナビエ・ストークス (周波数領域) インターフェースのいずれかを使用して, 時間領域または周波数領域で解くことができます.
(1)に示された支配方程式を詳しく見ると, そこには異なるタイプの項が含まれていることがわかります:
- 時間依存または周波数依存の項 (方程式の最初の項)
- 拡散項 (粘性および熱伝導による損失)
- 対流項 (u0 ∙ ∇(…) 型)
- 反応項 p ∙ (…), u ∙ (…), または T ∙ (…) 型)
- 考えられるソース項
インターフェースで解かれる方程式の一般的な性質により, 音響 (圧縮性) 波, 渦度波, およびエントロピー波の伝播が自然にモデル化されます. 後者の2つのタイプの波は, 背景流速でのみ対流され, 音速では伝播しません. 音響波が伝播すると, (反応項を介して) 流れと相互作用し, 音響モードから渦度モードとエントロピーモードの両方にエネルギーを転送できます. 支配方程式の反応項は, この流れ音響のような結合の原因です. これは, 渦度波とエントロピー波が背景の流れの解に対する非音響的 (CFD のような) 摂動であるという意味であり, ある程度, CFD と音響の線形相互作用をモデル化します.
多くの航空音響定式化では, 反応項は無視されます. これは, 反応項が ケルビン・ヘルムホルツ不安定性 を生成するプロセスにも関係しているためです. これらは数値的に処理するのが難しい場合があります. 一方, これらの項を無視すると, 音の減衰と増幅の正確なモデリングが失われます. 反応項は, 線形化ナビエ・ストークスインターフェースに完全に含まれています.
COMSOL Multiphysics® では, 不安定性の増加は2つの方法で処理されます. 不安定性の時間的増加は, 時間領域定式ではなく周波数領域定式を選択することで処理できます. 渦度モードが適切に求解されない場合に発生する可能性のある空間的不安定性は, GLS 安定化スキームによって効率的に処理されます.
線形化ナビエ・ストークス方程式でモデル化されたアプリケーションによっては, 音響, 粘性, および熱境界層を求解する必要がある場合があります. これらは, 滑りなしおよび等温境界条件が存在する場合, 振動流の固体表面上に自然に作成されます. 通常, 大規模なモデルでは, 境界層の損失の詳細を含める必要はありません (境界層の厚さと比較した場合). 熱境界層は液体では無視されることも多いですが, 気体では同様に考慮する必要があります. 壁境界条件でスリップまたは断熱オプションのいずれかを選択することで, 2つの効果を無視できます.
背景流と音響の間には, もう1つの間接的な結合が可能であることに留意してください. 音響波が乱流背景流のある領域を伝播すると, 減衰します. この効果は, CFD RANS モデルの乱流粘性を音響モデルに結合することでモデルに含めることができます. この効果は, たとえば, 流れがある状態でマフラー系の透過損失を解析する場合に重要です.
モデリングの考慮事項
計算航空音響学 (CAA) の分野に属する線形化ナビエ・ストークス方程式を解くには, 慎重に検討, 理解, および処理する必要がある数値的課題があります. 前述のように, 支配方程式は物理的 (ケルビン・ヘルムホルツ) および数値的不安定性の両方の影響を受けやすい傾向があります. インターフェースは安定化を使用するため, 残る主な数値的課題は, 背景場変数 (p0, u0, T0, および ρ0) を含む項での数値ノイズの導入を回避することです. これは, 背景流変数の勾配を含む反応項に特に当てはまります.
この問題の可能性は, CFD モデルと音響モデルに異なるメッシュが使用されている場合, および/または背景流と音響の問題に異なる離散化順序が使用されている場合に高まります. 異なるメッシュまたは離散化順序を使用する理由は, 2つの問題で異なる物理スケールと長さスケールを求解する必要があるという事実に起因していることに注意してください. これを防ぐには, CFD から音響への背景流れデータを慎重にマッピングする必要があります. これは, CAA モデリングでよく理解され説明されている手順です. さらに, マッピング手順を使用して CFD データを平滑化できます. これは, 音響モデルにとって詳細が重要でない場合は, 流体力学的境界層などの特定の詳細の全体的な平滑化またはローカル平滑化になります.
COMSOL Multiphysics® では, メッシュ間のマッピングは追加のスタディ手順によって実行されます. この手順の詳細については, 音響モジュールユーザーガイド および線形化ナビエ・ストークスフィジックスインターフェースを使用したチュートリアルモデルで説明されています.
線形化ナビエ・ストークスフィジックスインターフェースを使用してシミュレーションを実行する場合は, 次の点を考慮する必要があります:
- 音響境界層の求解: モデル化された物理的効果とモデルのサイズによって音響境界層を求解する必要があるかどうかを検討します. そうでない場合は, 壁のデフォルトの滑りなしおよび等温条件から滑りおよび断熱オプションに変更します. この選択は, 背景の流れによって求解される詳細によっても動機付けられる場合があります. たとえば, 背景の流れの境界層を完全に求解するには, 通常, 音響で一致する滑りなし条件が必要です.
- メッシュは CFD と音響の両方を求解する必要があります: 重要な幾何学的特徴, 境界層, および勾配の大きい領域は, CFD と音響の両方のシミュレーションに使用されるメッシュによって求解される必要があります. 具体的には, 音響シミュレーションに使用されるメッシュ (CFD メッシュと異なる場合) は, 波長や音響境界層 (モデル化されている場合は上記のポイントを参照) などの音響特徴と, 背景の流れ場の特徴を求解する必要があります.
- マッピング: マッピング手順を使用して, CFD データを音響問題にマッピングします (特に, 異なるメッシュまたは離散化順序を使用する場合). 必要に応じて, 解を平滑化し, 境界層も平滑化します (音響研究でスリップ条件が使用されている場合は, これを行うことができます). 必要に応じて, マッピング手順で背景流れの滑りなし条件を適用します.
- 離散化次数: デフォルトでは, 線形化ナビエ・ストークスインターフェースは従属変数に対してすべて1次離散化を使用します. これは, ほとんどのモデルで適切な選択です. ただし, 滑りなしおよび等温条件が使用されている場合は, 速度および温度変数に対して2次離散化に切り替えると有利になる場合があります. これにより, 壁付近の空間解像度が向上しますが, 解く自由度も増加します.
流れのあるヘルムホルツ共振器
ヘルムホルツ共振器 (排気系で使用) は, 狭く特定の周波数帯域を減衰します. 系内に流れが存在すると, 共振器の音響特性とサブ系の透過損失が変化します. ヘルムホルツ共鳴器チュートリアルモデル は, 平均流が存在する場合のメインダクト (共鳴器は側枝として配置) の透過損失を調べます.
平均流を計算するには, マッハ数 Ma = 0.05 および Ma = 0.1 の SST 乱流モデルを使用します. 線形化ナビエ・ストークス (周波数領域) インターフェースを使用して, 音響問題を解きます. 次に, 音響モデルを平均流速, 圧力, および乱流粘性と結合します. 予測された透過損失は, 公開された文献 (文献 1) の結果とよく一致しています. 共鳴を正しく配置し, 透過損失の振幅を正しくするには, モデルで対流項と拡散項を適切にバランスさせる必要があります. これはモデルで実現されます.
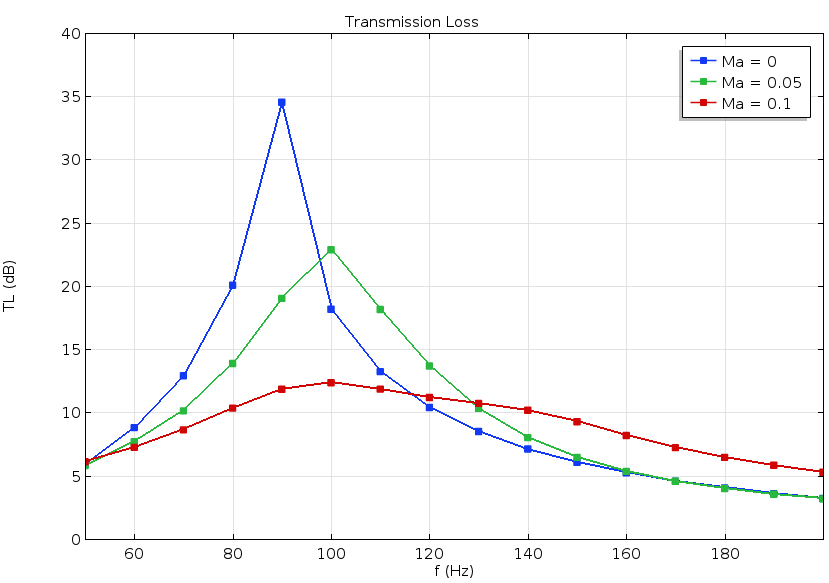
共振器の透過損失は, 背景流の周波数とマッハ数の関数として表されます.
Ma = 0.1 の場合の 100 Hz での系内の圧力分布. 平面波は流れの上流の左側から入射します.
音響ライナーとかすめ背景流
音響ライナーとかすめ背景流のチュートリアルモデル では, 音響ライナーは薄いスリットのある8つの共振器で構成され, 背景かすめ流はマッハ数 0.3 です. ライナー上の音圧レベルが計算され, 公開された研究論文 (文献 2) の結果とよく一致しています. この例では, CFD モジュールの SST 乱流モデルを使用して流れを計算し, 線形化ナビエ・ストークス (周波数領域) インターフェースを使用して音響伝播を計算します. 音響境界層が求解され, 壁付近の空間解像度を向上させるために, デフォルトの1次離散化が2次式に切り替えられます.
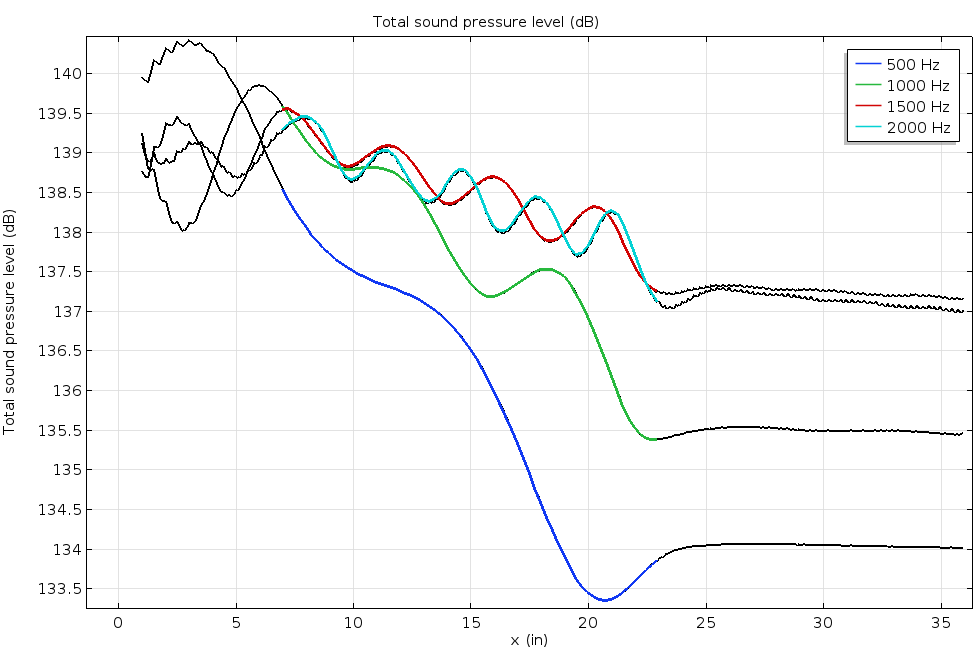
曲線は, 4つの駆動周波数におけるライナー上面の音圧レベルを示しています. 曲線の色付き部分は, ライナーの範囲を示しています. これらの結果は, 参照された研究論文の実験結果とよく一致しています.
平面波がライナー上を伝播する際の音響速度の変動. 最初の4つのライナーを示しています. 駆動周波数は 1000 Hz です. カラープロットは速度振幅を示し, 矢印は速度ベクトルを示しています. ライナーの表面の穴の近くでは, 流体と音響の相互作用によって渦度が生成されます.
コリオリ流量計
コリオリ流量計 (質量流量計または慣性流量計とも呼ばれます) は, 通過する流体の質量流量を測定できます. このデバイスは, 流体の密度, つまり体積流量を計算することもできます. コリオリ流量計チュートリアルモデル では, 曲線形状の一般的なコリオリ流量計をモデル化する方法を示します.
流体が弾性構造 (たとえば, 湾曲したダクト) を通過すると, 振動時に構造の動きと相互作用します. コリオリ効果により, ダクト上の2点の変形に位相差が生じ, これを使用して質量流量を決定できます.
これをモデル化するには, 組み込みのマルチフィジックスカップリングを介して, 線形化ナビエ・ストークス (周波数領域) インターフェースを 固体力学 インターフェースに結合します. 背景平均流については, 乱流, SST インターフェースを使用してシミュレートします. このアプローチを使用すると, FSI を周波数領域で効率的にモデル化できます.
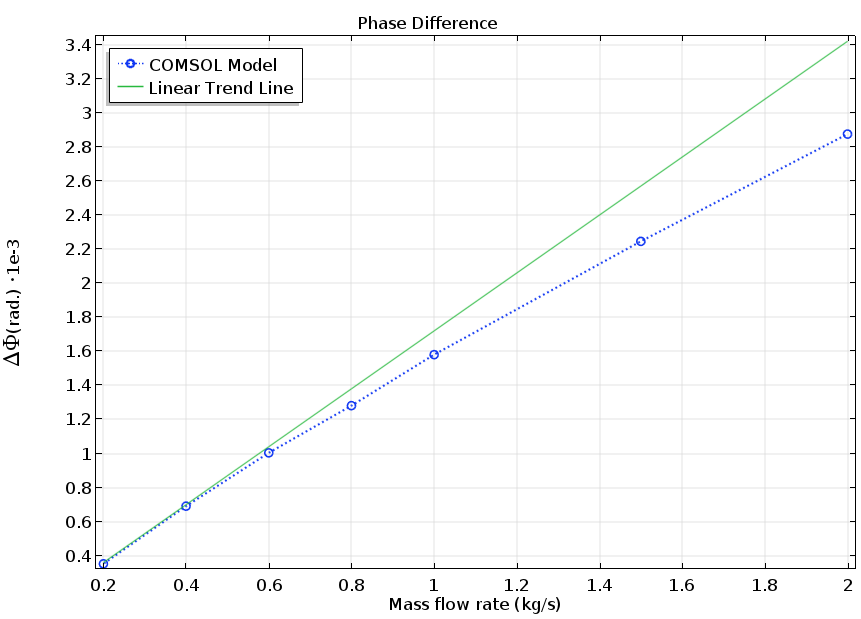
上流点と下流点の位相差 (下のアニメーションの赤い点). この曲線は, コリオリ流量計を実行するために必要な校正結果を表します.
3つの質量流量に対するコリオリ流量計の動き. 流量計は, 構造の固有振動数 fd = 163.5 Hz で作動します. 変形の振幅と位相は, 可視化のために誇張されています. 流量が増加すると, 上流と下流の位相差が増加します.
COMSOL Multiphysics® の CFD および音響シミュレーションの詳細
- アプリケーションギャラリで次の例をご覧ください:
- COMSOL Conference 2016 のプレゼンテーション: “低マッハ数流における円形オリフィスを介した音響散乱” をご覧ください.
- COMSOL ニュース 2017 — 特別版音響 をご覧ください.
参考文献
-
E. Selamet, A. Selamet, A. Iqbal, and H. Kim, “Effect of Flow in Helmholtz Resonator Acoustics: A Three-Dimensional Computational Study vs. Experiments”, SAE International Journal, 2011.
-
C. K. W. Tam, N. N. Pastouchenko, M. G. Jones, and W. R. Watson, “Experimental validation of numerical simulations for an acoustic liner in grazing flow: Self-noise and added drag”, Journal of Sound and Vibration, p. 333, 2014.






コメント (0)