COMSOL® での過渡音圧レベルの計算

過渡音響の問題には, 文献や測定基準で定義されているさまざまな音圧レベルの指標があります. これらの指標は, 過渡音響シミュレーションの結果を騒音計の測定値と比較する場合や, 過渡シミュレーションの結果を対数スケールで解釈しやすくする場合に重要です. これらのさまざまな指標とは何か, いつ使用するか, どのように計算するかを見てみましょう.

音圧レベルの定義

定常高調波騒音の場合, 音圧レベル (\textrm{SPL}) は次のように定義されます:

ここで, p_\textrm{rms} は二乗平均平方根 (RMS) 圧力, p_\textrm{ref} は基準圧力 (例: 空気の場合は 20 \mu \text{Pa}, これも RMS 値) です. 複素振幅 p の高調波励起の場合:

ここで, {}^* は複素共役を表します. したがって, \textrm{SPL} は定常ノイズに対して適切に定義されており, ここで示す式は, COMSOL Multiphysics^® ソフトウェアの圧力音響 (周波数領域) インターフェースを使用して \textrm{SPL} を計算するために使用できます. 結果を簡単に分析できるように, いくつかの変数が組み込まれています.

過渡ノイズの場合, 全時間間隔 (T) にわたる RMS 圧力は次のように計算できます:

この式は区間全体の平均をとるため, 区間内の時間の関数として変化するレベルを比較するのには役立ちません. この目的のために, 追加の指標を分析することができます. このブログでは, 次の点に焦点を当てます:

1. 周波数から時間への FFT スタディのウィンドウ関数機能を使用して, 過渡信号の周波数加重圧力を計算します
2. 時間領域での畳み込みを使用して時間加重音響レベルを計算します
3. パラメトリックスイープを使用して, ユーザー定義の期間にわたって時間平均音響レベルを計算します

周波数重み付け

人間の耳は, すべての周波数の音のレベルを同じように知覚するわけではありません. たとえば, 耳は 1000 \text{Hz} の音に対しては 100 \text{Hz} の音よりもずっと敏感です. 音響測定を分析する際にこの感度を数学的に考慮するために, IEC 61672-1:2013 の一部として A 特性が導入されました. これは, 分析するノイズを調整して周波数を補正する機能です.

他の重み関数:

• C 加重: これは, 高音レベルの周波数依存性の変化など, 耳の非線形応答を捉えることを目的としています.
• Z 加重: これはフラットな応答であり, ゼロ加重を示すために使用されます.

通常の周波数範囲におけるこれら3つの関数 (A, C, Z重み付け) は, 以下のグラフに示されています:

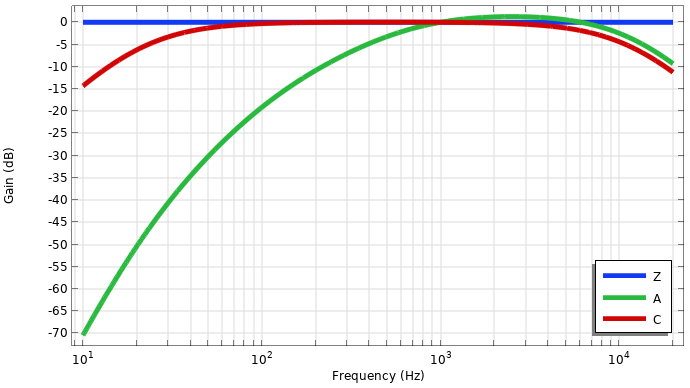
A, C, Z 周波数加重関数のプロット.

重み付け関数の選択は, アプリケーションによって大きく異なります. たとえば, 米国では, 労働安全衛生局 (OSHA) と環境保護庁は, 職業および環境騒音制限に A 加重メトリックを使用しています..

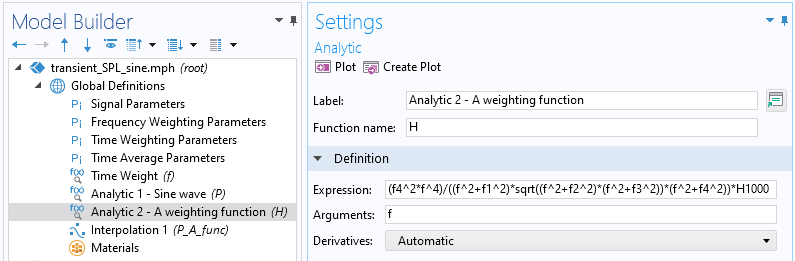
A 加重ゲイン関数は以下の通りです:

ここで, f は周波数で, 定数は f_1=20.6, f_2=107.7, f_3=737.9, f_4=12194 です. 関数は, 1000 \text{Hz} で 0 \text{dB} のゲインを持つように定義されています. 後で, パラメーターと解析関数を使用してこの関数を実装します.

オクターブバンドプロットには, さまざまなタイプの重み付けが組み込まれていることに注意してください. このプロットは, すべての周波数領域データのポスト処理に役立ちます. ヒント: このプロットの包括的な概要については, ブログ “音響シミュレーションのオクターブバンドプロット” をご覧ください.

時間加重音響レベル

時間依存の A 特性音圧 p_A(t) を考えてみましょう. 瞬間音圧レベルは次のように定義できます:

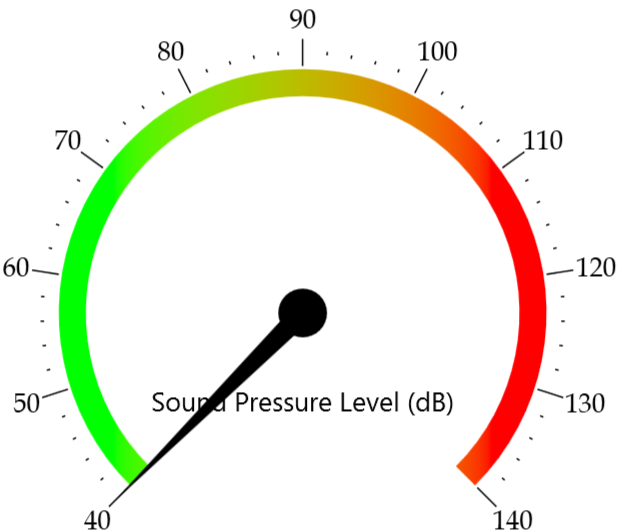
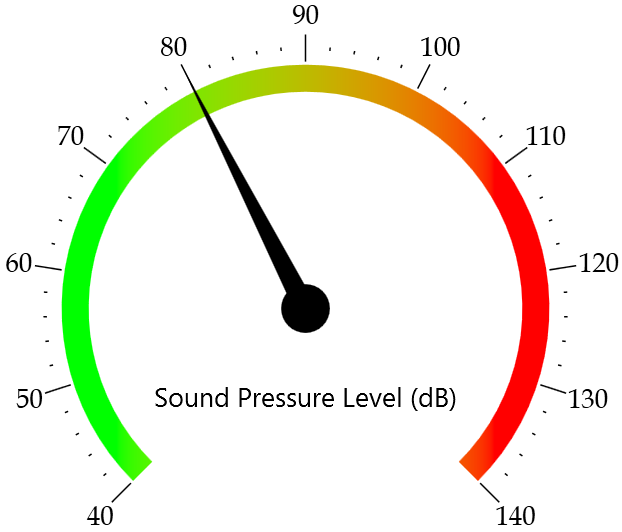
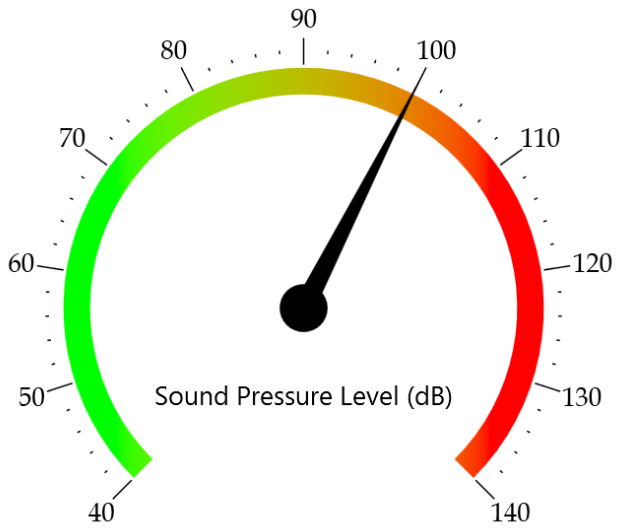
しかし, これにはいくつか問題があります. まず, p_A(t) = 0 の場合, 結果の演算には 0 の対数を取ることが含まれるため, L_{p_A}(t) は未定義です. 2つ目のより実用的な問題は, 騒音計が初めて使用されたときにさかのぼります. 以下の3つの横並びの画像に示すように, 針インジケータが上下に動いて変化する信号を示します. ただし, これを瞬間音圧レベルの定義に関して見ると, 問題があります. 針が前後に非常に速く動くため, オペレーターが特定の瞬間の測定値を確認するのが困難になります. (参照1)

騒音計の針表示器.

これを克服するために, 時間加重騒音レベルの概念が導入されました. 定義は次のとおりです:

この式では, \tau は時間定数, \zeta は積分に使用される中間変数です. パラメーター \tau は, 低速時間加重の場合は1秒, 高速時間加重の場合は0.125秒と定義されています. これらの仕様に従って製造された騒音計では, 低速および高速時間加重を選択できます.

時間加重圧力は以下の通りです:

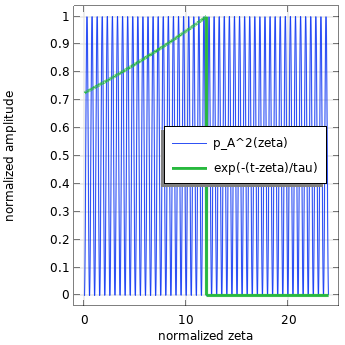
この式を分解してみましょう. 関数は, 圧力関数の二乗と指数関数的減衰関数の畳み込みです. 畳み込みとは, 2つの関数を乗算して積分する数学的な演算です. このプロセスでは, 関数の1つが反転され, 中間軸 (この場合は \zeta) に沿って段階的にシフトされます. t = \frac{6 \pi}{\omega} の瞬間に圧力 p_A(t) = \sin{\omega t} で高速時間重み付けを行うために, \tau = 0.125s を使用するとします. これを可視化するには, 周期 T = \frac{2 \pi}{\omega} で正規化された両方の関数を \zeta 軸上にプロットします.

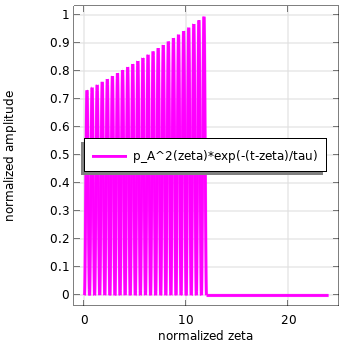
畳み込み積分の個々の関数 (左) と, 畳み込み積分の被積分関数, 離散時間でそれらを掛け合わせた結果 (右).

両方の関数を掛け合わせると, 積分のために残るのは3番目の関数です. これは, 指数関数の現在のタイムスタンプによって重み付けされた時間間隔でのみゼロ以外になります. 時間が経過するにつれて, 指数関数が圧力信号と重なる部分が増えることは明らかであるため, この純粋な正弦波の場合, 積分はある点まで増加すると予想されます.

実際の例に戻ると, 時定数は針の動きを効果的に遅くし, オペレーターが実際に針が変化するのを読み取ることができるようにします. デジタル技術が登場する前は騒音計に使用されていましたが, 時間加重騒音レベルは現在の標準規格や騒音計でも使用されています.

等価連続騒音レベル

IEC 61672-1 では, 時間平均騒音レベル (等価連続騒音レベルとも呼ばれる) も定義されています. 定義は次のとおりです:

平均化期間 T は, 測定を参照して指定する必要がありますが, 任意の期間を表すことができます. 標準では, 騒音計の積分時間として次の時間が推奨されています: T = 10 秒, 1 分, 10 分, 30 分, 1 時間, 8 時間, または 24 時間. この場合, 畳み込みは行われず, これは単に定義された期間の RMS です.

時間平均圧力は以下の通りです:

数秒以下の短い平均化期間の使用は, 短時間等価連続雑音レベル, または短時間 Leq として知られています. これは, 長期間にわたって録音されたサウンドのデータの忠実度をかなり高く維持しながら, データの保存と転送を削減するのに役立ちます.

例 1: 正弦波圧力信号

周波数重み付け

ここでは, 一定振幅および一定周波数の単純な正弦波波形を考慮した検証例を示します. これは, 式 P0*sin(2*pi*fdrive*t) を持つ解析関数を使用して実装できます. パラメーターを使用して, 圧力振幅 1\text{Pa} および駆動周波数 300\text{Hz} を定義します. 最初のステップは, A 重み付け信号を計算することです. 前に定義したパラメーターを使用する A 重み用の2番目の解析関数を追加します.

A 重み付け関数の設定ウィンドウ.

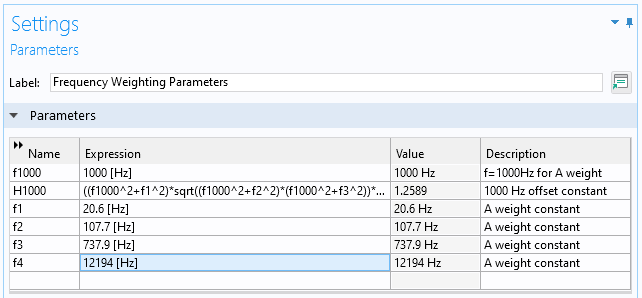
周波数重み付けパラメーターの設定ウィンドウ.

0D コンポーネントを追加し, グローバル ODE および DAE インターフェースでグローバル方程式を使用します.

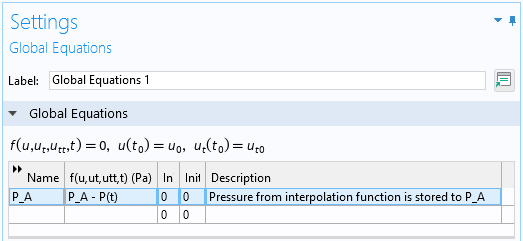
グローバル方程式の設定ウィンドウ.

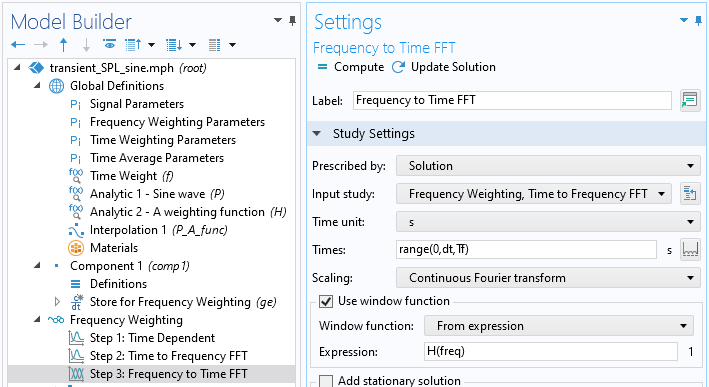
次に, 3つのスタディステップを順番に設定できます. まず, 時間依存スタディを使用して, 上の画像で定義されている方程式を解きます. この方程式は, 信号を従属変数として効果的に保存します. 次に, 時間から周波数 FFT スタディが信号を周波数領域に変換します. 最後のステップ (および周波数重み付けを含むステップ) は, 周波数から時間 FFT スタディステップを使用することです. ここで, ウィンドウ関数の使用チェックボックスをオンにします. ウィンドウ関数では, 式参照を選択し, 前に定義した解析関数の式を挿入します.

周波数から時間 FFT スタディステップの設定ウィンドウ.

いくつかの期間に拡大して解析結果を以下に示します. A 加重圧力は元の信号と同位相ですが, 振幅が減少しています. この振幅の減少は, A 加重周波数ゲイン関数曲線を見ると確認できます. この曲線は, 300 \text{Hz} で約 -7 \text{dB} を示しています. ゲインは, 振幅の対数比, つまり 20 \log_{10} \frac{0.445}{1} = -7.03 を取得することで計算でき, 曲線と一致します.

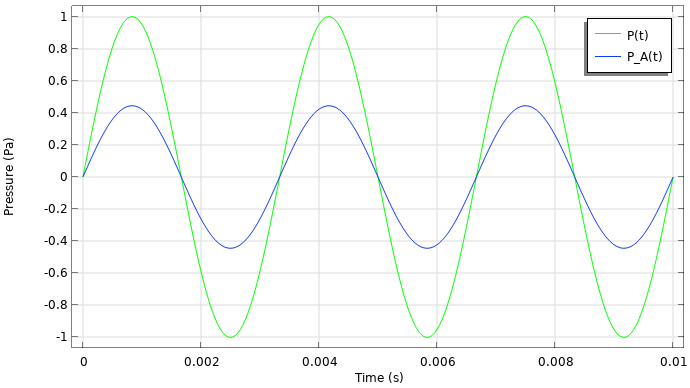
正弦波に周波数加重を使用した後の結果プロット.

時間加重

信号の周波数加重が完了したので, 次に時間加重圧力と時間加重音響レベルを計算します. まず, 新しく計算された P_A(t) の値を, 導出値結果テーブルをデータソースとする補間関数として保存します. これにより, 畳み込みを計算するために必要な P_A(t) の関数が得られます.

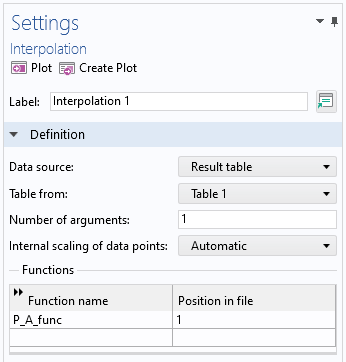
補間関数の設定ウィンドウ.

畳み込みを計算するために, グリッド 1D データセットが追加されます. 使用される式を以下に示します. 式で, \zeta はグリッドによって定義された積分変数座標です. t は指数重み関数のシフトのために導入された新しい変数です. substval() の基本式は integrate(P_A_func(zeta)^2*f(t-zeta),zeta,0,t,1e-8) です. これは, 積分許容誤差 1e-8 で, 0 からある可変量 t までのゼータの積分を定義します. substval() は, t を現在の値 \zeta に置き換え, 畳み込みを計算できるようにします.

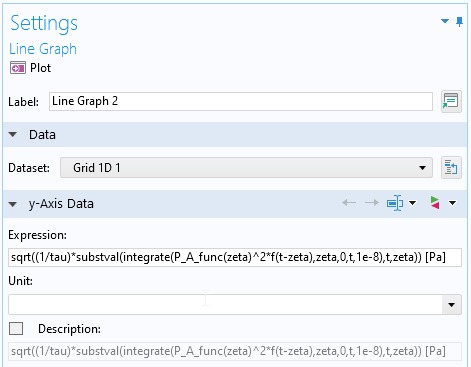
時間加重圧力の計算用の設定ウィンドウ.

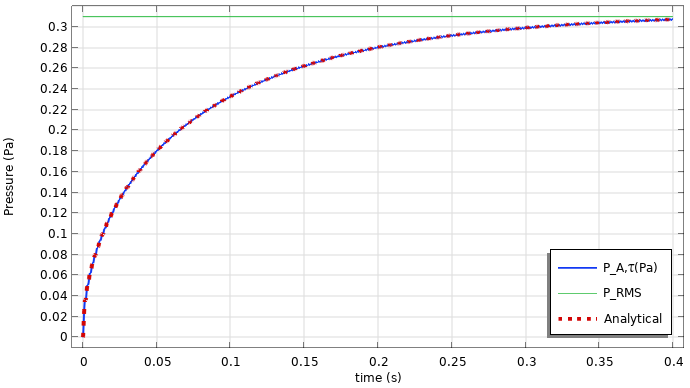
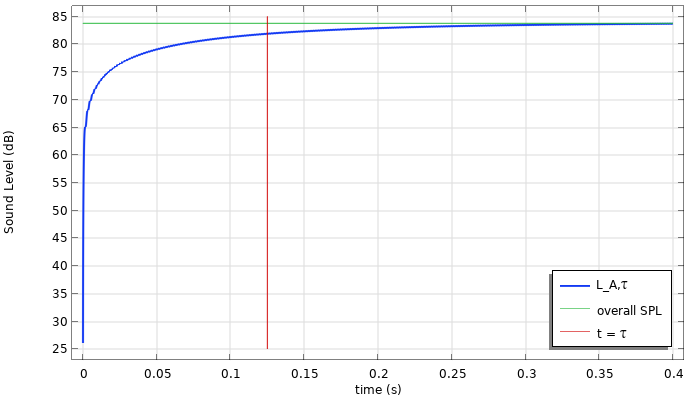
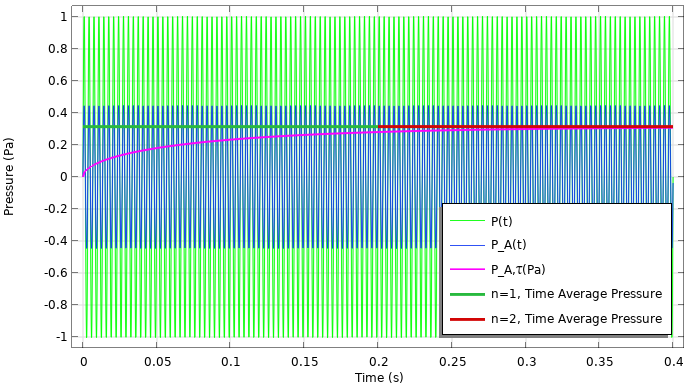
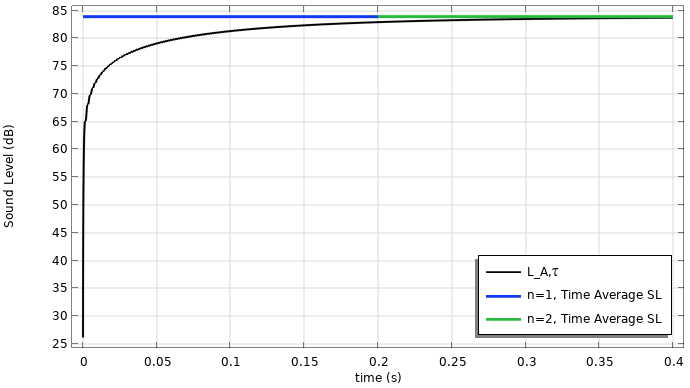
時間加重圧力と音圧レベルの結果を以下に示します. 積分が正確であるためには, 信号を時間で分解する必要があることに注意してください. 波形が純粋な正弦波の場合, いくつか興味深いことが起こる可能性があります. まず, 時間が経つにつれて, 高速加重圧力レベルと高速加重音圧レベルがそれぞれ RMS レベルと全体の音圧レベルに近づいています. 純粋な正弦波の場合, 結果は, 部分積分(複数回)を使用して導出できる畳み込み積分の解析解と照合できます. A 加重圧力振幅が P_{0A} の場合, 解析解は

です.

さらに, 時定数は, 同等レベルの約 63% に達するのにかかる時間として解釈することもできます. たとえば, 63% を dB で表すと, 10 \log_{10}{63/100} = -2dB になります. したがって, t=\tau では, 時間加重音響レベルは等価レベルより約 2 dB 低くなります (この場合は約 84～82 dB).

結果のプロットは, 時間加重圧力 (左) と音響レベル (右) です.

時間平均化

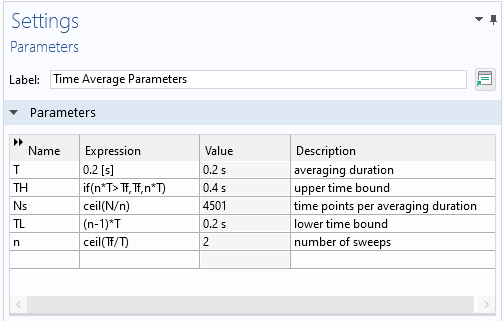
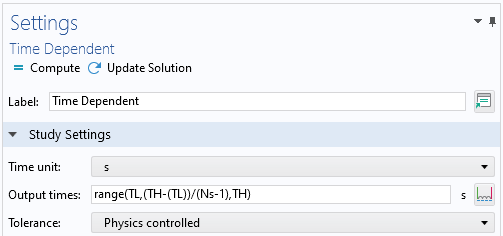
最後のステップは, 時間平均音響レベルを計算することです. 平均化期間, 平均数, 積分のための移動上限と移動下限などのパラメーターを定義します. 平均数に対するパラメトリックスイープを備えた新しい時間依存スタディが追加されました. このパラメトリックスタディの目的は, 後処理に使用できる移動上限と移動下限を作成することです. ここではフィジックスインターフェースは実際には解決されないことに注意してください.

時間平均計算用のパラメーター (左) とスタディ (右) の設定ウィンドウ.

ラインセグメントプロットをパラメトリック解データセットと共に使用して, 時間平均をプロットできます. このプロットでは, 解パラメーターが手動に, パラメーター選択がすべてに, 時間選択が最後に変更されています. 線分は, 下の時間 (x 座標) から上の時間 (y 座標) まで伸び, 式 (y 座標) は, 時間平均圧力 P_{AT} の計算であり, timeint() 演算子を使用しています.

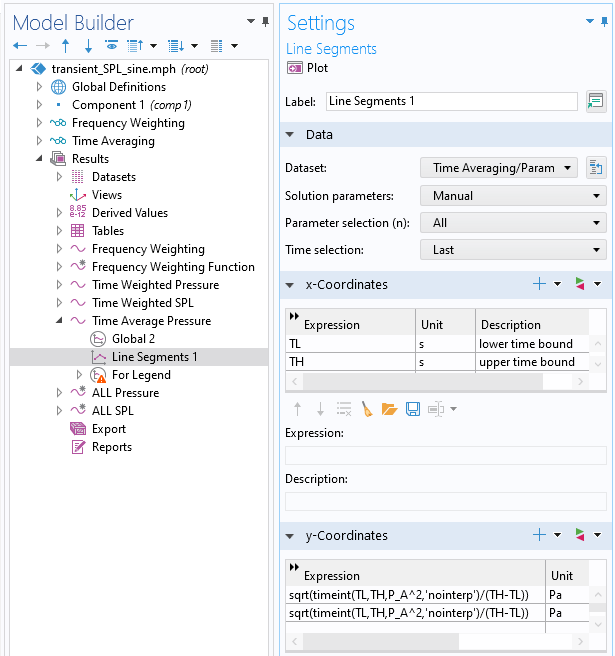
時間平均圧力をプロットするためのラインセグメントの設定ウィンドウ.

この場合, 平均時間は周期よりもはるかに長いため, 時間平均圧力は RMS 圧力です. 比較のためにすべての結果をまとめてプロットできます.

正弦波の圧力対時間 (左) と音圧対時間 (右) の結果.

例 2: ギアボックスからのノイズ

以前のブログでは, ギアボックスの振動とノイズをモデル化する方法について説明しました. ここで説明した方法論を使用すると, ノイズを後処理し, 追加の有用なメトリックをプロットできます. まず, 座標にある仮想マイクから時間依存の圧力を取得します:

• x = 0.75 \text{m}
• y = 0 \text{m}
• z = 0 \text{m}

このデータは, 補間関数に読み込まれ, 保存されます. メトリックは, 正弦検証の例と同じ方法で計算されます.

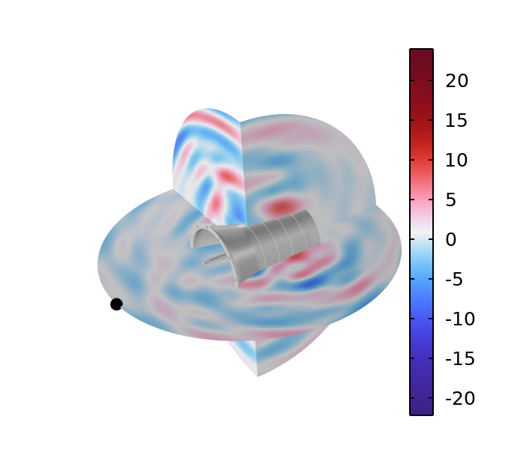
ダイナミックギアボックス周辺の音響圧力場. 時間 = 0.0020735 秒.

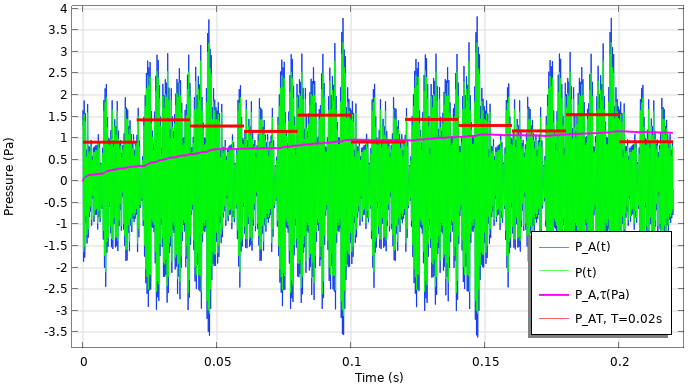
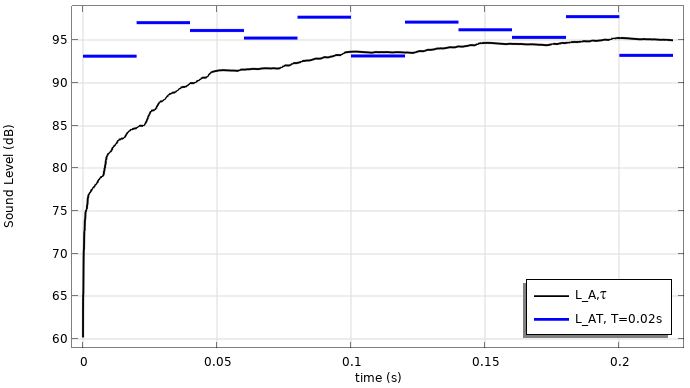
この例では, 高速加重定数 \tau = 0.125s を使用します. 平均化期間は T = 0.02s です. 結果は, A 加重圧力が元の信号と比較して増幅されていることを示しています. これは, 音響エネルギーのほとんどが 1000～3000 \text{Hz} の周波数範囲にあるためです.

ギアボックスノイズの圧力対時間 (左) と音圧対時間 (右) の結果.

ここに示す結果は, A 加重, 時間加重, および時間平均の圧力と音圧レベルです. これらのメトリックは, たとえば, 過渡シミュレーションの結果を対数スケールで解釈しやすくする場合, 結果を騒音計の測定値と比較する場合, または過渡信号が人間の耳にどのように聞こえるかに関心がある場合に役立ちます.

自分で試す

ここでは, 周波数加重, 時間加重, および時間平均を含むさまざまな過渡音響メトリックを計算する方法を示しました. ここで概説した定義と主な後処理手順は, あらゆる過渡音響シミュレーションに使用できます. 以下のボタンをクリックして, アプリケーションギャラリのエントリに移動して, 実際に試してみてください.

参考文献

1. E.H. Berger, The Noise Manual, AIHA, 2003.