
以前のブログでは, 自由表面のモデリングにフィールドベースの方法 (レベルセットとフェーズフィールド) を使用する方法について説明しました. 別のオプションである移動メッシュは, トポロジの変化を受けない自由液体表面を処理できます. このブログでは, 自由表面のモデリングに移動メッシュ法を使用する方法を示し, その結果をフィールドベースの方法と比較します.
自由液体表面の問題
移動メッシュ機能を示すために, フェーズフィールド法とレベルセット法に関する以前のブログ で使用したのと同じ問題を使用します. モデルは, 小さな流路内の水に部分的に浸された固体バーです. 移動メッシュ機能は, 実際には, レベルセット法とフェーズフィールド法, および移動メッシュ法で, 小さな長方形のバーが表面上で前後に動くように指定するためにも使用されていることに注意してください.
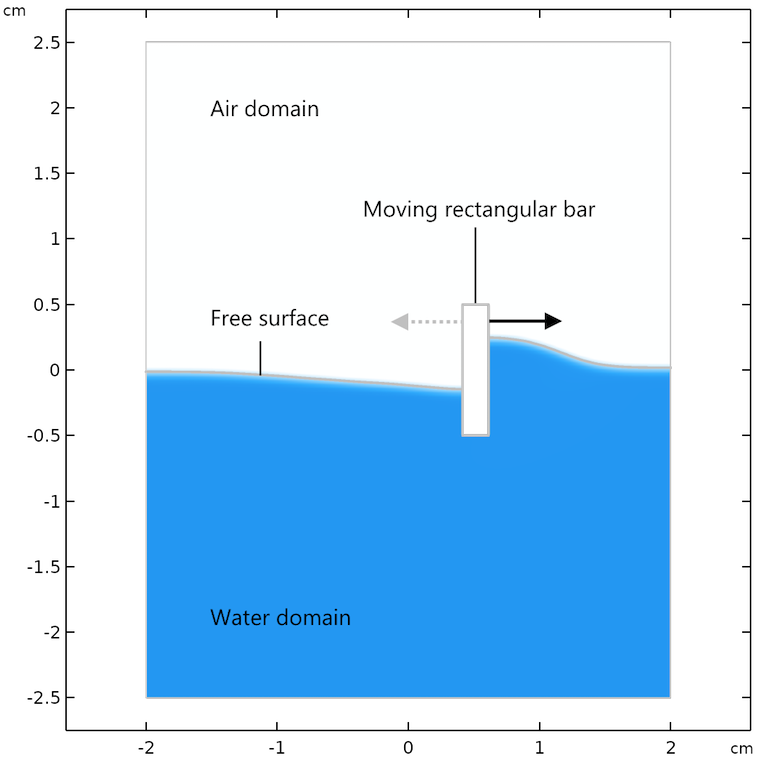
例題のジオメトリと定義.
自由表面の移動メッシュ法は長方形の棒の変位を規定し, 水面の変位を追跡します. モデル内の重力を考慮するには, 運動量方程式にソースを追加します. 移動メッシュ法の結果をフェーズフィールド法およびレベルセット法と比較するために, 壁にナビエすべり条件を使用します. スリップ長は要素の長さのサイズに等しくなります.
移動メッシュによる自由表面のモデリング
COMSOL Multiphysics® ソフトウェアの移動メッシュ自由表面モデリング機能は, 前述のレベルセット法やフェーズフィールド法とはまったく異なるアプローチで, 同じ問題に取り組みます. 移動メッシュアプローチでは, 自由表面は2つの領域を分離する幾何学的表面としてモデリングされます. 表面張力やその他の表面力は, 自由表面の境界条件として直接適用されます.
自由表面 機能を使用すると, 自由表面の変位速度は, 任意の時点での表面における流体の速度として取得されます. 移動メッシュ方程式の解は, 流体のバルク内のメッシュノードをスムーズに変位させます. ナビエ・ストークス方程式 は, 同時に解かれる移動メッシュ方程式から移動が取得される移動座標系で定式化されます.
このアプローチでは, 液体がモデル化されますが, 自由表面上のガス領域の流れ場は, 表面張力と圧力効果以外では処理されません. したがって, 現在の実装ではガス相の流れ場を取得することはできません. (もちろん, 手動で2番目の流体流れインターフェースを追加するか, マイクロフルイディクスモジュールの 2相流れ (移動メッシュ) インターフェースで使用可能な 流体間界面 機能を使用することで, これを変更できます.) さらに, COMSOL Multiphysics の移動メッシュ実装では, 波の破壊など, 自由表面のトポロジの変化を処理できません.
自由表面のモデリングは, 前述のように, 表面張力やその他の表面力を境界条件として直接適用できるため, レベルセット法やフェーズフィールド法と比較して, ある意味では移動メッシュを使用する方がクリーンです. 自由表面上の空気領域における流体の流れを解かなければ, ナビエ・ストークス系の自由度の数がフィールドベースの方法で使用される数の約半分に減るため, パフォーマンスが大幅に向上します. この場合, 空気領域の影響を無視するのは, 水と空気の密度と動粘性の比率が大きいためです. 結果の違いについては, 次のセクションで説明します.
移動メッシュとフェーズフィールドの結果の比較
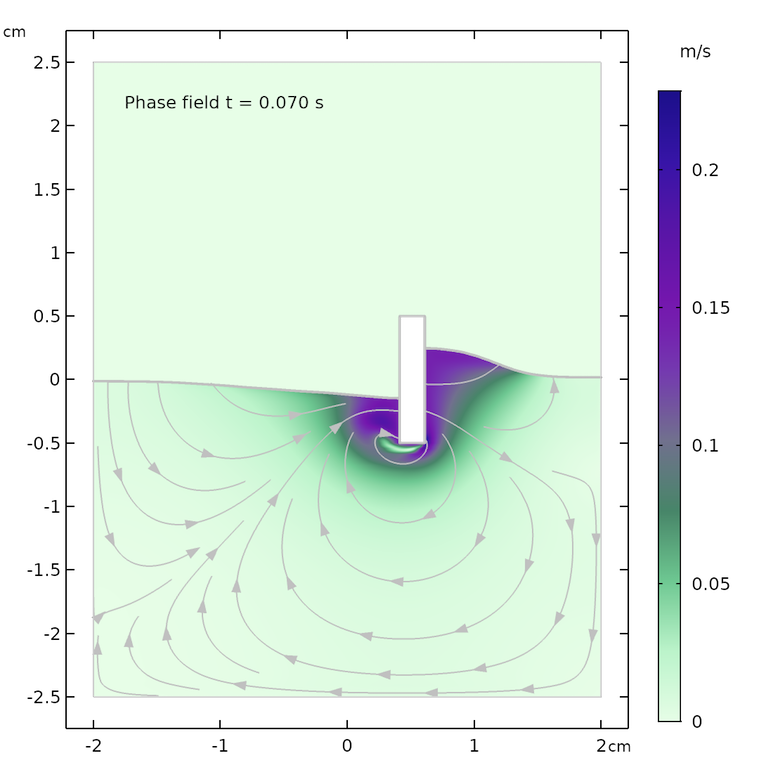
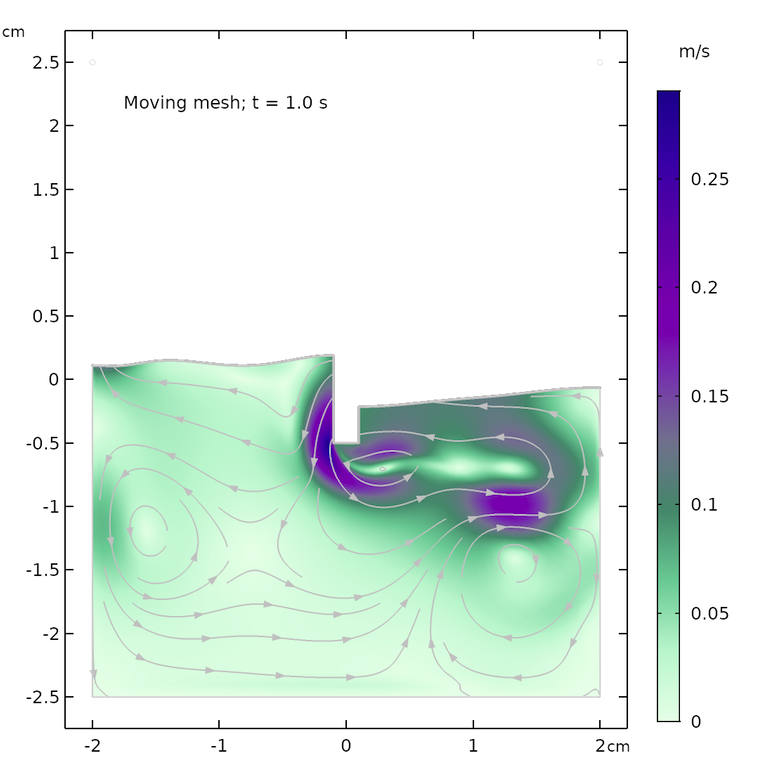
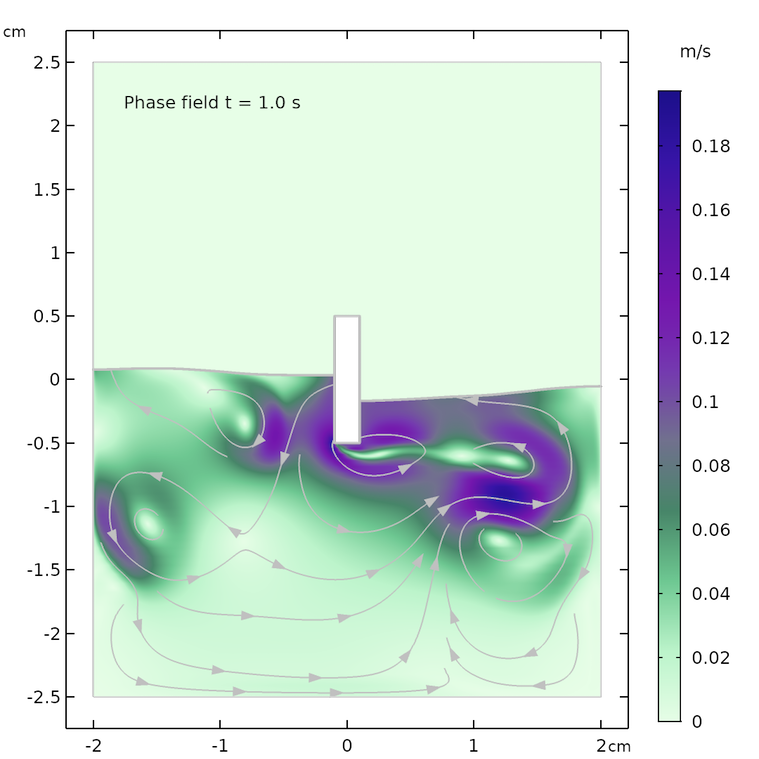
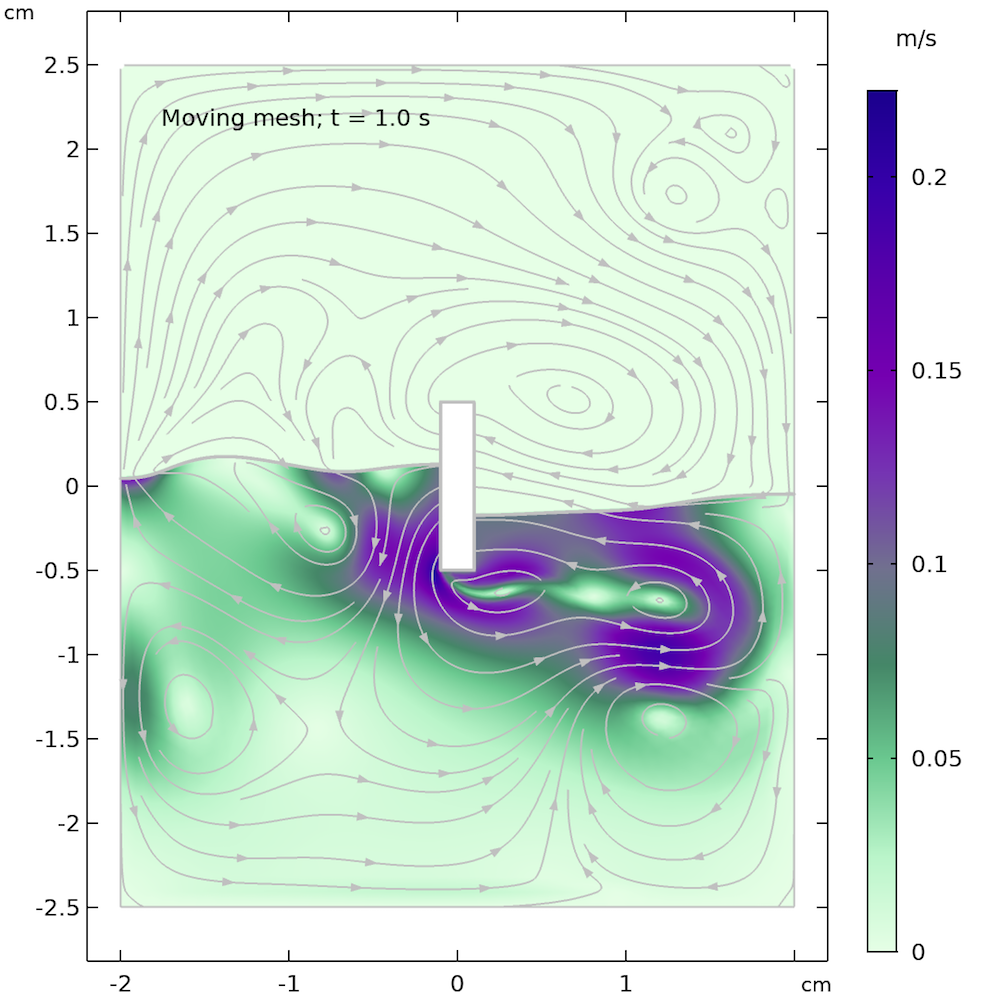
以下の図は, 移動メッシュを使用して計算された自由表面と, フェーズフィールド法を使用して計算された結果を比較したものです. 2つの方法の一致は良好で, 自由表面の形状と速度フィールドの流線はどちらも類似していることがわかります.
ただし, モデルは同一ではありません. フェーズフィールドの場合の自由表面上の空気領域は, フェーズフィールド法の表面に小さな減衰効果をもたらします. 移動メッシュの場合, 空気領域は存在せず, 表面は流体表面の上にある一定の空気圧のみを “認識” します. 言い換えれば, 可動メッシュケースの自由表面は空気を押しのける必要がなく, このエネルギーを使用してわずかに高い波とより波打った表面を作り出すことができます.
2相流の移動メッシュインターフェース (左) とフェーズフィールド法 (右) を使用して計算された, 異なる時間における自由表面の形状と速度場.
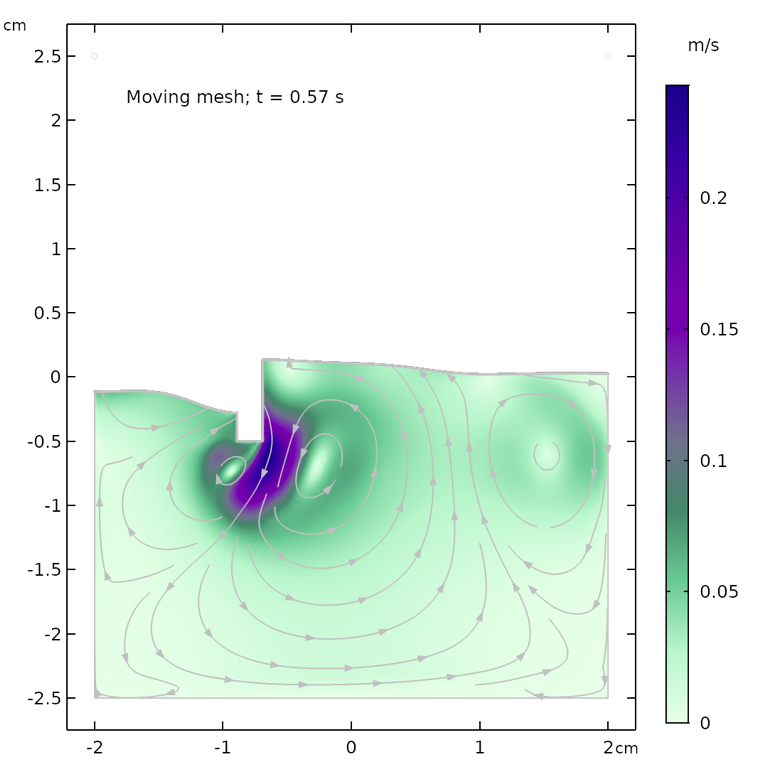
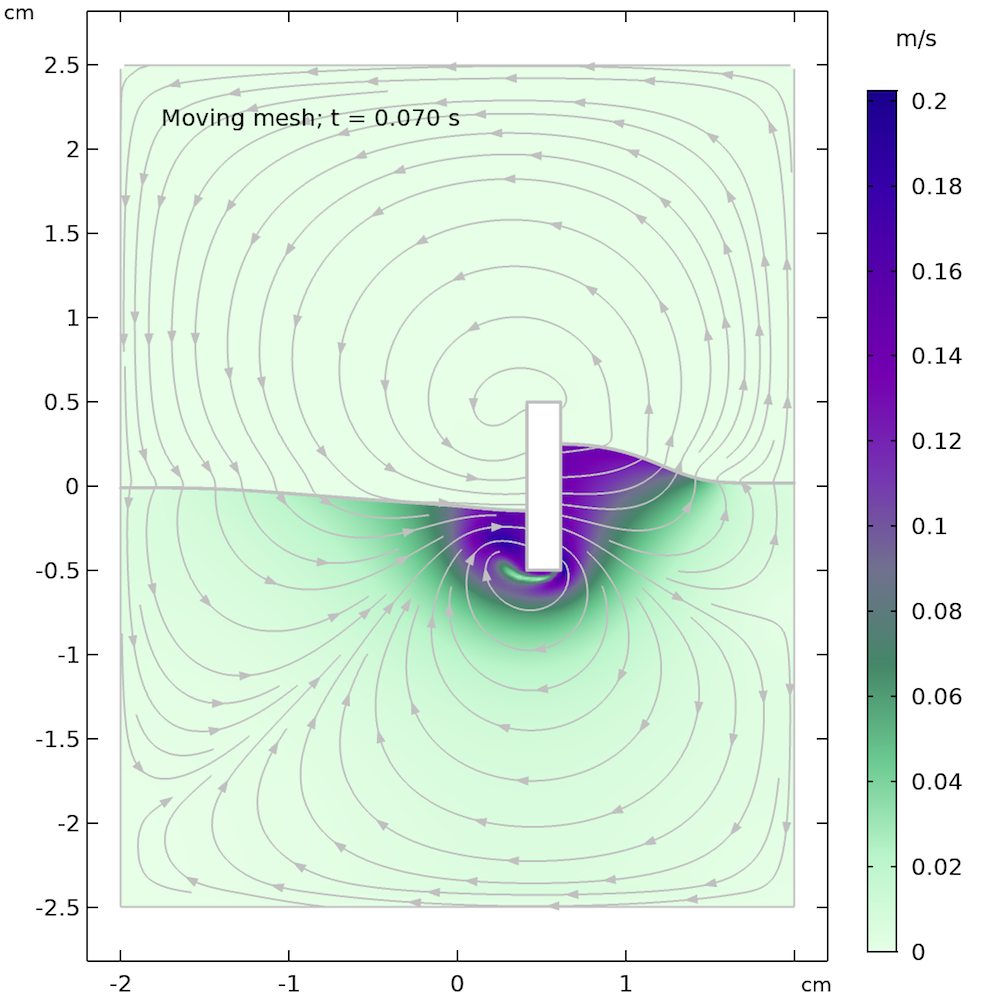
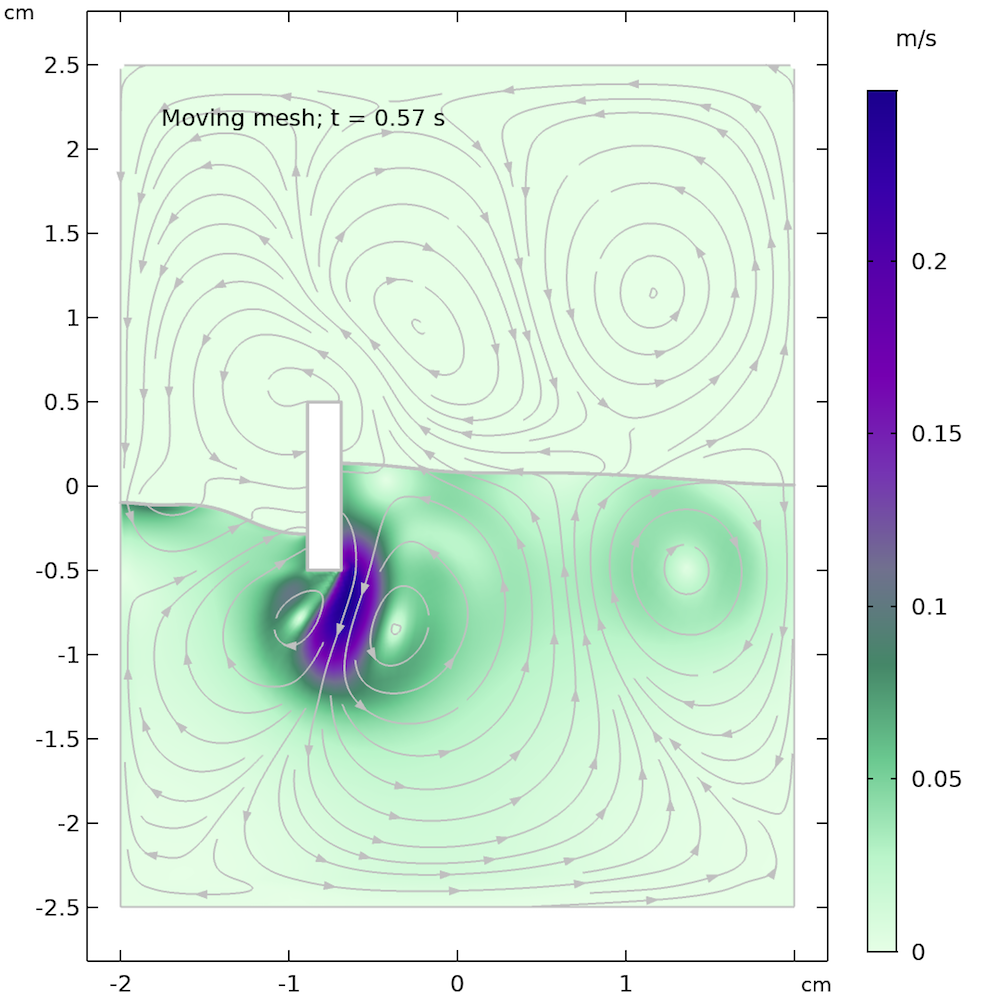
下のアニメーションは, 自由表面の移動メッシュ法による解を示しています. これは, フェーズフィールド法を使用した以前のアニメーション と比較できます. フェーズフィールドアニメーションと比較して, 自由表面がより波打っており, より速く反応していることがはっきりとわかります. これは, レベルセット法とフェーズフィールド法に存在する空気領域が, 自由表面の動きを減衰させるため, 移動メッシュに空気領域が欠落しているためである可能性があります.
自由表面の移動メッシュ法から得られたアニメーション.
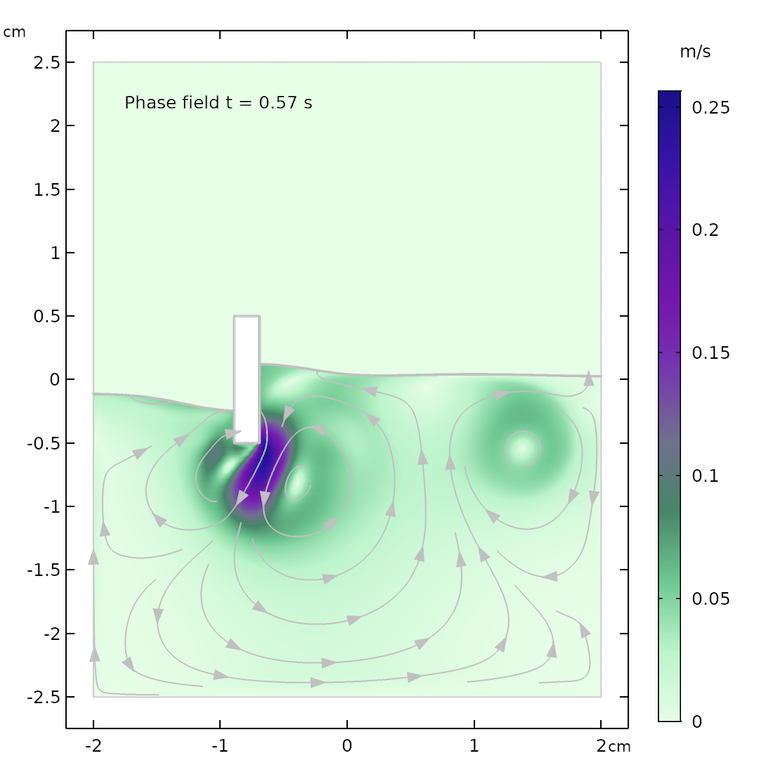
また, デフォルトの自由表面移動メッシュ機能を, 液体と気体の両方の相における流れ場を考慮できる完全な 2相流移動メッシュ インターフェースと比較することもできます. 2相の移動メッシュでは, フェーズフィールド法の結果と比較して, 流れ場のパターンと速度ベクトルの大きさが非常に似ていることがわかります. 自由表面の形状は, 3つのケース (移動メッシュ, フェーズフィールド, 2相の移動メッシュ) すべてで非常に似ていますが, ここでは2つの移動メッシュケースの形状がより似ています. シミュレーション結果によると, 空気領域は液体の速度場に対してある程度の減衰効果を持つという結論になります. さらに, 移動メッシュ法とフェーズフィールド法が相境界で壁面を処理する方法の違いが, 自由表面の形状の違い (小さいながらも) の原因であると思われます.
2相流移動メッシュインターフェースを使用した結果.
自動再メッシュと自由表面
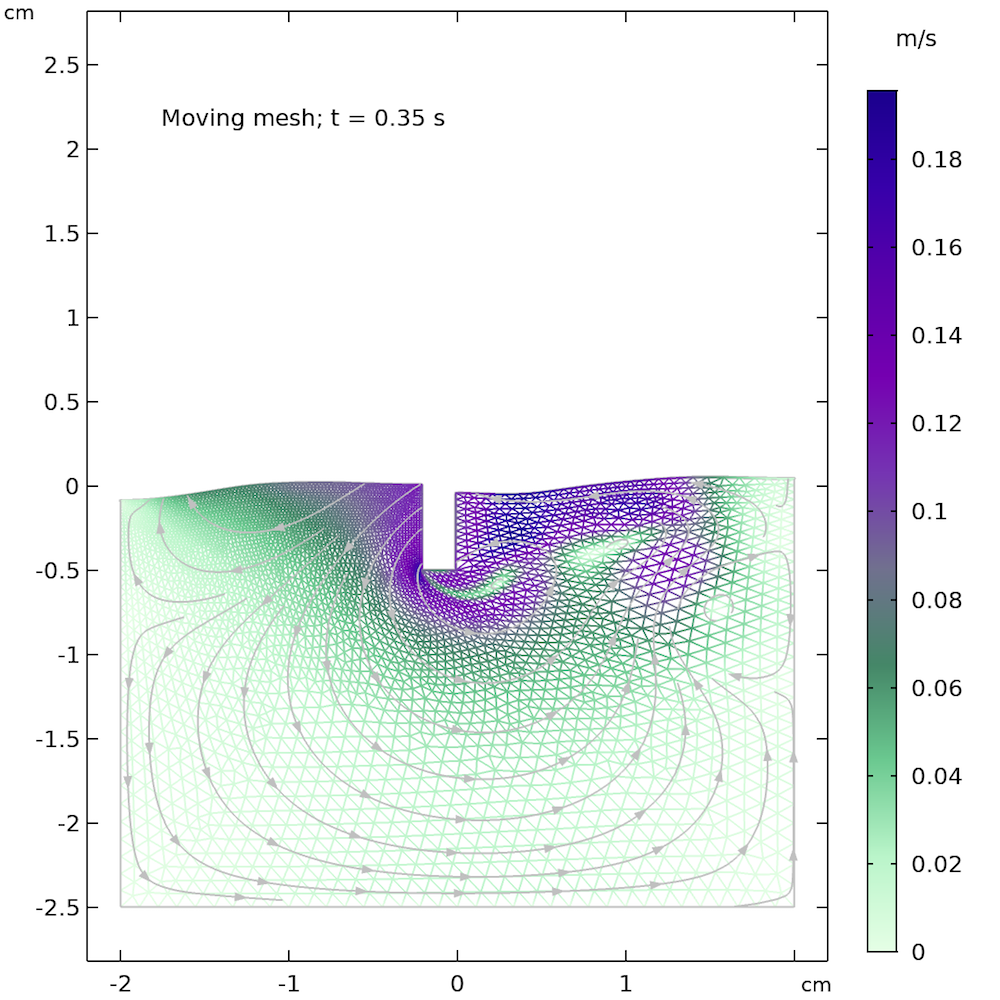
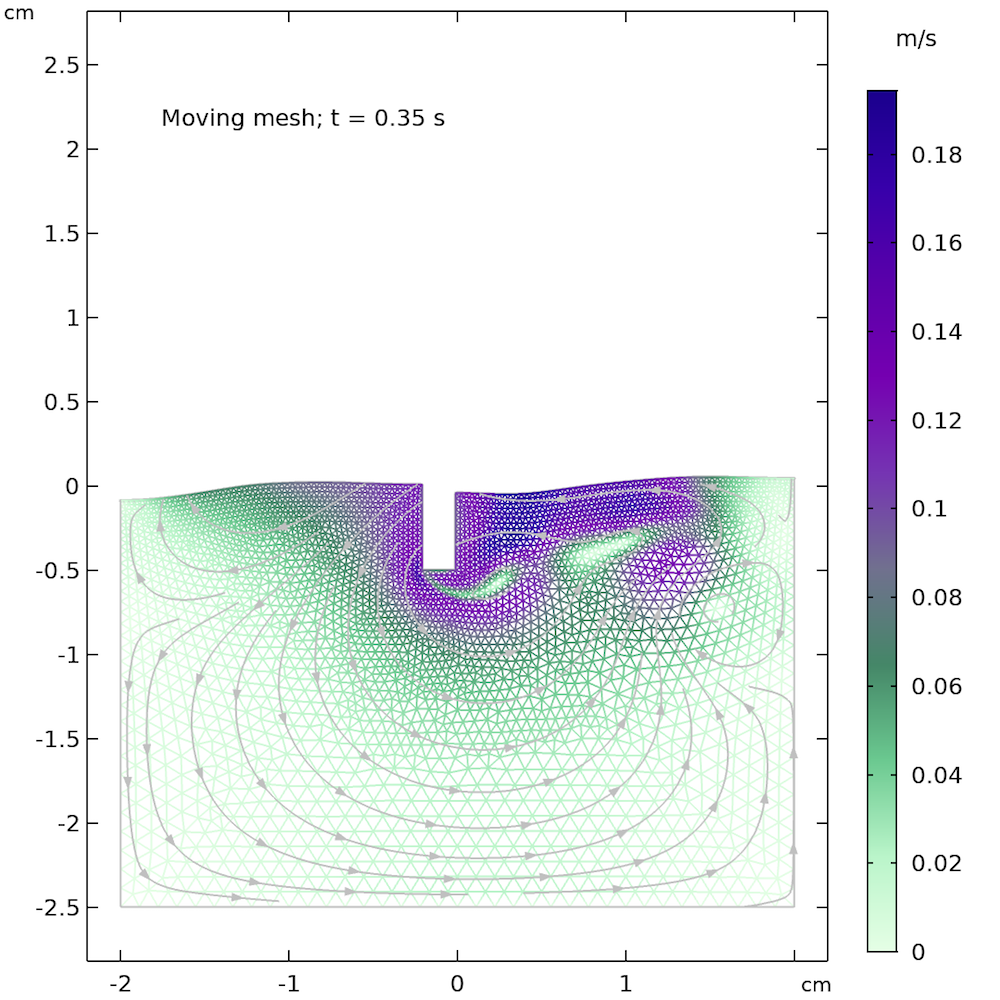
フェーズフィールド, レベルセット, 移動メッシュの各方法では, 自動再メッシュの使用も検討できます. 自動再メッシュは, 要素の品質が低すぎて必要な品質を満たせない場合に自動的に再メッシュします. 品質は, 要素の最大角度と, 最大エッジと最小エッジの関係に関係します. 角度が非常に大きい, または要素が非常に圧縮されている場合は, 要素の品質が低いことを意味し, この機能を選択すると, 自動再メッシュがトリガーされます. 下の図は, 小さなサンプル問題に適用された自動再メッシュを示しています. 0.35秒後の要素の品質は, 再メッシュをトリガーするほど低く, メッシュの品質が大幅に向上します.
再メッシュ前のメッシュ (左) と再メッシュ後 (右). 小さな長方形のバーの右側の要素は再メッシュ前は引き伸ばされていますが, 再メッシュ後はより等方性に見えます.
流体構造相互作用と自由表面
例題では, 表面上の小さな長方形のバーの変位を指定します. バーに力を適用し, 流体によって適用される反力によるバーの変位を実際に計算することで, 問題を拡張するのは非常に簡単です. これにより, いわゆる流体構造相互作用 (FSI) 問題が生まれます.
COMSOL Multiphysics バージョン 5.3a では, 新しい流体構造相互作用インターフェースの導入により, FSI を使用した自由表面問題 (または2相流問題) の定義が容易になりました. 下の図は, 流体壁が崩壊する古典的な問題を示していますが, その途中で小さな障害物にもぶつかっています. 表面張力, 液体界面の位置, 流れの影響は, 流れに当たった小さなウィスカーの構造変位と応力およびひずみと完全に連動しています.
流入する水脈に当たったウィスカーの2相流 FSI 問題のアニメーション. 長さスケールは深さ 5 mm です.
例題からのいくつかの結論
このブログシリーズのパート1では, 表面張力の影響が存在する系の自由表面をモデル化する場合に, フェーズフィールド法がレベルセット法よりもパフォーマンスと精度の点で優れているという結論に達しました. 例題の求解法は, 自由表面機能を備えた移動メッシュ法がパフォーマンスと精度の点でさらに優れていることを示しています. ただし, 2つの欠点があります:
- トポロジの変化を処理できない.
- デフォルトでは, 自由液体表面の上の空気 (またはその他のガス) を考慮しない.
トポロジの変化が予測されない場合は, 移動メッシュ法が自由表面のモデリングの第一の選択肢であると結論付けることができます. 表面張力とトポロジの変化がある場合は, フェーズフィールド法が最適な選択肢です. おそらく, 今後のブログで, トポロジの変化の有無にかかわらず表面張力の影響が無視できる問題に対して, これら3つの方法を比較できるでしょう.
その他の資料
前述の レベルセット法とフェーズフィールド法に関するブログ をお読みください.
上記の例はすべて, アプリケーションギャラリで入手できます. 必要に応じて, 結果を再現して有効性を確認できます. このシリーズで紹介されているモデルにアクセスし, 自由表面のモデリングについてさらに詳しくお読みください:




コメント (0)